平面圖的多項式與著色
韓友發, 亢云鳳, 董 婷
(遼寧師范大學 數學學院, 遼寧 大連 116029)
平面圖的多項式與著色
韓友發, 亢云鳳, 董 婷
(遼寧師范大學 數學學院, 遼寧 大連 116029)
研究平面剖分圖的著色性質,通過討論圖的色多項式的零點問題,分析對圖的著色保證相鄰的兩個區域著不同顏色的最少方法數目,進而給出了平面剖分圖的著色方法數目的重要性質.主要研究方法是對平面圖的著色提供了一個新的研究渠道,即通過色多項式計算,得出平面剖分前后的著色數目,進而再計算球面剖分圖的著色數目.首先,研究“具有一條公共邊的兩個區域Gn和Gm,及廣義剖分圖”的著色問題;其次,研究“簡單正多面體及球面的三角剖分圖”的著色問題.
平面圖;色多項式;廣義剖分;三角剖分
紐結理論是20世紀以來作為拓撲學的一個重要部分而發展起來的.而且在很多領域得到了應用,進而紐結理論成了拓撲學中引人入勝的一支,它在數學中的重要性日漸上升.1928年由美國數學家亞歷山大[1]發現了亞歷山大多項式,但是該多項式不能區分紐結和它的鏡面像,也就是它們相同的亞歷山大多項式.經過50多年,1984年新西蘭數學家瓊斯[2]找到紐結新的一個多項式不變量能夠區分某些亞歷山大多項式不能區分的紐結.很快,許多科學家發現紐結理論和許多科學領域都有聯系,數學家考夫曼[3]試圖用圖式方法來探究紐結不變量,而且發現紐結理論與圖論有密切的聯系,即紐結的投影圖與平面圖是一一對應的.進而在圖論上來探究紐結的交叉點的符號問題,這樣就涉及在平面圖上的著色問題.平面圖的著色問題的研究來源于圖論中的著色理論.塔特多項式和方括號多項式是紐結理論和圖論的基本關系的主要橋梁,尤其是塔特多項式及與色多項式之間的關系[4-5]對著色問題的研究具有重大的意義.同時,紐結理論在統計力學、生物DNA分子重組等領域都有著廣泛的應用[6-8].筆者就是在分析研究這些成果的基礎上,重點研究圖及剖分圖的著色問題.
1 預備知識
1.1 圖論中的一些定義
定義1.1一個圖是一個偶對V,E:
(1)V是一個集合,其中的元素稱為頂點.
(2)E是無序積V×V中的一個子集合,其中的元素稱為邊;集合V×V中的元素可在E中出現不止一次.
定義1.2起點和終點相同的路徑稱為閉路徑,閉路又稱為圈.長為k(k即是邊長的個數)的圈稱為k-圈,k為偶數時稱為偶圈,k為奇數時,稱為奇圈.
定義1.3圖G稱為多重圖,如果G中有兩個頂點之間有多重邊或有一個頂點帶一個環.
定義1.4平面圖G的對偶圖G*定義如下:G中每一個面f內取一點作G*的一個頂點f*,G*中的f*、g*相連接e*的充要條件是f*,g*在G中對應的面f,g含公共邊e,且使e和e*相交.
定義1.5平面圖G的k-面著色是k種顏色在G的面上的一個分配,稱面著色的平面圖為k-面可著色.使G為k-面可著色的最小的k稱為G的面色數,記為x*G.顯然,對任意平面圖G,都有x*G=xG*.
1.2 圖的雙色多項式
首先介紹圖的雙色多項式Z(G)[3],它有兩個變量q和v,滿足下面3個條件:
(1)Z(?)=q;

例
(1)Z()=Z(?)+vZ(?)=q+vq;

P(G)有下列性質:
引理1.1[5]在雙色多項式Z(q,v)中,當v=-1時,雙色多項式特殊化為色多項式P(G).P(G)表示對圖G的頂點用q種顏色著色并保證相鄰的兩個頂點不同色的著色的方法數目.
引理1.2[5]如果圖G是子圖H和K的不交并,那么P(G)=P(H)P(K).
引理1.3[5]如果圖G是子圖H和K的并,滿足H∩K是一個頂點,那么
qP(G)=P(H)P(K).
1.3 廣義剖分和三角剖分
定義1.6對于一個單純復形K,找到其重心O,把重心O與單形的相應的頂點連接起來的一種剖分,稱這種剖分為廣義剖分.重復上述過程k次得到的圖記為TkK(k≥1).
例單形K的一次廣義剖分.
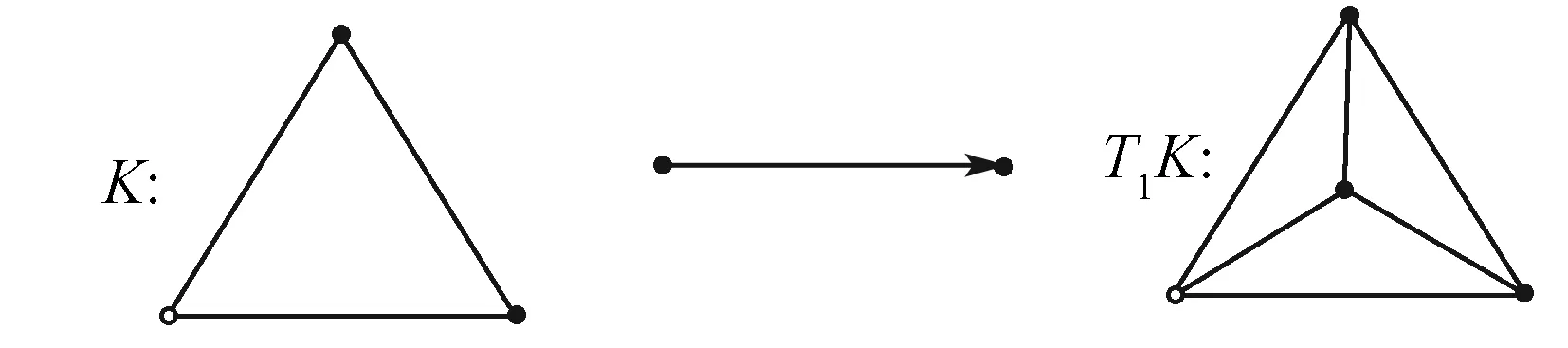
定義1.7拓撲空間X稱為多面體,如果存在單純復形K與同胚f:|K|?X.這時把單純復形K與同胚f組成的對偶(K,f)稱為空間的一個三角剖分.
2 討論圖和剖分圖的著色數目
對圖剖分后區域著色問題進行研究,即計算圖的廣義剖分及三角剖分后的色多項式來進一步觀察剖分后圖的著色數目,看一看剖分前后圖的著色數目是否有變化,通過前后圖形的著色數目的對比進行一些題目的討論并得到一些結論.為了便于計算把區域圖G轉化為其頂點的對偶圖G*來研究.
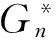
(1)當n是奇數時,如果q≥3,則P(G*)≠0.
(2)當n是偶數時,如果q≥2,則P(G*)≠0.

圖1 Gn與其對偶圖Fig.1 Gn and its dual graph
注這說明n個區域圖的著色情況為:當區域數為偶數時,可以用兩種或兩種以上的顏色著色就可以保證相鄰區域著不同的顏色;而當區域數為奇數時,可以用3種或3種以上的顏色著色可以保證相鄰區域著不同的顏色.
定理2.1設G(見圖2)是由Gn和Gm構成,且Gn和Gm有一條公共邊,則有
(1)當n與m中有一個為奇數,且q≥3時,P(G*)≠0.
(2)當n與m都為偶數,且q≥2時,P(G*)≠0.
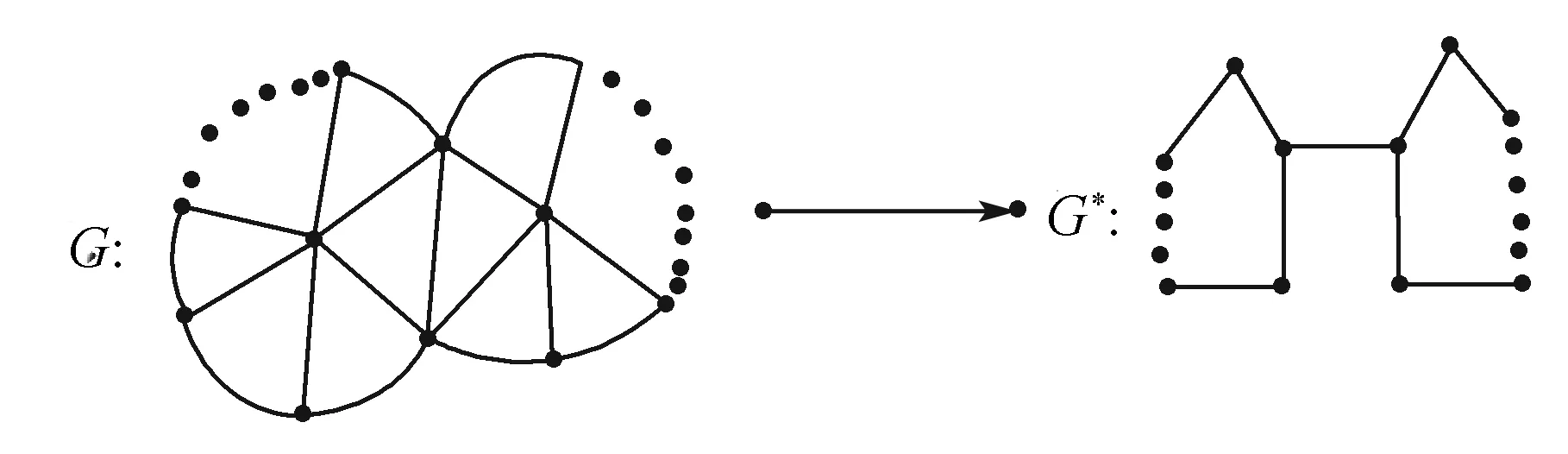
圖2 有一個公共邊的平面圖和其對偶圖Fig.2 The plane graph with one common edge and its dual graph
證由引理1.2和引理1.3知道
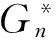

當v=-1時,有
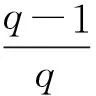
由引理2.1知:
n與m中有一個為奇數時,且當q≥3時,P(G*)≠0.
n與m都為偶數時,且當q≥2時,P(G*)≠0.
因此定理得證.
定理2.2設圖G(見圖2)是由Gn和Gm構成,且Gn和Gm有一條公共邊,對G進行一次廣義剖分后圖T1G(見圖3),則有:當q≥3時,P(T1G*)≠0.
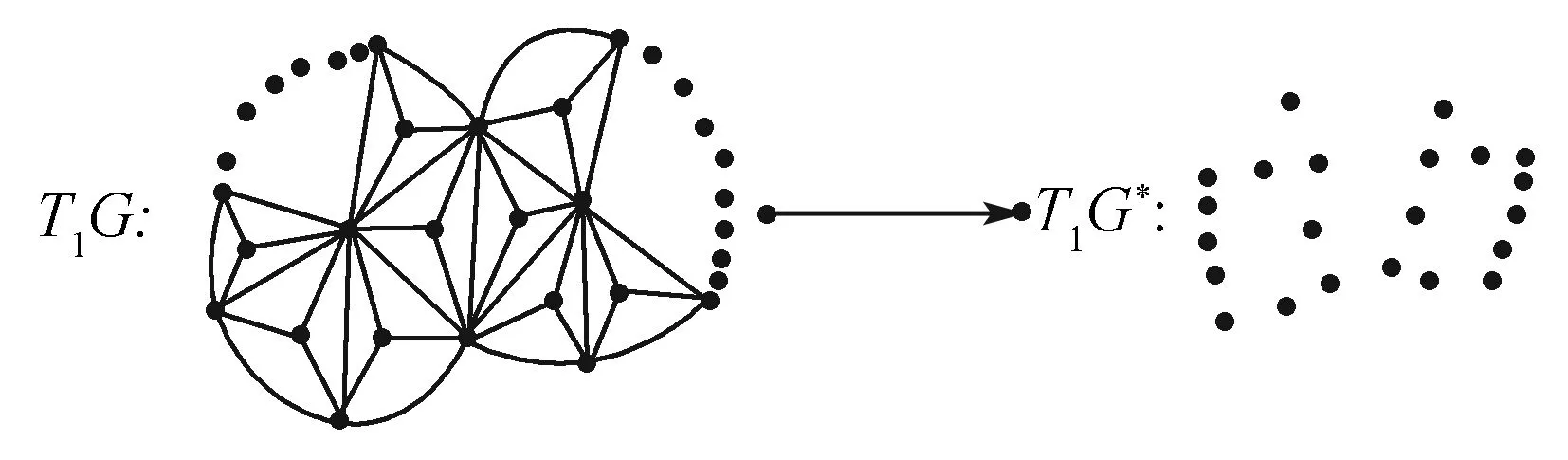
圖3 廣義剖分的平面圖Fig.3 Generalized division plane graph
證由引理1.2與引理1.3有
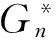
令v=-1時,有
注1定理說明有一個公共邊的兩個圓盤區域經一次廣義剖分后可以用3種或3種以上的顏色著色能保證相鄰區域著不同的顏色.給出了研究平面圖著色的一種方法.
注2應用本文的方法可以討論多面體及球面的三角剖分圖的著色數目的性質.
[1] ALEXANDER J W.Topological invariants of knots and links[J].Trans Amer Math Soci,1928,30(2):275-306.
[2] JONES V F R.Hecke algebra representations of braid groups and link polynomials[J].Annals of Maths,1987,126:335-388.
[3] KAUFFMAN L H.New invariants in the theory of knots[J].The American Mathematical Monthly,1988,95(3):195-242.
[4] BOLLOBA B.Modern graph theory[M].Berlin:Springer,1998:335-378.
[5] TUTTE W T.Graph theory[M].Addison-Wesley, Reading, MA, 1969:253-284.
[6] BAXTER R J.q colorings of the triangular lattice[J].J Phys A:Math Gen,1986,19:2821-2839.
[7] ERNST C,SUMMERS D W.A calculus for rational tangles:applications to DNA recombination[J].Math Proc Camb Phil Soc,1990,108:489-515.
[8] ERNST C,SUMNERS D W.Solving tangles equations arising in a DNA recombination model[J].Math Proc Camb Phil Soc,1999,126:23-36.
[9] 韓友發,王英姣,沙欣,等.某些平面圖著色的性質[J].吉林師范大學學報(自然科學版),2016,37(1):36-40.
PolynomialofcoloringtheGraph
HANYoufa,KANGYunfeng,DONGTing
(School of Mathematics, Liaoning Normal University, Dalian 116029, China)
In this paper, we study properties of division plane graph with coloring by discussing the zeros of chromatic polynomial of graphs. We analyze the minimum number of ways to faces by coloring the graph, so that no two adjacent faces receive the same color, giving the important properties of the number of ways to color plane division figure. This paper gives a new study method of coloring plane division figure.We compute the dichromatic polynomial of graphs, summarize the coloring properties of decomposing plane before and after,and discuss the coloring properties of sphere division figure.We discuss the coloring number of the regional figureGnandGmwith a public side and their generalized division figure, and also discuss the coloring number of the triangulation figure of simple polyhedron and sphere.
plane graph;chromatic polynomial;generalized division;triangulation
O189.3
:A
2017-04-05
國家自然科學基金資助項目(11471151)
韓友發(1962- ),男,吉林長春人,遼寧師范大學教授,博士.
1000-1735(2017)03-0289-04
10.11679/lsxblk2017030289

