“圓”來如此
——透視220011777年中考題

駱麗葉

“圓”來如此
——透視220011777年中考題

駱麗葉

圓這一章所涉及的知識點多，且綜合性較強，同學們在學習這一章時會遇到一些困難.下面我們結合2017年中考題和大家已學內容，一起來看看圓有哪些?？嫉膬热莅?

考點一：圓周角

例1（2017·揚州）如圖1，已知⊙O是△ABC的外接圓，連接AO，若∠B=40°，則∠OAC=_______°.

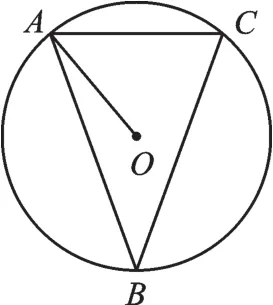
圖1

【分析】如圖2，連接OC，根據圓周角定理求出∠AOC的度數，再根據同圓的半徑相等，進而求出∠OAC的度數.

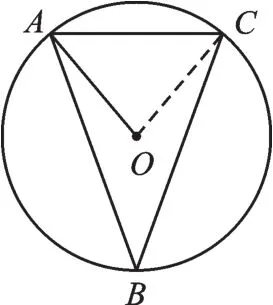
圖2

解：如圖2，連接CO.

∵∠B=40°，∴∠AOC=2∠B=80°，

又∵AO=CO，

∴∠OAC=∠OCA=（180°-80°）÷2=50°.

【點評】求圓中角度的問題，若已知圓周角，可找該圓周角所對的弧，再找該弧所對的圓心角.更多計算還可以根據三角形的內外角關系，或內角和定理，或借助等腰三角形（圓的半徑相等，可構造等腰三角形），或直角三角形（直徑所對圓周角為直角）的性質等來計算.

考點二：垂徑定理

例2（2017·黔東南州）如圖3，⊙O的直徑AB垂直于弦CD，垂足為E，∠A=15°，半徑為2，則弦CD的長為（）.

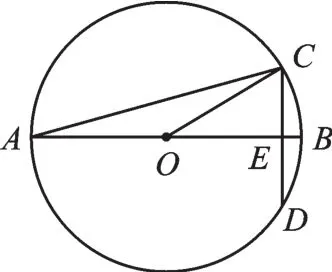
圖3

A.2B.-1C.2D.4

【分析】根據垂徑定理得到CE=DE，∠CEO=90°，根據圓周角定理得到∠COE=30°，根據直角三角形的性質得到，得出結論.

解：∵⊙O的直徑AB垂直于弦CD，

∴CE=DE，∠CEO=90°，∵∠A=15°，∴∠COE=30°，

∴CE=OC=1，

∴CD=2CE=2.

故選A.

【點評】運用垂徑定理求相關線段的長度，關鍵是構造直角三角形，利用勾股定理或者30°特殊角求解.

考點三：切線的性質與判定

【分析】（1）如圖7，連接OB，由垂徑定理的推論得OE⊥BD，弦被平分，弧被平分，由圓周角定理得出∠BOE=∠A，證出∠OBC=90°即可；（2）由勾股定理求出OC，再由△OBC的面積求出BE，即可得出弦BD的長.

例3（2017·連云港）如圖4，線段AB與⊙O相切于點B，線段AO與⊙O相交于點C，AB=12，AC=8，則⊙O的半徑長為_______.

圖4

【分析】如圖5，連接OB，根據切線的性質可知OB⊥AB，可設圓的半徑為r，根據勾股定理即可求出半徑長.

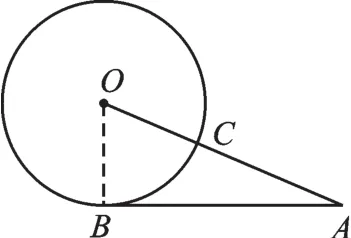
圖5

解：如圖5，連接OB，設半徑為r.

∵線段AB與⊙O相切于點B，∴OB⊥AB，∴r2+AB2=（r+AC）2，即r2+122=（r+8）2，解得r=5.

【點評】根據切線的性質求線段長度的問題，一般先找到直角三角形，再利用勾股定理使問題得以解決.

例4（2017·天水）如圖6，△ABD是⊙O的內接三角形，E是弦BD的中點，點C是⊙O外一點且∠DBC=∠A，連接OE延長與圓相交于點F，與BC相交于點C.

（1）求證：BC是⊙O的切線；

（2）若⊙O的半徑為6，BC=8，求弦BD的長.

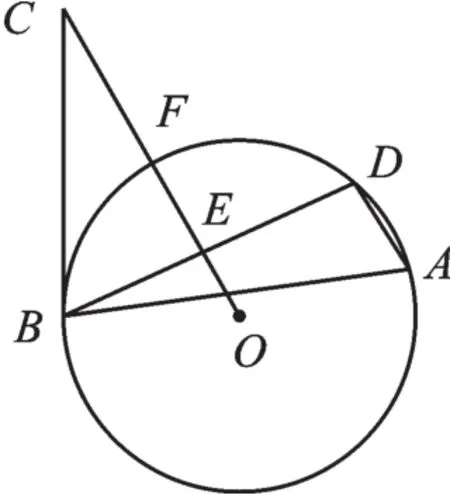
圖6

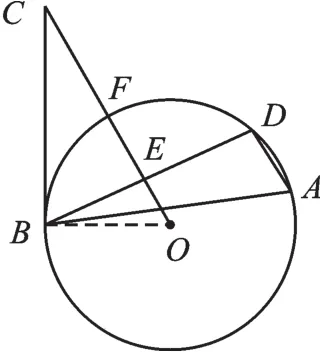
圖7

（1）證明：如圖7，連接OB.

∵E是弦BD的中點，

∴BE=DE，OE⊥BD，

∴∠BOE=∠A，∠OBE+∠BOE=90°，

∵∠DBC=∠A，

∴∠BOE=∠DBC，

∴∠OBE+∠DBC=90°，

∴∠OBC=90°，即BC⊥OB，

∴BC是⊙O的切線.

（2）解：∵OB=6，BC=8，BC⊥OB，

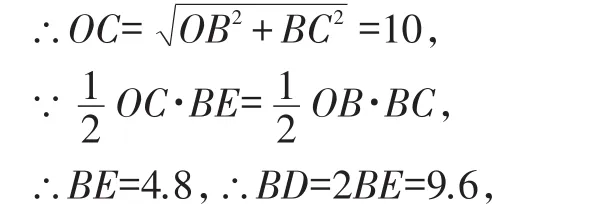
即弦BD的長為9.6.

【點評】證明切線的常用方法有兩種：①連接過這點的半徑，證明半徑與這條直線垂直，問題（1）就是用這個方法；②過圓心做直線的垂線段，證明垂線段長等于圓的半徑.問題（2）中，我們要知道若弦被直徑平分，求該弦長度時一般是先求其一半，可通過直角三角形求解.

考點四：三角形與內切圓、外接圓

例5（2017·眉山）如圖8，在△ABC中，∠A=66°，點I是內心，則∠BIC的大小為（）.

A.114°B.122°C.123°D.132°

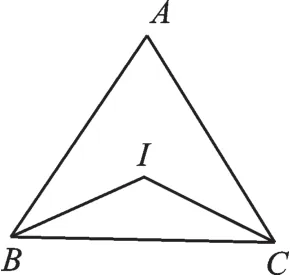
圖8

【分析】根據三角形內角和定理求出∠ABC +∠ACB，由內心的概念得∠IBC=∠ABC，

∠ICB=∠ACB，即可求出∠BIC的度數.

解：∵∠A=66°，∴∠ABC+∠ACB=114°，

∵點I是內心，

∴∠IBC=∠ABC，∠ICB=∠ACB，

∴∠IBC+∠ICB=57°，

∴∠BIC=180°-57°=123°.

故選：C.

【點評】此題考查了三角形的內切圓內心問題，解決這類問題的關鍵是理解內心的概念，再結合三角形的內角和即可完成.

考點五：圓錐的相關計算

例6（2017·大慶）圓錐的底面半徑為1，它的側面展開圖的圓心角為180°，則這個圓錐的側面積為_______.

【分析】利用公式先求出母線長，再求圓錐的側面積.

【點評】有關圓錐的計算問題，關鍵是理解圓錐的側面展開圖是扇形，其中圓錐的母線長為扇形的半徑，圓錐底面圓的周長為扇形的弧長，然后利用公式計算.

考點六：陰影部分面積的計算

例7（2017·臨沂）如圖9，AB是⊙O的直徑，BT是⊙O的切線，若∠ATB=45°，AB=2，則陰影部分的面積是（）.

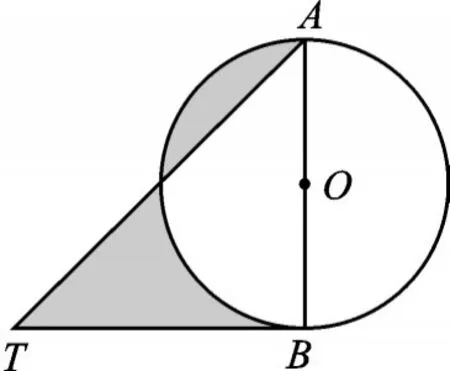
圖9

【分析】如圖10，連接BD，弓形AD的面積等于弓形BD的面積，△DTB的面積即為陰影部分的面積.

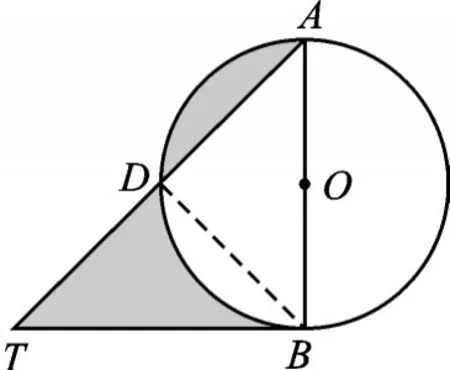
圖10

解：設AT交⊙O于D，連接BD.

∵BT是⊙O的切線，AB是⊙O的直徑，

∴∠ADB=90°，而∠ATB=45°，

∴△ADB、△BDT都是等腰直角三角形，

∴AD=BD=TD=2，

∴弓形AD的面積等于弓形BD的面積，

S陰=S△DTB=1.

故選：C.

【點評】求陰影部分面積，如不能直接用公式求解時，可將所求面積分割，利用旋轉將部分陰影圖形移位后，利用規則圖形的面積相互加減求解.

（作者單位：江蘇省連云港市海州實驗中學）