求圓周角常見錯誤分析
張靜
求圓周角常見錯誤分析
張靜
圓是初中階段重要的知識點,是中考考查重點內容之一.同學們在學習過程中感到知識點特別多,理解起來又特別難.針對弧、弦、圓心角與圓周角之間的聯系,特別在求圓周角時常會出現錯解、漏解等情況,借此文,筆者把求圓周角的易錯之處總結并歸納.
類型一:知弦求圓周角
例1在直徑為10cm的⊙O中,弦AB=5cm,則弦AB所對的圓周角為_______.
【錯解】30°.
【錯解原因】在同圓中,一條弦對著無數個圓周角,在這無數個圓周角中又可分為兩種情況,一種是圓周角的頂點在優弧上,另一種是在劣弧上.同學們在無具體圖形情況下,會習慣性地畫出弦AB向上所對的圓周角這一種情況,其實還有向下所對的圓周角,且這兩種情況的圓周角構成一個圓內接四邊形,即對角成互補關系,如圖1.
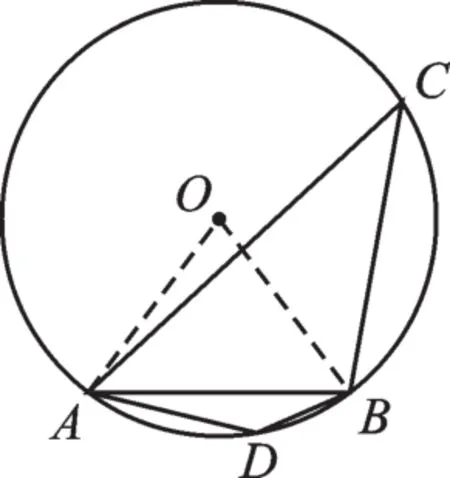
圖1
【正解】30°或150°.
解:連接OA、OB,可得△AOB是等邊三角形,即∠AOB=60°.
①當圓周角的頂點在優弧上時,則∠ACB=×60°=30°;
類型二:知圓心角求圓周角
例2如圖2,扇形OAB的圓心角為122°,C是弧AB上一點,則∠ACB=_______.

圖2
【錯解】58°.
【錯解原因】同學們以為∠ACB與∠AOB互補.出現這樣的錯誤,主要是將四邊形AOBC看成是圓內接四邊形造成的.
【正解】119°.
【解法一】設點D是優弧AB上的一點,連接DA、DB,根據同弧所對的圓周角是圓心角的一半可求得∠D的度數,再根據圓內接四邊形的對角互補,即可求得∠ACB的度數.
解:如圖3,設點D是優弧AB上的一點,連接DA、DB.

圖3
∵∠AOB=122°,

∴∠ACB=180°-∠D=119°.
【解法二】如圖4.

圖4
∵∠AOB+∠1=360°,
∴∠1=360°-122°=238°,
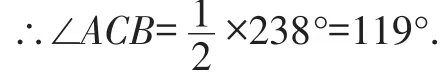
例3如圖5,量角器外緣上有A,B兩點,它們所表示的讀數分別是80°、50°,則∠ACB應為().
A.25°B.15°C.30°D.50°

圖5
【錯解】C.
【錯解原因】同學們對實際生活中的工具量角器如何量角原理理解不透,誤把量角器的讀數理解成圓周角的度數.
【正解】B.
【分析】連接OA、OB,根據量角器的讀數,可得出∠AOB的度數,再根據圓周角定理即可求出∠ACB的度數.

圖6
解:如圖6,設量角器的圓心是O,連接OA、OB,則∠AOB=80°-50°=30°,由圓周角定理得,∠ACB=15°.故選:B
類型三:知弧求圓周角
例4圓的一條弦把圓分成度數的比為1∶3的兩段弧,則弧所對的圓周角等于().
A.45°B.90°
C.135°D.45°或135°
【錯解】A或C.
【錯解原因】弧有優弧與劣弧之分,部分同學在答題時容易只考慮其中的一種,解答不全面.
【正解】D.
【分析】由圓的一條弦把圓分成1∶3的兩條弧,即可求得優弧、劣弧的度數,又由在同圓或等圓中,同弧或等弧所對的圓周角的度數等于這條弧度數的一半,即可求弧所對的圓周角的度數.
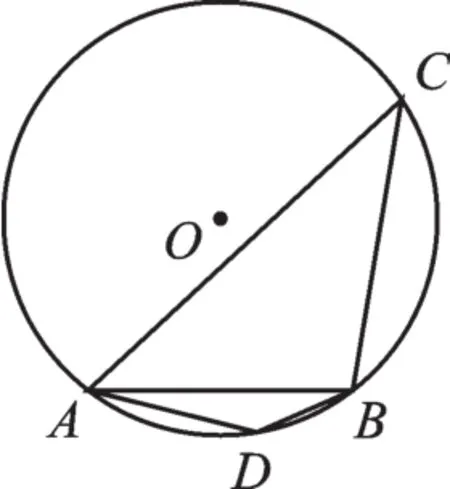
圖7
解:如圖7,∵AB把⊙O分成1∶3的兩條弧,
∴劣弧AB度數為×360°=90°,優弧AB度數為×360°=270°,
∴∠C=×90°=45°,
∠D=×270°=135°.故選:D.
(作者單位:江蘇省連云港市門河中學)

