地鐵車輛段上蓋綜合開發(fā)一體化設(shè)計(jì)
曾令福
(同濟(jì)大學(xué)建筑設(shè)計(jì)研究院(集團(tuán))有限公司,上海 200092)
1 引言
隨著城市建設(shè)的推進(jìn),軌道交通與城市的發(fā)展相互融合,一大批基于地鐵車站及地鐵車輛段場上蓋綜合開發(fā)的城市區(qū)域新中心應(yīng)運(yùn)而生。地鐵車輛段上蓋綜合開發(fā)是地鐵建設(shè)的重要組成部分,也是城市發(fā)展的良好推動力。
由于地鐵車輛段上蓋綜合開發(fā)項(xiàng)目涉及的城市功能復(fù)雜、用地權(quán)屬多樣、建設(shè)時序不一致,加之車輛段與其上蓋綜合體豎向疊加、組合建造且功能差異大,以及上蓋綜合體功能業(yè)態(tài)多變等因素,項(xiàng)目在功能布局、交通、結(jié)構(gòu)、消防、公共空間景觀等諸多方面存在設(shè)計(jì)難點(diǎn)。
本文以蘭州市軌道交通1 號線東崗車輛段上蓋綜合開發(fā)項(xiàng)目為例,結(jié)合其將上蓋綜合體與蓋下車輛段、相鄰地塊進(jìn)行一體化設(shè)計(jì)、建設(shè)的工程實(shí)踐,在系統(tǒng)闡述地鐵車輛段上蓋綜合開發(fā)一體化設(shè)計(jì)理念的基礎(chǔ)上,針對空間布局、交通規(guī)劃、結(jié)構(gòu)設(shè)計(jì)、消防設(shè)計(jì)、公共空間景觀等方面的一體化設(shè)計(jì)關(guān)鍵技術(shù)進(jìn)行分析,以期為類似項(xiàng)目提供參考和借鑒。
2 項(xiàng)目背景
蘭州市軌道交通1 號線東崗車輛段上蓋綜合開發(fā)項(xiàng)目是甘肅省第一個規(guī)劃建設(shè)且投入使用的地鐵車輛段上蓋開發(fā)項(xiàng)目,位于蘭州市城關(guān)區(qū)東部的東崗東路北側(cè),東崗車輛段運(yùn)用庫上方,與市中心東方紅廣場的直線距離約6 km;處于城市東大門的位置,是蘭州市東部城市副中心的核心組成部分。
該項(xiàng)目由車輛段上蓋開發(fā)及周邊附屬土地開發(fā)2 部分組成,形成集地鐵車輛段上蓋綜合體、相鄰白地物業(yè)、地鐵車輛段運(yùn)用庫及地鐵車站(1 號線東崗站)于一體的大型城市綜合開發(fā)片區(qū)(圖1)。其總占地面積約29.29 萬m2,建筑總面積達(dá)136 萬m2,其中地鐵車輛段運(yùn)用庫約14 萬m2,車輛段上蓋綜合體約21 萬m2,其他白地物業(yè)約101 萬m2。上蓋綜合體主體位于車輛段運(yùn)用庫頂板之上,與城市道路高差約16 m。車輛段及其上蓋綜合體總高度約40 m,其中上蓋綜合體高度約30 m。

圖1 東崗車輛段上蓋綜合開發(fā)項(xiàng)目東南側(cè)實(shí)景圖
3 一體化設(shè)計(jì)理念
東崗車輛段上蓋綜合開發(fā)項(xiàng)目自2015 年立項(xiàng)起至2021 年4 月止經(jīng)歷近6 年的規(guī)劃設(shè)計(jì)與建設(shè),目前主體已竣工并逐步投入使用。項(xiàng)目建設(shè)以一體化設(shè)計(jì)理念為指引,以打造“高效綜合社區(qū)”為目標(biāo),全面貫徹一體化設(shè)計(jì)、建設(shè)策略,通過將工作、購物、休閑、生活等城市功能進(jìn)行高度融合,形成帶動周邊區(qū)域一體化發(fā)展的核心。
(1)結(jié)合城市區(qū)域發(fā)展,總體謀劃項(xiàng)目定位。即充分發(fā)揮項(xiàng)目地處城市東大門的地理優(yōu)勢、作為東部城市副中心核心組成部分的定位優(yōu)勢、毗鄰1 號線東崗路站的交通優(yōu)勢,通過分析其所處城市區(qū)域的交通、服務(wù)、產(chǎn)業(yè)、消費(fèi)、居住等功能相關(guān)基本信息,提出打造以車輛段上蓋綜合體為核心,集居住、辦公、商務(wù)、休閑、教育等功能于一身的一體化發(fā)展綜合區(qū)(圖 2),形成車輛段開發(fā)與城市區(qū)域發(fā)展高效協(xié)同的一體化發(fā)展格局,實(shí)現(xiàn)以車輛段上蓋綜合開發(fā)帶動車輛段開發(fā)、以車輛段片區(qū)開發(fā)引領(lǐng)城市區(qū)域發(fā)展。
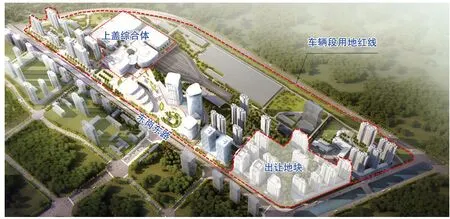
圖2 東崗車輛段綜合開發(fā)整體鳥瞰圖
(2)多方協(xié)同聯(lián)動,形成一體化設(shè)計(jì)機(jī)制。即車輛段及車輛段上蓋綜合體兩方的建設(shè)責(zé)任主體和各設(shè)計(jì)單位在車輛段上蓋開發(fā)的推進(jìn)過程中應(yīng)一體聯(lián)動,建立“統(tǒng)籌協(xié)調(diào)調(diào)度、多業(yè)主協(xié)同、多設(shè)計(jì)單位聯(lián)合”的協(xié)同規(guī)劃設(shè)計(jì)機(jī)制,形成“規(guī)劃設(shè)計(jì)一張圖、建設(shè)實(shí)施一張表”,通過規(guī)劃統(tǒng)籌、業(yè)主協(xié)同、設(shè)計(jì)互認(rèn)的工作機(jī)制,確保項(xiàng)目建設(shè)有序高效地推進(jìn)。
4 一體化設(shè)計(jì)關(guān)鍵技術(shù)
4.1 空間布局一體化
東崗車輛段上蓋開發(fā)與相鄰地塊開發(fā)無縫銜接、一體化設(shè)計(jì),實(shí)現(xiàn)上蓋綜合體與相鄰地塊地下、地上空間的便捷連通、整體利用,形成立體化、復(fù)合化、一體化的開發(fā)空間,為全面提升上蓋綜合體價值提供基礎(chǔ)空間保障。
4.1.1 上蓋綜合體與相鄰地塊地下空間的連通
東崗車輛段上蓋綜合體的主體位于車輛段運(yùn)用庫頂板之上。為使其與相鄰地塊的地下空間連通,在設(shè)計(jì)時采用了擴(kuò)大上蓋綜合體的局部區(qū)域并使其落地的方式,即在上蓋綜合體的落地區(qū)域下部設(shè)置2 層地下室與相鄰地塊的地下室連通,并同時在該區(qū)域設(shè)置6 部垂直電梯,進(jìn)一步加強(qiáng)上蓋綜合體與相鄰地塊地下空間的聯(lián)系(圖 3)。
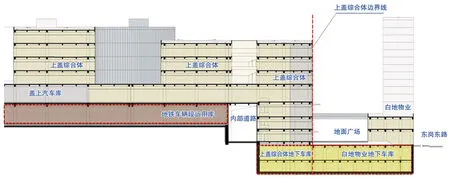
圖3 上蓋綜合體與相鄰地塊地下空間連通示意圖
4.1.2 上蓋綜合體與相鄰地塊地上空間的相互滲透
東崗車輛段上蓋綜合體與城市道路高差約16 m。設(shè)計(jì)人員充分利用場地高差,通過設(shè)置層層錯落的景觀平臺,引入景觀小品、地面景觀綠帶等,形成具有強(qiáng)烈空間引導(dǎo)性的慢行商業(yè)休閑空間,在使上蓋綜合體與相鄰地塊的地上部分融為一體、構(gòu)成一體化連續(xù)室外空間的同時,指引客流向上蓋綜合體集聚(圖4)。

圖4 上蓋綜合體東北側(cè)入口景觀平臺效果圖
4.2 交通規(guī)劃一體化
交通規(guī)劃作為本項(xiàng)目設(shè)計(jì)的重要組成部分,深度融合到從前期立項(xiàng)開始的整個設(shè)計(jì)過程中,從區(qū)域交通一體化、上蓋綜合體內(nèi)外交通疏解等方面對項(xiàng)目周邊交通設(shè)施進(jìn)行全面優(yōu)化和提升,打造暢通融合的上蓋綜合體交通系統(tǒng)。
4.2.1 上蓋綜合體與其周邊區(qū)域交通規(guī)劃設(shè)計(jì)一體化
在項(xiàng)目立項(xiàng)階段,交通規(guī)劃先期介入,從區(qū)域交通層面對上蓋綜合體及其周邊區(qū)域路網(wǎng)的通行能力進(jìn)行一體化考慮。通過對本項(xiàng)目建設(shè)前后周邊路網(wǎng)高峰小時交通飽和度進(jìn)行模擬分析可知,車輛段上蓋綜合體建成后,所產(chǎn)生的誘增交通量對周邊道路及交叉口存在一定影響,尤其是對項(xiàng)目北側(cè)東崗東路的影響較大,將導(dǎo)致項(xiàng)目周邊道路交通飽和度普遍上升,交叉口通行能力下降(圖5)。此外,由于項(xiàng)目區(qū)域內(nèi)路網(wǎng)已經(jīng)接近飽和,無法承受更大的交通量,因此需對周邊路網(wǎng)配套設(shè)施進(jìn)行優(yōu)化。

圖5 項(xiàng)目建設(shè)前后周邊路網(wǎng)高峰小時飽和度模擬對比(單位:pcu/h)
項(xiàng)目北側(cè)東崗東路原地面道路為雙向6 車道,非機(jī)動車道僅1.5 m 寬,在公交車停靠及路邊違章停車的情況下,實(shí)際使用車道數(shù)僅為4 車道。考慮非機(jī)動車道寬度及港灣式公交站點(diǎn)的布置,在項(xiàng)目立項(xiàng)階段提出結(jié)合地鐵站點(diǎn)施工,將東崗東路道路紅線拓寬至雙向8 車道標(biāo)準(zhǔn),并將配套的港灣式公交站點(diǎn)一次性實(shí)施到位的建議。該建議在項(xiàng)目實(shí)施過程中得到落實(shí)。
4.2.2 實(shí)施全過程交通設(shè)計(jì),提升交通與建筑的匹配度
在項(xiàng)目整個設(shè)計(jì)過程中,設(shè)計(jì)人員從上蓋綜合體車行出入口的選擇以及各層面車行交通流線組織等方面全面優(yōu)化交通設(shè)計(jì)(圖6),使項(xiàng)目內(nèi)道路能夠更有效與城市道路快速連接,進(jìn)而構(gòu)建高效、便捷、可持續(xù)發(fā)展的上蓋綜合體交通系統(tǒng)。在項(xiàng)目車庫建設(shè)階段,設(shè)計(jì)人員根據(jù)建設(shè)單位需求和當(dāng)前“智慧交通”的發(fā)展趨勢,進(jìn)行車庫的專項(xiàng)交通組織設(shè)計(jì)和交通標(biāo)識設(shè)計(jì),進(jìn)而提升項(xiàng)目的交通便利性和可識別性。
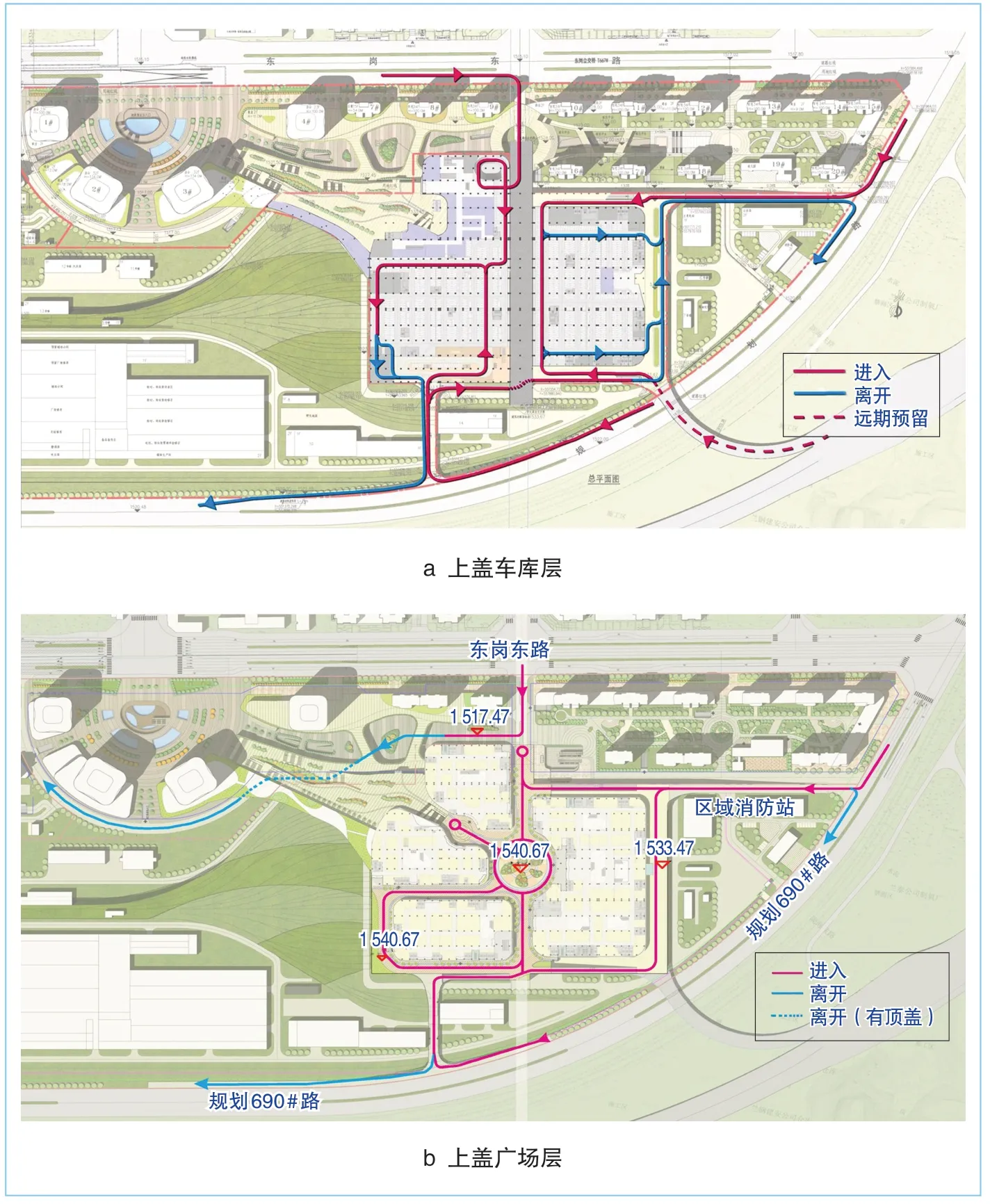
圖6 上蓋綜合體各層面車行交通流線(單位:m)
4.3 結(jié)構(gòu)設(shè)計(jì)一體化
東崗車輛段運(yùn)用庫屬于工業(yè)生產(chǎn)用房,其頂板之上為上蓋綜合體,二者一體化規(guī)劃設(shè)計(jì),同步建設(shè),分期投用。設(shè)計(jì)人員對二者的結(jié)構(gòu)進(jìn)行一體化設(shè)計(jì),選擇合理的結(jié)構(gòu)體系和柱網(wǎng),加強(qiáng)結(jié)構(gòu)計(jì)算分析,充分考慮上蓋開發(fā)荷載預(yù)留等技術(shù)措施,從而實(shí)現(xiàn)安全、合理的結(jié)構(gòu)設(shè)計(jì)。
4.3.1 一體化結(jié)構(gòu)體系分析和柱網(wǎng)布置
項(xiàng)目規(guī)劃建設(shè)單位經(jīng)過多輪功能業(yè)態(tài)策劃分析,確定本項(xiàng)目的功能業(yè)態(tài)為上蓋綜合商業(yè)體兼顧辦公物業(yè)。設(shè)計(jì)人員根據(jù)上蓋綜合體的功能業(yè)態(tài)類型及蓋下運(yùn)用庫的工藝及限界要求,綜合考慮造價成本,通過對多種方案進(jìn)行比選,確定本項(xiàng)目結(jié)構(gòu)采用框架結(jié)構(gòu)體系,而且不進(jìn)行結(jié)構(gòu)轉(zhuǎn)換。為滿足工藝和限界要求,運(yùn)用庫采用大跨度柱網(wǎng)布置,上蓋綜合體采取與蓋下運(yùn)用庫共用柱網(wǎng)的結(jié)構(gòu)形式,以提高結(jié)構(gòu)整體抗震性能。此外,還通過采取將上蓋綜合體建筑層高加大至5.5 m、部分設(shè)備管線穿梁等措施,保障上蓋綜合體的室內(nèi)凈高要求 (圖 7)。
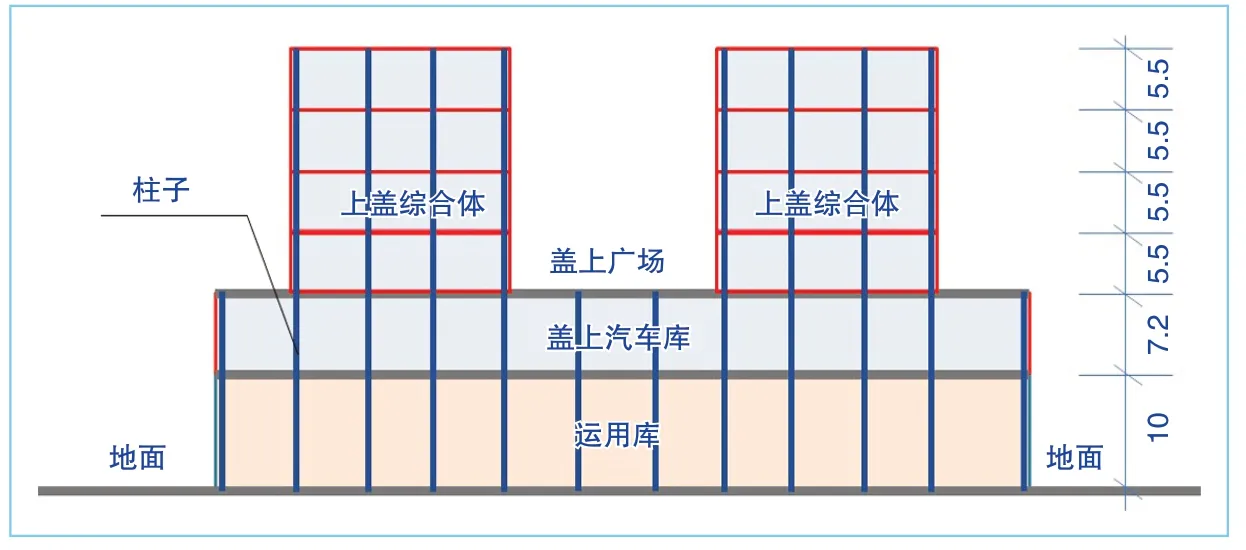
圖7 一體化結(jié)構(gòu)布置示意圖(單位:m)
4.3.2 一體化結(jié)構(gòu)設(shè)計(jì)預(yù)留措施
東崗車輛段及其上蓋綜合體采用一體化設(shè)計(jì)、同步建設(shè)、分期投用的建設(shè)策略,在對二者進(jìn)行一體化結(jié)構(gòu)設(shè)計(jì)時,設(shè)計(jì)人員采取了如下預(yù)留措施:根據(jù)上蓋綜合體不同功能業(yè)態(tài)所對應(yīng)的不同荷載需求,對車輛段結(jié)構(gòu)及其基礎(chǔ)進(jìn)行經(jīng)濟(jì)合理的包容性設(shè)計(jì);對于作為上蓋開發(fā)施工作業(yè)基本面的車輛段頂板,充分考慮施工荷載,為其預(yù)留后續(xù)上蓋開發(fā)施工作業(yè)的荷載條件。
4.4 消防設(shè)計(jì)一體化
由于車輛段上蓋綜合體與車輛段的功能類型不同,其消防設(shè)計(jì)必然存在諸多差異,但鑒于二者上下疊加、組合建造的實(shí)際情況,應(yīng)對其消防設(shè)計(jì)進(jìn)行統(tǒng)一考慮、一體化設(shè)計(jì)。
4.4.1 完善內(nèi)外部消防救援設(shè)施及措施
由于東崗車輛段上蓋綜合體與東崗東路城市道路高差較大(約16 m),加之其在蓋上16 m 及23.20 m 標(biāo)高處分別設(shè)置集散廣場及具備消防撲救條件的室外場地,建筑空間關(guān)系復(fù)雜,因此為確保消防救援安全,本項(xiàng)目采取以下消防保障措施:從2個不同方向設(shè)置直接連通城市道路的外部消防救援通道,使外部消防救援力量能夠進(jìn)入(圖8);在項(xiàng)目建設(shè)過程中,加強(qiáng)與消防驗(yàn)收及救援部門的溝通,使相關(guān)單位提前了解項(xiàng)目的消防設(shè)施狀況;在項(xiàng)目投入使用之前,通過與消防救援部門進(jìn)行聯(lián)合演練,完善項(xiàng)目本身的消防措施,加強(qiáng)早期火情下的自救能力。
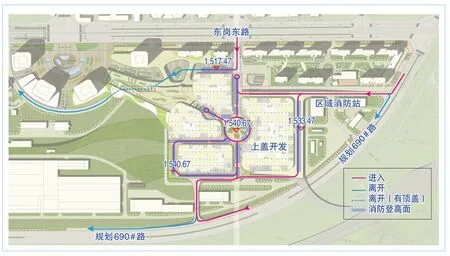
圖8 消防登高面及消防車流線示意圖(單位:m)
4.4.2 上蓋綜合體與蓋下運(yùn)用庫一體化消防設(shè)計(jì)
對于車輛段上蓋綜合體,設(shè)計(jì)人員根據(jù)GB 50016-2014《建筑設(shè)計(jì)防火規(guī)范》中關(guān)于商業(yè)或辦公建筑的設(shè)計(jì)要求,綜合考慮其建筑規(guī)模,將其防火等級確定為一級。對于屬于工業(yè)廠房類建筑的車輛段運(yùn)用庫,GB 50016-2014《建筑設(shè)計(jì)防火規(guī)范》中規(guī)定其防火等級應(yīng)不低于二級,但通過與消防審查部門進(jìn)行溝通,考慮到其位于上蓋綜合體下部,故確定其防火等級不低于上蓋綜合體,即也為一級。
4.5 公共空間景觀一體化
上蓋綜合體既是城市的一部分,應(yīng)合理地融入城市,成為其有機(jī)組成部分,又要凸顯自身特色,提升物業(yè)的可識別性。
4.5.1 上蓋建筑與城市區(qū)域景觀一體化
為有效解決地鐵線路及其附屬建筑割裂城市景觀的問題,本項(xiàng)目設(shè)計(jì)人員利用上蓋開發(fā)和相鄰地塊開發(fā)的契機(jī),沿著東崗東路設(shè)計(jì)了一條連續(xù)、完整的城市景觀帶(圖 9),形成開放的室外活動空間,使新建建筑與城市景觀融為一體、彼此滲透、相互補(bǔ)充,共同打造區(qū)域一體化的景觀空間。
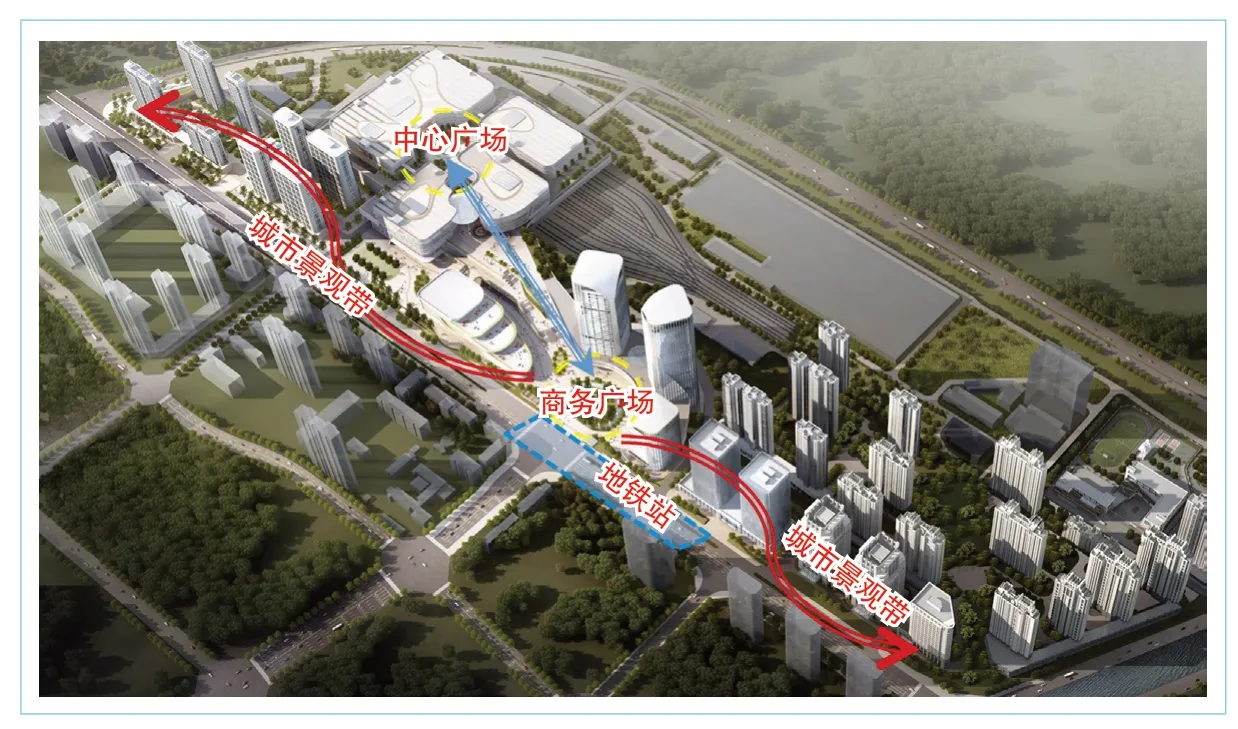
圖9 上蓋建筑與城市景觀的一體化
4.5.2 上蓋建筑與其室外公共空間景觀一體化
不同的上蓋開發(fā)功能業(yè)態(tài)需搭配與之相呼應(yīng)的室外公共空間景觀,從而形成開放的、獨(dú)具特色和活力的物業(yè)綜合體。本項(xiàng)目設(shè)計(jì)人員以蘭州市花——玫瑰花為靈感,以“金絲玉帶,錦簇花團(tuán)”為設(shè)計(jì)理念,綜合考慮消防救援、人員戶外活動等功能需求,對上蓋綜合體建筑體塊進(jìn)行化整為零的體形組合設(shè)計(jì),使其自然形成花朵狀外觀,同時結(jié)合第五立面的景觀設(shè)計(jì),強(qiáng)化設(shè)計(jì)理念,實(shí)現(xiàn)上蓋建筑與其室外公共空間景觀的相互呼應(yīng)、相得益彰。
5 結(jié)語
本文結(jié)合蘭州市軌道交通1 號線東崗車輛段上蓋綜合開發(fā)項(xiàng)目一體化設(shè)計(jì)與建設(shè)的工程實(shí)踐,對地鐵車輛段上蓋綜合開發(fā)一體化設(shè)計(jì)理念、一體化設(shè)計(jì)關(guān)鍵技術(shù)等進(jìn)行闡述和分析,以期為類似項(xiàng)目提供參考和借鑒。

