無電壓傳感器的光伏MPPT研究
王長云+李春蘭+曹成帥+汪澤


摘 要: 最大功率點跟蹤在光伏陣列工作時發揮著重要作用,針對目前采用的最大功率點跟蹤算法均需要計算功率,提出了一種無電壓傳感器的改進型控制策略。該方法基于DC?DC變換器輸入電流的控制,通過變步長調節實現占空比自尋優,使光伏陣列輸出最大功率,算法實現過程不需要功率計算。最后通過仿真對該方法進行驗證和測試,結果表明,該方法能準確實現最大功率跟蹤,同時動態響應特性和穩定性也較好。
關鍵詞: 光伏陣列; 最大功率點跟蹤; 控制策略; 自尋優
中圖分類號: TN820.4?34 文獻標識碼: A 文章編號: 1004?373X(2017)18?0135?04
Study on photovoltaic MPPT without voltage sensor
WANG Changyun, LI Chunlan, CAO Chengshuai, WANG Ze
(College of Mechanical Engineering and Traffic, Xinjiang Agricultural University, Urumqi 830052, China)
Abstract: Maximum power point tracking (MPPT) plays an important role in PV array working. The power need be calculated in available MPPT algorithms, therefore an improved control strategy without any voltage sensor is presented. The method, on the basis of the control of input current of DC?DC converter, realizes the self?optimization of duty cycle by means of step size varying, and makes the PV array output maximum power, by which the power needn′t be calculated in algorithm realization process. The method was tested and verified with simulation. The simulation results show that the method can realize the maximum power tracking accurately, and has perfect dynamic response characteristic and stability.
Keywords: PV array; MPPT; control strategy; self?optimization
0 引 言
隨著分布式電源發電技術的發展,光伏發電得到大規模的應用。相應的,光伏陣列控制技術成為了研究熱點,而最大功率點跟蹤(MPPT)技術因其可以提高光伏陣列的工作效率,得到了廣泛關注。目前常用的MPPT技術主要有恒定電壓法[1]、擾動觀察法[2]和電導增量法[3]。恒定電壓法控制策略簡單易于實現,但其在外界條件變化后功率曲線會發生偏移,而無法工作在最大功率點(MPP)。擾動觀察法概念清晰,簡單可靠,但控制精度與響應速度存在矛盾。電導增量法需要高速的A/D采樣,對硬件要求較高,實現較為困難,外界條件突變時,還可能誤判。為此有研究提出包括模糊控制[4?5]、自尋優控制[6]等的改進方法。采用模糊控制對上述方法改進可以一定程度上優化策略,但跟蹤效果與模糊表的選擇有關,模糊表制定的優劣很大程度上取決于設計者的經驗。以上MPPT技術雖各有優點,但大都需要采樣光伏陣列的輸出電壓、電流并計算功率。為了簡化電路結構,優化控制策略,本文提出一種不需要功率計算的無電壓檢測自尋優MPPT策略,并通過Matlab仿真驗證其有效性。
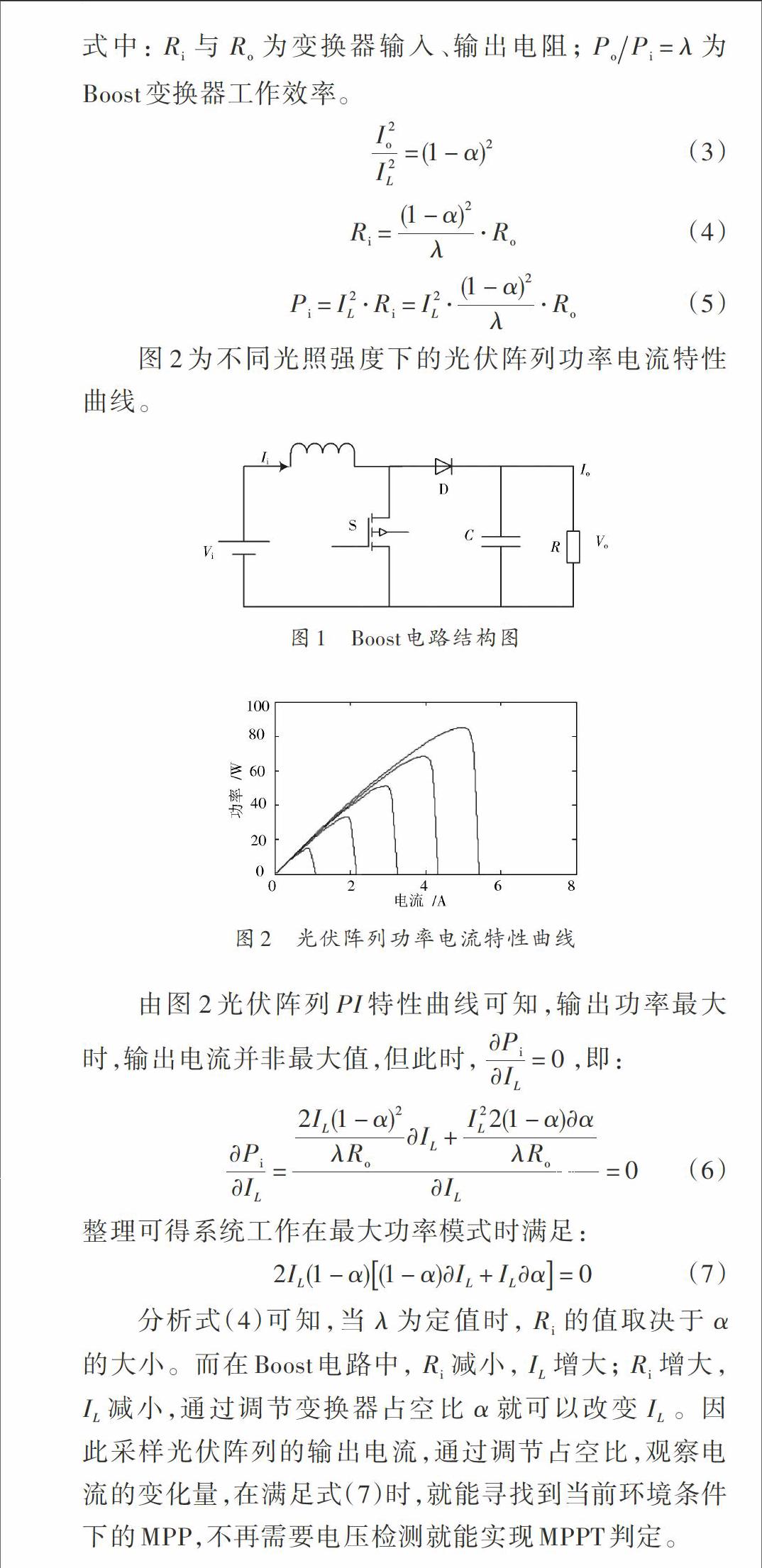
2 無電壓檢測的MPPT策略實現
當光伏電池工作條件確定后,式(6)中[1λRo]隨之確定并可視為常數,因此[2IL(1-α)2+2IL21-α?α?IL]的正負決定了[?Pi?IL]的正負。當其結果為正時,當前電感電流小于最大功率電流,系統工作在最大功率點左側,需要減小變換器占空比至式(7)成立;反之則需要增大變換器占空比。但是,這種方法的固有缺點也使得其應用受到一定的限制:擾動步長[?α]的選擇使得跟蹤速度與精度間存在矛盾,[?α]較小可以提高MPPT精度,但跟蹤時間會延長。對于光伏電池這類很依賴于外界環境的發電設備,時間越久,未知性越大;相反的[?α]較大可提高速度,卻相對的犧牲了精度,使得跟蹤的波動性變大。
根據變步長的思想[8?9],結合第1節的原理,提出適用于無電壓檢測的變步長MPPT控制策略。當[2IL(1-α)2+2IL21-α?α?IL]值較大時說明距離最大功率點較遠,可以采用較大步長縮短尋優時間,隨著工作狀態的調整,[2IL(1-α)2+2IL21-α?α?IL]不斷降低,至一定區間后,可以改為小步長,改善尋優精度。傳統變步長將第二段擾動設為定值,使得步長選擇對控制效果影響顯著,這無疑降低了控制策略的通用性。為了彌補這一缺點,本文將第二段步長改為變量,隨著系統工作點逐漸接近MPP,每次的擾動步長取上一時刻擾動步長的[12]。這樣不僅降低了對擾動步長選擇的要求,提高了策略通用性,還實現了光伏陣列工作點越遠離MPP,追蹤速度越大,越接近MPP,系統振蕩越小的目的。
隨著擾動步長的每次減半,若不加以限制可能出現控制策略實現時實際擾動輸出值[Δk]接近于零,此時擾動近乎于無,系統無法達到最大功率輸出。因此需要設置極小值[ε]避免這一情況。本文取[ε=5×10-4]。endprint
變步長判斷條件的設置將會影響控制效果。如果取值過小,系統極易進入最大功率點右側,此時最大功率判斷條件為負,功率變化對擾動更加敏感,為控制帶來不利;如果取值過大,則較早進入短步長擾動,追蹤時間加長,無法發揮變步長的優越性。由圖2可知,無論當前的功率點位于最大功率點左側還是右側,隨著輸出功率越來越接近最大功率點,PI曲線的斜率絕對值[?Pi?IL]呈逐漸減小趨勢。因此,可在基本擾動觀測法的基礎上,添加對爬坡斜率的再判斷,作為變步長交界點的判斷依據。經過驗證,本文變步長的判斷條件設置為[?Pi?IL 本文采用改進兩級變速方式實現MPPT控制,其基本控制思路為: (1) 計算[?Pi?IL],若[?Pi?IL>tan15°],系統采用第一級擾動步長[Δk]=Spl; (2) 若[?Pi?IL≤tan15°],則使每次擾動步長為上次擾動值的[12],即[Δk+1=12Δk]; (3) 判斷[Δk>ε],若成立則輸出擾動值為[Δk],否則輸出擾動值為[ε]。 (4) 計算[2IL(1-α)2?IL+2IL21-α?α],若結果為正,則擾動方向不變,若結果為負,則將擾動反向。 (5) 檢測系統是否工作在MPP,是,則結束擾動,否,則重復上述步驟。 無電壓檢測的改進型MPPT控制流程如圖3所示。 3 仿真及分析 在Matlab/Simulink仿真環境下建立圖4所示的結構光伏系統仿真模型。 相關仿真參數設定:直流側電容均為500 μF,電感為5 mH,DC?DC電路為Boost型;光伏陣列短路為電流9.21 A,開路電壓為21 V,最大功率電流為8.57 A,最大功率電壓為17.4 V。光伏陣列工作溫度設為45 ℃,輸入光照強度為400 W/m2;初始占空比[α0]設為0.5。 為了說明本文提出的無電壓檢測的改進變步長MPPT策略控制效果的優良性,針對圖4仿真電路,分別采用傳統擾動觀察法、無電壓檢測的擾動觀測法及無電壓檢測的改進型擾動觀測法,通過相應的振蕩值、追蹤時間比較分析。仿真結果分別如圖5~圖7所示。初始擾動步長均設置為0.02。 由圖5~圖7可知,在仿真條件相同時,傳統的擾動觀測法輸出功率均值為83.7 W,振蕩值為8 W,追蹤時間為0.22 s;無電壓檢測MPPT輸出功率均值為84.1 W,振蕩值為3 W,追蹤時間為0.28 s;無電壓檢測的改進變步長輸出功率均值為84.3 W,振蕩值為1.2 W,追蹤時間為0.17 s。可以看出采用本文提出的無電壓檢測的改進變步長擾動觀測法可以有效減小輸出振蕩,加快追蹤速度。 4 結 論 本文在分析Boost型DC?DC變換器工作原理的基礎上,提出了一種基于變換器輸入電流控制,應用最大功率算法調節占空比,完成跟蹤的無電壓檢測的改進型MPPT。該方法無需功率計算,當光伏陣列工作環境變化時,先采用長擾動步長加速逼近MPP,至一定范圍后,每次的擾動步長改為前次擾動的[12],以此實現越接近MPP振蕩越小。通過Matlab/Simulink仿真驗證了這一方法的正確性。本算法具有結構簡單、成本低、追蹤速度快、效率高的優點。 參考文獻 [1] 汪義旺,曹豐文,張波,等.光伏發電系統最大功率點快速跟蹤控制研究[J].電力電子技術,2010(10):14?16. [2] ZHANG Chao, ZHAO Dean, WANG Jinjing, et al. A novel two?mode MPPT method for photovoltaic power generation system [C]// Proceedings of 2009 IEEE International Power Electronics and Motion Control Conference. [S.l.]: IEEE, 2009: 2100?2102. [3] 董密,楊建,彭可,等.光伏系統的零均值電導增量最大功率點跟蹤控制[J].中國電機工程學報,2010(21):48?53. [4] 徐鋒.一種基于模糊控制的光伏發電系統的MPPT控制[J].電源技術,2014(1):92?96. [5] AREDES M A, FRANCA B W, AREDES M. Fuzzy adaptive P&O control for MPPT of a photovoltaic module [J]. Journal of power and energy engineering, 2014, 2(4): 120?129. [6] 徐彭濤,趙巧娥,張強,等.基于中值觀測的自適應變步長MPPT算法研究[J].現代電子技術,2014,37(22):150?152. [7] 賀益康,潘再平.電力電子技術[M].北京:科學出版社,2011:152?156. [8] 胡義華,陳昊,徐瑞東,等.一種兩階段變步長最大功率點控制策略[J].電工技術學報,2010(8):161?166. [9] SUN Wen, ZOU Lixin, SUN Yaxiang. An improved MPPT method with variable step size for PV system [C]// Proceedings of 2011 4th IEEE International Conference on Computer Science and Information Technology. [S.l.]: IEEE, 2011: 1?4. [10] 張俊紅,魏學業,胡良.基于電路分析的串并聯光伏陣列特性研究[J].計算機仿真,2016,33(2):147?152.

