社會網絡頂點間相似性度量及其應用*

陳 曉，郭景峰，張春英

1.燕山大學 信息科學與工程學院，河北 秦皇島 066004

2.華北理工大學 遷安學院，河北 遷安 064400

3.河北省計算機虛擬技術與系統集成重點實驗室，河北 秦皇島 066004

4.華北理工大學 理學院，河北 唐山 063009

社會網絡頂點間相似性度量及其應用*

陳 曉1,2,3，郭景峰1,3+，張春英4

1.燕山大學 信息科學與工程學院，河北 秦皇島 066004

2.華北理工大學 遷安學院，河北 遷安 064400

3.河北省計算機虛擬技術與系統集成重點實驗室，河北 秦皇島 066004

4.華北理工大學 理學院，河北 唐山 063009

Abstract:Set pair analysis as the mathematical theory of dealing with the interaction system of certainty and uncertainty,can be used to deal with the complexity social network of uncertain relationship.Firstly,based on the application of set pair analysis theory,this paper takes social network as an identical-different-contrary system(certain and uncertain system).Based on set pair connection degree to descript the identical,different and contrary relations between vertices,considering the contribution of local features and the topological structure to the vertex similarity,this paper defines the similarity between vertices based on the relation connection degree taking into account weightand clustering coefficient.The measurement can better describe network structure characteristics,overcome the underestimating for some similarity between vertices based on traditional local structures,and reduce the computational complexity of global similarity indices.Secondly,in order to utilize the similarity indices to community discovering,combined with agglomerative hierarchical clustering algorithm,it is applicable to detect community structures in complex networks with any object that has similarity measurement.Finally,through the experiment of community mining on the social network,and compared with the typical algorithms of community discovering,the experimental results verify the correctness and effectiveness of the similarity measurement.

Key words:social network;similarity;set pair;identical-different-contrary relations;community discovering

集對分析作為處理系統確定性與不確定性相互作用的數學理論，可用來處理存在不確定關系的復雜社會網絡。首先，應用集對分析理論，將社會網絡作為一個同異反系統（確定不確定系統），采用集對聯系度刻畫頂點間的同異反關系，綜合考慮頂點的局部特征和拓撲結構對頂點相似性的貢獻，提出加權聚集系數聯系度的頂點間相似性度量方法。該度量方法可以更好地刻畫網絡結構特征，克服傳統局部相似性度量指標對某些頂點間相似性值的低估，降低全局相似性度量指標的計算復雜度。其次，為了將該相似性度量指標應用于社區發現，與凝聚型層次聚類算法相結合，使其適用于具有相似性度量對象的復雜網絡社區發現問題。最后，在社會網絡上進行社區挖掘實驗，并與經典社區發現算法進行比較，實驗結果表明了該相似性度量指標的正確性及有效性。

社會網絡；相似性；集對；同異反關系；社區發現

1 引言

隨著社會網絡分析在各領域的廣泛應用，社會網絡分析技術[1]受到國內外學者的廣泛關注，已成為當前的研究熱點。社會網絡分析技術以圖論為基礎，通常將社會網絡表示為一個二元組G=(V,E)，其中頂點集V代表網絡中的個體，邊集E代表網絡中個體間的聯系。頂點間相似性的度量方法作為社會網絡分析的基礎，對社區發現、社區演化和鏈接預測具有重要的理論意義實用價值。

現有頂點間相似性[2]的計算方法主要分為3類：（1）基于網絡全局信息的相似性度量指標，如Katz指標[3]、LHN（Leicht-Holme-Newman）指標[4]、ACT（average commute time）指標[5-6]、RWR（random walk with restart）指標[7]等；（2）基于頂點公共鄰居的局部相似性度量指標，如 CN（common neighbor）指標[8]、Salton（又稱為Cosine）指標[9]、Sφrensen指標[9]、Jaccard指標[10]等；（3）介于全局和局部之間的半局部相似性度量指標，如LP（local path）指標[11]、LRW（local random walk）指標[12]、RALP（resource allocation along local path）[13]等。其中，全局相似性度量指標需要考慮網絡的整體結構關系，通常利用網絡的鄰接矩陣計算逆矩陣和矩陣的特征根，或通過遍歷頂點間路徑度量相似性等。全局性方法雖然擁有相對較高的精度，但卻具有較高的時間和空間復雜度，不適宜較大規模的網絡。文獻[14]的研究表明，當路徑長度從2增加到5時，可以增大相似性的精度，而當路徑長度大于5時，相似性精度變化很小。局部相似性度量指標由于僅考慮頂點的最近鄰，具有較低的時間復雜度，卻低估了直接連接頂點間和通過關聯路徑連接的頂點間的相似性。因此，僅利用網絡個體間相同的確定性評估頂點間的相似性，不能全面體現網絡中個體間的關系。如何基于網絡中的確定與不確定關系，更準確地定義頂點間的相似性是本文的研究重點。

集對分析[15]（set pair analysis，SPA）理論是我國學者趙克勤于l989年提出的理論方法，是一種用聯系度統一處理模糊、隨機和信息不完全所致不確定性系統的理論和方法，在科學技術和社會經濟的許多領域得到了廣泛應用。2011年，文獻[16]首先將集對理論應用到社會網絡分析中，提出了集對社交網絡分析模型及其性質，為基于集對理論的社會網絡分析研究拉開了序幕。2013年，文獻[17-18]基于集對理論和共同鄰居提出了一種新的頂點間相似性度量方法，并根據社會網絡特性分別實現了靜態和動態α關系社區的挖掘算法，證明了α關系社區的挖掘更能體現社區存在的動態性。2014年，文獻[19]基于屬性圖提出了集對社交網絡實體相似性的計算方法，并基于集對態勢實現了社區發現。然而，現有基于集對的頂點間相似性度量方法，僅考慮了網絡中不確定的共同鄰居屬性數量對社區形成及網絡分析的影響，忽略了頂點間的拓撲結構、頂點的度等對頂點間相似性的影響。

本文將無向無權無符號的社會網絡作為研究對象，基于集對分析理論的思想，將社會網絡作為一個同異反系統（確定不確定系統），在考慮頂點度和頂點間拓撲結構兩個因素對頂點相似度的影響前提下，提出了一種新的頂點間相似性度量指標——加權聚集系數聯系度。為了更深入地驗證本文提出的頂點間相似性度量方法，將該相似性指標應用到社會網絡社區發現中，通過實驗結果進一步驗證頂點間相似性度量指標的正確性及有效性。

本文主要貢獻如下：

（1）提出加權聚集系數聯系度的頂點間相似性度量方法。綜合考慮網絡局部關系（共同鄰居等）和網絡拓撲結構屬性（聚集系數和頂點間路徑等），采用聯系度刻畫影響頂點間相似性的頂點集合的同異反關系，提出加權聚集系數聯系度的頂點間相似性度量方法。該方法根據宏觀異（不確定）關系F和微觀異（不確定）關系i轉化為同關系S時對頂點間相似性的貢獻，考慮頂點間連接密度影響，采用頂點的聚集系數作為i的取值方法；根據頂點度和頂點間路徑對相似性貢獻的影響，為同異反關系進行加權。該方法既避免了從單一數量上考慮頂點間同異反關系的不全面性，又避免了計算頂點間路徑的復雜性，不僅更好地體現網絡拓撲結構特點，而且可以提高相似性指標的精確性。

（2）提出頂點間相似性優先凝聚和社區間均值凝聚相結合的層次聚類算法VSFCM（vertices similarity first and communities mean）。傳統基于平均距離的凝聚型層次聚類算法有大量更新平均距離的操作并且有社區聚類不合理現象。為了確保相似性大的頂點在同一社區中，相似性小的頂點在不同社區中，提出VSFCM算法，即將相似性大的頂點對優先合并為小社區，然后再進行社區間的合并，有效避免了頻繁更新操作，提高了算法效率。

本文組織結構如下：第2章介紹頂點間相似性度量指標的研究現狀；第3章討論基于聯系度的頂點間相似性模型及定理；第4章對社區發現算法進行描述；第5章通過實驗驗證頂點間相似性度量指標的正確性和合理性；最后總結全文，并對下一步工作進行展望。

2 相關工作及問題定義

現有多種計算頂點間相似性的方法，其中基于鄰接點（局部）的相似性方法具有較低的時間復雜度，文獻[2]研究結果表明，指標RA（resource allocation）的計算精度最佳，CN次之；基于路徑（全局）的相似性方法具有較高的時間復雜度，但具有較好的計算精度，如Katz；基于聯系度的方法是一種介于局部和全局之間的半全局方法，是借鑒同異反關系定義相似性的新方法。因此，主要介紹CN、RA、Katz和現有兩種基于聯系度的頂點間相似性定義方法。

2.1 基于鄰接點（局部）的相似性方法

公共鄰居CN指標[8]如式（1）所示：

資源配置RA指標[11]如式（2）所示：

2.2 基于路徑（全局）的相似性方法

Katz指標[3]如式（3）所示：

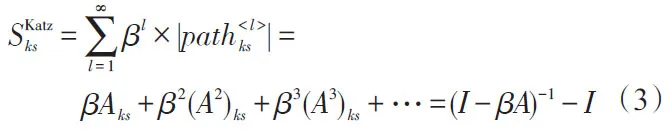
通過實驗證明β=0.000 5的實驗效果較好[20]，并保證指標收斂于(I-βA)-1-I。

2.3 基于聯系度的相似性方法

集對理論的基本定義和性質可以見文獻[15]。

文獻[17-18]首先將聯系度應用于社會網絡分析領域，以網絡結構為基礎，令頂點vk和vs為兩個研究對象，將頂點間的鄰接關系作為頂點屬性，兩個頂點的共有屬性記為N，則頂點間相似性度量指標定義如下。

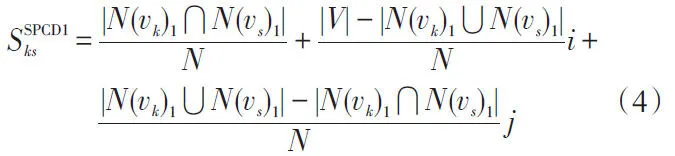
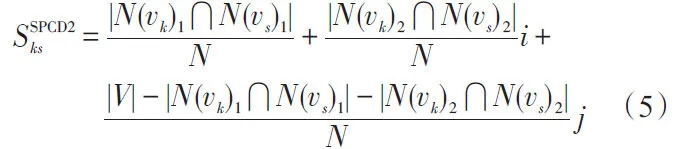
注：N(v)1表示頂點v的1級鄰居；N(v)2表示頂點v的2級鄰居，具體定義詳見下節。

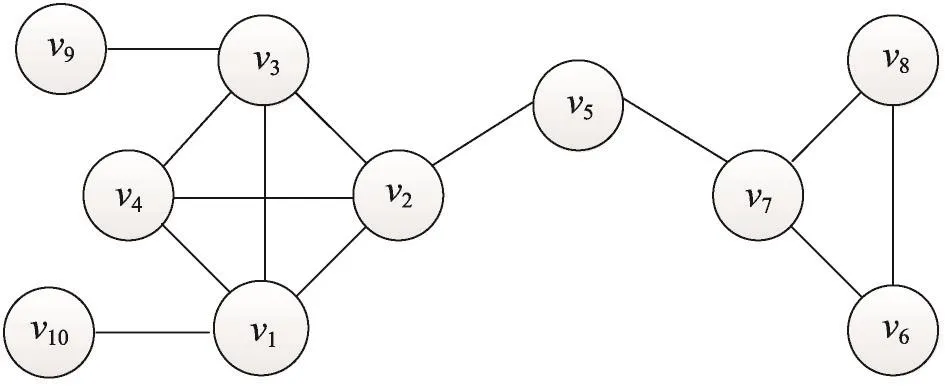
Fig.1 Instance networkA圖1 實例網絡A

3 基于聯系度的頂點間相似性模型

基于聯系度刻畫頂點間相似性度量工作的重點是，如何定義影響頂點間相似度的頂點集合的同異反關系。為了更好地表達鄰居頂點對頂點間相似性的影響，介紹相關定義如下。

3.1 相關定義

定義1（頂點鄰居集）給定社會網絡G=(V,E),?vk∈V，vk的1級鄰居集記為N(vk)1，如式（6）所示。

vk的2級鄰居集記為N(vk)2，如式（7）所示。

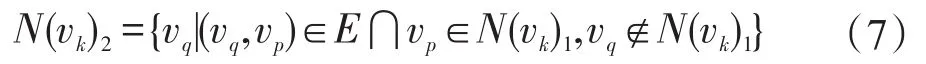
定義2（頂點的共同鄰居集）給定社會網絡G=(V,E)，?vk,vs,vq∈V，若vq∈N(vk)1?N(vs)1，則vq為vk和vs的共同1級鄰居。vk和vs的共同1級鄰居集記為CN(vk,vs)1，如式（8）所示。

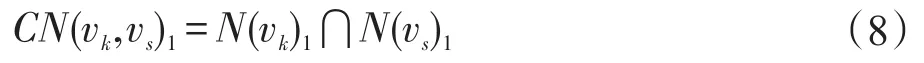
同理vk和vs的共同2級鄰居集記為CN(vk,vs)2,如式（9）所示。

同理vk和vs的共同1?2級鄰居集記為CN(vk,vs)1?2,如式（10）所示。

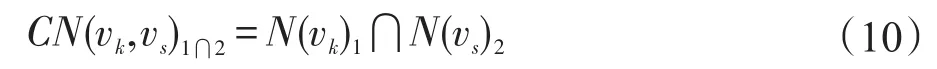
同理vk和vs的共同2?1級鄰居集記為CN(vk,vs)2?1,如式（11）所示。

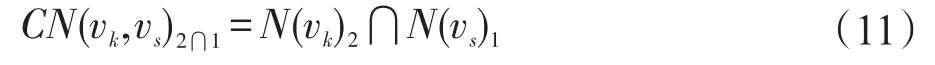
vk和vs的鄰居集關系如圖2所示。其中，代表CN(vk,vs)1，代表CN(vk,vs)1?2或CN(vk,vs)2?1，代表CN(vk,vs)2。

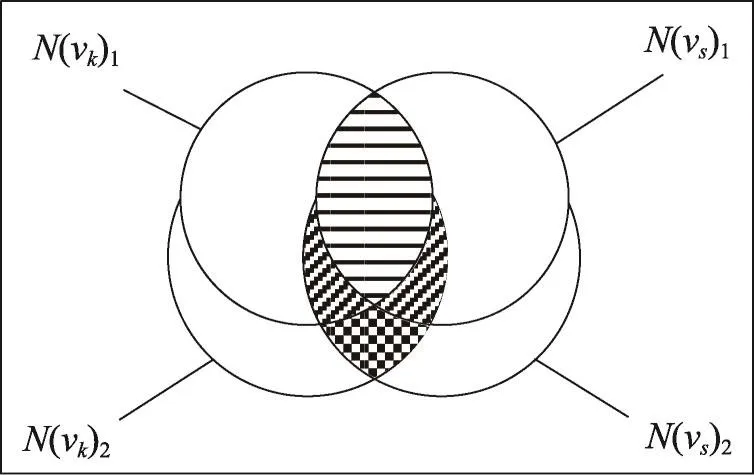
Fig.2 Neighbors set relation betweenvkandvs圖2 頂點vk和vs的鄰居集關系

3.2 頂點間相似性模型

在基于網絡拓撲結構的頂點間相似性度量方法中，如果兩個頂點間共同鄰居和短路徑越多，可能使得兩個頂點的相似性越強。基于這一思想，將兩個頂點的共同1級鄰居作為相同屬性，將1?2、2?1和2級鄰居作為宏觀層次上的不確定屬性，可以更好地刻畫不確定屬性對相同的確定屬性的影響。具體頂點間同異反關系定義如下。

定義3（頂點間同異反關系）給定社會網絡G=(V,E),?vk,vs∈V，相同屬性為vk和vs的共同1級鄰居，即S=|CN(vk,vs)1|；相異屬性為vk和vs的共同1?2、2?1和2級鄰居，即F=|CN(vk,vs)1?2|+|CN(vk,vs)2?1|+|CN(vk,vs)2|;其余為vk和vs的相反屬性，即P=N-S-F，其中，N=|V|。

然而，如果僅從頂點間同異反關系的個數方面刻畫頂點間的相似性，將存在明顯的局限性和不合理性。因此，為了更準確地刻畫頂點間的相似性，本文綜合考慮網絡密度和頂點度等特征，對各屬性關系進行加權，提出基于加權聚集系數的頂點間聯系度，具體定義如下。

定義4（相似性指標WCCD（weighted clustering coefficient connection degree））給定社會網絡G=(V,E),?vk,vs∈V，基于加權聚集系數的頂點間聯系度SWCCDks如式（12）所示。

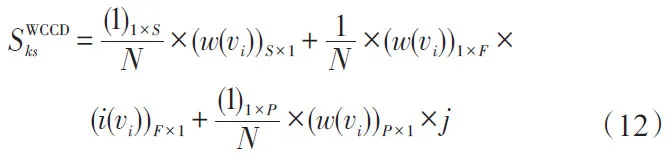
其中，N、S、F、P的含義如定義3所示，(1)1×S、(1)1×F和(1)1×P分別代表相同、相異和相反屬性的行向量，向量值均為1；w(vi)為頂點對應的權值；(i(vi))F×1向量值為相異屬性頂點vi對應的差異i值，j表示相反屬性的標記作用。

式（12）中存在3個參數(i(vi))F×1、w(vi)和j，這3個參數如何取值對計算頂點間聯系度起著至關重要的影響，下面主要介紹這3個參數的取值方法。

3.2.1i的取值方法

基于集對理論思想，i作為微觀層次上的差異標記，如何取值對不確定屬性如何向確定屬性轉換有著至關重要的影響。現有基于灰度[21]等的取值方法不能直接應用于社會網絡中頂點間相似性的計算中，需要重新定義差異標記i的取值方法。

在圖2所示的網絡中，v2∈CN(v1,v7)1?2，v5∈CN(v1,v7)2?1,由于頂點v2和v5的不同，使得它們轉化為CN(v1,v7)1的可能性也是不同的。考慮到不同的不確定屬性向確定屬性轉換的不同可能性，針對不同屬性將i的取值轉化為一個向量組；考慮到網絡的密度結構特性，采用頂點的聚集系數[22]值來量化該不確定屬性的i值。由于不確定屬性包括頂點對的共同1?2、2?1和2級鄰居，分別考慮上述3種情況轉換為共同1級鄰居的可能性來量化i值，具體計算方法如下。

3.2.2w的取值方法

在圖1所示的網絡中，v2,v4∈CN(v1,v3)1，由于v2和v4度的值不同，可見它們對v1和v3聯系度的貢獻也不盡相同。基于“頂點度越小對聯系度的貢獻越大，頂點度越大對聯系度的貢獻越小”的啟發式思想，以及路徑的可達性以及轉移概率來描述頂點對聯系度的貢獻。本文中頂點類型主要分為直接相連，共同1、1?2、2?1和2級鄰居頂點等，下面分別介紹以上5種類型的頂點權值w(vi)的定義方法，其中d(vi)表示頂點vi的度。

3.2.3j的取值方法

在社區發現算法中，由于期望將相似性大的頂點劃分到同一社區，則更希望考慮頂點間相同屬性，以及不確定性屬性轉向相同屬性的程度，對頂點間相似性的貢獻值。因此，令式（12）中j=0，忽略對立屬性的影響，認為不確定屬性全部轉向相同屬性。

4 社會網絡的社區發現算法

社區發現的主要目的是將社會網絡G=(V,E)劃分為K個互不相交的子社區，使得，且Gki?Gkj=?(i≠j)，保證同一社區內頂點間的關系緊密，不同社區關系稀疏。因此，基于相似性的社區發現問題就可以轉化為基于相似性的凝聚層次聚類問題。為了實現社區發現，首先給出社區間相似性的計算方法。

定義5（社區間相似性）設CK=(VK,EK)和CS=(VS,ES)為社會網絡中的兩個社區，則社區CK和CS間的相似性表示社區間頂點對相似性的均值，記為Sim(CK,CS)，如式（13）所示。

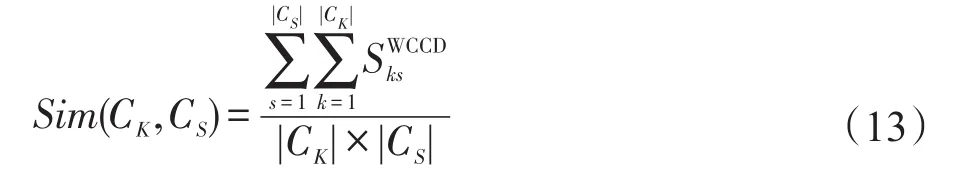
經典凝聚層次聚類AGNES（agglomerative nesting）算法[23]在進行社區合并時，首先計算頂點間的相似性值Sim(vk,vs)，其次選取max{Sim(vk,vs)}，然后將頂點vk和vs合并，記為Cnew。該方法在每次合并后，均需要重新計算Cnew與其他頂點或社區的相似性值，因此有大量Sim(Cnew,vi)值的更新操作。Sim(Cnew,vi)實質上是計算社區間頂點對的相似性均值，由于大社區中某頂點與獨立社區中頂點相似性較大，容易導致Sim(Cnew,vi)≥Sim(vj,vi)，即均值降低vi對大社區中相對距離較遠頂點（即相似性較低的頂點）的敏感性，導致vi不斷聚合到大社區中的現象，而不是優先合并相似性大的vi與vj。為了保證兩兩相似性大的頂點優先聚合，另一種方法實質上是比較每個頂點對的相似性度量是否均為最大值。即?vk∈V，當且僅當Sim(vj,vi)≥Sim(vj,vk), 且Sim(vj,vi)≥Sim(vi,vk)，將vi與vj合并，否則不合并。由于聚合條件嚴格，很難形成大規模社區。基于上述兩個方法的優缺點，考慮將兩種方法相結合。即將相似性值比較法融入到AGNES算法中，以減少社區間相似性值的計算次數，并避免頂點不斷聚合到大社區的現象；然后再將初步合并的社區按照AGNES算法進行聚合，以避免比較法中無法形成大規模社區的現象。因此，基于加權聚集系數聯系度，提出一種新的層次聚類算法VSFCM。具體算法描述如下。

算法1 VSFCM

輸入：社會網絡G=(V,E)的鄰接矩陣A

輸出：層次聚類樹

算法VSFCM主要分為三步：計算頂點間相似性，初始社區合并，非獨立社區合并。第一步：計算vk和vs間的相似性值SWCCDks。設社會網絡中頂點數N=|V|，基于聯系度思想的計算路徑長度為1至4步，路徑長度為5的頂點間相似性值為0。因此，僅需計算和存儲任意頂點vk與其4步內鄰居的相似性值。令任意頂點vk的4步內鄰居集個數為L，則空間復雜度為O(NL)。對于大部分實際網絡中，頂點的4級內鄰居集個數L的取值遠小于N，且L值不會隨著網絡規模的增長而快速增長，因此，適用于大規模網絡頂點間相似性的存儲。第二步：初始獨立社區合并，如代碼第3～13行。此步選取最大值的頂點對進行合并，因此，時間復雜度為O(NL)。第三步：非獨立社區合并，如代碼第14～18行。設有K個社區，K遠小于N，時間復雜度為O(K2)。社區發現算法VSFCM最終的時間復雜度為O(NL+K2)。

VSFCM算法是對經典層次聚類算法的改進，主要區別是，在聚類初期，僅通過判斷頂點間相似度先生成小規模的初始社區，并不進行新社區與原有社區間值的更新操作；在聚類期間，對初始社區進行合并，最終生成層次聚類樹。盡管合并順序不同，但VSFCM算法保證了其產生的結果和經典方法是相同的。

5 實驗結果與分析

實驗的硬件環境是Intel?CoreTMDuo E7500雙核的CPU，內存4 GB；軟件環境是Windows 7系統，Matlab R2012a。

主要從兩方面進行實驗驗證：（1）與現有頂點間相似性度量指標進行比較，驗證WCCD度量指標的合理性和正確性；（2）通過與經典社區發現方法進行比較，驗證WCCD度量指標在解決社區發現問題時的正確性和有效性。其中，利用模塊度函數評價社區結構的優劣。

模塊度函數（Q函數）是Newman[24]提出的衡量網絡劃分質量的標準。Q函數定義如下：

其中，K表示社區個數；m表示網絡連接總數；ms表示社區s中的連接總數；ds表示社區s中頂點度之和。Q函數的取值范圍是0～1之間。通常認為最大Q函數值對應的社區劃分為網絡社區的最佳劃分；Q函數值越接近于1，說明網絡的社區結構越明顯。在實際的網絡中，Q函數值通常在0.3～0.7之間。文獻[25]指出模塊度Q函數存在分辨率極限問題[26]，但當前未見其他更合適的評價指標，模塊度Q函數仍作為研究者們廣泛應用于評價社區質量的標準之一[27-28]。

5.1 相似性度量指標的實驗分析

為了驗證采用聯系度綜合刻畫網絡局部關系和網絡拓撲結構的頂點間相似性度量指標WCCD，比單一考慮局部關系、路徑及同異反數量的相似性度量指標具有更高的準確性，本文選取了經典的最具代表性的CN、RA和Katz相似性度量指標，選取了現有基于聯系度的SPCD1和SPCD2相似性度量指標，與本文提出的WCCD相似性度量指標進行比較。在模擬網絡[29]、空手道俱樂部Karate網絡[30]和Dolphin網絡[30]3種網絡中，如圖3所示，應用VSFCM算法進行社區挖掘，通過社區的劃分效果對6種頂點間相似性指標定義的合理性和正確性進行驗證。應用6種頂點間相似性度量指標，利用VSFCM算法進行層次聚類，選取模塊度最大的層作為社區劃分結果，各度量指標的網絡最大模塊度值、社區個數對比情況如表1所示。

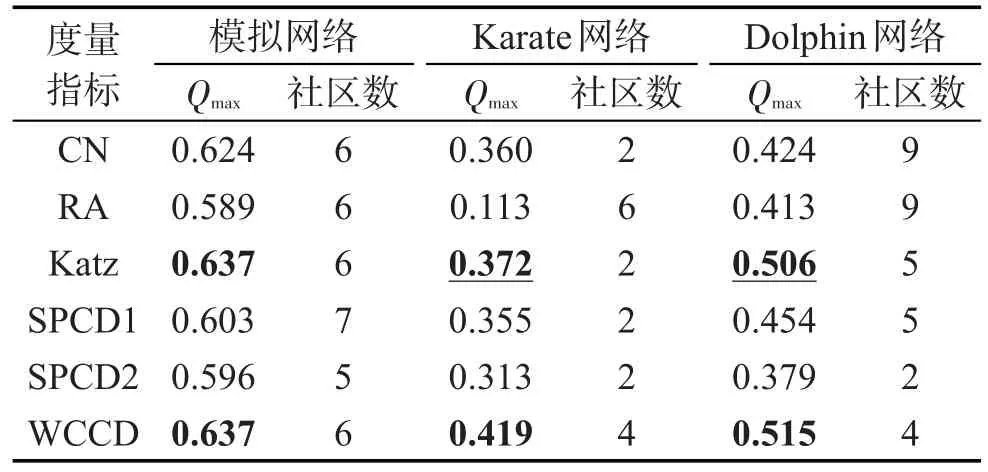
Table 1 Experimental results of 6 indicators表1 6種指標的實驗結果

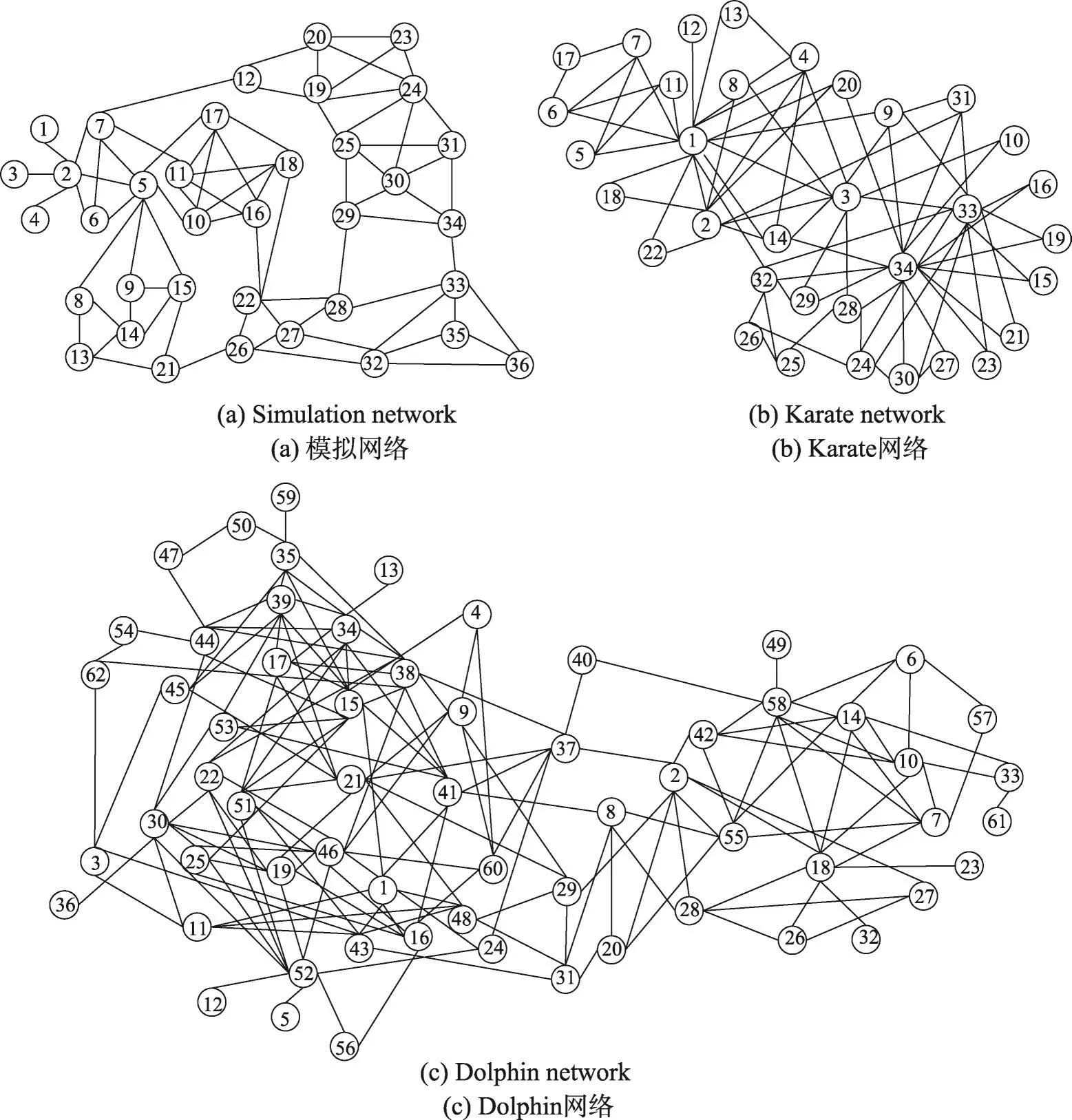
Fig.3 Social network圖3 社會網絡圖

在模擬網絡中，不同社區個數對應的模塊度值的大小變化曲線如圖4所示。因為各度量指標在VSFCM算法中形成的初始社區個數不同，所以各度量指標的模塊度曲線在圖6中的長短不同。在模擬網絡中，采用CN指標的網絡最大模塊度為0.624，劃分為6個社區，分別為（16，18，10，11，17，22）、（26，27，28，32，36，35，33）、（12，23，19，20，24）、（25，34，30，29，31）、（1，3，4，2，6，7，5）和（8，9，21，13，14，15）；采用RA指標的網絡最大模塊度為0.589，劃分為 6 個社區，分別為（3，1，4）、（18，16，11，10，17）、（34，25，30，31，29）、（20，19，24，23，12）、（33，32，36，35，27，22，28，26）和（6，2，14，5，7，13，15，21，8，9）；采用Katz指標的網絡最大模塊度為0.637，劃分為6個社區，分別為（1，2，3，4，6，7，5）、（8，13，14，21，9，15）、（16，18，10，11，17）、（20，23，19，24，12）、（30，31，34，29，25）和（35，36，32，33，26，27，22，28）；采用SPCD1指標的網絡最大模塊度為0.603，劃分為7個社區，分別為（16，18，17，10，11）、（35，36，32，33，26，27，22，28）、（30，31，29，34，25）、（1，3，4，2，6，7，5）、（8，13，14，21）、（9，15）和（12，20，23，24，19）；采用SPCD2指標的網絡最大模塊度為0.596，劃分為5個社區，分別為（5，7，4，2，6，1，3）、（8，9，21，13，14，15）、（16，18，10，11，17，19，20，12，23）、（22，27，33，26，28，32，35，36）和（24，25，34，29，31，30）；采用WCCD指標的網絡最大模塊度為0.637，劃分為6個社區，分別為（1，2，3，4，6，7，5）、（8，13，14，21，9，15）、（16，18，10，11，17）、（20，23，19，24，12）、（30，31，34，29，25）和（35，36，32，33，26，27，22，28）。由此可見，本文WCCD指標與全局性Katz指標具有最大的網絡模塊度值，優于其他4種局部度量指標；在不同社區劃分層次中，都取得了較大的模塊度值，并實現了社區的正確劃分。

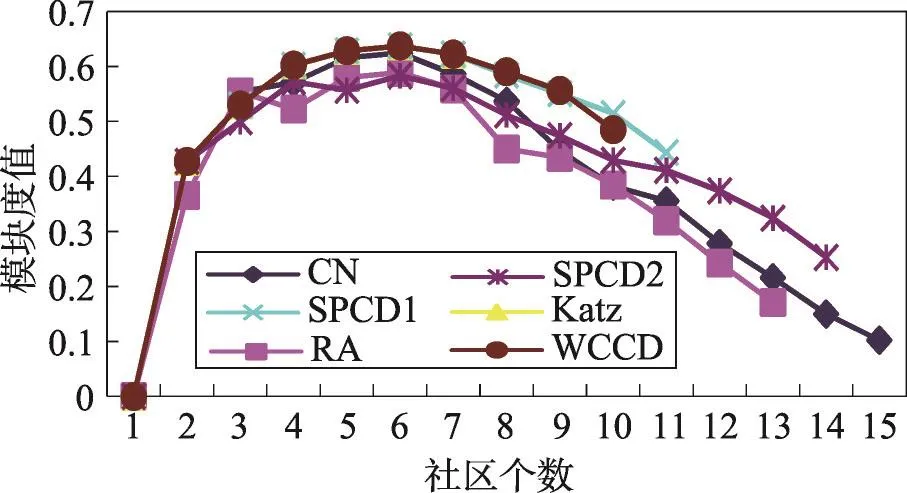
Fig.4 Experimental results of 6 indicators in simulation network圖4 6種指標在模擬網絡中的實驗結果

同樣，采用6種相似性度量指標，在Karate網絡和Dolphin網絡中進行社區劃分，不同社區個數對應的模塊度值的大小變化曲線如圖5、圖6所示；各度量指標的網絡最大模塊度值、社區個數對比情況如表1所示。通過對模塊度值大小的比較，采用本文WCCD度量指標進行社區劃分，均可得到最大的模塊度值；在不同的社區劃分層次中，也取得了較大的模塊度值，較好地體現了社區劃分結果。由此可見，WCCD指標接近甚至優于全局性Katz度量指標，明顯優于其他局部相似性度量指標，合理地刻畫了網絡中頂點間的關系值。

Fig.5 Experimental results of 6 indicators in Karate network圖5 6種指標在Karate網絡中的實驗結果

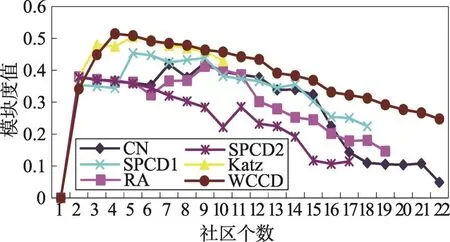
Fig.6 Experimental results of 6 indicators in Dolphin network圖6 6種指標在Dolphin網絡中的實驗結果

5.2 社區發現實驗分析

現有多種社區發現算法，主要分為基于分裂的方法，如GN算法[31]；基于模塊度的方法，如CNM算法[32]；基于標簽傳播的方法，如LP（label propagation）算法[33]；基于譜聚類的方法，如SC（spectral clustering）[34]等經典社區發現算法[35]。為了驗證基于WCCD相似性度量指標在VSFCM算法下社區劃分結構的優劣，在10種具有代表性的真實網絡中，與上述4種算法進行比較實驗。真實網絡包括：空手道俱樂部Karate網絡[30]、海豚Dolphin網絡[30]、美國大學足球聯賽FB網絡[30]、爵士音樂家合作Jazz網絡[36]、線蟲神經Neural網絡[30]、美國航空 USAir網絡[36]、電子郵件 Email網絡[30]、科學家合作NS網絡[30]、美國大選政治博客PB網絡[30]、美國電力PG網絡[30]。本文將全部數據集視為無向無權的二元網絡。研究表明，很多真實網絡中的頂點具有模塊性特征[37]，且真實網絡的社區發現比模擬網絡更具挑戰，不能事先預知其社區結構，因此只能采用模塊度進行比較。實驗結果如表2所示。

在表2中，第1列為真實網絡列表，第2列和第3列為網絡的基本統計數據（頂點數和邊數），第4至13列為5種社區發現算法，對每種算法統計了社區發現的最大模塊度值和社區數目。例如，在Karate網絡中，采用GN算法得出的最大模塊度值為0.401，劃分的社區數為5。考慮到具有較高復雜度的GN算法具有較好的社區劃分結果，因此在表2中取每個網絡模塊度值的前兩位，其中加粗數據表示最大值，加粗加下劃線表示次大值。由表2可見，從模塊度值角度比較，采用WCCD度量指標的VSFCM算法取得了7次領先，而采用全局性度量指標的GN算法取得了6次領先，尤其是在USAir網絡的社區發現中，GN算法和LP算法給出了接近0的模塊度值，而VSFCM算法仍取得了較好的社區結構效果；考慮模塊度增量作為社區劃分標準的CNM算法取得了5次領先，相對較好，而LP算法與SC算法表現較差，LP算法僅取得了1次領先，SC算法一次領先也沒有。從社區劃分數目角度比較，GN算法傾向于給出較多的社區劃分數目，例如PB網絡分為205個社區，顯著高于其他算法；此外LP和VSFCM為3個社區，較為接近真實的社區數目，其余方法給出的社區數均為10個以上，顯然相應的方法有過于擬合的傾向。

5種算法在數據集中的運行時間如圖7所示。在圖7中，橫坐標表示頂點數及真實網絡，縱坐標表示算法的運行時間。由圖7可知，隨著網絡中頂點數和邊數的增加，各個算法的運行時間顯著增長。總體來看，貪婪的CNM算法和LP算法運行速度較快，比較適合處理大型網絡。SC算法由于采用了ARPACK加速特征根的計算方法，隨著網絡規模的增加，運行時間增加緩慢。但LP算法和SC算法獲得的模塊度值偏低，其速度的增加是以社區劃分效果為代價的。消耗時間最多的是GN算法，該算法需要從全局角度計算邊界數。VSFCM算法的運行效率明顯優于GN算法，雖然遜于SC算法和LP算法，但社區劃分效果明顯優于SC算法和LP算法。

綜上，與其他4種算法相比，采用WCCD度量指標的社區發現算法VSFCM均取得了較大社區模塊度值，表明本文提出的WCCD相似性度量指標可以實現較好的社區劃分結果。

Table 2 Experimental results of 5 community discovering algorithms表2 5個算法社區劃分結果的比較

6 結束語

本文將社會網絡定義為一個同異反系統，針對網絡拓撲結構，基于聯系度刻畫分析了頂點間相似性，給出了基于加權聚集系數聯系度的頂點間相似性模型的表示及計算方法；進一步給出了網絡社區間相似性模型。為了進一步考察上述相似性度量指標的實際性能，將其應用于現有社會網絡數據集中實現社區發現，實驗結果顯示，基于本文提出的頂點間相似性度量指標可以正確和有效地實現社區發現。如何刻畫有向有權等更復雜網絡中頂點間的相似性，以及如何研究網絡動態演化是下一步的研究目標。

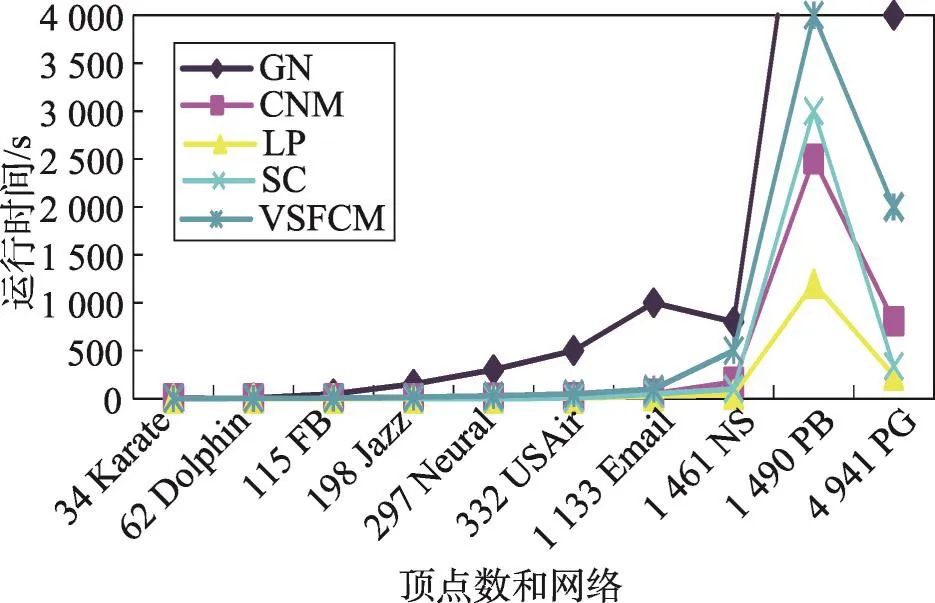
Fig.7 Comparison of vertices number and running time圖7 頂點數與運行時間對比圖

[1]Girvan M,Newman M E J.Community structure in social and biological networks[J].Proceedings of the National Academy of Sciences of the United States of America,2002,99(12):7821-7826.

[2]Lv Linyuan,Zhou Tao.Link prediction in complex networks:a survey[J].Physica A Statistical Mechanics&Its Applications,2011,390(6):1150-1170.

[3]Katz L.A new status index derived from sociometric analysis[J].Psychometrika,1953,18(1):39-43.

[4]Leicht E A,Holme P,Newman M E J.Vertex similarity in networks[J].Physical Review E,2006,73(2):026120.

[5]Fouss F,Pirotte A,Renders J,et al.Random-walk computation of similarities between nodes of a graph with application to collaborative recommendation[J].IEEE Transactions on Knowledge&Data Engineering,2007,19(3):355-369.

[6]G?bel F,Jagers A A.Random walks on graphs[J].Stochastic Processes&TheirApplications,1974,2:311-336.

[7]Brin S,Page L.The anatomy of a large-scale hypertextual Web search engine[J].Computer Networks&ISDN Systems,1998:107-117.

[8]Lorrain F,White H C.Structural equivalence of individuals in social networks[J].Journal of Mathematical Sociology,1971,1(1):49-80.

[9]Salton G,McGill M J.Introduction to modern information retrieval[M].New York:McGraw-Hill,1983.

[10]Hamers L,Hemeryck Y,Herweyers G,et al.Similarity measures in scientometric research:the Jaccard index versus Salton's cosine formula[J].Information Processing&Management,1989,25(89):315-318.

[11]Zhou Tao,Lv Linyuan,Zhan Yicheng.Predicting missing links via local information[J].The European Physical Journal B:Condensed Matter and Complex Systems,2009,71(4):623-630.

[12]Liu Weiping,Lv Linyuan.Link prediction based on local random walk[J].Europhysics Letters,2010,89(5):58007-58012.

[13]Bai Meng.Link prediction of complex network:the algorithm based on structure similarity[D].Xiangtan:Xiangtan University,2011.

[14]Chiang K Y,Natarajan N,Tewari A,et al.Exploiting longer cycles for link prediction in signed networks[C]//Proceedings of the 20th Conference on Information and Knowledge Management,Glasgow,UK,Oct 24-28,2011.New York:ACM,2011:1157-1162.

[15]Zhao Keqin.Set pair analysis and its preliminary application[M].Hangzhou:Zhejiang Science and Technology Press,2000.

[16]Zhang Chunying,Liang Ruitao,Liu Lu.Set pair social network analysis is model and its application[J].Journal of Hebei Polytechnic University:Natural Science Edition,2011,33(3):99-103.

[17]Zhang Chunying,Guo Jingfeng.The α relation communities of set pair social networks and its dynamic mining algorithms[J].Chinese Journal of Computers,2013,36(8):1682-1692.

[18]Zhang Chunying.Research on modeling and situation analysis theory of social network based on attribute graph[D].Qinhuangdao:Yanshan University,2013.

[19]Zhang Chunying,Guo Jingfeng.The attribute graph model of social networks and its application[M].Beijing:Beijing University of Posts and Telecommunications Press,2014:186-198.

[20]Zhao Chanyuan.The research on link prediction method in social network[D].Harbin:Harbin Engineering University,2012.

[21]Li Tao,Fu Qiang,Ding Hong.Research for variation coefficient in set pair analysis based on correlation degree of grey theory[J].Journal of Heilongjiang Hydraulic Engineering,2010,37(1):97-99.

[22]Esley D,Kleinberg J.Networks,crowds,and markets[M].Cambridge:Cambridge University Press,2010:49-50.

[23]Han Jiawei,Kamber M.Data mining:concepts and techniques[M].San Francisco,USA:Morgan Kaufmann Publishers Inc,2011:457-470.

[24]Newman M E J,Girvan M.Finding and evaluating community structure in networks[J].Physical Review E,2004,69(2):292-313.

[25]Fortunato S,Barthélemy M.Resolution limit in community detection[J].Proceedings of the National Academy of Sciences of the United States ofAmerica,2007,104(1):36-41.

[26]Zhang Jiali.The problem of modularity and its algorithm research in community detection[D].Shanghai:East China Normal University,2015.

[27]Jiang Shengyi,Yang Bohong,Wang Lianxi.An adaptive dynamic community detection algorithm based on incremental spectral clustering[J].Acta Automatica Sinica,2015,41(12):2017-2025.

[28]Li Huijia,Li Huiying,Li Aihua.Analysis of multi-scale stability in community structure[J].Chinese Journal of Computers,2015,38(2):301-311.

[29]Bhatia M P S,Gaur P.Statistical approach for community mining in social networks[C]//Proceedings of the 2008 International Conference on Service Operations&Logistics,&Informatics,Beijing,Oct 12-15,2008.Piscataway,USA:IEEE,2008:207-211.

[30]Newman M.Network datasets[EB/OL].[2016-05-21].http://www-personal.umich.edu/～mejn/netdata/.

[31]Newman M E J,Girvan M.Finding and evaluating community structure in networks[J].Physical Review E,2004,69(2):026113.

[32]Clauset A,Newman M E J,Moore C.Finding community structure in very large networks[J].Physical Review E,2004,70(6):066111.

[33]Raghavan U N,Albert R,Kumara S.Near linear time algorithm to detect community structures in large-scale networks[J].Physical Review E,2007,76(3):036106.

[34]Newman M E J.Finding community structure using the eigenvectors of matrices[J].Physical Review E,2006,74(3):036104.

[35]Jiang Shengyi,Yang Bohong,Li Minmin,et al.Overlapping community detection algorithm based on two-stage clustering[J].Pattern Recognition and Artificial Intelligence,2015,28(11):983-991.

[36]Batageli,Mrvar A.Pajek datasets[EB/OL].[2016-05-21].http://vlado.fmf.unilj.si/pub/networks/data/default.htm.

[37]Li Yafang,Jia Caiyan,Yu Jian.Survey on community detection algorithms using nonnegative matrix factorization model[J].Journal of Frontiers of Computer Science and Technology,2016,10(1):1-13.

附中文參考文獻:

[13]白萌.復雜網絡的鏈路預測:基于結構相似性的算法研究[D].湘潭:湘潭大學,2011.

[15]趙克勤.集對分析及其初步應用[M].杭州:浙江科學技術出版社,2000.

[16]張春英,梁瑞濤,劉璐.集對社會網絡圖分析模型及其應用[J].河北理工大學學報:自然科學版,2011,33(3):99-103.

[17]張春英,郭景峰.集對社會網絡α關系社區及動態挖掘算法[J].計算機學報,2013,36(8):1682-1692.

[18]張春英.基于屬性圖的社交網絡建模與態勢分析理論研究[D].秦皇島:燕山大學,2013.

[19]張春英,郭景峰.社交網絡屬性圖模型與應用[M].北京:北京郵電大學出版社,2014:186-198.

[20]趙嬋媛.一種社會網絡鏈接預測算法研究[D].哈爾濱:哈爾濱工程大學,2012.

[21]李陶,付強,丁紅.基于灰色關聯度的集對分析差異系數研究[J].黑龍江水專學報,2010,37(1):97-99.

[26]張家利.社區發現的模塊度問題及其算法研究[D].上海:華東師范大學,2015.

[27]蔣盛益,楊博泓,王連喜.一種基于增量式譜聚類的動態社區自適應發現算法[J].自動化學報,2015,41(12):2017-2025.

[28]李慧嘉,李慧穎,李愛華.多尺度的社團結構穩定性分析[J].計算機學報,2015,38(2):301-311.

[35]蔣盛益,楊博泓,李敏敏,等.基于二階段聚類的重疊社區發現算法[J].模式識別與人工智能,2015,28(11):983-991.

[37]李亞芳,賈彩燕,于劍.應用非負矩陣分解模型的社區發現方法綜述[J].計算機科學與探索,2016,10(1):1-13.

Measuring Similarity Between Vertices and ItsApplication in Social Network*

CHEN Xiao1,2,3,GUO Jingfeng1,3+,ZHANG Chunying4
1.College of Information Science and Engineering,Yanshan University,Qinhuangdao,Hebei 066004,China
2.College of Qian'an,North China University of Science and Technology,Qian’an,Hebei 064400,China
3.The Key Laboratory for Computer Virtual Technology and System Integration of Hebei Province,Qinhuangdao,Hebei 066004,China
4.College of Science,North China University of Science and Technology,Tangshan,Hebei 063009,China

A

TP391

+Corresponding author:E-mail:jfguo@ysu.edu.cn

CHEN Xiao,GUO Jingfeng,ZHANG Chunying.Measuring similarity between vertices and its application in social network.Journal of Frontiers of Computer Science and Technology,2017,11(10)：1629-1641.

ISSN 1673-9418 CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology

1673-9418/2017/11(10)-1629-13

10.3778/j.issn.1673-9418.1607025

E-mail:fcst@vip.163.com

http://www.ceaj.org

Tel:+86-10-89056056

*The National Natural Science Foundation of China under Grant No.61472340(國家自然科學基金);the National Youth Science Foundation of China under Grant No.61602401(國家青年科學基金項目);the Natural Science Foundation of Hebei Province under Grant Nos.F2017209070,F2016209344(河北省自然科學基金).

Received 2016-07,Accepted 2016-12.

CNKI網絡優先出版:2016-12-06,http://www.cnki.net/kcms/detail/11.5602.TP.20161206.1712.002.html

CHEN Xiao was born in 1983.She is a Ph.D.candidate at Yanshan University,a lecturer at North China University of Science and Technology,and the member of CCF.Her research interests include graph mining and social network analysis,etc.

陳曉（1983—），女，河北秦皇島人，燕山大學博士研究生，華北理工大學講師，CCF會員，主要研究領域為圖挖掘，社會網絡分析等。發表學術論文20余篇。

GUO Jingfeng was born in 1962.He received the Ph.D.degree from Yanshan University in 2002.Now he is a professor and Ph.D.supervisor at Yanshan University,and the senior member of CCF.His research interests include database theory and application,data mining and social network analysis,etc.

郭景峰（1962—），男，黑龍江哈爾濱人，2002年于燕山大學獲得博士學位，現為燕山大學教授，CCF高級會員，主要研究領域為數據理論應用，數據挖掘，社會網絡分析等。發表學術論文100余篇，主持國家自然科學基金項目2項，省級科研項目3項。

ZHANG Chunying was born in 1968.She received the Ph.D.degree from Yanshan University in 2013.Now she is a professor at North China University of Science and Technology,and the senior member of CCF.Her research interests include data mining and social network analysis,etc.

張春英（1968—），女，河北唐山人，2013年于燕山大學獲得博士學位，現為華北理工大學教授，CCF高級會員，主要研究領域為數據挖掘，社會網絡分析等。發表學術論文30余篇，主持省級科研項目1項。