一種改進的譜聚類方法在復雜網絡社團檢測中的應用

王 林，閆安文

(西安理工大學 自動化與信息工程學院，陜西 西安 710048)

一種改進的譜聚類方法在復雜網絡社團檢測中的應用

王 林，閆安文

(西安理工大學 自動化與信息工程學院，陜西 西安 710048)

社團結構是復雜網絡的重要特征之一。譜聚類方法在復雜網絡社團檢測中具有十分重要的作用。針對譜聚類算法在復雜網絡社團檢測中只選擇部分特征向量聚類的問題，提出了一種改進的譜聚類方法，該方法對網絡矩陣的所有特征向量進行加權，并引入尺度參數，采用網絡矩陣的所有特征向量進行聚類。實驗結果表明，與傳統譜聚類算法相比，該方法可以有效地對網絡進行劃分，并可以反映出網絡中社團的多尺度特性。

復雜網絡；社團檢測；模塊度；譜圖方法

Abstract: Community structure is one of important features of complex network. Spectral clustering methods take important position in the community detection in complex networks. Aiming at the issue that just a part of eigenvectors are used to cluster in the community detection, an improved spectral clustering method is proposed, in which all eigenvectors are weighted, scale parameter is involved and all eigenvectors are used to cluster. Experiment results indicate that, compared with traditional spectral clustering methods, not only community structures can be efficiently detected, but multi-scale feature of community can be reflected.

Key words:complex network; community detection; modularity; spectral graph method

0 引言

現實生活中許多復雜系統都可以抽象為復雜網絡。隨著對復雜網絡的深入研究，人們發現許多實際網絡都具有一些共同的拓撲特性，如小世界特性、無標度特性以及社團結構。由于復雜網絡的社團結構性質對于研究基礎設施網絡、生物網絡、經濟與社會網絡具有十分重要的意義[1]，因而受到了國內外許多學者的廣泛關注。

針對復雜網絡中社團的劃分問題，研究者從不同角度出發，提出了復雜網絡中社團檢測算法。該算法主要分為三類：基于模塊度的方法[2-4]、基于統計推理的方法[5]和譜方法[6-8]。從模塊度優化問題出發，NEWMAN M E在文獻[2]中根據模塊度矩陣的最大特征值所對應的特征向量迭代地將網絡二分化，直到模塊度取得最大值，模塊度貪婪優化算法通過將網絡中的節點看作獨立的社團，通過迭代地合并節點并計算對應的模塊度，直到模塊度不再取得更大值；從統計推理的角度出發，人們發現可以通過網絡的結構信息擬合出一個塊模型，基于此，文獻[5]中提出了用于社團檢測的度矯正隨機塊模型；由于譜聚類算法易于實現、更加高效并且聚類效果好，因此，許多學者從譜聚類的角度提出了復雜網絡社團劃分方法。然而，由于譜聚類算法通常只選擇網絡矩陣的部分特征向量進行聚類，并沒有充分考慮到網絡的全局拓撲結構。

為了改善譜聚類算法在社團檢測中的上述缺點，本文提出了一種改進的譜聚類方法，該方法通過對網絡矩陣的所有特征向量加權，考慮到了網絡的全局拓撲結構，并引入尺度參數，還可反映出網絡中社團的多尺度特性。

1 圖傅里葉變換

類似于傳統傅里葉變換積分求和的概念，HAMMOND D K等人[9]將圖Laplace矩陣的特征向量作為頻率分量，Laplace矩陣的特征值作為頻譜，給出了向量圖傅里變換的定義，并引入了譜圖小波變換的概念。

1.1網絡Laplace矩陣

對于含有N個節點的無向無權網絡G=(V,E)，V=(v1,v2,…,vN)為網絡的節點集，E為網絡的邊集。設網絡的鄰接矩陣為A，則其元素aij表示為：

(1)

考慮網絡的無向性，有aij=aji，即矩陣A為實對稱矩陣。

設節點i的度為d(i)，可以發現:

d(i)=∑jaij

(2)

網絡Laplace矩陣定義為:L=D-A，其中D=diag(d(1),d(2),…,d(N))為對角矩陣。Laplace矩陣L為實對稱矩陣，其最小特征值λ1=0，該值的重數為網絡的連通分支數，考慮全連通網絡，其特征值可排列為：0=λ1<λ2≤…≤λN，假設特征值所對應的特征向量分別為：χ1，χ2，… ，χN，由于矩陣L的實對稱特性，對其特征向量作規范化處理后，不難發現不同的特征向量相互正交，并且χ1=(1,1,…,1)T。設矩陣χ=[χ1,χ2,…,χN]，可以發現該矩陣的不同列之間相互正交，并且χ與其轉置矩陣χT互為逆矩陣，即χχT=χTχ=I,其中I為N階單位矩陣。

1.2網絡節點的圖小波表示

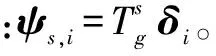
2 方法原理

現有的譜聚類方法只選擇網絡矩陣的部分特征向量進行聚類，希望可以采用網絡的全部特征向量進行聚類。如前文所述網絡Laplace矩陣的零特征值對應的特征向量χ1在所有節點上的分量均為1，無法將節點區分開，而χN又過分地將節點區分開(在極端情況下，每個節點被劃分為獨立的社團)，因此，考慮對特征向量進行加權，加權函數g(x)應當在χ1上為0，而在較高頻率分量處衰減。可以認為網絡Laplace矩陣的小波基為網絡節點在歐式空間中的一種映射，這樣網絡節點的聚類問題就可轉化為矩陣ψs中行元素的余弦相似性問題。

2.1加權函數

為了使加權函數具有前文所述性質，并能取得較好的局部化效果，采用文獻[10]中明確指定的g(x)定義以及尺度區間：

(3)

根據對應的網絡Laplace矩陣，計算其最小非零特征值λ2以及最大特征值λN，尺度參數區間設置為：[smin,smax]，其中smin=2/λN，smax=2/λ2。

2.2尺度參數

不同的網絡對應的Laplace矩陣不同，為了使加權函數能適用于不同的網絡，引入尺度參數s，s的值受網絡Laplace矩陣特征值的約束，這樣，選擇合適的尺度，當前網絡矩陣的特征向量便可取得較好的加權效果。

當尺度參數s選擇較小值時，如01)時，加權函數g(sx)則處于壓縮狀態，只有部分低頻分量被加權，網絡劃分的社團個數較少，節點的聚類效果則相對粗糙。實際上，可以認為尺度參數s反映了網絡中節點的連接情況，s值越大，以某節點為中心，其鄰居節點越多。s=0.5和s=2時的加權函數曲線如圖1所示。

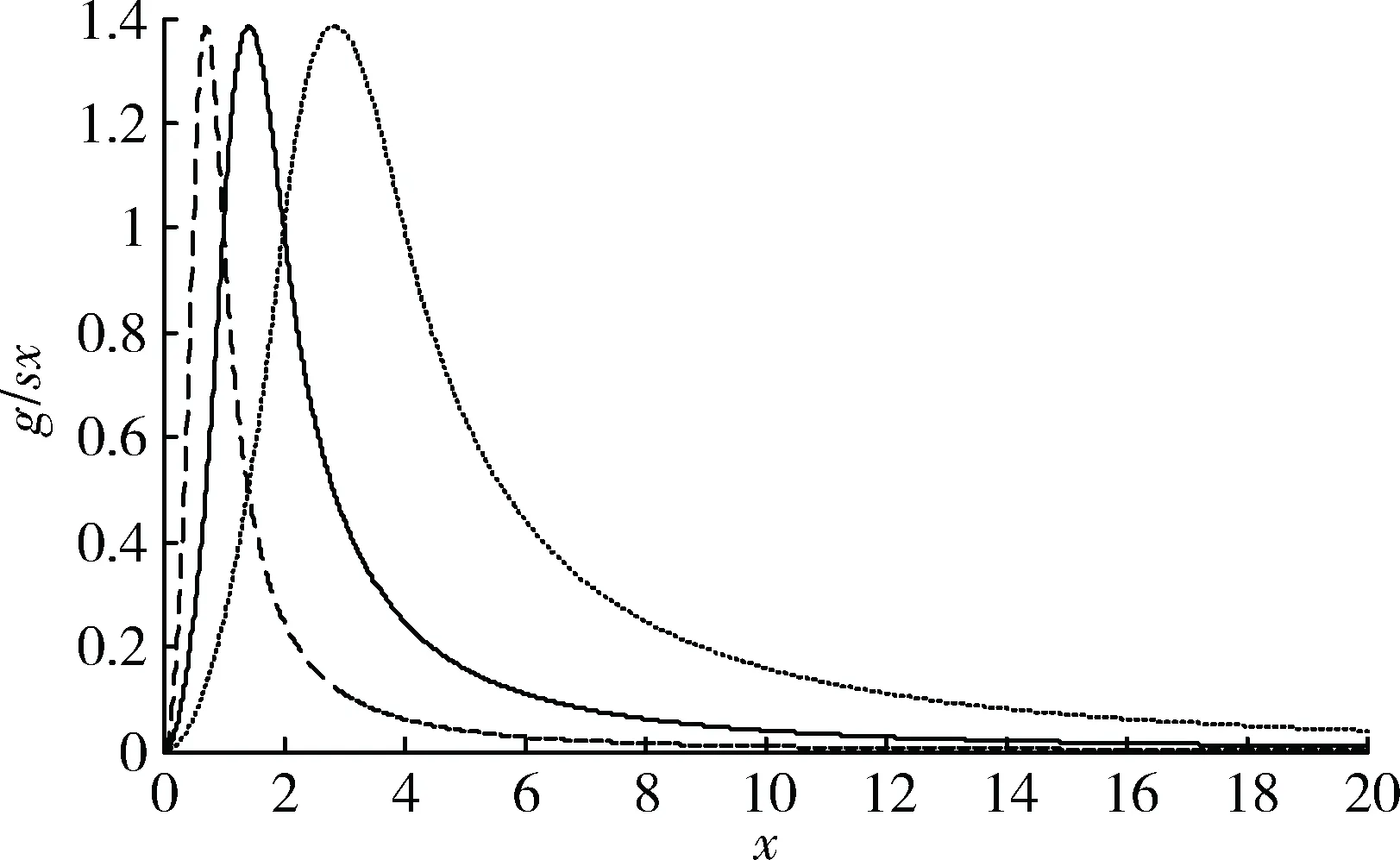
圖1 加權函數g(x) (實線)，s=0.5時(點線)，s=2時(虛線)

3 結果分析

通過四個實際網絡來測試本文算法：Zachary網絡[11]，Jazz網絡[10]，E-mail網絡[12]，物理學家(Physicists)合作網絡[13]。

根據Zachary網絡矩陣的最小非零特征值λ2以及最大特征值λN的估計值，設置尺度參數s∈[0.1, 4.2]，當尺度參數s=4.2時，網絡被劃分為兩個社團，如圖2所示。

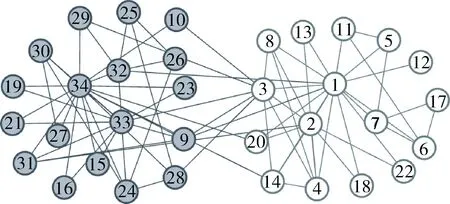
圖2 Zachary網絡在尺度參數s=4.2時的劃分情況

通過設置不同的尺度參數，發現Zachary網絡在尺度參數s=4.2時，網絡得到了正確劃分。通過設置不同的尺度參數，這四個實際網絡的最大模塊度Q值，對比經典社團劃分算法：GN算法[2]、CNM算法[4]、DA算法[3]如表1所示。

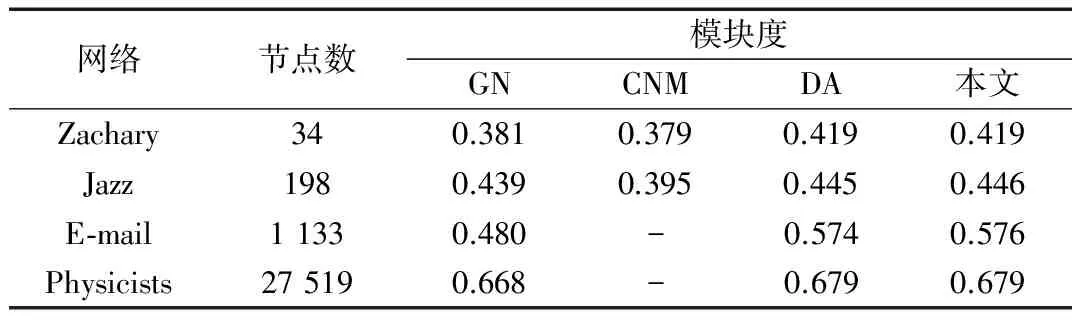
表1 本文方法與經典社團劃分算法的Q值對比

實驗結果表明，通過選擇合適的尺度參數以及加權函數，復雜網絡中的社團結構能夠得到較好的劃分。

4 結論

在譜聚類算法的基礎上，本文從譜圖小波變換的角度對傳統的譜聚類算法進行的改進：對網絡矩陣的所有特征向量進行加權，并利用所有特征向量進行聚類，充分考慮了網絡的全局拓撲結構，另外引入了尺度參數的概念，可以有效地反映網絡的多尺度特性。由于尺度參數取離散的對數化間隔，是否存在更佳的尺度參數值以及加權函數可使得網絡得到更優的劃分還在研究之中，另外該方法的缺陷在于網絡矩陣的特征向量的計算復雜度較高。

[1] 汪小帆,汪秉宏,曹進德,等.復雜網絡的結構功能性質及其應用[J].系統工程理論與實踐, 2008,28(5): 45-48.

[2] NEWMAN M E. Modularity and community structure in networks[J]. Proceedings of the National Academy of Sciences, 2006, 103(103):8577-82.

[3] DUCH J, ARENAS A. Community detection in complex networks using extremal optimization[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2005, 72(2):986-1023.

[4] CLAUSET A, NEWMAN M E, MOORE C. Finding community structure in very large networks[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2010, 70(6 Pt 2):264-277.

[5] KARRER B, NEWMAN M E J. Stochastic blockmodels and community structure in networks[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2011,83(1pt2): 016107.

[6] WHITE S, SMYTH P. A spectral clustering approach to finding communities in graph[C]. Siam International Conference on Data Mining, 2005: 274-285.

[7] NEWMAN M E. Spectral methods for community detection and graph partitioning.[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2013, 88(4):330-337.

[8] Shen Huawei, Cheng Xueqi. Spectral methods for the detection of network community structure: a comparative analysis[J]. Computer Science, 2010,2010(10):10020.

[9] HAMMOND D K, VANDERGHEYNST P, GRIBONVAL R. Wavelets on graphs via spectral graph theory[J]. Applied & Computational Harmonic Analysis, 2009, 30(2):129-150.

[10] GLEISER P, DANON L. Community structure in Jazz[J]. Advances in Complex Systems, 2003(6): 565-573.

[11] ZACHARY W W. An information flow model for conflict and fission in small groups[J]. Journal of Anthropological Research, 1977, 33(4): 452-473.

[12] EBEL H, MIELSCH L I, BORNHOLDT S. Scale-free topology of e-mail networks.[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2002, 66(3):035103.

[13] NEWMAN M E J. The structure of scientific collaboration networks[C]. Proceedings of the National Academy of Sciences of the United States of America, 2001, 98(2):404-409.

An improved spectral clusteringmethod used in community detection of complex network

Wang Lin, Yan Anwen

(School of Automation and Information Engineering, Xi’an University of Technology, Xi’an 710048, China)

TN929.12

A

10.19358/j.issn.1674- 7720.2017.18.009

王林，閆安文.一種改進的譜聚類方法在復雜網絡社團檢測中的應用[J].微型機與應用，2017,36(18)：30-31，35.

2017-03-22)

王林(1963-)，男，博士，教授，主要研究方向：復雜網絡、數據挖掘、大數據分析。

閆安文(1991-)，通信作者，男，碩士，主要研究方向：復雜網絡。E-mail：anvinvip@163.com。