高動態下GPS信號跟蹤環路的仿真研究

王麗黎，孫文鵬

(西安理工大學 自動化與信息工程學院，陜西 西安 710048)

高動態下GPS信號跟蹤環路的仿真研究

王麗黎，孫文鵬

(西安理工大學 自動化與信息工程學院，陜西 西安 710048)

GPS信號跟蹤過程是GPS接收機的核心組成部分，它是將捕獲階段得到的各項參數進行精確估計的過程，實現本地生成信號與輸入信號的準確同步。以高動態環境為前提，模擬生成GPS信號，改變衛星信號的加加速度，模擬高動態下所引起的多普勒頻移，分別使用傳統跟蹤環路與擴展卡爾曼濾波環路對信號進行跟蹤。仿真結果顯示，擴展卡爾曼濾波跟蹤環路更加穩定，精度有所提高。

高動態；GPS信號跟蹤；卡爾曼濾波

Abstract: The GPS signal tracking process is the core component of the GPS receiver. It is the process of accurately estimating the parameters obtained in the capture phase. It realizes the accurate synchronization of the local generated signal and the input signal. Based on the premise of high dynamic environment, this paper simulates the generation of GPS signals, changes the acceleration of satellite signals, simulates the Doppler shift caused by high dynamic motion, and uses the traditional tracking loop and the extended Kalman filter loop tracking signal respectively. The simulation results show that the extended Kalman filter tracking loop is more stable and the accuracy is improved.

Key words:high dynamic; GPS signal tracking; extended Kalman filter

0 引言

全球定位系統(GPS)是基于人造衛星的面向全球的全天候、高精度的定位和定時系統，在軍民領域均具有廣闊的用途和發展前景[1-2]。跟蹤模塊作為GPS接收機的核心部分，直接影響接收機的動態性、精度等性能指標。捕獲階段是對當前衛星信號載波頻率和碼相位的粗略估計，跟蹤環路則逐步精細對這兩個信號參量的估計，同時輸出對信號的各種GPS測量值，并且解調出信號中的導航電文數據比特。在高動態的環境下，會導致載波上附加大的多普勒頻移，導致載波跟蹤環容易失鎖，跟蹤將不能正常進行。若為了跟蹤到信號而加大跟蹤環路帶寬，這樣又使得跟蹤環路中的噪聲加強，影響跟蹤精度。

卡爾曼濾波器是目前應用最廣泛的狀態估計方法之一，其最大的優點是采用遞歸的方法來解決線性濾波的問題[3]。本文在詳細分析卡爾曼濾波的基本原理的基礎上，將擴展卡爾曼濾波器應用于GPS信號的跟蹤環路中，實現在高動態下跟蹤環路的正常進行，確保跟蹤精度，為GPS信號解算定位做好準備。

1 高動態運動對GPS信號的影響

1.1高動態下的多普勒頻移

在高動態的環境下，導航接收機與高速運動的GPS衛星之間存在著徑向移動，由此就會產生多普勒頻移，此時L1波段載波到達接收機時的頻率不再等于其發射頻率(1 575.42 MHz)，而是在此頻率上另加了一個多普勒頻移，使得接收信號的中心頻率產生偏移。

根據多普勒定律，多普勒頻移計算公式如下：

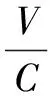
(1)

式中C表示光速，V表示衛星和載體間的相對速度，fL1表示GPS L1波段的載波頻率，其值為1 575.42 MHz。載體的運動一般由速度、加速度、加加速度三個因素構成，此處相對速度V可表示為：

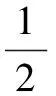
(2)

其中，vo表示初始速度，a、b分別表示加速度和加加速度。將式(2)帶入式(1)，得到由衛星和載體之間的相對運動速度造成的載波多普勒頻率值：

(3)

高動態運動造成載波多普勒頻率增大且變化劇烈，從而導致載波跟蹤環路失鎖。高動態運動對碼環中多普勒頻率影響相對較小，只有載波的1/1 540，可通過載波輔助消除，所以，研究載波跟蹤算法是GPS信號跟蹤的核心，也是解決高動態的問題的關鍵。

1.2高動態下的GPS信號

在MATLAB環境下進行高動態軌跡模擬[4]，其模型為一直向西的變加速直線運動，如圖1所示，通過改變加速度的大小，來調整多普勒頻移的大小。圖1(a)表示隨著時間的變化，衛星加加速度也一直在變；圖1(b)表示衛星的加速度；圖1(c)表示衛星的運動速度，速度最快達到2 000 m/s；圖1(d)表示運動所引起的多普勒頻率，最大達到8 000 Hz。

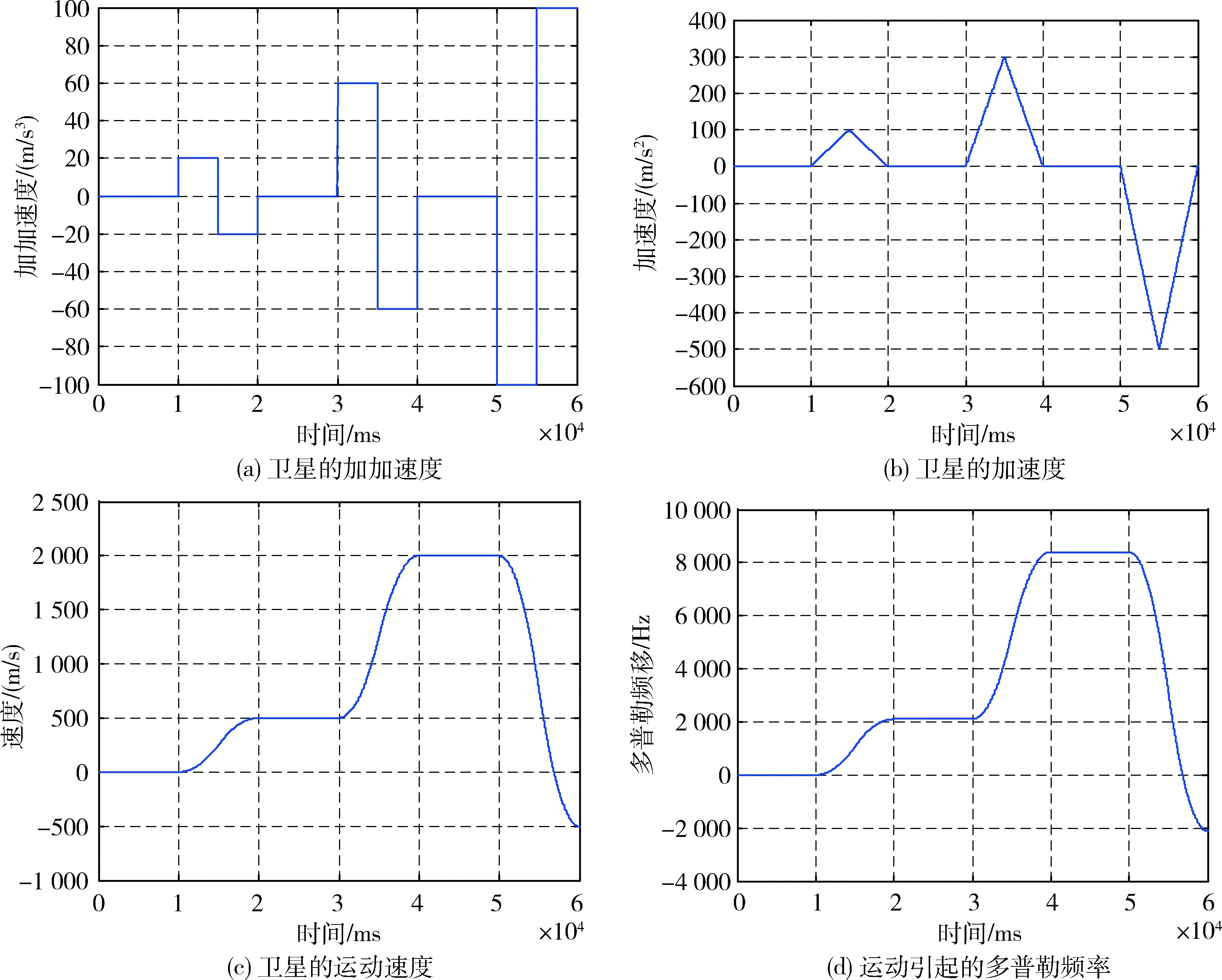
圖1 變加速直線運動模型

模擬的GPS信號模型[5]可表示為：

(4)

D(τ)=d[τj-ts(τj)]

(5)

C(τ)=C[τj-ts(τj)]

(6)

式中yj代表在τj時刻接收到的第j顆衛星的中頻信號；Pr表示接收信號的功率；D(τ)表示的是數據碼為50 Hz的導航電文調制；C(τ)表示1.023 MHz的C/A碼；ωIF表示接收到的載波中頻角頻率；ωd表示的是接收機與衛星間的多普勒頻移；φ0表示載波的初始相位值；nj表示高斯白噪聲。設定載波中頻為1.25 MHz，C/A碼為速率為1.023 MHz基碼/秒的偽隨機碼，D碼為50 Hz的數據。三種信號使用二進制相移鍵控(BPSK)調制。

2 GPS信號的跟蹤環路

2.1傳統跟蹤環路的原理

接收機的傳統跟蹤環路[6]的跟蹤算法一般是采用二階鎖頻環輔助三階鎖相環的組合環(FLL/PLL)，如圖2所示。

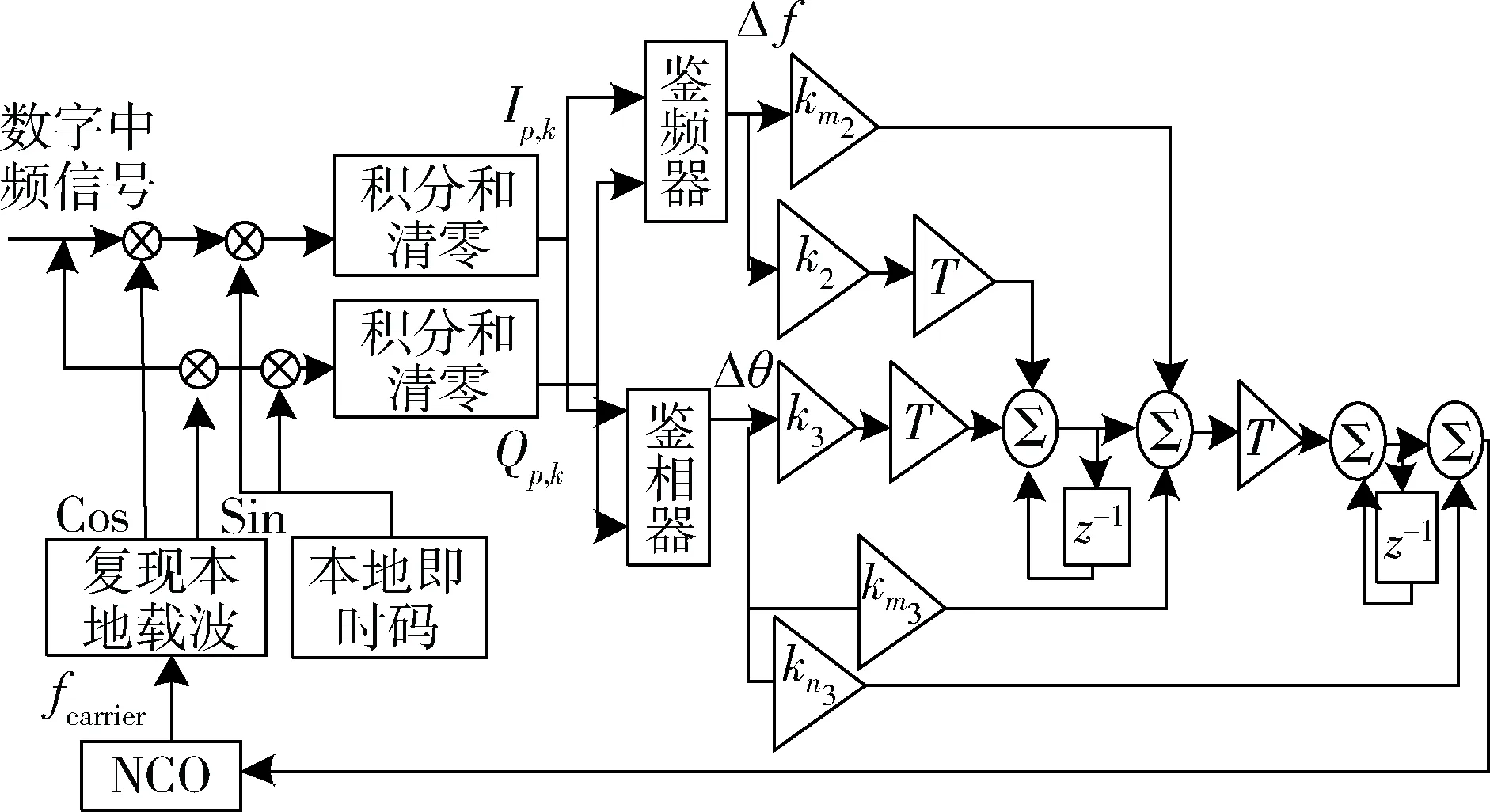
圖2 二階鎖頻環輔助三階鎖相環結構框圖

如圖2所示，二階FLL和三階PLL的濾波器分別使用一階矩形濾波器和二階矩形濾波器，環路的計算公式如下：

s0=s0+(Δθ·k3+Δf·k2)·T

(7)

s1=s1+(Δθ·km3+s0+Δf·km2)·T

(8)

fd=s1+kn3·Δθ

(9)

fcarrier=fref+fd

(10)

其中，Δθ為鑒相器的輸出值，Δf為鑒頻器的輸出值，fcarrier為通過復合環路進行更新后的本地信號載波頻率。

2.2卡爾曼濾波的原理

假設某個離散時間系統的狀態方程和觀測方程[7]為：

(11)

式中xk為n×1狀態向量，φ為n×n狀態轉移矩陣，uk-1為系統輸入向量，ηk-1為n×1系統狀態噪聲向量，zk為m×1觀測向量，H為n×m觀測矩陣，nk為m×1觀測噪聲矩陣。假設系統狀態噪聲{ηk}和觀測噪聲{nk}是相互獨立的零均值白噪聲序列。則得到；

(12)

其中Qk為系統狀態噪聲{ηk}的方差矩陣，Rk為觀測噪聲{nk}的協方差矩陣。

卡爾曼濾波過程如下：

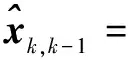
(13)

Pk,k-1=φPk-1φT+Qk-1

(14)

Kk=Pk,k-1HT(HPk,k-1HT+Rk)-1

(15)

(16)

Pk=(I-KkH)Pk,k-1

(17)

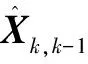
2.3擴展卡爾曼濾波器的原理

在實際情況下，系統模型通常是非線性的，經典的線性卡爾曼濾波器已不能使用，可用擴展卡爾曼濾波器(EKF)，其狀態方程和觀測方程為：

(18)

其中，f(·)為狀態向量xk關于上一時刻狀態向量xk-1的非線性函數；h(·)為觀測向量zk關于狀態向量xk的非線性函數。當噪聲nk和ηk為零時，式(19)所對應的系統模型即“預測參考狀態”，記為：

(19)

得到非線性系統的真實狀態與預測參考狀態的誤差為：

(20)

如果這兩個誤差足夠小，則可以將式(19)進行泰勒展開式，并取一階近似值，得到：

δxk-1+ηk-1

(21)

(22)

將式(19)帶入式(21)和式(22)中，得到：

(23)

(24)

綜合上式得到離散型非線性系統的線性誤差方程得：

(25)

(26)

其中φk為狀態誤差轉移矩陣：

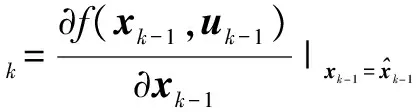
(27)

Hk為觀測矩陣：

(28)

2.4擴展卡爾曼濾波器的系統模型

擴展卡爾曼濾波器的載波算法結構如圖3所示。

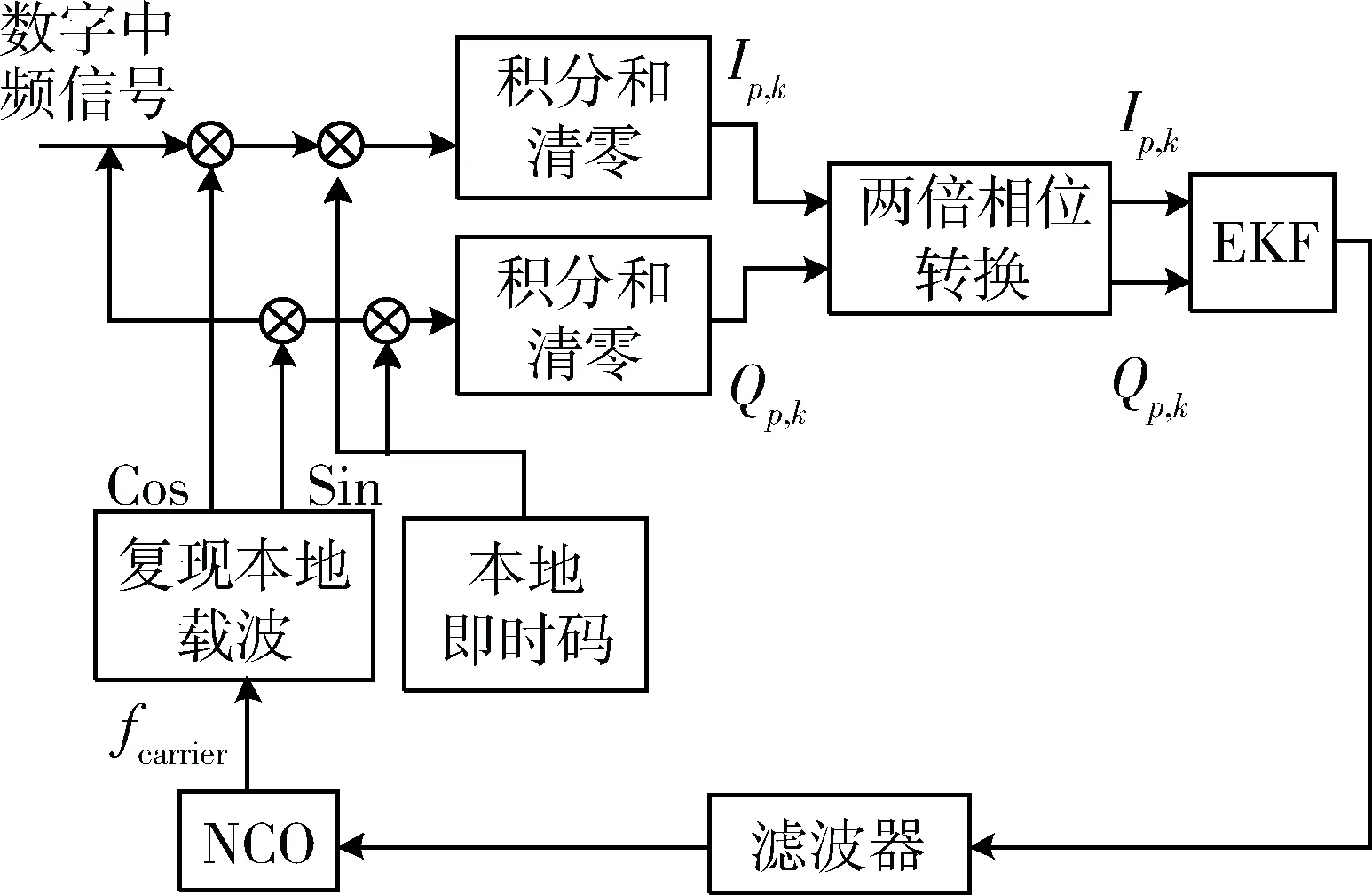
圖3 EKF跟蹤算法結構框圖

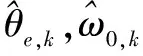
(29)

其中T為預檢積分時間，ηi,k-1為系統噪聲。EKF觀測方程為:

(30)

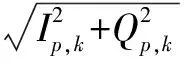
3 仿真結果

跟蹤測試時，傳統跟蹤環路中設置預檢測積分為1 ms，PLL噪聲帶寬為80 Hz，DLL噪聲帶寬10 Hz，通過仿真得到載波多普勒頻移跟蹤結果如圖4所示，載波相位差如圖5所示，其均方誤差11.2°，偽距誤差如圖6所示，其均方差為12.5 m。

圖4 傳統跟蹤環路得到的多普勒頻率

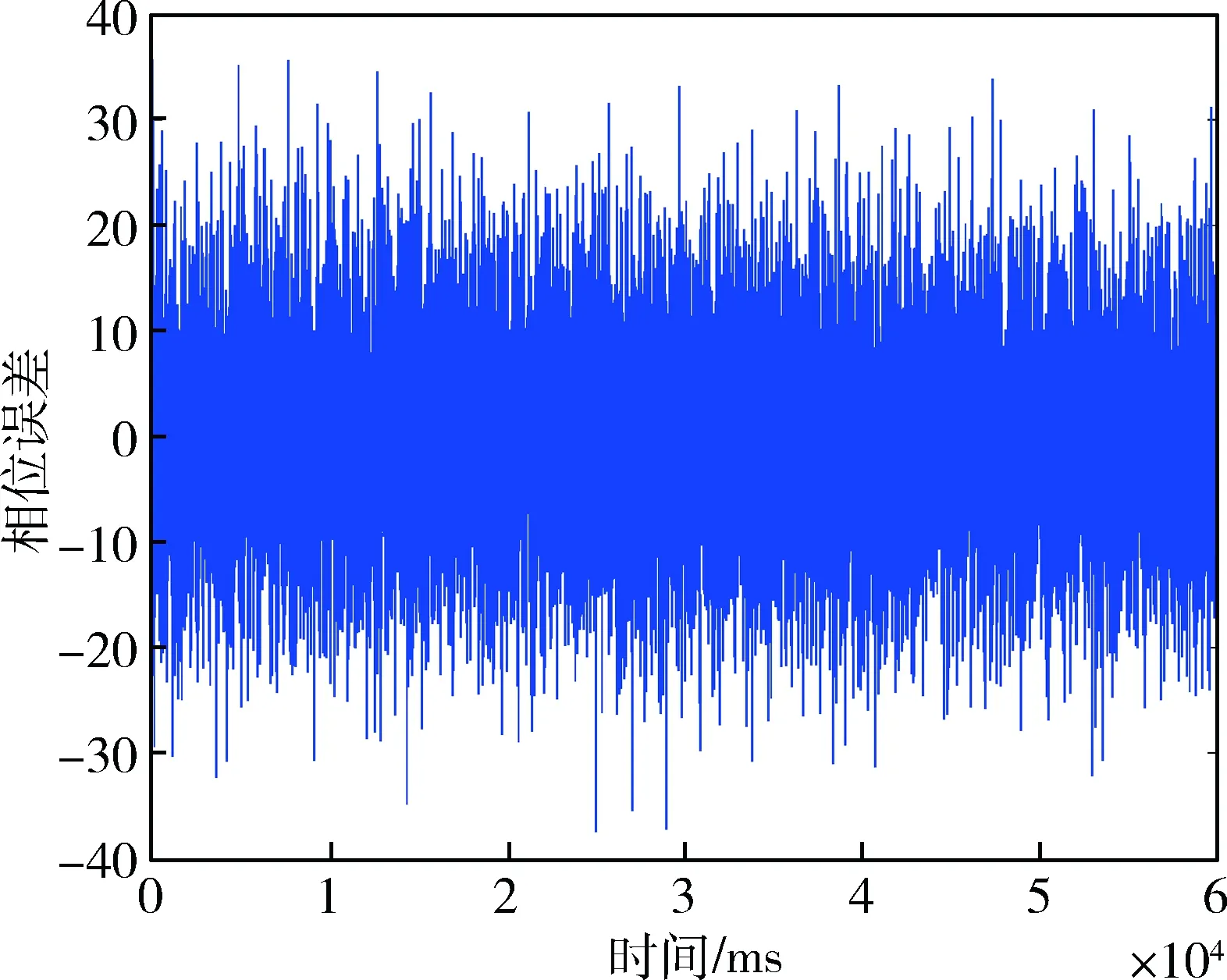
圖5 傳統跟蹤環路的載波相位誤差

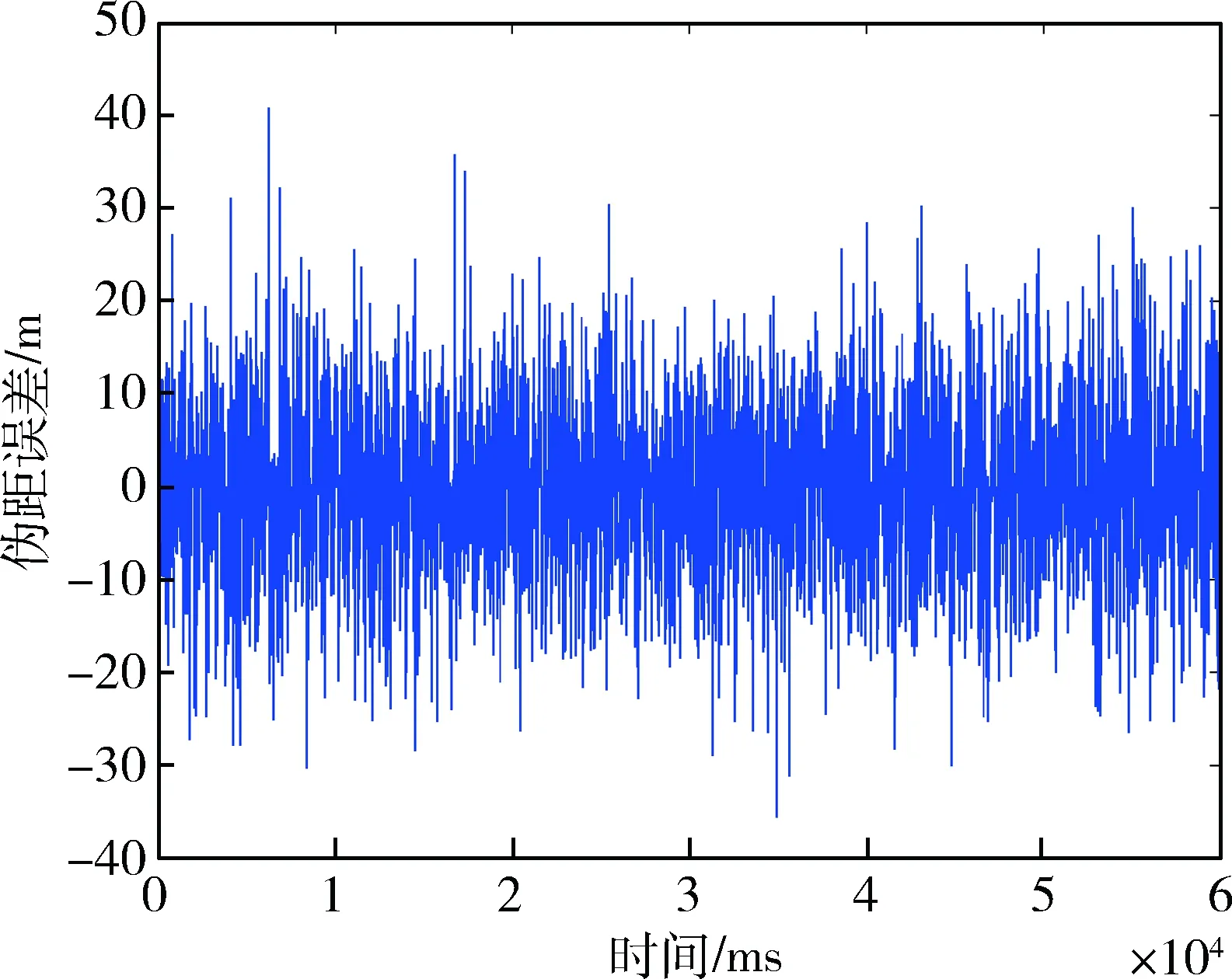
圖6 傳統跟蹤環路的偽距誤差

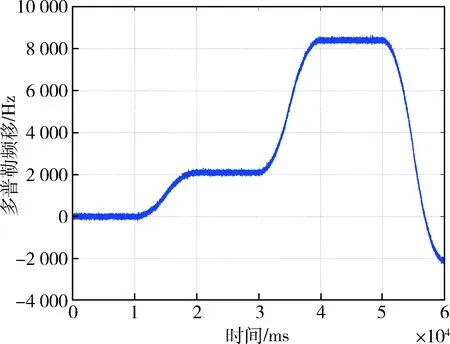
圖7 EKF跟蹤環路得到的多普勒頻率

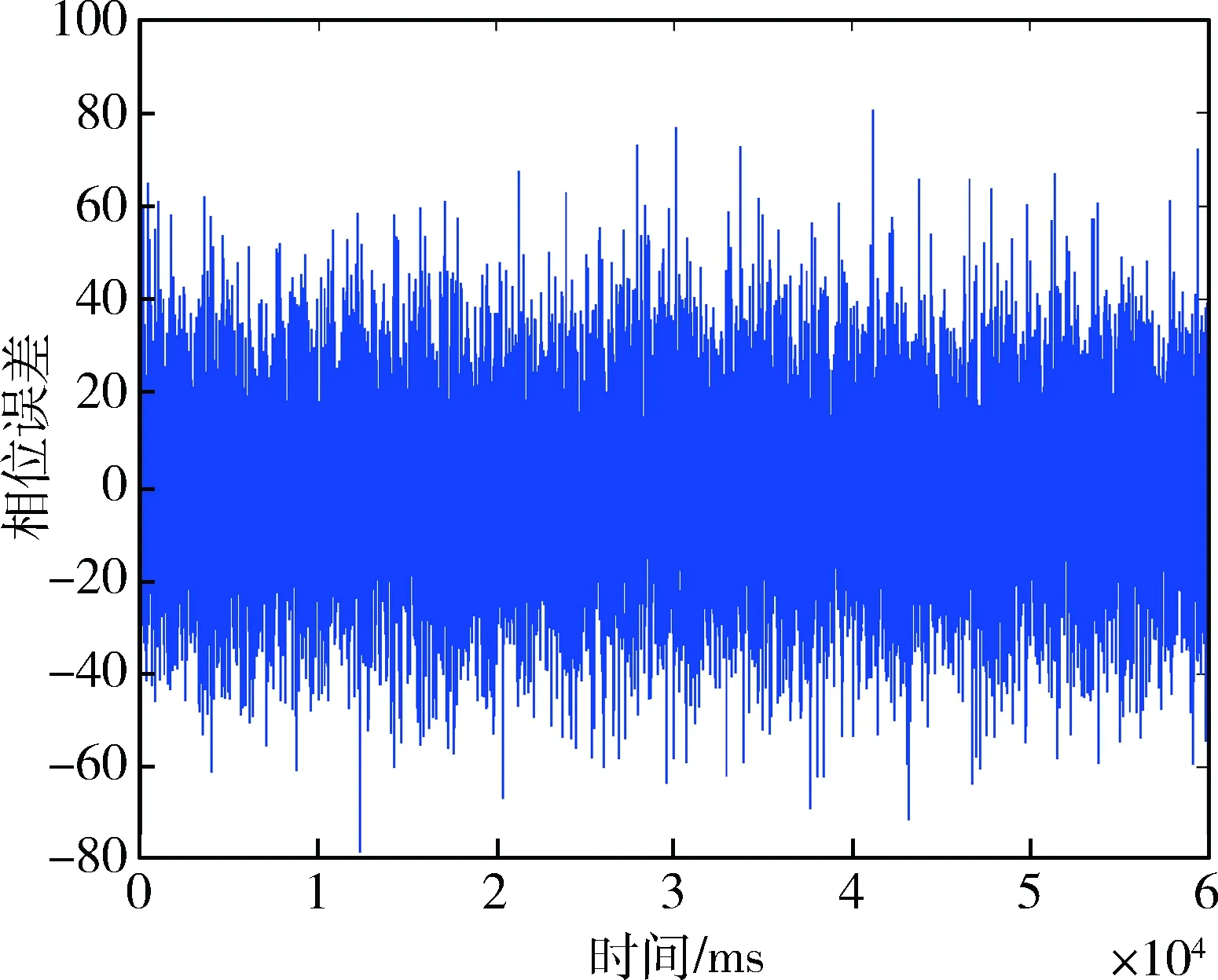
圖8 EKF仿真跟蹤過程中的載波相位誤差

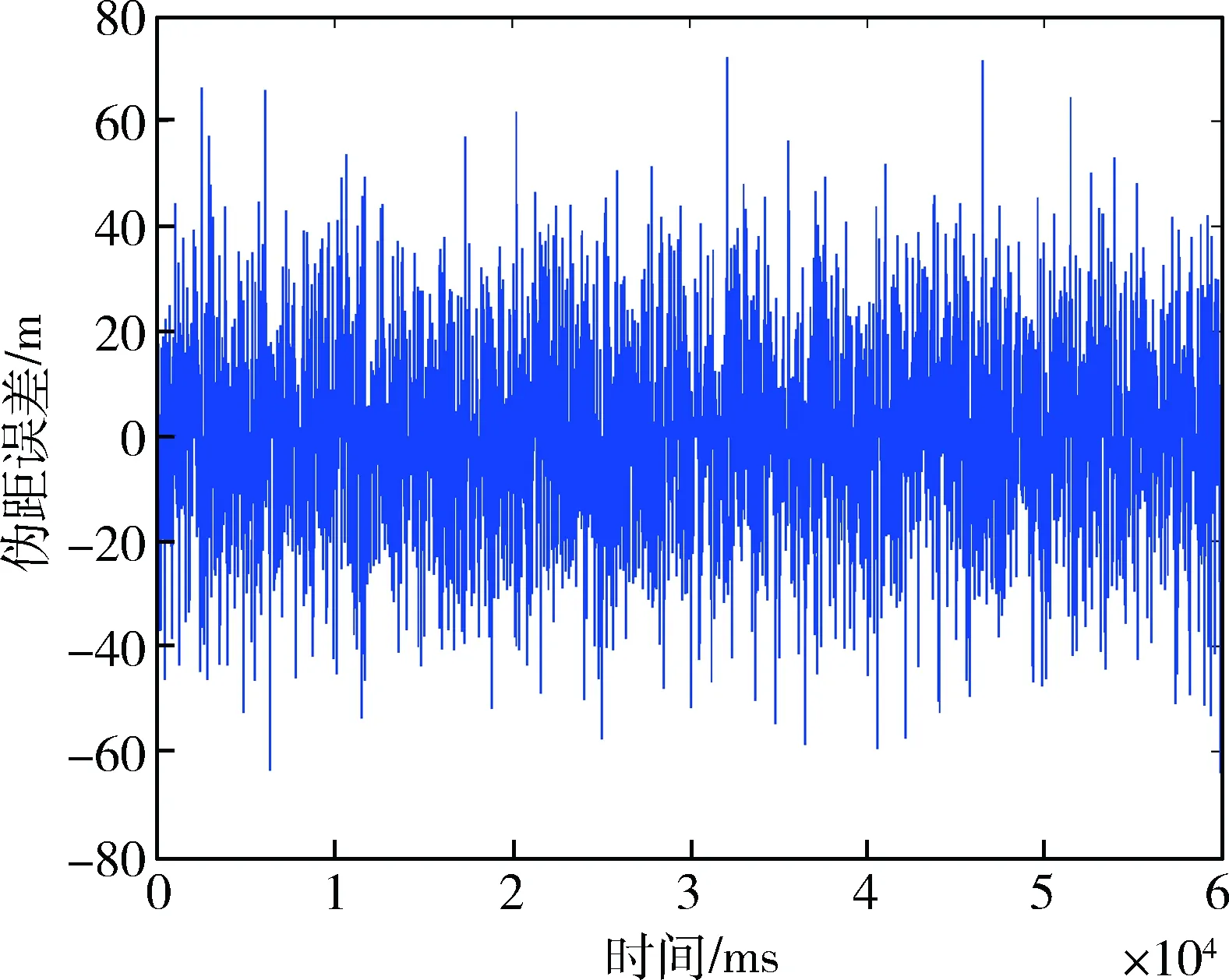
圖9 EKF仿真跟蹤過程中的偽距誤差

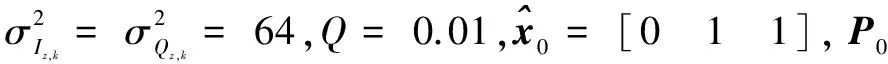
4 結論

仿真結果表明，在高動態中，傳統跟蹤環路在提高動態性能和提高測量精度兩個方面是存在矛盾的，較寬的環路噪聲帶寬頻率使捕獲帶更大，有助于信號的跟蹤，但此時的測量精度也會變差。擴展卡爾曼濾波跟蹤環路應用觀測新值不斷對系統噪聲和觀測噪聲進行遞推與更新，具有較快的收斂性和較強的自適應性，還保持了較高的精度。

應用擴展卡爾曼濾波技術的GPS信號跟蹤環路優于傳統的跟蹤環路。擴展卡爾曼濾波技術能夠實現高動態跟蹤技術跟蹤穩定，而且精度有所提高。

[1] 毛亞青,胡展鵬,俞嘯,等.基于車載GPS終端的城市環境健康監測平臺設計[J].電子技術應用,2016,42(5):68-70.

[2] 徐偉,李智,王勇軍.北斗/GPS無人飛行器動態導航中改進自適應算法[J].電子技術應用,2015,41(10):58-61.

[3] 費恒敏,施琴,田俊杰.INS/GPS緊耦合組合導航系統抗差定位算法[J].微型機與應用，2015,34(7):20-23.

[4] 楊俊,武奇生. GPS基本原理及其Matlab仿真[M].西安:西安電子科技大學出版社,2006.

[5] 孟繁智.高動態GPS衛星信號模擬源的關鍵技術研究[D].長沙:國防科學技術大學,2004.

[6] 謝剛. GPS原理與接收機設計[M].北京:電子工業出版社,2009.

[7] 左啟耀,袁洪,林寶軍,等.基于Kalman濾波理論的高動態GPS信號跟蹤系統仿真研究[J].系統仿真學報,2009,21(8):2160-2164.

[8] 張雪麗.基于卡爾曼濾波的高動態GPS載波跟蹤算法研究[D].南昌:華東交通大學,2015.

Simulation of high dynamic GPS signal tracking loop

Wang Lili, Sun Wenpeng

(Faculty of Automation and Information Engineering, Xi’an University of Technology, Xi’an 710048, China)

TN961

A

10.19358/j.issn.1674- 7720.2017.18.020

王麗黎，孫文鵬.高動態下GPS信號跟蹤環路的仿真研究[J].微型機與應用，2017,36(18)：66-69，72.

2017-03-17)

王麗黎(1968-)，女，副教授，碩士生導師，主要研究方向：電磁波傳播、天線和智能天線。

孫文鵬(1990-)，男，碩士研究生，主要研究方向：先進導航中的信息處理。