基于核相似度支持向量數據描述的間歇過程監測

王建林，馬琳鈺，劉偉旻，邱科鵬，于濤

?

基于核相似度支持向量數據描述的間歇過程監測

王建林，馬琳鈺，劉偉旻，邱科鵬，于濤

（北京化工大學信息科學與技術學院，北京 100029）

基于支持向量數據描述的間歇過程監測方法選擇歷史過程數據中最大的核距離作為控制限，忽略了高維空間中超球體的不規則性，導致基于該方法的過程監測精度不高。針對上述問題，提出了一種基于核相似度支持向量數據描述的間歇過程監測方法，將間歇過程數據待監測樣本與支持向量之間的核函數值作為相似度權重，利用該相似度對不同時刻的支持向量球心距加權求和，得到待監測間歇過程數據樣本的動態控制限，通過判斷待監測樣本的球心距是否超過其動態控制限，實現間歇過程監測。所提方法綜合考慮了超球體的不規則性和過程數據在高維空間分布的局部特性，以及間歇過程數據待監測樣本的時變性，提高了間歇過程監測的準確性。利用數值仿真實驗和半導體金屬刻蝕實驗驗證了該方法的有效性。

核相似度；支持向量數據描述；動態監測；間歇過程

引 言

間歇過程作為工業生產中的一種重要生產方式，具有生產靈活、產品附加值高等特點，廣泛應用于食品、精細化工、生物制藥、金屬加工等領域[1-3]。間歇過程生產中出現異常，會直接降低產品質量，造成經濟損失，甚至會引發安全事故，因此，對間歇過程實施過程監測，能夠有效保障間歇過程安全生產、可靠運行，提高產品質量[4-5]。

數據驅動的多元統計間歇過程監測方法通過獲取單一或多個監測量在時間維度上的變化，并設定控制限，監測量超過控制限則認為過程發生了異常[6-11]。MPCA[12]（multiway principal component analysis）、MPLS[13]（multiway partial least squares）、MICA[14]（multiway independent component analysis）等方法均側重間歇過程數據的多批次特性，基于變量投影分解原理實現過程監測；針對大多數間歇過程具有的多時段特性，相繼出現了sub-PCA[15]、基于時段的PLS[16]等方法。然而，這些基于PCA與PLS的間歇過程監測方法需假設過程變量為正態分布且變量間線性相關，若過程數據結構較為復雜，不滿足上述假設，這些方法的有效性及過程監測精度會受到影響[17-19]。對于間歇過程數據的非線性特性，核函數被引入到過程監測方法中，如MKPCA[20]（multiway kernel PCA）與MKPLS[21]（multiway kernel PLS）方法，利用核函數將非線性過程數據嵌入特征空間，使其在特征空間中呈現線性關系，然而這類方法的控制限設定仍需假設變量服從高斯分布，制約了間歇過程監測精度的提升。

支持向量數據描述（support vector data description，SVDD）是一種有效的數據描述和處理方法，通過非線性變換將正常數據樣本空間映射到高維樣本空間，實現對數據的分類，已在間歇過程監測中得到應用。Sun等[22]提出了一種基于核距離多變量控制圖的過程監測方法（kernel-distance- based multivariate control chart, K chart），該方法對過程數據分布不作假設，且不要求變量間線性相關，克服了傳統過程監測方法的缺陷。但是該方法選擇了歷史過程數據中最大的核距離作為異常判定閥值，未考慮高維空間中超球體的不規則性以及過程數據在高維空間分布的局部特性，因此降低了間歇過程監測精度。Camci等[23]提出一種啟發式參數選擇方法，通過優化核函數的超參數來調節K chart方法的控制限；Ning等[24]在此基礎上，同時考慮多個參數對控制限的影響，實現對控制限的優化設置。然而，上述基于參數優化方法的控制限沿用了支持向量的最大球心距，未考慮局部數據對超球結構的影響，忽略了超球體的不規整性。針對該問題，Sukchotrat等[25]提出基于支持向量球心距排序的控制限設計方法，通過權衡樣本誤分率與超球半徑大小，選擇滿足給定排序比例的超球半徑均值作為異常控制限，獲得了更為合理的監測控制限；Khediri等[26]在確定控制限時引入了可接受性參數，用以涵蓋訓練樣本未能表達的部分數據，實現控制限的有效性修正。但這兩種方法均引入了新的設定參數，對監測效果影響較大，也未給出參數選擇方法，使其應用受到限制。

提出了一種基于核相似度SVDD的間歇過程監測方法，使用正常工況下獲取的間歇過程數據作為訓練樣本，采用SVDD構造包含訓練樣本的最小超球體，將待監測樣本與支持向量之間的核函數值作為相似度權重，利用該相似度對不同時刻的支持向量球心距加權求和，得到待監測間歇過程數據樣本的動態控制限，通過判斷待監測樣本的球心距是否超過其動態控制限，實現間歇過程監測。

1 基于SVDD的過程監測

1.1 支持向量數據描述（SVDD）

SVDD是由Tax和Duin[27]提出的一種數據描述與處理方法，其核心是在高維空間中構造包含被描述對象的最小體積封閉超球。

給定訓練數據集∈R,=1,2,…,，構造包含的超球體轉化為如式(1)的最優化問題。

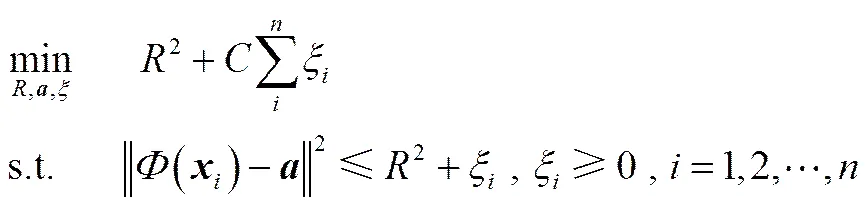
其中，與分別是超球體的球心和半徑；和ξ分別為懲罰系數和松弛因子，是針對訓練樣本中可能含有的離群點而引入的參數。

式(2)為式(1)最優化問題的對偶形式；引入式(3)所示的高斯核函數能夠簡化內積運算，完成特征空間映射；懲罰系數的參考值如式(4)所示，其中為訓練樣本處于超球體外部的百分比，為訓練樣本總數，通過參數可以協調球體體積與訓練樣本誤分率。式(2)～式(4)中，α為Lagrange乘子，為核函數，為高斯核函數寬度參數。

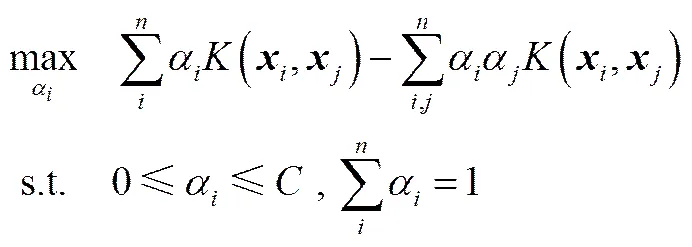
(3)

(4)

對應的Lagrange乘子滿足0<α<的為處于球體表面的支持向量，對滿足該條件的支持向量索引進行篩選，組成整數集合；由式(5)計算支持向量超球球心距，即超球體的半徑，其中為任一支持向量，∈。

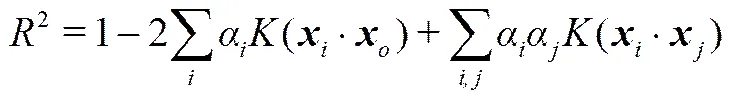
利用式(6)計算測試樣本到球體中心的距離，當該距離小于或等于球體半徑時認為測試樣本與訓練樣本為同一類數據。

(6)

SVDD對數據沒有高斯分布、相互獨立或呈線性關系的要求，適用范圍較廣[28-29]；其球形分類邊界能夠實現更高階的數據邊界描述。同時，SVDD中測試樣本與中心的距離是一種有效的監控量，距離越大說明點發生異常的可能性越大。

1.2 基于SVDD的過程監測

基于SVDD的過程監測方法利用正常過程數據構造訓練樣本，讀入待監測過程數據作為測試樣本；使用支持向量∈s替代訓練樣本簡化原算式，簡化后的測試樣本核距離kd計算式如(7)，若該距離小于最大的支持向量球心距m，則認為該過程點正常，判別條件如式(8)。

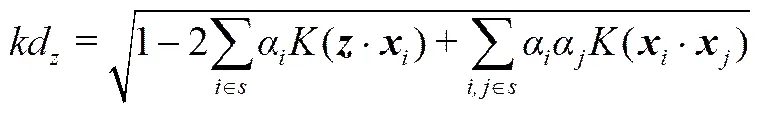
(8)

基于SVDD的過程監測方法能夠處理高維、非線性過程數據，不要求過程數據服從高斯分布，相比傳統方法能夠提高過程監測水平。但是，對于不同支持向量計算所得的不同球心距，該方法選擇了最大的支持向量球心距作為控制限，沒有考慮高維空間中超球體的不規則性，以及過程數據在高維空間分布的局部特性和待監測過程數據樣本的時變性，限制了該方法的應用范圍。

2 基于核相似度SVDD的間歇過程監測

2.1 核相似度SVDD

由于高維空間中超球形狀的不規則性，各支持向量對應的超球半徑各不相同，現有的基于SVDD的控制限設置方法忽略了這種不規則性，將所有支持向量對應的超球半徑取均值或最大值，作為類別劃分邊界。對于不同子集之間數據特性差異較大的數據集，這類固定的控制限無法兼顧到不同局部的特性，因此導致較多的誤判；另外，當數據集具有時變特性，固定的控制限無法適應其數值特征隨時間的變化，同樣會出現較多誤判。因此，本研究提出核相似度SVDD方法，根據測試樣本在高維空間中與支持向量的位置相似性，設定針對于該測試樣本的判別控制限。

過程數據到特征空間的投影是通過核函數完成的，向量之間的核函數值能夠度量兩個向量間的相似性。選擇測試樣本與支持向量∈s間的核函數值作為相似性的度量量，核相似度權重kel的定義式如(9)所示，由式(10)對核相似度權重進行標準化處理，獲得核相似度權值kel，為控制限的選擇提供依據，其中為支持向量個數。

(10)

由式(11)計算得到測試樣本對應的判別限，即每個支持向量的球心距與測試樣本的核相似度加權求和，得到的動態監測邊界R，式中T表示的轉秩，為支持向量球心距集合，如式(12)所示，R為∈s中第個支持向量的球心距，計算如式(13)所示。

(12)

(13)

對比式(7)獲得的測試樣本球心距kd和上述計算所得的動態監測邊界R，由式(14)判斷該樣本點的核距離是否超出了該點對應的動態判別限。當滿足式(14)時，則判斷樣本點的數據類型不同于訓練數據集。

kd>z(14)

核相似度SVDD改進了控制限的計算方式，其訓練樣本計算量與SVDD相同，獲取動態監測邊界R時不增加訓練樣本的計算量；對過程數據在高維空間分布的局部特性和支持向量球心距造成的不規則性，通過核函數量化測試樣本與支持向量間的比鄰關系，動態調整各支持向量球心距的權重作為局部控制限的計算依據；采用測試樣本參與自身控制限計算，使得控制限能夠反映測試樣本的時變性。

2.2 基于核相似度SVDD的間歇過程監測

核相似度SVDD同時考慮了超球模型的局部特征和測試樣本的特性，建立的動態異常判別閾值能夠自動適應數據特性的變化，實現間歇過程監測。圖1為基于核相似度SVDD的間歇過程監測流程圖。

基于核相似度SVDD的間歇過程監測實現步驟如下：

（1）在正常工況的間歇過程中，采集多批次過程數據X(××)，為批次數，為每批次采樣長度，為監測變量個數。將多個批次的過程數據沿變量方向展開，得到新的二維數據矩陣(×) = {1×,=1,2,…,}，并將作為訓練樣本。求解包含訓練樣本的最小體積超球，得到支持向量集合及其對應的Lagrange乘子α，進而計算每個支持向量所對應的超球球心距R。

（2）讀入待監測間歇過程數據，構造測試樣本，與單個訓練數據樣本具有相同的監測變量個數。由式(6)計算的球心距kd。

（3）計算測試樣本與各支持向量∈之間的核函數值kel，作為控制限的權重，并進行標準化處理，得到核相似度權重kel。將標準化的權重與支持向量球心距加權求和，得到待監測樣本所對應的監測動態邊界閥值R。

（4）對比待監測樣本球心距kd與動態監測閥值R，若待監測樣本球心距超過閥值，即判定該過程點存在異常。

3 實驗驗證

3.1 數值仿真

采用如下人工數據集[30]對具有時段特性的批次過程進行異常監測，該過程如式(15)所示，分P1、P2兩個階段。式中，為批次編號，為樣本點數，3個過程變量1、2、3由服從均值分布的隨機變量生成，在第1、2階段的分布區間分別為[0.01, 2]和[1.5, 4]，1、2、3是均值為零、方差為0.01的高斯噪聲變量。訓練樣本均使用正常過程數據。

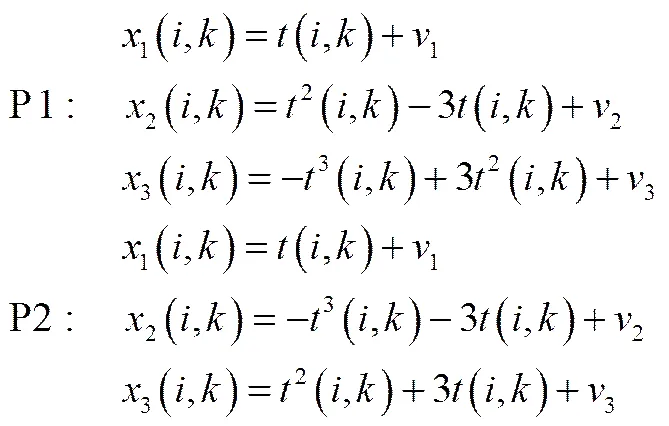
在上述過程中引入異常點生成測試樣本如式(16)，其中為單批次樣本點總數，設定均為偶數。

(16)

隨機生成5組數據，每組的訓練樣本含10個正常批次、每批次200個樣本點；每組的測試樣本為單批次、長度2000點。表1給出監測結果，其中Avg、Max和Dyn分別代表支持向量球心距均值、K chart和本文方法的誤分率（error rate），其計算公式如式(17)，代表錯誤分類的測試實例個數占測試實例總數的比例，其中FN（false negative）為被錯誤分類的負例個數，即故障樣本漏報個數；FP（false positive）為被錯誤分類的正例個數，即正常樣本的誤報個數，為樣本總數。表1最后兩列為誤分率均值與標準差。本文方法在不同的參數設定下有更小的誤分率均值與標準差，監測精度得到明顯提升，且監測效果受參數選擇情況的波動較小，性能更穩定。

error rate = (FN+FP)/(17)

圖2給出了參數設定=2、=0.4下，第1組數據data1的監測結果圖，其中DIS為測試樣本球心距，-dynamic、-average和-max分別為本文方法、支持向量球心距均值和K chart方法的控制限。可以明顯看出球心距均值與K chart方法在一定程度上對異常敏感，但無法兼顧每個階段的數據特性，產生較多漏報或者誤報，而本文方法定義的動態邊界能夠很好地描述不同階段訓練樣本的局部特征，并結合被測樣本的時變性，做到自動判別測試樣本的階段屬性，進而給出更加合理的動態控制限，監測效果更佳。

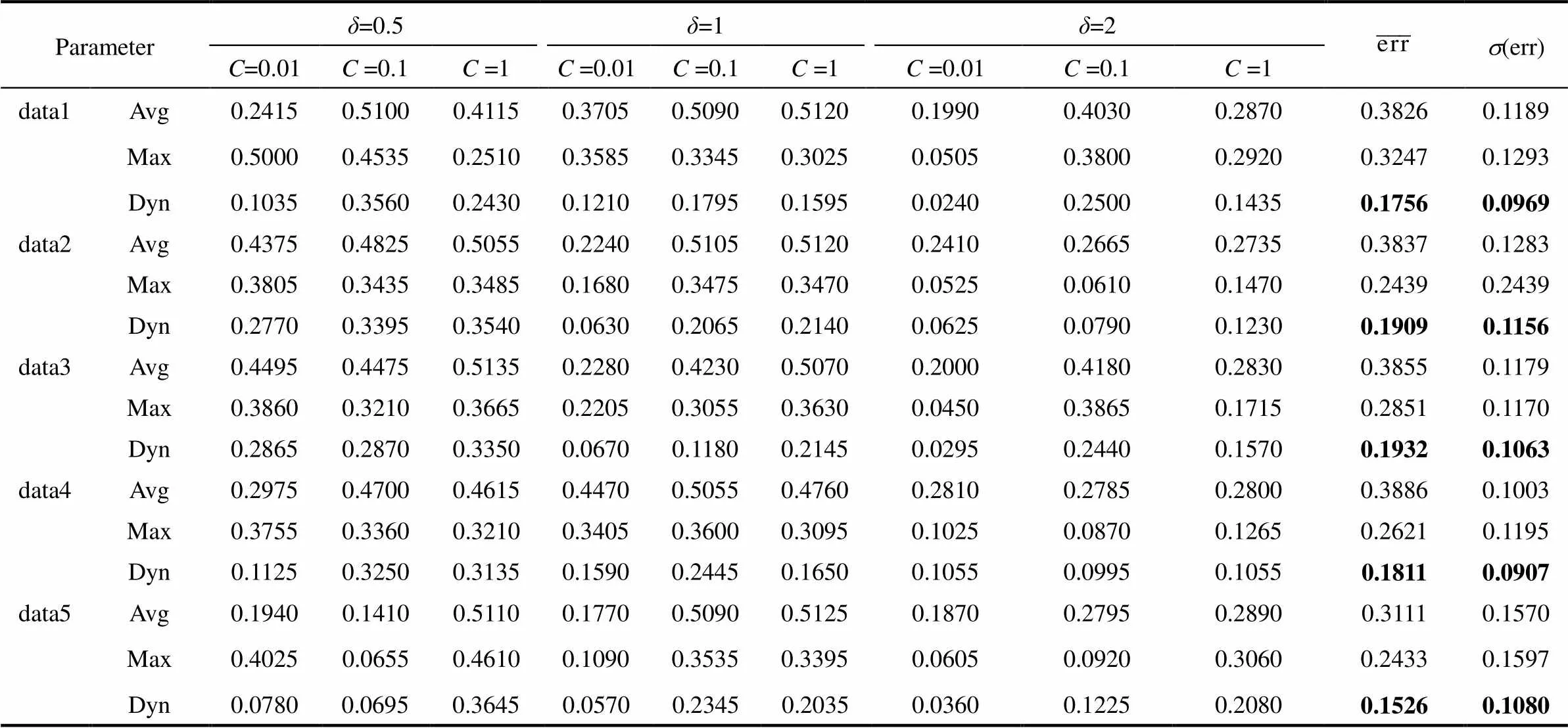
表1 不同樣本在不同實驗條件下的誤分率與誤分率標準差

3.2 半導體金屬刻蝕工業過程

蝕刻過程是半導體制造工藝的重要環節之一，是一個典型的非線性多時段和多工況的間歇過程。Lam9600TCP金屬蝕刻機[31]的過程數據由108個正常晶片和21個故障晶片構成，一個晶片制作過程為一個批次，共129批次數據。該數據集來自不同的3個實驗，分為系列L29、L31、L33，數據有著不同均值和一定差異的協方差結構。數據集每個點記錄了21個變量，變量含義見表2。在同樣的實驗條件下引入人為故障，共生成21個故障批次，故障描述見表3。由于該數據集正常批次第56批次和故障批次的第12批次明顯存在數據缺失，故剔除不用。

表2 半導體金屬刻蝕過程變量編號及名稱

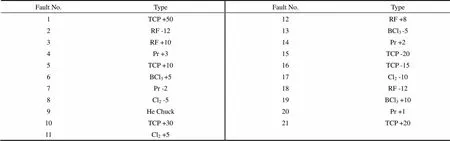
表3 金屬刻蝕過程故障批次編號及故障設定

隨機選擇30個正常批次作為訓練樣本，選擇19個監控變量作為單個樣本點輸入，對20個故障批次進行監測。設定誤分率=0.1，根據所選的訓練樣本長度=3037，由式(4)得到＝0.0033。選擇核函數參數=0.005。在上述固定參數設定下進行監測，表4給出了3種方法對20個故障批次的檢測率，圖3、圖4分別給出了故障批次5和故障批次19的監測結果圖。

由于半導體金屬刻蝕過程單批次數據在不同時段的特性差異較大，支持向量球心距均值與核距離控制圖難以在整個批次長度上都取得良好的監測效果，這兩種方法均在過程后半程出現較多的漏報，同時，這兩種控制限為不同批次提供數值相等的控制限，無法感知批次間的差異，因此監測精度較低。相比之下，本文方法獲得的動態控制限能夠很好地適應待監測樣本的特性，無論是批次間還是批次內，都能對待監測樣本點的球心距進行跟蹤，在整個批次過程中都能保持較好的監測結果。

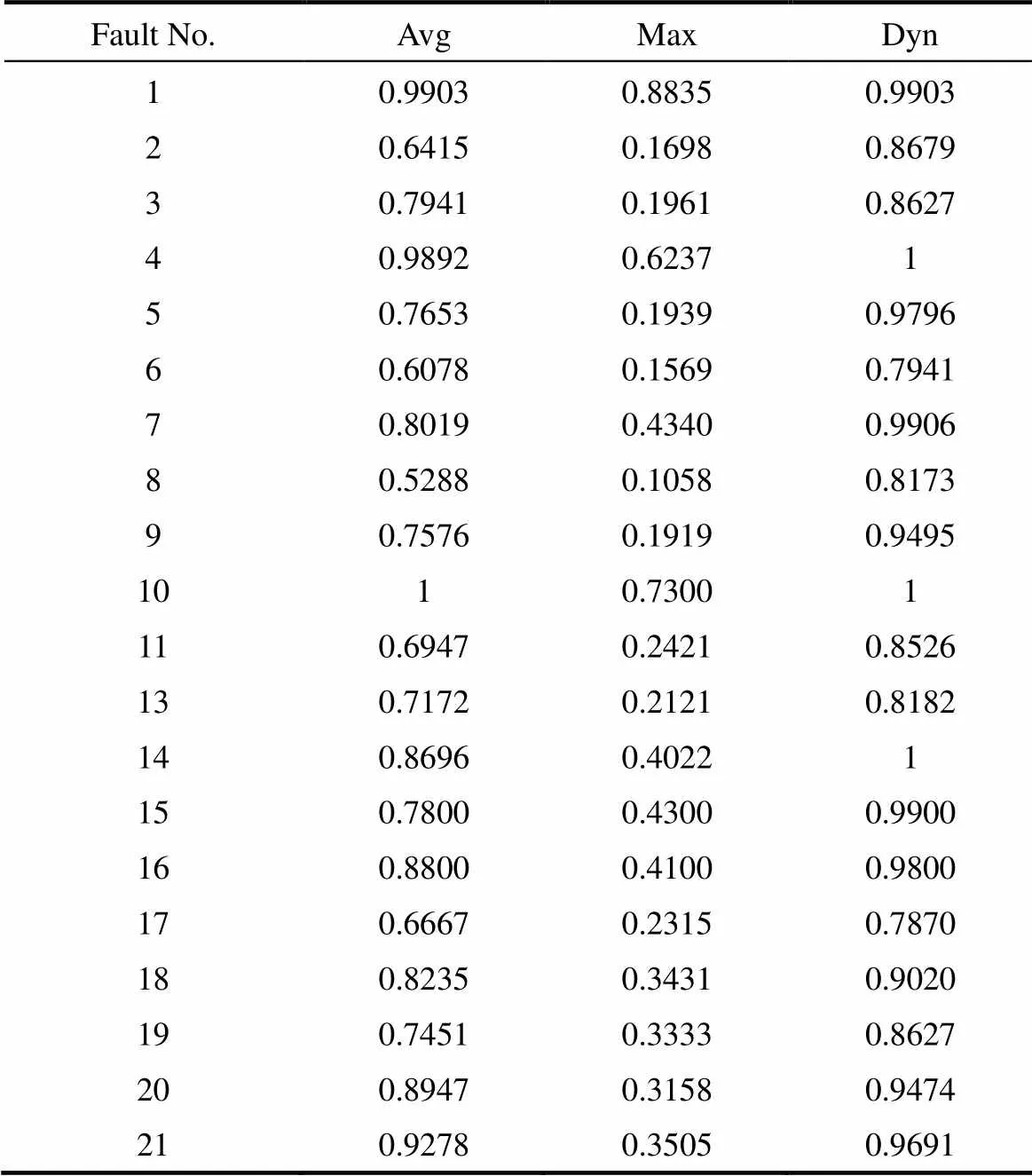
表4 金屬刻蝕過程故障批次檢測率

4 結 論

提出了一種基于核相似度SVDD的間歇過程監測方法。根據待監測過程數據的特性設定權重，靈活選擇不同支持向量對應的球心距作為該監測點的控制限，無需新增人為設定參數，對不同時段特性差異較大的過程數據具有較好的適應性，并且能夠很好地適應監測數據所具有的時變性，過程監測結果穩定。與現有基于SVDD的間歇過程監測方法相比，本文所提方法在不增加訓練樣本計算量的同時對正常過程數據的描述更準確，為間歇過程監測提供了更合理的控制限，有效地提高了過程監測的準確性。

References

[1] Jiang Q c, Yan X f. Just-in-time reorganized PCA integrated with SVDD for chemical process monitoring[J]. AIChE Journal, 2014, 60(3): 949-965.

[2] Hu Y, Ma H h, Shi H b. Enhanced batch process monitoring using just-in-time-learning based kernel partial least squares[J]. Chemometrics and Intelligent Laboratory Systems, 2013, 123(3): 15-27.

[3] Rashid M M, Yu J. Nonlinear and non-Gaussian dynamic batch process monitoring using a new multiway kernel independent component analysis and multidimensional mutual information based dissimilarity approach[J]. Industrial & Engineering Chemistry Research, 2012, 51(33): 10910-10920.

[4] Zhao C H, Sun Y X. Step-wise sequential phase partition (SSPP) algorithm based statistical modeling and online process monitoring[J]. Chemometrics and Intelligent Laboratory Systems, 2013, 125(5): 109-120.

[5] 趙春暉, 王福利, 姚遠, 等. 基于時段的間歇過程統計建模、在線監測及質量預報[J]. 自動化學報, 2010, 36(3): 366-374.Zhao C H, Wang F L, Yao Y,. Phase-based statistical modeling, online monitoring and quality prediction for batch processes[J]. Acta Automatica Sinica, 2010, 36(3): 366-374.

[6] 張建明, 葛志強, 謝磊, 等. 基于支持向量數據描述的非高斯過程故障重構與診斷[J]. 化工學報, 2009, 60(1): 168-171. ZHANG J M, GE Z Q, XIE L,. Non-Gaussian process monitoring and fault reconstruction and diagnosis based on SVDD[J]. CIESC Journal, 2009, 60(1): 169-171.

[7] 王培良, 葛志強, 宋執環. 基于迭代多模型ICA-SVDD的間歇過程故障在線監測[J]. 儀器儀表學報, 2009, 30(7): 1347-1352.Wang P L, Ge Z Q, Song Z H. Online fault monitoring for batch processes based on adaptive multi-model ICA-SVDD[J]. Chinese Journal of Scientific Instrument, 2009, 30(7): 1347-1352.

[8] MacGregor J F, Kourti T. Statistical process control of multivariate processes[J]. Control Engineering Practice, 1995, 3(3): 403-414.

[9] Kittiwachana S, Ferreira D L S, Lloyd G R,. One class classifiers for process monitoring illustrated by the application to online HPLC of a continuous process[J]. Journal of Chemometrics, 2010, 24(3/4): 96-110.

[10] Kittiwachana S, Ferreira D L S, Fido L A,. Self-organizing map quality control index[J]. Analytical Chemistry, 2010, 82(14): 5972-5982.

[11] Ning X H, Tsung F G. A density-based statistical process control scheme for high-dimensional and mixed-type observations[J]. IIE Transactions, 2012, 44(4): 301-311.

[12] NOMIKOS P, MACGREGOR J F. Monitoring batch processes using multiway principal component analysis[J]. AIChE Journal, 1994, 40(8): 1361-1375.

[13] NOMIKOS P, MACGREGOR J F. Multi-way partial least squares in monitoring batch processes[J]. Chemometrics & Intelligent Laboratory Systems, 1995, 30(1): 97-108.

[14] Chang K Y, Lee J M, Vanrolleghem P A,. On-line monitoring of batch processes using multiway independent component analysis[J]. Chemometrics and Intelligent Laboratory Systems, 2004, 71(2): 151-163.

[15] Lu N Y, Gao F R, Wang F L. Sub-PCA modeling and on-line monitoring strategy for batch processes[J]. AIChE Journal, 2004, 50(1): 255-259.

[16] Yao Y, Gao F R. A survey on multistage/multiphase statistical modeling methods for batch processes[J]. Annual Reviews in Control, 2009, 33(2): 172-183.

[17] Kang J H, Yu J, Kim S B. Adaptive nonparametric control chart for time-varying and multimodal processes[J]. Journal of Process Control, 2016, 37: 34-45.

[18] Gani W, Taleb H, Limam M. An assessment of the kernel-distance-based multivariate control chart through an industrial application[J]. Quality and Reliability Engineering International, 2011, 27(4): 391-401.

[19] Ge Z Q, Song Z H. Bagging support vector data description model for batch process monitoring[J]. Journal of Process Control, 2013, 23: 1090-1096.

[20] LEE J M, YOO C K, LEE I B. Fault detection of batch processes using multiway kernel principal component analysis[J]. Computers & Chemical Engineering, 2004, 28(9): 1837-1847.

[21] ZHANG Y W, HU Z Y. On-line batch process monitoring using hierarchical kernel partial least squares[J]. Chemical Engineering Research and Design, 2011, 89(10): 2078-2084

[22] Sun R X, Tsung F G. A kernel-distance-based multivariate control chart using support vector methods[J]. International Journal of Production Research, 2003, 41(13): 2975-2989.

[23] Camci F, Chinnam R B, Ellis R D. Robust kernel distance multivariate control chart using support vector principles[J]. International Journal of Production Research, 2008, 46(18): 5075-5095.

[24] Ning X H, Tsung F G. Improved design of kernel distance-based charts using support vector methods[J]. IIE Transactions, 2013, 45(4): 464-476.

[25] Sukchotrat T, Kim S B, Tsung F G. One-class classification-based control charts for multivariate process monitoring[J]. IIE transactions, 2009, 42(2): 107-120.

[26] Khediri I B, Weihs C, Limam M. Kernel k-means clustering based local support vector domain description fault detection of multimodal processes[J]. Expert Systems with Applications, 2012, 39(2): 2166-2171.

[27] Tax D M J, Duin R P W. Support vector domain description[J]. Pattern recognition letters, 1999, 20(11): 1191-1199.

[28] Tax D M J, Duin R P W. Support vector data description[J]. Machine Learning, 2004, 54(1): 45-66.

[29] Sakla W, Chan A, Ji J,. An SVDD-based algorithm for target detection in hyperspectral imagery[J]. Geoscience and Remote Sensing Letters, IEEE, 2011, 8(2): 384-388.

[30] Ge Z Q, Gao F R, Song Z H. Batch process monitoring based on support vector data description method[J]. Journal of Process Control, 2011, 21(6): 949-959.

[31] Yao M, Wang H G, Xu W L. Batch process monitoring based on functional data analysis and support vector data description[J]. Journal of Process Control, 2014, 24(7): 1085-1097.

Batch processmonitoring by kernel similarity-based support vector data description

WANG Jianlin, MA Linyu, LIU Weimin, QIU Kepeng, YU Tao

(College of Information Science and Technology, Beijing University of Chemical Technology, Beijing 100029, China)

Kernel distance-based support vector data description (SVDD) for batch process monitoring exhibited poor monitoring precision by setting control limit from the largest kernel distance in historical process dataset but ignoring hyperspherical irregularity in high dimensional space. A kernel similarity based SVDD monitoring method was proposed for batch process monitoring. Kernel similarity was taken as kernel function value between support vectors and data samples for testing. The weighted summation of kernel similarity and distance of support vectors at various time points was utilized to set dynamic control limit for data samples of batch process to be monitored. Batch process monitoring was achieved by judging if kernel distance of test sample exceeded the dynamic control limit. This monitoring method considered irregularity of hypersphere, local distribution characteristics of process dataset in high dimensional space, and spontaneity of data samples, so that it could improve accuracy in batch process monitoring. Method effectiveness was demonstrated by numerical simulation and metal etching process in semiconductor manufacturing.

kernel similarity; support vector data description; dynamic monitoring; batch process

10.11949/j.issn.0438-1157.20170428

TQ 277

A

0438—1157（2017）09—3494—07

2017-04-19收到初稿，2017-05-27收到修改稿。

王建林（1965—），男，教授。

國家自然科學基金項目（61240047）；北京市自然科學基金項目（4152041）。

2017-04-19.

Prof. WANG Jianlin, wangjl@ mail.buct.edu.cn

supported by the National Natural Science Foundationof China (61240047) and the Beijing Natural Science Foundation (4152041).