改進的精英教學優化算法及其在甲醇合成優化中的應用

王應，張凌波，顧幸生

?

改進的精英教學優化算法及其在甲醇合成優化中的應用

王應，張凌波，顧幸生

（華東理工大學化工過程先進控制與優化技術教育部重點實驗室，上海200237）

為了提高精英教學算法(ETLBO)的尋優能力，特別是精度差、尋優速度慢的問題，提出改進的精英教學算法。首先，通過自主學習過程，加強對優質解所在區域的局部勘探，提高算法的尋優效率。其次，引入“差異化幫扶”思想及自適應機制，對不同水平的學生施予適宜的、靈活的學習方式，有針對性的幫助，平衡了算法的勘探速度、精度。通過增加學生間的交流次數，提高了算法的全局勘探能力。標準函數優化結果表明，改進后的算法在尋優能力和勘探效率兩方面都有明顯提高。最后，建立甲醇合成的機理模型，將改進后的算法應用于甲醇合成過程的優化，取得了良好的效果。

算法；甲醇合成；精英教學算法；模型；優化

引 言

群體系統有著特定的規律性，由這些規律而啟發出的群智能系統模型，正在被廣泛地研究出來，如粒子群算法[1]、蟻群算法[2]、蜂群算法[3-6]等。教學算法是由Rao等[7]于2011年提出的一種源于對人類教學活動進行模擬的新型啟發式算法。“教學算法”(teaching-learning-based optimization, TLBO)分為兩個階段：教學階段，所有學生向老師學習，提高全體的成績；學習階段，學生間相互學習，提高個體成績。

教學算法(TLBO)具有快速收斂、參數少等[8]優點，但處理復雜問題效果欠佳，學者們分別對其進行了不斷的改進，如精英教學算法[9]、多目標優化[10-13]等，并廣泛應用于工業問題中，如甲醇合成轉化率軟測量[14]、機械設計/優化[15-17]、無人機路徑規劃[18]、電網動態重構/調度[19-20]、數據聚類/分類[21-25]、優化工藝/參數[26-27]等。

甲醇是重要的有機化工原材料，廣泛應用于有機合成、涂料和醫療應用等行業。甲醇合成過程的流程長、涉及變量多、非線性突出、各模塊耦合性強且實際工況復雜多變，難以確定最佳的控制參數。將參數調節與最新的群智能算法結合，獲得甲醇合成過程中優化參數，并實施，可以減少甲醇合成過程的損耗，降低企業的生產成本。

本文在精英教學算法(elitist TLBO, ETLBO)的基礎上，針對精英教學算法尋優精度低、速度慢的問題，提出改進的精英教學算法(modified ETLBO, mETLBO)。通過引入自主學習，提高其尋優速度；采用差異化“幫扶”策略，平衡算法的勘探精度和速度。標準測試函數的測試結果，表明改進后算法具有良好的尋優能力。最后，應用于Lurgi管殼式副產蒸氣甲醇合成過程的優化，并且在甲醇合成優化問題中取得了良好的效果。

1 精英教學算法

精英教學優化算法，分為教學階段、學習階段、精英策略3個階段。每個學生的成績為=(x,1,x,2, ,x,d)，是總科目數。班級人數為，初始化為=+(-)r,、分別為成績的上下限向量，r為0～1之間的隨機數。選取最優的學生為下一次迭代中的教師。具體步驟為如下。

（1）教學階段，全體學生向老師學習，其中班級、教學過程(次)分別為

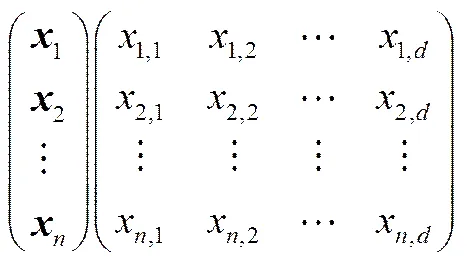
′=+r(X-×M) (2)

其中,X為最優個體(教師)的成績，=round(1+r) 為教學因子，M為班級平均成績；如果學習后的成績更好，則更新，否則不變。

（2）學習階段，對每個學生，如學生，隨機選一個學生向其學習，迭代過程為

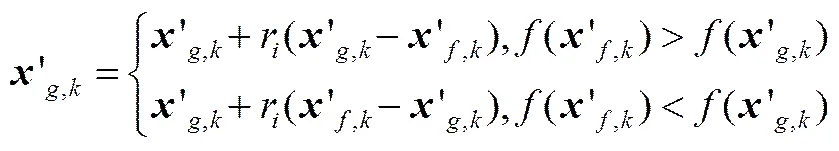
如果學習后的成績更好，則更新，否則不變。

（3）精英策略

淘汰成績差的學生，并用優秀的學生(精英解)替換。

2 改進的精英教學算法

由于ETLBO算法的尋優速度慢，精度差，亟需改進。在學習過程中，因為每個人的學習習慣、自我約束能力有差異，一部分學生能夠利用閑暇時間進行自主學習。即優秀的學生通過自主學習，強化了學習效果，成績提高得更快。在算法中引入此過程，由于較優解位于局部或全局最優的附近，通過加強對這些解所在區域的局部勘探，提高算法的尋優效率。

另外，對于成績差的學生，采用“幫扶”策略，彌補落下的知識，使其成績得以提高。差異化的“幫扶”策略可以針對不同水平的學生因材施教，給予學生差異化的學習指導，可以有針對性地幫助不同層次的學生彌補知識，提高其學習成績。即對不同層次的個體，施以不同的迭代步長，一方面，可以維持種群的多樣性，防止算法早熟；另一方面，可以防止算法陷入局部最優，增加了算法的穩定性。最后，增加學生之間的交流次數，分享知識，來提高學習者的成績。在ETLBO算法的基礎上，引入了上述的優化策略，具體如下。

2.1 自主學習

在學習過程中，優秀的學生在課后時間，自主學習各科知識，學習步長為

=(-) (4)

其中，為單位時間成績提高率，如圖1所示。根據冪律分布[28]，學習過程中，前期投入單位時間成績上升較快；反之，后期提高較慢。前期以較大的步長進行探索，提高算法的尋優速度，對于后期以較小的步長進行微細探索，而提高算法的精度。自主學習過程的偽代碼如下所示。

初始化參數，自主學習人數1，科目數

//各科學習（維度方向探索）

for1 to n

for1to

//e為科目的軸向單位向量(維)

if(x+e)<(x) then′=x+e；

if(x-e)<(x) then′=x-e；end if

end

end

//整體復習

if(+r·(′-))<(′) then″=+r·(′-)；end if

2.2 差異化“幫扶”策略

將班級學生按照成績進行排序，并劃分為A、B、C 3個等級。對低水平的學生，進行密切指導和督促，高強度的補差補缺；中等程度地進行適當的提醒和少量的查漏補缺；對于優秀的學生，給予自主學習的時間。根據學生的學習能力，有針對地精準化教學。算法運行中可以保留優秀學生的屬性，可以有效地防止算法陷入局部最優及種群的早熟。其公式為

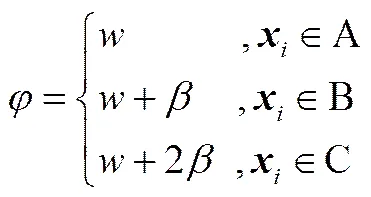
其中，為自適應步長，可以使算法可以靈活地適應最優值的波動，改善算法的全局尋優能力。

(6)

其中，1>2，；(·)為該次迭代的最優適應值；r為[0,1]間的隨機數。適應值變化快時，學習步長加大，適應值變化慢時，學習步長變小，動態跟隨并自適應調節，提高算法的靈活性。

將分級自適應因子代入式(2)，可得改進后的教學公式為

′=×[+r(X-×M)] (7)

2.3 交流反饋

學習交流只發生在部分人之間，按照概率(rand)，隨機選學生通過提高交流次數，提高學習者的成績。在兩點間采樣，遍歷采樣點，成績提高則替代。通過增加隨機的采樣點，提高對空間的感知能力，增加算法的全局勘探能力。

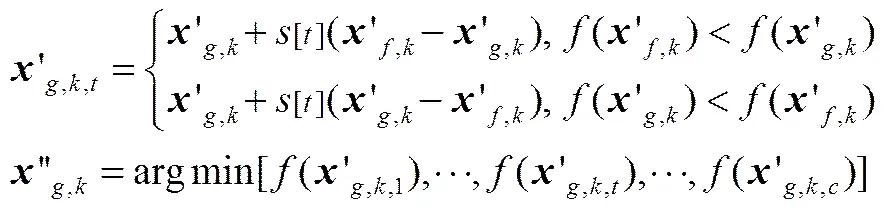
其中，=[r,r,…,r]為維隨機采樣矩陣。

（1）初始化班級，設置算法的參數；

（2）評價學生的適應度、記錄精英解、劃分等級；

（3）自主學習：選取優秀的學生，進行自主學習；

（4）教學階段：采用式(7)，對每個學生進行差異化教學；

（5）學習階段：采用式(8)，完成學生間的交流學習；

（6）精英解替換差解；

（7）滿足條件，則終止，否則轉步驟（2）。

為進一步規范縣人大代表述職工作，10月11日，縣人大常委會在城關街道組織召開縣人大代表述職評議現場觀摩會。縣人大常委會主任、分管副主任和各鎮人大主席、各街道人大工作室主任、各園（區）負責人大工作的同志參加了會議。觀摩會上，住城關街道的6名縣人大代表面對面向選區200多名選民代表作了述職報告。觀摩會后，縣人大常委會主任王晉成主持召開縣鎮人大代表述職評議工作動員部署會，要求各鎮（街、園、區）人大認真學習此次觀摩會，認真規范組織好代表述職活動，確保真述真評，不搞形式，不走過場，取得實效。

3 實驗與分析

3.1 實驗分析(一)

為了全面評價算法的性能，選取經典測試函數，如表1所示。為了評價算法處理不同復雜程度問題的能力進行20、30、50維測試，并與權威的算法ABC、I-ABC比較。為了客觀評價，取相同的共性參數，種群規模為40，最大40000次適應度評價，運行50次。特性參數，1、2、分別為0.75、0.25、0.35，自主學習人數1、科目數、精英人數都設為3，ABC、I-ABC數據取至文獻[29]。測試結果見表2，黑體表示算法尋得最優，精度為10-7。適應度曲線見圖2。

表1 無約束測試函數

表2 優化結果對比

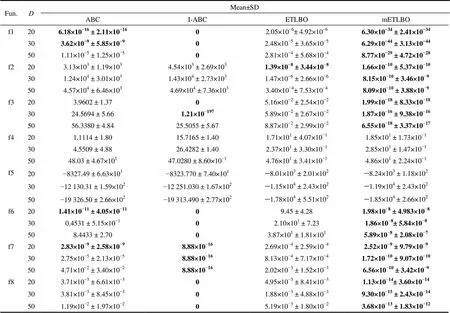
Table 2 Comparison of optimization results

（1）由表1可知，mETLBO算法在20、30、50維都尋得5次最優，且尋優精度非常高，優于其他算法。在50維復雜問題的處理上，改進后的算法也表現優異。此外，標準差的大小，反應算法的穩定性，其標準差也遠小于ETLBO等算法的標準差，說明算法具有良好的穩定性。

（2）由圖2可知，在單峰函數收斂上算法基本無差別，[圖2(a)、(d)]。但是在多模函數測試表現上，改進后的算法可以快速尋得最優，尤其是處理高維復雜的問題，尋優速度明顯好于其他算法[圖2(e)～(g)]。

（3）因Ackley、Schwefel 、Rastrigin函數存在很多局部最優點和局部凹區域，由圖2(c)、(e)、(f)、(g)可知，改進后的算法可以有效地跳出局部最優，而快速有效地尋得全局最優值，即mETLBO算法的全局搜索性能更好。

3.2 實驗分析(二)

為確定mETLBO算法的特性參數，先進行正交實驗，然后對結果進行顯著性分析和時間復雜度分析。考慮實驗(一)的結果，選擇較為復雜的測試函數f5～f10，可以更加準確及客觀地評價算法的性能。共性參數：為40，為30，為5，40000次適應度評價，精度10-7，獨立運行50次。

（1）算法參數的確定

選取多模測試函數(f5～f10)，分別進行正交實驗、方差分析，旨在確定各個策略的最佳的參數配置。正交表設計為L12(28)，改進的算法因子和水平參數見表3。分析結果見表4。

因方差分析中的顯著性指標(sig)越小，表明該參數的改變其對結果影響越顯著，故將參數影響按照權重大小次序排列，并由實驗結果確定最佳的參數。根據表4，可得最終參數確定為3、3、0.75、0.25、0.35、10、0.7、4。

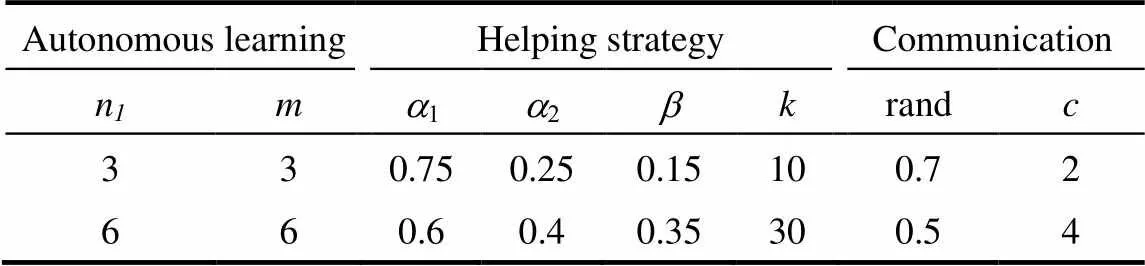
表3 正交因子、水平參數

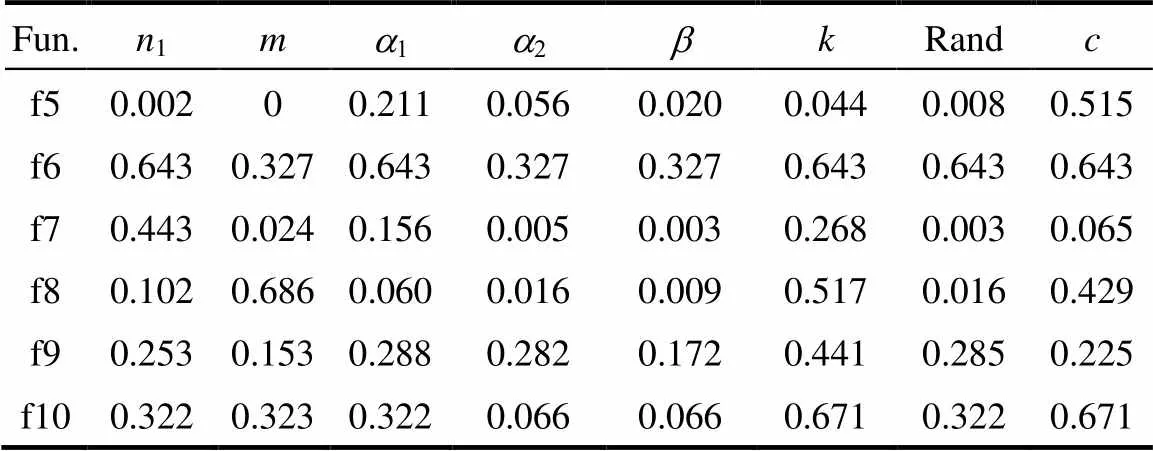
表4 正交實驗-方差分析(sig)

（2）顯著性檢驗及復雜度分析

根據正交實驗中確定的參數，進行測試，并對結果進行顯著性分析。即以ETLBO為對照組，進行Mann-Whitney顯著性檢驗。結果見表5。同時進行算法時間記錄，分析算法的運行效率，見表6。

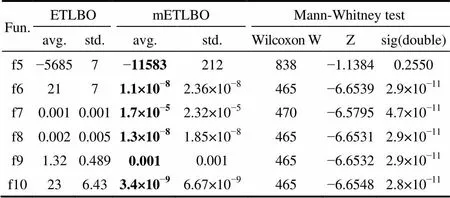
表5 實驗測試結果

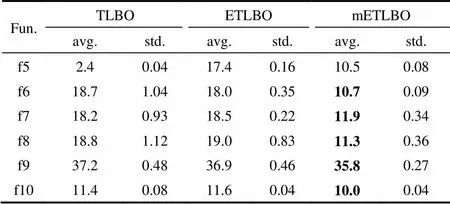
表6 運行時間統計

由表5可知，改進后的算法均明顯優于精英教學算法，且根據Mann-Whiteny顯著性檢驗，除f6不顯著外，其余均小于0.05，顯著性明顯，改進后的算法最優適應值下降的速度較快，能夠在相同適應度評價下，快速尋得最優值。

假設原算法有1個人向老師學習，共有個科目，則教師階段為1次學習，學習階段為21次學習，精英替代為2次，次循環的復雜度為[(1212)]；改進后的算法則為[(1rand×2123)]，3為自主學習次數；因為rand為交流概率，小于1，因此(ETLBO)>(mETLBO)，改進后的算法時間復雜度較小，提高了算法的效率。mETLBO算法的時間復雜度更低，如表6所示，mETLBO算法運行時間均小于ETLBO。

（3）不同策略的對比

為分析3種策略的有效性及相互關系，分別將其單獨加入到ETLBO算法上,測試函數(f5～f10)，特性參數為正交實驗的結果，維數為30。不同策略的迭代曲線如圖3所示。

如圖3(a)、(b)、(c)、(e)、(f)所示，mETLBO算法的尋優能力，總能夠與最有效的策略保持一致性。說明策略間的相互影響較小，且通過混合所有策略可以使算法適用面更加廣泛，提高了算法解決不同問題的能力。

4 甲醇合成優化應用

4.1 甲醇合成工藝及模型驗證

甲醇是主要的化工有機的原材料，對其合成過程進行建模與優化至關重要。常見的甲醇合成工藝是Lurgi工藝，屬于低壓、銅基、等溫反應工藝。其生產過程包括3個基本步驟：① 合成氣的制備；② 合成氣轉化為甲醇；③ 甲醇的分離和純化。針對Lurgi管殼式副產蒸氣甲醇合成過程，采用文獻[30]所述的C301銅基催化劑甲醇合成本征動力學方程，選擇CO、CO2加氫為關鍵反應，CO、CO2為關鍵組分，建立甲醇合成過程的機理模型。其中，CO、CO2濃度隨著床層高的變化為

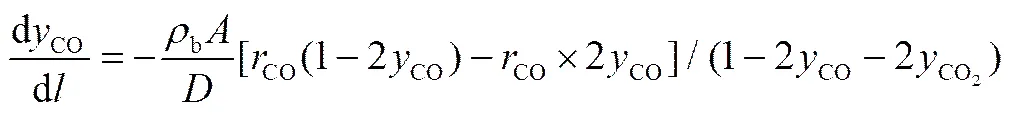
(10)

根據熱量衡算，可得反應床溫度隨著床高的變化，為

其中，CO、CO2分別為單位質量催化劑上的反應速率；b為床層堆積密度，為催化床橫截面積。b、f分別為床層與管外介質溫度，cb為混合物的摩爾熱容；-DRCO、-DRCO2分別為CO、CO2加氫反應的熱效應，T為催化床中混合氣體的摩爾流量，bf、i、a分別為床層與冷卻介質間的傳熱系數，反應管根數及反應管平均直徑。

某Lurgi管殼式副產蒸氣甲醇合成器，管長5800 mm，反應管尺寸44 mm×2 mm，共4309根。根據文獻[31]的某廠2016年的實際生產數據的模型估計參數，建立實際工業模型。從生產報表中摘錄5組數據進行模型驗證，得到結果見表7。in是入塔溫度，w是沸騰水溫度。由結果可知催化床溫度的分布，出塔的CO和CO2摩爾分數(CO、CO2)很好地貼合實際工業數據。

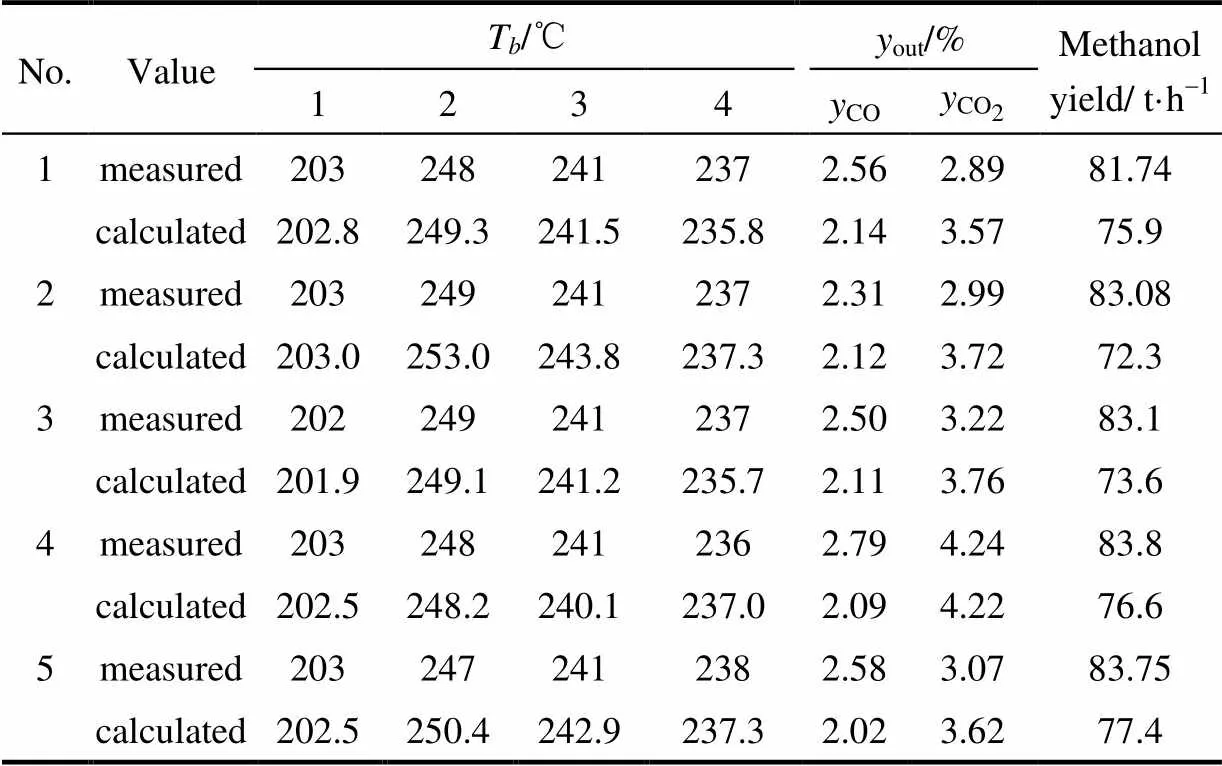
表7 模擬計算結果與工廠生產數據比較

4.2 甲醇合成的優化

甲醇合成中的各項生產控制因素，如反應壓力、溫度、循環氣量等參數都影響甲醇合成回路中的能源消耗和物料消耗。在實際生產中，循環氣量調節不恰當會使功耗增加，馳放氣調節不當會增加物料消耗，即：（1）當加大循環氣流量時，馳放氣減小，但壓縮機功耗也會增加，物料消耗減少，能源消耗增加；反之，減小循環氣流量，壓縮機功耗會減小，但馳放氣的排放會增加，導致有效氣體因排除而浪費。循環氣流量與馳放氣流量的關系[圖4(a)]；（2）隨著循環氣流量的不斷增加，甲醇產量增加較快，但是循環氣流量到一定值時，甲醇的產量則維持在某一穩定值[圖4(b)]。此時，如果繼續增加循環氣流量，則會增加無效的壓縮機功耗，增加了能源消耗，所以存在著物料消耗和能源消耗的優化問題。模型的新鮮氣體積流量設為4×104m3·h-1，成分（體積分數）如表8所示。

表8 新鮮氣成分

確定相應的優化目標，在一定新鮮氣組分、流量、合成壓力、管間水溫度等條件下確定合適的循環氣流量，使甲醇合成塔的生產單位甲醇所產生的功耗和物料消耗最低，即生產每單位甲醇所耗費的費用最低，為

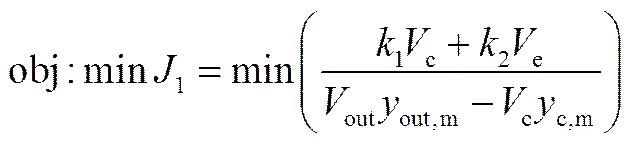
s.t.

（1）軸向濃度約束：式（9），式（10）

（2）軸向溫度約束：式（11）

（3）循環氣體積約束：3×105m3·h-1

（4）床層溫度：240℃

（5）合成氣溫度：225℃<<255℃

（6）沸騰鍋爐水壓力：4.0～5.5 MPa

其中，1為1 m3循環氣的壓力經壓縮機加壓到入塔壓力產生的能耗費用，1=38.4 kJ·m-3；2為1 m3馳放氣的排放產生的物耗費用，2=4084.5 kJ·m-3；c為循環氣的氣體體積；e為馳放氣的氣體體積；out為出塔氣的氣體體積；out,m為出塔氣中甲醇氣體的百分比；c,m為循環氣中甲醇氣體的百分比。

將目標函數帶入算法中，參數與正交實驗所確定的參數相同，進行優化，尋優結果見表9。

表9 甲醇合成優化結果

由圖5可知，改進后的算法可以有效優化甲醇合成中的循環氣流量和H/C等參數，且適應度下降較快，尋得的甲醇單耗更低。由表9可知，在給定新鮮氣流量及成分情況下，以甲醇單耗最低為目標時，合成塔壓力為4.2 MPa，循環氣流量應控制為4.7927×105m3·h-1，此時甲醇產量為380.3 kmol·h-1；合成塔壓力為4.3 MPa，循環氣流量應控制為5.1586×105m3·h-1，此時甲醇產量為385.8 kmol·h-1。

5 結 論

本文提出了一種改進的精英教學算法，主要進行了3個方面的改進：

（1）引入自主學習過程，加強了優質解對其所在區域的局部勘探；

（2）引入差異化幫扶策略；

（3）設計了步長自適應及差異化自適應策略，平衡算法的綜合性能，并分析不同參數對算法性能的影響。測試函數結果揭示出自主學習、差異化幫扶、自適應策略可以有效提高算法性能。最后，應用于甲醇合成過程的優化，能夠有效降低甲醇合成回路的能源和物料消耗，提高了經濟效益。

References

[1] KENNEDY J, EBERHART R. Particle swarm optimization[C]// Proceedings of IEEE International Conference on Neural Networks. 1995, 4: 1942-1948.

[2] MANIEZZO D M, COLORNI V A. The ant system: optimization by a colony of cooperating agents[J].IEEE Trans. on Systems, Man, and Cybernetics B, 1996, 26(1): 29-41.

[3] AKAY B, KARABOGA D. A modified artificial bee colony algorithm for real-parameter optimization[J]. Information Sciences, 2012, 192(1): 120-142.

[4] BANHARNSAKUN A, ACHALAKUL T, SIRINAOVAKUL B. The best-so-far selection in artificial bee colony algorithm[J]. Applied Soft Computing, 2011, 11(2): 2888-2901.

[5] WU B, QIAN C H. Differential artificial bee colony algorithm for global numerical optimization[J]. Journal of Computers, 2011, 6(5): 841-848.

[6] CHEN S M, SAROSH A, DONG Y F. Simulated annealing based artificial bee colony algorithm for global numerical optimization[J]. Applied Mathematics & Computation, 2012, 219(8): 3575-3589.

[7] RAO R V, SAVSANI V J, VAKHARIA D P. Teaching-learning-based optimization: a novel method for constrained mechanical design optimization problems[J]. Computer-Aided Design, 2011, 43(3): 303-315.

[8] SATAPATHY S C, NAIK A. Modified teaching-learning-based optimization algorithm for global numerical optimization—a comparative study[J]. Swarm & Evolutionary Computation, 2014, 16: 28-37.

[9] RAO R V, PATEL V. An elitist teaching-learning-based optimization algorithm for solving complex constrained optimization problems[J].Int. J. Ind. Eng. Comput., 2012, 3(4): 535-560.

[10] PATEL V, SAVSANI V. Multi-objective optimization of a stirling heat engine using TS-TLBO (tutorial training and self learning inspired teaching-learning based optimization) algorithm[J]. Energy, 2016, 95: 528-541.

[11] RAJA B D, JHALA R L, PATEL V. Multi-objective optimization of a rotary regenerator using tutorial training and self-learning inspired teaching-learning based optimization algorithm (TS-TLBO)[J]. Applied Thermal Engineering, 2016, 93: 456-467.

[12] PATEL V K, SAVSANI V J. A multi-objective improved teaching-learning based optimization algorithm (MO-ITLBO)[J]. Information Sciences, 2016, 357: 182-200.

[13] SIVADURGAPRASAD C, KOMMADATH R, KOTECHA P. A note on multi-objective improved teaching-learning based optimization algorithm (MO-ITLBO)[J]. Information Sciences, 2016, 373: 337-350.

[14] 雙翼帆, 張凌波, 顧幸生.基于高斯過程和改進教與學優化算法的甲醇合成轉化率軟測量[J]. 華東理工大學學報(自然科學版), 2016, (3): 369-374. SHUANG Y F, ZHANG L B, GU X S. Soft sensor of conversion rate in methanol synthesis based on Gaussian process and improved teaching-learning-based optimization[J]. Journal of East China University of Science and Technology(Nature Science), 2016, (3): 369-374.

[15] TO?AN V. Design of planar steel frames using teaching-learning based optimization[J]. Engineering Structures, 2012, 34: 225-232.

[16] CAMP C V, FARSHCHIN M. Design of space trusses using modified teaching-learning based optimization[J]. Engineering Structures, 2014, 62: 87-97.

[17] DEDE T, AYVAZ Y. Combined size and shape optimization of structures with a new meta-heuristic algorithm[J]. Applied Soft Computing, 2015, 28: 250-258.

[18] 武巍, 鄒杰. 基于改進教-學算法的無人機航路規劃[J].計算機應用, 2016, 36(9): 2626-2641. WU W, ZOU J.Route planning method for unmanned aerial vehicle based on improved teaching-learning algorithm[J]. Journal of Computer Applications, 2016, 36(9): 2626-2641.

[19] 時慧喆, 劉志鵬, 鐘文強. 基于混合優化算法的配電網動態重構研究[J].電氣技術, 2016, 17(6): 41-46. SHI H Z, LIU Z P, ZHONG W Q. The research for dynamic distribution network reconfiguration based on hybrid optimization algorithm[J]. Electrical Engineering, 2016, 17(6): 41-46.

[20] MANDAL B, ROY P K. Optimal reactive power dispatch using quasi-oppositional teaching learning based optimization[J]. International Journal of Electrical Power & Energy Systems, 2013, 53: 123-134.

[21] SATAPATHY S C, NAIK A. Data Clustering based on teaching-learning-based optimization[C]// International Conference, Semcco, Visakhapatnam, Andhra Pradesh, India, December. DBLP, 2011: 148-156.

[22] SAHOO A J, KUMAR Y. Modified Teacher Learning Based Optimization Method for Data Clustering[M]//Advances in Signal Processing and Intelligent Recognition Systems. Springer International Publishing, 2014: 429-437.

[23] NAIK B, NAYAK J, BEHERA H S,. A self adaptive harmony search based functional link higher order ANN for non-linear data classification[J]. Neurocomputing, 2016, 179: 69-87.

[24] PANIGRAHI S K, PATTNAIK S. Empirical study on clustering based on modified teaching learning based optimization[J]. Procedia Computer Science, 2016, 92: 442-449.

[25] MURTY M R, NAIK A, MURTHY J V R,. Automatic clustering using teaching learning based optimization[J]. Applied Mathematics, 2014, (5): 1202-1211

[26] VENKATA RAO R, KALYANKAR V D. Parameter optimization of machining processes using a new optimization algorithm[J]. Materials and Manufacturing Processes, 2012, 27(9): 978-985.

[27] RAO R V, KALYANKAR V D. Parameter optimization of modern machining processes using teaching-learning-based optimization algorithm[J]. Engineering Applications of Artificial Intelligence, 2013, 26(1): 524-531.

[28] ANDRIANI P, MCKELVEY B. From Gaussian to Paretian thinking: causes and implications of power laws in organizations[J]. Organization Science, 2009, 20(6): 1053-1071.

[29] LI G, NIU P, XIAO X. Development and investigation of efficient Artificial Bee Colony algorithm for numerical function optimization[J]. Appl.Soft Comput., 2012, 12(1): 320-332.

[30] 謝克昌, 房鼎業.甲醇工藝學[M]. 北京: 化學工業出版社, 2010: 175-195. XIE K C, FANG D Y. Methanol Technology[M]. Beijing: Chemical Industry Press, 2010: 175-195

[31] 俞靈杰, 張凌波, 顧幸生. 基于改進狼群算法的甲醇合成塔轉化率機理建模及參數估計[J]. 華東理工大學學報(自然科學版), 2017, (5), 待發表. YU L J, ZHANG L B, GU X S. Mechanism modeling and parameter estimation of conversion rate in methanol synthesis tower based on improved wolf pack algorithm[J]. Journal of East China University of Science and Technology(Nature Science), 2017, (5), in press.

Application of modified elitist teaching-learning-based optimization algorithm to process optimization of methanol synthesis

WANG Ying, ZHANG Lingbo, GU Xingsheng

(Key Laboratory of Advanced Control and Optimization for Chemical Processes, Ministry of Education, East China University of Science and Technology, Shanghai 200237, China)

Elitist teaching-learning-based optimization (ETLBO) algorithm is inspired by practical teaching-learning process. A novel group search optimizer, modified elitist teaching-learning-based optimization (mETLBO), was proposed to improve low precision and poor stability of the ETLBO. First, an autonomous learning process was introduced to strengthen local search of high quality solution so as to improve algorithm’s elite-searching speed. Second, differentiated support and self-adaptive strategy providing appropriate and flexible learning approach to students at various levels, were applied to offer desirable assistance and balance searching rate and accuracy of the algorithm. Third, global searching ability of the algorithm was enhanced by increasing communication frequency between students. Optimization results on standardized functions show that the proposed algorithm is obviously superior to the original one in performance and efficiency. Finally, satisfactory results were achieved by applying the improved algorithm to process optimization with mechanism model of methanol synthesis.

algorithm; methanol synthesis; ETLBO; model; optimization

10.11949/j.issn.0438-1157.20170146

TP 273

A

0438—1157（2017）08—3141—11

張凌波。第一作者：王應（1993—），男，碩士研究生。

國家自然科學基金項目（61573144）。

2017-02-16收到初稿，2017-04-19收到修改稿。

2017-02-16.

ZHANG Lingbo, zlb@ecust.edu.cn

supported by the National Natural Science Foundation of China (61573144).