羅布麻纖維混紡織物綜合性能分析與混紡比優選設計

顧秦榕 謝春萍 吉宜軍 蘇旭中 劉新金

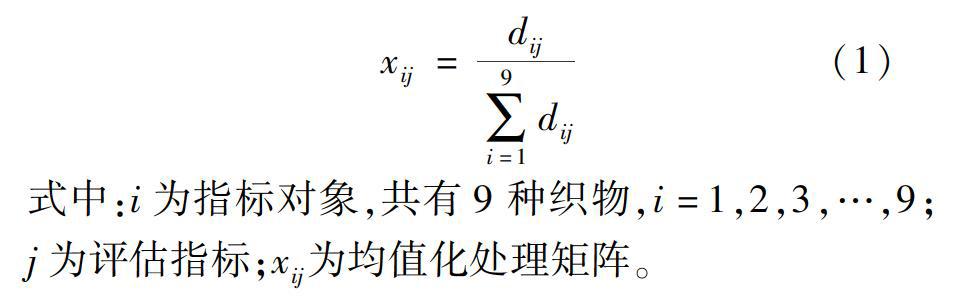
摘要： 羅布麻纖維是一種天然纖維，其功能保健性混紡產品的開發正愈來愈受到人們的歡迎。文章采用灰色聚類分析法對羅布麻/腈綸/莫代爾混紡針織物與亞麻/棉混紡針織物的綜合性能進行研究，優選出羅布麻/腈綸/莫代爾混紡針織物性能良好。采用線性加權和法建立一種多目標化函數的優化模型，求解出用于不同生產用途的織物的最佳混紡比。結果表明：羅布麻/腈綸/莫代爾織物的綜合性能優于亞麻/棉混紡織物與純棉織物；當羅布麻纖維理論含量為20%、29%及50%時分別可以達到織物加工性能優良、外觀效應佳、保健性好的設計效果。

關鍵詞： 灰色聚類分析；線性加權和法；羅布麻；混紡比；優化

中圖分類號： TS102.229

文獻標志碼： A

文章編號： 1001-7003（2017）12-0054-05

Abstract： Apocynum fiber is a natural fiber. The development of functional blended products is becoming more and more popular. In this paper， grey clustering analysis was used to study combination properties of apocynum/ acrylic fibers/ modal blended fabrics and linen/cotton blended fabrics， and the performance of apocynum/ acrylic fibers/ modal blended fabrics was good. The linear weight sum method was applied to establish an optimization model of multi-target function so as to solve the optimal blending ratio of different fabrics. The results show that， the comprehensive performance of the apocynum/ acrylic fibers/ modal blended fabrics is better than that of linen /cotton blended fabric. The design effect of good processing property， appearance and health keeping can be achieved when theoretical content of apocynum fiber is 20%，29% and 50%， respectively.

Key words： grey clustering analysis； linear weight sum method； apocynum； blending ratio； optimization

目前，在研究具有多個要素的對象時，傳統的科學研究思維方式正逐步向系統論方法過渡[1]。系統論方法主要以把握整體性、綜合性、相關性、動態性為基本原則，它是一種在多個要素彼此制約、相互聯系的關系中，系統地分析研究對象的方法。

本文將灰色聚類分析[2]與線性加權和法[3]這兩種思想引入到織物混紡比設計中，灰色聚類分析是指在信息不完全與非唯一的情況下，通過對少量的已知信息延伸并研究，進而上升到對系統的探究，尋找優化方法獲得最佳效果的算法。線性加權和法是按照加工目標的重要性分別賦予其對應的權系數，通過線性組合求最優的一種多目標規劃問題的方法。以羅布麻、亞麻混紡織物為例，采用灰色聚類分析法綜合評定兩類織物的優劣性，先對比優選出較優的織物。然后將麻纖維含量視為決策變量，將麻類混紡織物的各項基本性能視為目標函數，采用Matlab軟件Cftool工具箱對實驗數據進行擬合，得到目標函數。分別從織物的不同用途賦予目標函數不同的加權系數，將多目標函數轉化成單目標函數，對函數進行求解，得到不同用途時織物的最佳混紡比。通過灰色聚類分析及Matlab優化模型的建立，從新的角度對紡織產品混紡比進行優化設計，為混紡織物的設計與開發提供理論性的依據。

1 織物的優選

1.1 儀器與材料

儀器：YG301破裂試驗機、YG（B）522型耐磨試驗機（南通宏大實驗儀器有限公司），HH-4型數顯恒溫水浴鍋芯吸效應測試儀（江蘇盛藍儀器制造限公司），YG（B）416E型數字式測試儀測量織物的透氣性（寧波紡織儀器廠），PhabrOmeter織物手感評價系統（美國欣賽寶科技有限公司）。

織物：織物組織采用平針，平方米質量146g/m2，厚度0.37mm，橫密62線圈數/5cm，縱密49線圈數/5cm。

1.2 實 驗

由于織物的性能較多，且每種性能代表不同的含義，彼此之間聯系較少，很難簡單地評價織物性能的好壞，因此采用灰色聚類分析法來綜合評價織物的性能。本文分別采用YG 301破裂試驗機測量織物的頂破性，YG（B） 522型耐磨試驗機測量織物的耐磨性，HH-4型數顯恒溫水浴鍋芯吸效應測試儀測量織物的毛細芯吸性能，YG（B） 416E型數字式測試儀測量織物的透氣性，PhabrOmeter織物手感評價系統測試織物的風格效應，按照紡織品抗菌性能測試標準GB/T209944.3—2008《紡織品 抗菌性能的評價 第3部分：振蕩法》測試織物對大腸桿菌的抑菌效應。每塊試樣測試10組數據取平均值，測試數據如表1所示，其離散系數在5%～15%范圍內。

1.3 矩陣的構建

本文選取9種織物的頂破性、耐磨性、芯吸效應、透氣性、硬挺度、柔軟度、光滑度、懸垂性、手感值、抗菌性這10個評價因子構造矩陣dij。由于耐磨性的評價指標是失重率，失重率越大耐磨性越差，可以看出耐磨性與聚類指標呈負相關，為了使所有的評價因子與聚類指標關系保持統一性，將耐磨性數值以100減去失重率記錄，得到織物剩余重量百分率，使得織物耐磨性與聚類指標呈正相關。其次測試的數據彼此之間沒有聯系，因此需要將它進行均值化處理從而變成無量綱數值[4]。利用Matlab軟件將矩陣dij根據公式（1）均值化處理后得到一個9×10的均值化處理矩陣，如式（2）所示。

1.3 聚類系數的確定

聚類系數表示一個圖形中節點聚集程度的系數，聚類系數越大，相當于在這個灰度區間內出現的概率越大。將各因子的評價等級分為高類、中類、低類三種灰度等級[5]，記為K1、K2、K3，即灰度s為3。根據邊界值λjk與白化權函數fkj（x）確定指標j在聚類中的聚類系數[5]，從而確定織物的綜合性能，灰色聚類系數矩陣σki如式（3）所示。

根據綜合聚類系數，即公式（3），在同一灰度下比較各織物的優劣等級，可以看出羅布麻48/腈綸20/莫代爾32與羅布麻40/腈綸33/莫代爾27織物的高類灰度區間的聚類系數分別是0.9060與0.8046，相比于其他混紡織物優勢明顯。9種織物的綜合性能的排名依次是：羅布麻48/腈綸20/莫代爾32>羅布麻40/腈綸33/莫代爾27>羅布麻34/腈綸43/莫代爾23>羅布麻30/腈綸50/莫代爾20>亞麻43/棉57>純亞麻>棉>亞麻30/棉70>羅布麻30/棉70。當羅布麻含量達到40%及以上時，織物的綜合性能最佳；且羅布麻/腈綸/莫代爾的綜合性能比亞麻混紡織物與棉織物好。由此可以進一步研究根據不同的生產用途，設計羅布麻/腈綸/莫代爾混紡織物的理論最優混紡比。

2 優化模型的建立

2.1 目標函數

本文研究的目標織物為羅布麻/腈綸/莫代爾混紡織物。研究對象是織物的綜合性能，而不是單一的性能，把每個性能看成一個目標，研究多目標的最優問題。因此需要建立一個多目標函數，設有n個目標，目標函數分別為F1（x）、F2（x）、F2（x）……Fn（x）[6]。多目標函數的優化設計就是求解max{F1（x）、F2（x）、F3（x）……Fn（x）}。其中，X表示決策變量，Fn（x）表示目標函數。本次實驗設計決策變量X就是羅布麻纖維含量，目標函數Fn（x）就是羅布麻/腈綸/莫代爾混紡織物的綜合性能。

本文以影響生產加工的耐磨性，與外觀息息相關的懸垂性及決定織物保健性能的抗菌性三者為研究目標，建立多目標優化函數。織物的耐磨性越好，經過摩擦前后的質量損失率應當越小，加工過程中越不易斷頭；織物懸垂性越好其外觀效應更好；織物抑菌率愈大，保健性能便愈佳。

將織物耐磨性能看做目標函數F1（x），懸垂性看做目標函數F2（x），抗菌性看做目標函數F3（x）。構成多目標優化函數max{F1（x）、F2（x）、F3（x）}。將實驗數據歸一化處理，采用Matlab軟件Cftool工具箱進行多項式擬合，得到的函數關系表達式如表2所示。表2中置信區間表示的是某個參數的實際值在函數曲線結果范圍內的程度，它是一種概率，置信區間值越大，表示函數表達式的可信程度越高[7]。

2.2 加權系數

所謂加權，即是為強調某一要素在整個要素體系中的重要程度而賦予的某一特征值，特征值一般用數值表示，稱為這一要素的加權系數[8]。紡織品的設計過程中，根據紡織品的不同用途，其所需的特性也會有所不同。對于內衣型織物，由于其經常與手肘、膝蓋摩擦，要求其耐磨性凸出；對于外穿織物，為了追求完美的視覺效果，要求其懸垂性能較好；對于襪子等容易滋生細菌的織物，要求其具備一定的抗菌保健性能。在基于多目標化的紡織品設計中，可以根據纖維間特性的不同，通過調節混紡比來達到紡織品的不同加工需求。

在本實驗中，采用層次分析法確定每一類需求的紡織品各性能指標占所有性能指標的權重[9]，用wn表示，n=1、2、3，滿足0≤wn≤1，且∑3n=1ωn=1。y1表示耐磨性占織物性能的比重，y2表示懸垂性占織物性能的比重，y3表示保健性能占織物性能的比重。根據生產設計經驗，加權系數設計值如表3所示。

2.3 混紡比優化計算

線性加權和法，又稱“加法”合成法或加權算術平均算子，它是采用線性模型進行綜合評價的[10]。利用線性加權和法，通過公式（4），求解各項評價指標值與其對應的權系數的積之和的最大值，其對應的羅布麻纖維含量即是理論最優含量，利用Matlab軟件對多目標化函數進行求解。

Y=∑3i=1Fi（x）ωi（4）

式中：Y為織物的綜合評價值，Fi（x）為織物的評價指標，wi為織物各項指標的權重系數。

求解得到三種不同設計方案的羅布麻纖維含量依次是20%、29%、50%。因此，當織物要求加工性能優良的時候，其羅布麻理論最優含量應為20%；要求織物外觀風格效應好的時候，羅布麻理論最優含量應為29%；要求保健性優良的時候，羅布麻理論最優含量應為50%。本文不討論莫代爾纖維與腈綸纖維的含量，而將兩者視為一個整體，主要考慮羅布麻纖維的含量對織物綜合性能的影響。由于實驗局限性的存在，目前無法生產出羅布麻纖維含量分別為20%、29%、50%的紗線與織物，所以目前尚不能對理論設計結果進行驗證，這將是下一步的研究目標與重點。

運用Matlab軟件進行多目標函數模型的建立可以尋找出不同用途時羅布麻纖維的理論最優含量，此最優混紡比可能目前在實際生產過程中開發較困難，但是推進了羅布麻混紡織物的生產研究。同時由于羅布麻纖維長度短，難以成網；其次羅布麻纖維價格昂貴，因此控制羅布麻纖維含量有利于在織物綜合性能較好的基礎上控制好生產成本，企業在實際應用中可以進行更有針對性的設計生產，提高生產效率，為羅布麻混紡織物的設計與開發提供新的理論性依據。

3 結 論

1）采用灰色聚類分析法發現，羅布麻/腈綸/莫代爾混紡織物的綜合性能優于亞麻/棉混紡織物與純棉織物。

2）基于多目標函數求最優采用線性加權和法是直接從織物的綜合性能出發，優選最優的混紡比織物，概念最為清晰，得出的評估結論非常直觀。當織物分別要求加工性能優良、外觀風格效應良好、保健性優良時，羅布麻纖維理論最優含量分別為20%、29%、50%，為羅布麻混紡織物的生產與開發提供了很好的借鑒作用。

參考文獻：

[1]常紹舜.從經典系統論到現代系統論[J].系統科學學報，2011，19（3）：1-4.

CHANG Shaoshun. From classical system in the case of modern system theory[J]. Chinese Journal of Systems Science，2011，19（3）：1-4.

[2]王永剛，胡開元.一種基于改進灰色聚類分析的綜合評價方法[J].中國民航大學學報，2010，28（1）：48-51.

WANG Yonggang， HU Kaiyuan. Comprehensive evaluation method based on improved gray-clustering analysis[J]. Journal of Civil Aviation University of China，2010，28（1）：48-51.

[3]張羅漫，陳飛，胡琳.綜合評價中各指標加權系數確定方法的探討[J].中國衛生統計，1992，9（3）：21-25.

ZHANG Luoman， CHEN Fei， HU Lin. An approach to determing the weighted coefficient of indexes in comprehensive evaluation[J]. Chinese Journal of Health Statistics，1992，9（3）：21-25.

[4]鄧聚龍.灰色系統理論教程[M].武漢：華中理工大學出版社，1992：112-114.

DENG Julong. Microbiology[M]. Wuhan： Huazhong University of Science & Technology Press，1992：112-114.

[5]劉思峰，謝乃明.基于改進三角白化權函數的灰評估方法[C]//第16屆全國灰色系統學術會議論文集，2008：118-129.

LIU Sifeng， XIE Naiming. A new grey evaluation method based on reformative triangular whitenization weight function[C]//Proceedings of the 16th National Conference on Grey Systems，2008：118-129.

[6]LEUNGA S Y S， WONGA W K， MOK P Y. Multiple-objective genetic optimization of the spatial design for packing and distribution cartoon boxes[J]. Computers & Industrial Engineering，2008，54（4）：889-902.

[7]蔣增強，劉明周，趙韓，等.基于多目標優化的產品協同開發任務調度研究[J].農業機械學報，2008，39（3）：154-158，162.

JIANG Zengqiang， LIU Mingzhou， ZHAO Han， et al. Task scheduling of product cooperative development based on multi-objective optimization[J]. Transactions of the Chinese Society for Agricultural Machinery，2008，39（3）：154-158，162.

[8]李輝芹，鞏繼賢，黃故.基于MatLab優化工具的混紡織物混紡比設計[J].紡織學報，2009，30（10）：62-65.

LI Huiqin， GONG Jixian， HUANG Gu. Design of blending ratio based on Matlab toolbox[J]. Journal of Textile Research，2009，30（10）：62-65.

[9]李輝芹，鞏繼賢，黃故.基于多目標優化的混紡織物設計研究[J].棉紡織技術，2009，37（6）：20-23.

LI Huiqin， GONG Jixian， HUANG Gu. Research of blended fabric based on multiple objective optimization[J]. Cotton Textile Techology，2009，37（6）：20-23.

[10]孫瑋瑋，李雷.基于線性加權和法的大壩風險后果綜合評價模型[J].中國農村水利水電，2011（7）：88-90.

SUN Weiwei， LI Lei. The comprehensive hazard assessment model for the consequences caused by the dam failure based on the linear weighted method[J]. China Rural Water and Hydropower，2011（7）：88-90.