基于終端滑模面的導彈滑模控制器設計

華思雨,王旭剛

(南京理工大學 能源與動力工程學院,江蘇 南京 210094)

基于終端滑模面的導彈滑模控制器設計

華思雨,王旭剛

(南京理工大學 能源與動力工程學院,江蘇 南京 210094)

為了研究滾轉導彈的非線性控制特性,基于導彈簡化的非線性動力學模型,采用基于趨近律的滑模控制器設計方法,設計了含有過載跟蹤誤差及其積分的自適應終端滑模面,使系統的狀態在一開始到達并維持在滑模面上;采用雙曲正切切換函數代替符號切換,以消除系統存在的抖振;根據滑模運動的漸進穩定性及其動態品質,設計滿足要求的滑模變結構控制律;進行了控制算法的Simulink仿真。結果表明:在縱橫向過載指令均為1的條件下,跟蹤誤差近似為0,說明滑模控制策略是解決滾轉導彈非線性控制問題的有效方法之一。

導彈;終端滑模面;滑模變結構控制

Abstract:To analyze the nonlinear control characteristics of rolling missile,according to the simplified nonlinear mode,the sliding mode control method based on the tending law was applied to design the adaptive terminal sliding mode surface including tracking error in acceleration and its integral function,and the state of control system can reach the sliding mode surface and be maintained.To eliminate chattering,the traditional index trending law was placed by the switching function of hyperbolic tangent.According to the stability in the sliding mode motion and dynamic quality,the sliding-mode variable-structure control law was designed.The Simulink simulation on control law was carried out.While the longitudinal and lateral overload is 1g,the tracking error is almost zero.Sliding mode control is one of the effective methods to solve the nonlinear issues of missile.

Keywords:missile;terminal sliding surface;sliding-mode variable-structure control

導彈的運動模型是十分復雜的非線性時變模型,導彈在飛行中以一定的轉速繞縱軸旋轉,會在俯仰與偏航通道之間產生較強的氣動和運動耦合[1]。傳統的控制方法大多忽略其非線性項和耦合項,導致控制性能降低,因此,在飛行控制系統的設計中,應以非線性耦合的模型為對象[2]。

目前,導彈耦合問題的解決方法大致分為2種。一種方法是實現解耦控制[3],解耦的方法包括:特征結構配置、動態逆、神經網絡、魯棒控制等;另一種則是采用耦合補償的方法。文獻[4]針對旋轉炮彈的耦合模型,利用反饋線性化方法得到參數化的滑模控制律并設計參數的自適應律,得到的自適應滑模控制器可以解決耦合,但是存在解耦控制律設計反復等缺點,解耦控制器設計不當或者控制量過大時會導致系統輸出發散。文獻[5]針對大攻角導彈的耦合模型,基于動態反饋補償理論,引入新的輸入變量以抵消非線性耦合因素,進行線性滑模控制。動態反饋補償的解耦方法必須建立在對耦合因素的精確估計并及時進行補償的前提下,否則方法失效。

由此可見,滑模變結構控制(sliding mode control,SMC)存在一定的有效控制范圍。同時,SMC算法的優勢較為明顯,算法簡單,計算負擔較小,且易于工程實現。正因為如此,該算法的研究在各個領域都得到了迅速發展,比如伺服系統[6]、航天器[7]、衛星[8]、斬波器電路[9]和高超聲速飛行器[10]等。

針對導彈經典的線性模型,實現單一通道的SMC控制較為普遍。文獻[11-13]均是針對旋轉導彈的線性模型,設計積分型滑模面或采用指數趨近律的方法,僅實現了俯仰通道的滑模控制,并未涉及偏航方向。

本文針對導彈簡化的非線性模型,完成了俯仰和偏航通道的滑模控制器設計,將傳統的指數趨近律和積分型滑模面[14]相結合并做一些改進工作;將其應用在導彈的滑模控制器設計中,完成基于過載的自動駕駛儀設計,仿真結果表明其跟蹤性能良好。

1 動力學模型

本文研究的導彈為軸對稱型彈體,側滑轉彎(skid to turn,STT)控制,鴨式布局,采用一對“十”字舵面操縱俯仰和偏航運動,通過斜置尾翼來穩定一定的滾轉角速度。采用如下簡化假設:

①攻角和側滑角都為小量,近似視為cosα≈cosβ≈1成立;

②相較其他因素,彈體自身慣性積的影響可以忽略;

③每一個特征點處的各個氣動參數均視為常值;

④模型中的二階小量均忽略不計。

則考慮俯仰與偏航通道間的耦合效應,在準彈體系下建立導彈簡化動力學模型[15]:

(1)

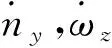
2 滑模控制器設計

設計滑模控制器的目的在于當外界干擾和耦合存在的情況下,保證導彈控制系統的穩定性,實現對指令信號的跟蹤。

導彈以一定的轉速繞縱軸旋轉,導致俯仰和偏航2個通道之間存在氣動耦合。為了實現對簡化的耦合模型的有效控制,往往在導彈的控制器設計中需要分別對俯仰通道和偏航通道進行單獨設計,最后進行雙通道的控制算法仿真。

本文針對導彈的非線性簡化模型,設計雙通道滑模控制器,具體步驟如下:

①將控制模型分為俯仰和偏航2個通道。從俯仰通道控制器的設計入手,忽略模型中的耦合非線性項,將其視為干擾,因此,2個通道可獨立設計滑模控制器。

②按照滑模控制器的設計步驟設計出俯仰通道的滑模控制器。首先選擇合適的滑動超平面,保證滑動模態穩定;然后求取俯仰方向的滑模控制律,以保證系統在有限的時間內到達滑模面。

③單獨對俯仰通道進行控制算法仿真。在仿真的過程中,耦合干擾項的處理方法是先設置常值干擾試探其抗干擾性;然后設置周期干擾,驗證滑動模態,即驗證變結構控制系統中滑模運動發生在切換面上的運動形式對干擾是否具有不變性;選取特征點并對控制器的設計參數進行尋優,直到滑動模態對干擾具有不變性,尋優結束;最終完成俯仰方向滑模控制器的設計。

④單獨設計偏航控制器。設計方法與俯仰完全類似,即重復前3步,設計出偏航方向滿足導彈控制系統性能指標的滑模控制器。

⑤重新推導2個通道的滑模控制律。嚴格按照式(1)所建立的非線性模型,重新推導2個通道含有耦合項的滑模控制律。

⑥進行雙通道控制器的算法仿真,包括完整的耦合模型和重新推導設計的含有耦合項的滑模控制律。由于步驟③通過參數尋優驗證了滑動模態對常值干擾和周期干擾具有不變性,所以在仿真的過程中加入完整的耦合項,設計參數稍做調整,以滿足導彈控制系統的設計要求。

2.1 俯仰通道的滑模控制器設計

本節通過導彈模型中描述縱向運動的狀態變量(縱向過載和俯仰角速度)的信息,完成俯仰通道的滑模控制器的設計。

2.1.1 滑模面的選取

選取合適的滑動超平面,可以保證滑動運動的穩定性和動態品質。根據導彈俯仰通道的數學模型,選擇ny,c,ωz,c為過載和角速度指令信號;選取滑動模態的狀態變量為ny-ny,c,ωz-ωz,c。本文針對傳統積分型滑模面進行改進,其優勢如下:

①采用積分型滑模面,避免了傳統微分型滑模面對很多信號導數難以測量的難題,并且部分信號的導數(比過載的導數)并沒有實際的物理意義。

②積分型滑模面保留了過載積分和過載之間的導數關系,便于SMC控制律的簡化,而且使控制律中不含積分運算,減輕了運算負擔。

③引入過載誤差的積分函數,使過載的跟蹤性能更好。對傳統積分型滑模面進行改進,將含有誤差信號冪次方的積分項設計為終端滑模面,這使系統的快速性大大提高。

④引入積分器,使SMC控制器具有較強的自適應能力,能夠消除系統的未建模誤差等諸多不確定項帶來的靜差。

本文設計終端自適應滑動模態面σpich來描述狀態變量的誤差:

(2)

式中:c1,c2,c3均為小于0的設計參數,并且直接影響誤差收斂到0的時間。c1可以通過極點配置以及最優控制進行選擇;c2,c3可以通過數字仿真,根據模型的動態特性進行選擇和調整。

2.1.2 控制律的求取

變結構控制特性可以迫使系統在一定特性下沿規定的狀態軌跡做小幅度、高頻率的滑模運動。為達到滑模運動的漸進穩定性及良好的動態品質的設計目標,變結構控制律的設計是至關重要的。

導彈的滑模控制律的求取包括3個關鍵點:首先,求得滑模函數的微分表達式;然后,對控制模型進行變換,根據所設計的自動駕駛儀架構中的反饋回路,求得對應回路中反饋量的表達式,將其帶入滑模函數的微分等式中;最后,利用滑模函數的微分形式與所選取的趨近律相等關系,求得滑模控制律。

為了消除變結構控制中的抖振現象,本文采用雙曲正切切換代替符號切換,連續的趨近律如下:

(3)

式中:μ為小量;ρ1,k1為控制器設計參數,均為正數。μ,ρ1,k1可以在數字仿真時根據系統的動態特性進行選擇和設計。

根據式(2)的滑模面,求導可得:

(4)

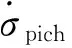
(5)

其中各系數定義如下:

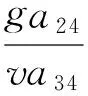
根據式(5)推導的結果,設計變結構控制律:

upich=u1p+u2p

(6)

(7)

(8)

式中:upich為所設計的滑模控制律,u1p為等效控制律,u2p為非線性控制項。

2.2 偏航通道滑模控制器設計

本文的研究對象為導彈,采用STT控制,由于其俯仰通道和偏航通道的模型完全一致,故偏航通道的滑模控制器設計過程與俯仰通道完全類似,在此不再贅述。

2.2.1 滑模面的選取

選擇滑動模態的狀態變量為nz-nz,c,ωy-ωy,c,設計如下自適應終端滑動模態面:

(9)

式中:c4,c5,c6均為小于0的設計參數,調節規則與俯仰通道一致。

2.2.2 控制律的求取

采用連續的趨近律:

(10)

式中:μ為小量;ρ2,k2為控制器設計參數,均為正數。

根據式(9)的滑模面,求導可得:

(11)

將式(1)、式(10)帶入式(11),整理可得:

(12)

其中各系數定義如下:

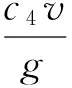
根據式(12)推導的結果,設計變結構控制律:

uyaw=u1w+u2w

(13)

(14)

(15)

式中:uyaw為所設計的滑模控制律,u1w為等效控制律,u2w為非線性控制項。

3 滑模控制器穩定性證明

系統的穩定性關系到控制器設計的性能,本文針對所研究導彈的非線性、強耦合系統(1)進行李雅普諾夫穩定性證明。由于俯仰與偏航2個通道控制器的漸進穩定性證明完全類似,僅以俯仰通道為例。首先,為了后面的穩定性證明的便利,給出引理1,并進行證明。

引理1[17]對于任意給定的x,存在ε>0,存在不等式:

(16)

證明:

根據雙曲正切函數的表達式:

(17)

由于

(18)

可得:

(19)

從而

(20)

即引理1,式(16)成立。證畢。

為證明所設計的滑模控制器的穩定性,構造如下Lyapunov函數:

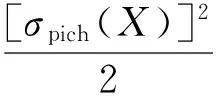
(21)

求導得:

(22)

將滑模面的導數式(5)帶入式(22),得:

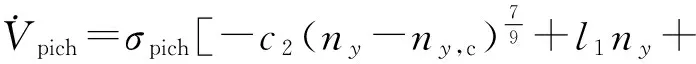
(23)

再將控制律式(6)～式(8)帶入式(23),可得:

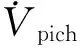
(24)

則式(24)化簡為

(25)

式(25)滿足2個不等式關系:

①已知ρ1,μ為正實數,根據引理1的結論,不等式σpichtanh(μ-1σpich)≥0恒成立,進而不等式-ρ1[σpichtanh(μ-1σpich)]≤0恒成立;

4 仿真分析

為了驗證滑模控制律的正確性,以某型導彈為例,進行俯仰和偏航通道的算法仿真驗算。從飛行彈道中選取某一特征點進行跟蹤仿真,如表1所示,設定導彈飛行速度為222.8 m/s,飛行高度為5 356.6 m。

表1 某特征點的動力系數

仿真結果表明,本文所設計的控制器存在如下兩點限制條件:

①由于導彈實際飛行過程中執行機構存在飽和限制,輸出具有一定的約束范圍,則控制量限制在±18°以內;

②過載指令不能過大,不能超過可用過載。由于過載指令由制導回路給出,存在可用過載小于極限過載的限制。

仿真分別通過輸入2種信號(階躍信號和正弦信號)來分析驗證控制系統的時域性能指標及其跟蹤性能。

4.1 階躍響應

若輸入階躍信號,設置過載指令為2,角速度指令為0。通過仿真尋優選取控制器的設計參數,最終選取:c1=-3.5,c2=-8.5,c3=-1,ρ1=1.4,k1=4,c4=-11,c5=-4,c6=-2.5,ρ2=1.2,k2=2.5,μ=0.5。

圖1為俯仰、偏航的滑模面;圖2為俯仰、偏航的非線性控制律;圖3為等效升降、方向舵偏角曲線;圖4為俯仰、偏航角速度;圖5為縱向、橫向過載的階躍跟蹤曲線。

從圖1～圖5可以看出,控制器僅用0.2 s完成了趨近過程,系統輸出曲線平滑且無超調,響應較快。

從圖1可以看出,滑動模態在仿真開始0.2 s就到達0附近;從圖2可以看出,系統的非線性控制律在0.3 s就達到收斂。通過程序計算,一方面,從其縱向過載的階躍響應可以求得:上升時間tr=0.09 s,峰值時間tp=0.19 s,調節時間ts=0.21 s,最大超調量p=5%,跟蹤誤差為0;另一方面,從其橫向過載的階躍響應可以求得:上升時間tr=0.09 s,峰值時間tp=0.21 s,調節時間ts=0.13 s,基本無超調量,跟蹤誤差為0。

4.2 正弦響應

輸入為正弦信號:ny,c=nz,c=sin0.8πt,控制器設計參數不變,仿真時間為10 s,仿真結果如圖6～圖8所示。圖6為正弦信號下的等效升降、方向舵偏角曲線;圖7為正弦信號下的俯仰、偏航角速度;圖8為縱向、橫向過載的正弦跟蹤曲線。

圖4～圖6說明,系統的跟蹤效果良好,曲線平滑且響應較快,誤差較小。縱向過載的跟蹤誤差在±0.18范圍內;橫向過載的跟蹤誤差為±0.1范圍內。

5 結束語

本文以導彈簡化的非線性模型為研究對象,引入積分型滑模面,設計導彈過載控制系統的自適應滑模控制律,構造Lyapunov函數并進行穩定性證明。在此基礎上,本文采用雙曲正切切換函數代替符號切換函數,有效地消除滑模控制所具有的抖振。在各種干擾下,通過滑模控制律的反復推導,并利用控制參數的尋優,實現俯仰和偏航通道的控制算法仿真。仿真結果表明,本設計具有良好的動態性能和良好的跟蹤性能,為旋轉導彈的控制律設計提供了參考。

[1] 范世鵬,林德福,姚懷瑾,等.基于最優二次型理論的滾轉導彈三回路駕駛儀設計與研究[J].兵工學報,2015,36(5):831-838. FAN Shi-peng,LIN De-fu,YAO Huai-jin,et al.Research on three-loop autopilot for rolling missile based on linear quadratic optimal control theory[J].Acta Armamentarii,2015,36(5):831-838.(in Chinese)

[2] 陳圣,王旭剛.基于浸入與流形不變的制導炮彈非線性自適應控制[J].電光與控制,2014,21(3):18-22. CHEN Sheng,WANG Xu-gang.Nonlinear adaptive control of guided projectile based on immersion and invariance[J].Electric and Control,2014,21(3):18-22.(in Chinese)

[3] 賈杰,劉連章,曹琦.導彈解耦控制方法綜述[J].航空兵器,2010(3):18-21. JIA Jie,LIU Lian-zhang,CAO Qi.Survey on decoupling control methods for missile[J].Aero Weaponry,2010(3):18-21.(in Chinese)

[4] 楊榮軍,楊樺,梁旭棟,等.基于自適應滑模的制導炮彈控制系統設計[J].彈道學報,2012,24(3):75-79. YANG Rong-jun,YANG Hua,LIANG Xu-dong,et al.Control system design for guided projectile based on adaptive sliding mode control[J].Journal of Ballistics,2012,24(3):75-79.(in Chinese)

[5] 羅緒濤,梁曉庚.大攻角導彈DDFC變結構解耦控制器設計[J].計算機仿真,2012,29(7):101-104. LUO Xu-tao,LIANG Xiao-geng.Design of sliding decoupling controller with high angle-of-attack missile based on DDFC[J].Computer Simulation,2012,29(7):101-104.(in Chinese)

[6] 李偉,韓崇偉,位紅軍,等.伺服系統的滑模變結構控制器設計[J].計算機仿真,2011,28(12):5-8. LI Wei,HAN Chong-wei,WEI Hong-jun,et al.Design of sliding mode controller for servo system[J].Computer Simulation,2011,28(12):5-8.(in Chinese)

[7] WANG J,SUN Z.6-DOF robust adaptive terminal sliding mode control for spacecraft formation flying[J].Acta Astronautica,2012,73(2):76-87.

[8] YADEGARI H,HAN C,ZHU Y.Finite time sliding mode controller for a rigid satellite in presence of actuator failure[C]//International Conference on Information Science and Control Engineering.Beijing:IEEE Computer Society,2016:1 327-1 331.

[9] AMET L,GHANES M,BARBOT J P.Direct control based on sliding mode techniques for multicell serial chopper[C]//Proceedings of the 2011 American Control Conference.San Francisco,CA:IEEE,2011:751-756.

[10] HU Z,BO M,ZHOU D,et al.Robust nonlinear control of a hypersonic aircraft based on sliding mode control[J].Procedia Engineering,2012,29:837-842.

[11] 李鵬,孫未蒙,李文強,等.一種改進積分滑模面在飛控中的應用[J].控制工程,2010,17(3):269-271. LI Peng,SUN Wei-meng,LI Wen-qiang,et al.Application of improved integral sliding surface to flight control system[J].Journal of Control Engineering,2010,17(3):269-271.(in Chinese)

[12] 岳明橋,雷軍委,李高鵬.采用一類積分型滑模的導彈控制系統設計[J].航天控制,2010,28(6):29-32. YUE Ming-qiao,LEI Jun-wei,LI Gao-peng.The design of missile system with integral sliding mode control[J].Aerospace Control,2010,28(6):29-32.(in Chinese)

[13] CHENG H,DONG C,WANG Q.Integrated guidance and control backstepping design based on integral sliding mode surface for missiles[C]//Control Conference.Nanjing:IEEE,2014:573-578.

[14] 劉藝寧,郭建國,周軍,等.高超聲速飛行器積分型Terminal滑模控制設計[J].電光與控制,2014,21(12):67-70. LIU Yi-ning,GUO Jian-guo,ZHOU Jun,et al.Design of integral type terminal sliding mode controlling method for hypersonic vehicle based on disturbance observer[J].Electric and Control,2014,21(12):67-70.(in Chinese)

[15] 王旭剛,荊琴.制導彈藥方案彈道跟蹤與控制[J].計算機仿真,2011,28(2):62-66. WANG Xu-gang,JING-Qin.Precise trajectory tracking and control for guided projectile using acceleration guidance logic[J].Computer Simulation,2011,28(2):62-66.(in Chinese)

[16] 錢杏芳,林瑞雄,趙亞男.導彈飛行力學[M].北京:北京理工大學出版社,2013. QIAN Xing-fang,LIN Rui-xiong,ZHAO Ya-nan.Missile fight dynamics[M].Beijing:Beijing Institute of Technology Press,2013.(in Chinese)

[17] AGHABABA M P,AKBATI M E.A chattering-free robust adaptive sliding mode controller for synchronization of two different chaotic systems with unknown uncertainties and external disturbances[J].Applied Mathematics & Computation,2012,218(9):5 757-5 768.

DesignonSlidingModeControllerofMissileBasedonTerminalSlidingModeSurface

HUA Si-yu,WANG Xu-gang

(School of Energy and Power Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)

2017-04-05

軍工“十三五”預研項目

華思雨(1992- ),女,碩士研究生,研究方向為飛行動力學與控制。E-mail:Rain_HSY@163.com。

王旭剛(1979- ),男,副研究員,博士,研究方向為飛行動力學、制導與控制。E-mail:wxgnets@163.com。

TJ765.2

A

1004-499X(2017)03-0020-07