不同優化算法在輪式自行火炮動力學優化中的應用

曹巖楓,牛福強,2,洪亞軍,徐 誠

(1.南京理工大學 機械工程學院,江蘇 南京 210094;2.陸軍軍官學院 炮兵系,安徽 合肥 230031; 3.上海航天技術研究院805所,上海 201108)

不同優化算法在輪式自行火炮動力學優化中的應用

曹巖楓1,牛福強1,2,洪亞軍3,徐 誠1

(1.南京理工大學 機械工程學院,江蘇 南京 210094;2.陸軍軍官學院 炮兵系,安徽 合肥 230031; 3.上海航天技術研究院805所,上海 201108)

以某輪式自行火炮為例,以減少炮口初始擾動、提高射擊精度為目標,建立了基于輪式自行火炮發射動力學仿真的優化設計模型。采用加權組合法將炮口角位移與角速度統一為單目標,分別應用序列二次規劃法、粒子群算法、模擬退火算法及多島遺傳算法對其進行優化設計求解。比較結果發現,模擬退火算法及多島遺傳算法能夠適應輪式自行火炮系統優化問題的求解需求;粒子群算法盡管收斂速度較快,但優化結果不如模擬退火算法及多島遺傳算法;序列二次規劃法由于容易陷入局部最優,不能適應輪式自行火炮系統優化問題的求解需求。

輪式自行火炮;發射動力學;動力學優化;總體參數優化

Abstract:To reduce the initial muzzle disturbance and increase the shooting accuracy of wheeled self-propelled gun,an optimization model was built based on the firing dynamics model of self-propelled gun.The muzzle angular-displacement and angular-velocity were normalized to a single target by weighted method.The model was optimized respectively by NLPQL,PSO,ASA and MIGA.The simulation results show that ASA and MIGA can meet the demand of the optimization problem of the wheeled self-propelled gun system.Although the convergence speed is quicker,the optimization result of PSO is not as good as that of ASA and MIGA.Because it is easy to fall into local optimum,NLPQL cannot adapt to the demand of the optimization problem of wheeled self-propelled gun system.

Keywords:wheeled self-propelled gun;firing dynamics;dynamics optimization;conceptual parameters optimization

火炮射擊精度是火炮最重要的戰術技術指標之一。炮口的初始擾動、彈丸制造誤差以及氣象條件等都會對射擊精度產生影響。在這些因素中,炮口初始擾動對射擊精度的影響較大。因此,要提高輪式自行火炮的射擊精度,必須對火炮系統發射時的運動以及受力規律進行研究,以獲得彈丸飛離炮口瞬間炮口的線位移、線速度、角位移、角速度等運動參數與輪式自行火炮總體參數間的關系,并通過優化的方法尋求各總體參數間更優的匹配關系來減少炮口初始擾動,改善輪式自行火炮的射擊精度,提高綜合特性。

國內外一直非常重視自行火炮動力學優化研究,已經獲得了大量研究成果。毛保全等[1-2]建立了自行火炮總體結構優化模型,進行了總體參數動力學研究,獲得了較好的優化結果。梁傳建、楊國來等[3]研究了火炮結構動力學優化問題。近年來以智能優化算法為代表的全局優化算法,包括遺傳算法、模擬退火算法、粒子群算法、神經網絡算法和禁忌算法等,發展快速,并在工程上得到了廣泛應用。但目前采用不同優化算法對輪式自行火炮動力學優化進行適用性分析的對比研究較少。本文以減少炮口初始擾動、提高射擊穩定性為目標,基于輪式自行火炮發射動力學仿真模型建立了輪式自行火炮總體參數優化設計模型,分別應用序列二次規劃法(NLPQL)、粒子群算法(PSO)、模擬退火算法(ASA)及多島遺傳算法(MIGA)對其進行優化設計求解,比較研究了幾種優化算法針對輪式自行火炮優化設計問題的適應能力。

1 輪式自行火炮發射動力學仿真模型的建立

1.1 模型簡化

輪式自行火炮是一個結構、運動以及受力情況十分復雜的系統,完全如實地描述系統非常困難,只能將其實際結構與受力情況進行簡化,在較為理想的模型上進行仿真計算[4]。為此,對模型作如下假設:

①輪式自行火炮在停止狀態下發射;

②模型由底盤、炮塔、搖架、后坐部分以及8個輪胎等12個剛體組成;

③模型共有18個自由度,后坐部分沿搖架做單自由度直線運動,搖架圍繞火炮耳軸做單自由度轉動,炮塔相對底盤做兩自由度轉動,底盤沿3個坐標軸平動,底盤繞3個坐標軸轉動,8個輪胎垂直振動。

1.2 發射動力學方程

發射動力學方程的一般形式:

式中:M為質量矩陣,C為阻尼矩陣,K為剛度矩陣,F為廣義力矩陣,X為廣義坐標。

本文中,X為18×1列陣,元素分別與模型的18個自由度對應;F為18×1列陣;M,C,K均為18×18階方陣。

1.3 發射動力學仿真模型

基于以上對模型的簡化及多體發射動力學理論,在多剛體動力學仿真軟件ADAMS中建立參數化的輪式自行火炮發射動力學模型,如圖1所示。

模型參數化設計變量包括各剛體質量及轉動慣量參數、各剛體空間相對位置參數、各懸掛裝置支撐點相對底盤質心的位置參數、各剛體間連接部分及懸掛裝置的剛度系數和阻尼系數、反后坐裝置結構和性能參數,共計39個。m2,m3分別為炮塔和搖架的質量;xH,yH分別為炮塔質心相對于底盤質心在x和y方向上的距離;xQ,yQ分別為搖架耳軸中心相對于炮塔質心在x和y方向上的距離;xG,yG分別為后坐部分質心相對于搖架耳軸中心在x和y方向上的距離;xLi,yL,zLi為第i排輪胎懸掛裝置與底盤連接點相對底盤質心在x,y,z方向上的距離;k,c分別為懸掛裝置等效彈簧的剛度系數和阻尼系數;k21,c21分別為炮塔與底盤間等效彈簧的剛度系數和阻尼系數;k32,c32分別為搖架與炮塔間等效彈簧的剛度系數和阻力系數;d1,…,d9為節制桿結構參數;AOMG為反后坐裝置支流最小截面積;dP為節制環直徑,dT為駐退活塞直徑,dXT為駐退桿外直徑;AP為復進機活塞工作面積;lXO為復進機容積相當長度;pF0為復進機初壓;AFJ為駐退桿內截面積。

采用該模型對某輪式自行火炮進行發射動力學響應計算,獲得的結果如圖2所示,圖中θ,ω分別為炮口垂直角位移和垂直角速度。計算炮口的最大垂直角速度為0.145 rad/s,該輪式自行火炮試驗獲得的炮口最大垂直角速度為0.141 rad/s,計算結果與實驗結果基本一致,證實了本節所建立的模型的合理性。

2 輪式自行火炮動力學優化設計模型

2.1 優化設計數學模型

炮口初始擾動可以認為是系統結構本身引起的主運動和隨機因素引起的小擾動的疊加。因此,減少因系統結構本身引起的炮口初始擾動主運動部分,將能夠提高系統的射擊精度。衡量炮口初始擾動的主要指標是炮口角位移和角速度。因此,選擇彈丸出膛口瞬間的垂直角位移和垂直角速度為目標函數,對火炮結構參數進行優化,達到提高射擊精度的目的。

1)目標函數。

通過加權得到一個綜合目標函數:

式中:θ0,ω0分別為初始炮口垂直角位移與垂直角速度;θ,ω分別為優化過程中的炮口垂直角位移和垂直角速度;w1,w2分別為角位移和角速度的權系數,滿足:w1+w2=1,w1>0,w2>0。

2)設計變量。

優化模型的設計變量即為發射動力學模型中參數化的設計變量,共39個。

3)約束條件。

約束分為設計變量約束和狀態變量約束。其中設計變量約束上、下限根據經驗確定。由于設計變量較多,在此不一一列出,只給出狀態變量約束,如下:

①總質量m應不大于火炮質量m0指標,即m≤m0。

②后坐阻力須加以峰值約束條件,以避免設計的反后坐裝置所產生的后坐阻力超過一定值而影響火炮的射擊穩定性,即

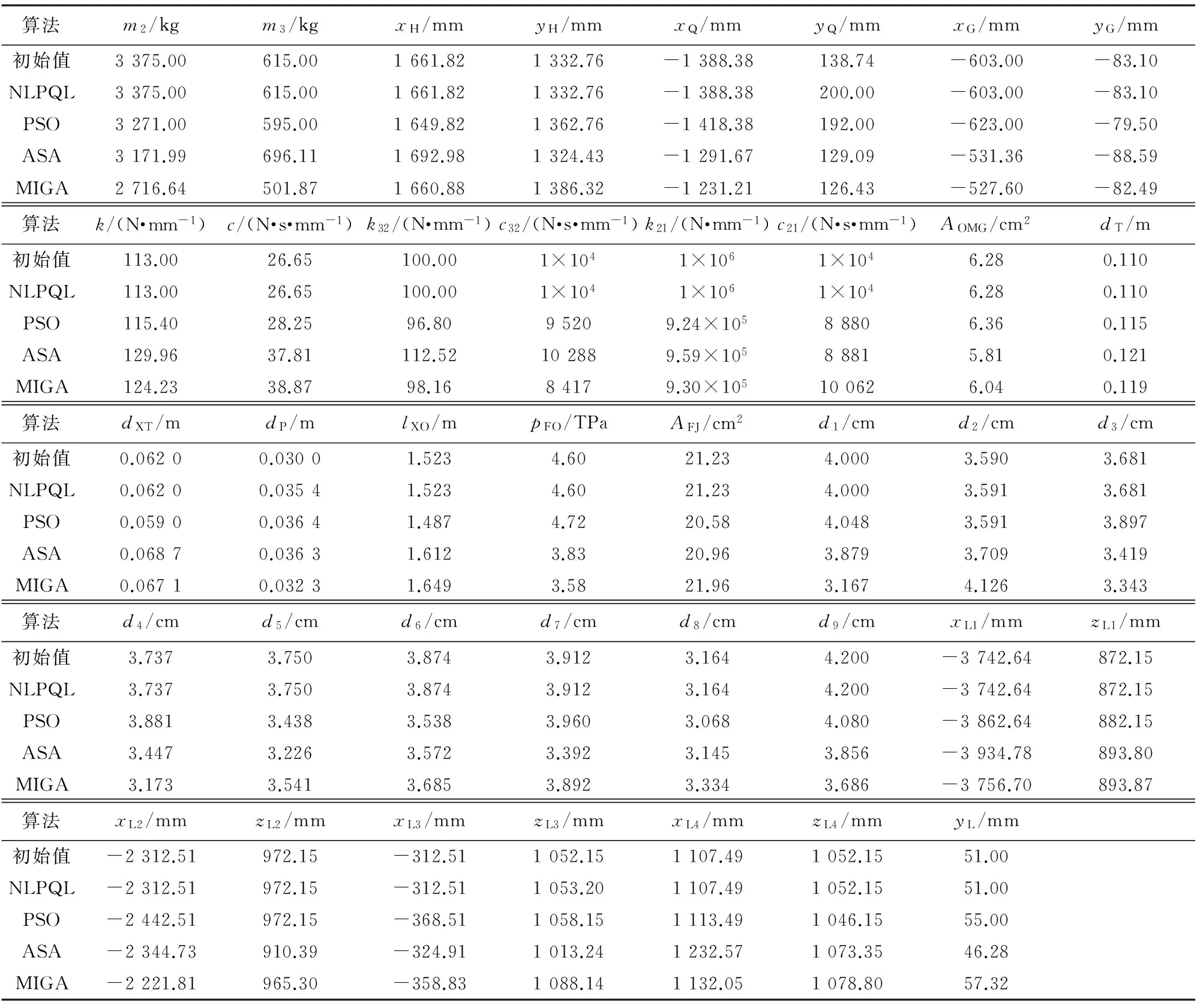
maxFR(t)

式中:FR0為后坐阻力平均值。

2.2 優化設計流程

輪式自行火炮發射動力學優化流程:

①輸入基準總體方案和參數(初始方案);

②進行輪式自行火炮發射動力學計算、質量計算、后坐阻力計算,預測設計方案技術指標值;

③判斷優化目標函數是否達到收斂,若收斂,結束,輸出優化方案和參數;若不收斂,轉向②,按智能優化算法更新迭代狀態,進行設計空間搜索和迭代。

3 優化設計結果

采用加權組合法將炮口垂直角位移與垂直角速度統一為優化目標,分別應用序列二次規劃法(NLPQL)、粒子群算法(PSO)、模擬退火算法(ASA)及多島遺傳算法(MIGA)對其進行優化設計求解。優化收斂歷程如圖4～圖7所示,圖中,n為迭代步數,優化結果如表1和表2所示。

優化算法J優化前優化后ΔJ/%NLPQL10.991PSO10.82417.6ASA10.57642.4MIGA10.62237.8

表2 參數優化結果

由圖4及表1、表2可以看出,采用序列二次規劃法(NLPQL)進行優化時,目標函數很快就到達了局部最優,不能夠適應較為復雜的輪式自行火炮優化問題的求解需求。

由圖5～圖7及表1、表2可以看出,模擬退火算法在2 000步后收斂,優化后目標函數提高了42.4%;多島遺傳算法尋優需要更長計算時間,在6 000步后收斂,優化后目標函數提高了37.8%;粒子群算法在迭代300步開始收斂,但最終優化目標函數提高了17.6%,也有一定的優化效果。模擬退火算法和多島遺傳算法更能夠適應輪式自行火炮系統優化問題的求解需求。

雖然序列二次規劃法等局部優化算法有著容易陷入局部最優的缺點,但其在局部收斂速度較快,可與其他全局優化算法組合使用,提高優化效率。

4 結束語

本文建立了輪式自行火炮發射動力學仿真模型和輪式自行火炮動力學優化設計模型,分別應用序列二次規劃法(NLPQL)、粒子群算法(PSO)、模擬退火算法(ASA)及多島遺傳算法(MIGA)對其進行優化設計求解。計算結果表明,本文建立的輪式自行火炮動力學優化設計模型是合理的,4種優化算法中模擬退火算法(ASA)與多島遺傳算法(MIGA)對求解輪式自行火炮系統優化問題的適應性較好。

[1] 毛保全,穆歌.輪式自行火炮總體結構參數的優化設計研究[J].兵工學報,2003,24(1):5-8. MAO Bao-quan,MU Ge.Optimal design of the structural parameters[J].Acta Armamentarii,2003,24(1):5-8.(in Chinese)

[2] 毛保全,邵毅.火炮自動武器優化設計研究[M].北京:國防工業出版社,2007. MAO Bao-quan,SHAO Yi.Optimization of gun automatic weapon[M].Beijing:National Defense Industry Press,2007.(in Chinese)

[3] 梁傳建,楊國來,王曉峰.基于神經網絡和遺傳算法的火炮結構動力學優化[J].兵工學報,2015,36(5):789-794. LIANG Chuan-jian,YANG Guo-lai,WANG Xiao-feng.Structural dynamics optimization of gun based on neural networks and genetic algorithms[J].Acta Armamentarii,2015,36(5):789-794.(in Chinese)

[4] 張相炎,鄭建國,楊軍榮.火炮設計理論[M].北京:北京理工大學出版社,2005. ZHANG Xiang-yan,ZHENG Jian-guo,YANG Jun-rong.Theory of gun design[M].Beijing:Beijing Institute of Technology Press,2005.(in Chinese)

StudyonDifferentOptimizationAlgorithmsforOptimizationDesignofWheeledSelf-propelledGunFiringDynamics

CAO Yan-feng1,NIU Fu-qiang1,2,HONG Ya-jun3,XU Cheng1

(1.School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China; 2.Department of Artillery,Army Officer Academy,Hefei 230031,China; 3.805 Institute,Shanghai Academy of Spaceflight Technology,Shanghai 201108,China)

2016-11-14

國家自然科學基金項目(51575279)

曹巖楓(1988- ),男,博士研究生,研究方向為復雜機械系統建模、仿真與優化。E-mail:caoyf2010@163.com。

TJ302

A

1004-499X(2017)03-0087-05