歸類題型 總結經驗
——將類比思維運用到高中數學解題教學
徐 佳
歸類題型 總結經驗
——將類比思維運用到高中數學解題教學
徐 佳
高中數學解題教學當中運用到的思維方法有很多,類比思維就是其中最重要的思維方法之一。本文從運用類比思維將新舊知識相聯結與運用類比思維提升探究能力這兩方面對類比思維在高中數學解題教學中的運用進行了探究。
高中數學;解題教學;類比思維;經驗;探究能力
類比思維方法就是對兩個或者兩個以上的事物展開比較,找出它們之間存在哪些相似的地方,并將其作為根據,推出它們在其他方面類似的地方,或者對它們的特征進行綜合比較。類比思維有兩種含義:一是聯想,就是通過接觸的新的知識引發對之前學過知識的回憶;二是類比,將新的知識與舊的知識進行比較,找出它們之間相似的地方與有差異的地方,也就是“異中求同”以及“同中求異”。將類比思維運用到高中數學解題過程當中,能夠激發受教育者的學習熱情與積極性,有助于加深他們對知識的記憶,在解決數學問題的時候充分地發揮理解能力、分析問題的能力及推理能力。
一、 運用類比思維將新舊知識相聯結
若想令受教育者的創新思維得到開發,第一步就是要奠定好根基,豐富他們的知識儲量。在進行數學教學的過程中,要注重新舊知識的聯系,在新知識與舊知識的相互類比當中理解得更加深入,令思維得到拓展。
例如:在對數列這一內容進行講授的時候,因為等比數列與等差數列,不管在定義還是通項公式上都十分類似,容易被混淆。所以在解題的時候可采用類比思想。首先對它們的定義進行比較,一個同減相關,一個同除相關;而從通項公式來看,一個形式是和,一個形式是積。這個時候教育者引導受教育者運用類比思維對和與差、商與積進行思考,引導他們結合等差數列的有關性質展開思維,并聯系等比數列,如下題。
|an|和|ab|成等差數列,性質有:如果m+n=p+q,那么am+an=ap+aq;|an+k|,|an+bn|仍舊成等差數列。在解答這道題的時候,可運用類比思維,得出:|an|,|bn|成等比數列,性質有:如果m+n=p+q,那么am·an=ap·aq;|k·an|(k≠0),|an·bn|依然成等比數列等。如此一來,令受教育者對新知識的學習更親近,有一種熟悉的感覺,不僅令教學內容更加深刻,而且令他們養成了嚴謹的學習習慣。在解決正弦函數與余弦函數的圖像和性質、橢圓與雙曲線相關性質等問題的時候,也能夠運用這種類比思維。
二、 運用類比思維提升探究能力
在解題過程當中運用類比思維不僅能夠提升受教育者的興趣以及學習的成效,還能夠提升他們的探究問題的能力與創新能力,通過將知識展開,令他們更深入地掌握知識,在日后解題的時候,能夠舉一反三、觸類旁通,令他們從“學會知識”到“會學知識”并予以運用。
例如:已經知道圓C:(x-3)2+(y-2)2=4,如果直線mx-y+3=0同圓C相交,交點為M和N。已知∠MCN≥120°,那么請試著對實數m的取值范圍進行計算。所以在課下作業當中布置了如下這道題:已知圓C:(x-3)2+(y-2)2=4,如果直線mx-y+3=0同圓C相交于M和N,已知CM·CN≤-2,那么試著求出實數m的取值范圍。就解題情況來看,依舊有很多受教育者出現了問題,在對這道題進行講解時,教育者應當引導他們找到與這道題相似的習題,令他們運用類比思維進行比較,很快便領悟到了自身存在的問題并找到了解題方法。
再如:在平面直角坐標系xOy中,已經知道圓x2+y2=4上面有四個點到直線12x-5y+c=0之間的距離是1,請對實數c的取值范圍進行計算。
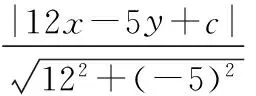
在講解完這道題之后,再延伸出一道類似的探究題:在平面直角坐標系xOy當中已經知道圓C:(x-a)2+(y-b)2=r2(r>0)與直線l:Ax+By+C=0,試著對圓C到直線l的距離為m的點P的數量進行探究。
受教育者們因為剛剛解答過前面的問題,因此探究的熱情極高,他們逐漸有了解題思路并摸索到了解題方法,沉浸在解題的喜悅之中。他們的解題過程如下:
解析:第一步,先思考平面xOy里到直線l:Ax+By+C=0的距離為m的點P應當位于同l平行的兩條直線l1與l2之上,將圓心C與直線l之間的距離設為d,那么:當r
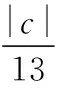
在探究性的解題當中運用類比思維,能夠令受教育者們養成發散思維,能夠增加他們運用數學的意識,提升對數學問題的解決能力。
三、 結束語
綜上所述,在高中數學的解題教學當中善于將相似或者相近概念、圖形或者運算的題型相比較相結合,運用類比思維進行解題,不僅能夠提升教學成效,還能夠令受教育者們養成類比思維,思維得到拓展,探究能力得到提升,同時提升解題能力。
[1]胡紅.類比思維在高中數學教學和解題中的運用[J].新課程學習:中,2013,(7):46.
[2]倪興龍.類比思維在高中數學教學和解題中的運用考述[J].語數外學習:數學教育,2013,(2).
徐佳,江蘇省常熟市王淦昌中學。

