基于二階滑模算法的船舶航向控制

劉勇，卜仁祥，孫大銘

（大連海事大學(xué) 航海學(xué)院，大連 116026）

基于二階滑模算法的船舶航向控制

劉勇，卜仁祥，孫大銘

（大連海事大學(xué) 航海學(xué)院，大連 116026）

針對非線性、易受外界擾動的欠驅(qū)動船舶航向控制系統(tǒng)，基于滑模控制算法的理念，直接對二階航向控制系統(tǒng)中的控制輸入進行設(shè)計，提出一種二階滑模控制算法，通過設(shè)計合理的李雅普諾夫函數(shù)及利用其穩(wěn)定性理論對系統(tǒng)的穩(wěn)定性進行了分析，并利用“育龍”輪運動數(shù)學(xué)模型進行計算機模擬仿真，驗證了該控制算法的合理性及有效性。該算法避免了計算中的維數(shù)膨脹問題，無需對不確定的外界攝動進行定性估計，可以保證閉環(huán)控制系統(tǒng)的漸近收斂及穩(wěn)定。仿真結(jié)果表明，根據(jù)該控制算法所設(shè)計的控制器，能夠有效解決非線性航向控制系統(tǒng)中存在的抖振、超調(diào)以及不能在有限時間內(nèi)快速收斂的問題，而且對外界干擾以及系統(tǒng)攝動不敏感、具有強魯棒性，具有很好的實踐應(yīng)用價值。

欠驅(qū)動船舶；船舶航向控制；二階滑模

常規(guī)水面船舶的控制系統(tǒng)具有欠驅(qū)動特性［1］以及非完整約束特點［2］，模型的非線性［3］、不確定性［4］和易受外界干擾等特點［5］。

針對航向控制問題，劉程［6］等設(shè)計了一種自適應(yīng)模糊跟蹤控制算法，確保了閉環(huán)控制系統(tǒng)的穩(wěn)定性，同時能夠使得航向的跟蹤誤差任意小。朱齊丹［7］等針對船舶航向控制系統(tǒng)中參數(shù)不確定性和外界干擾隨機性的特點，將反步法和非線性滑模觀測器相結(jié)合，設(shè)計了一種能夠保證閉環(huán)系統(tǒng)全局漸近穩(wěn)定的控制算法。李蕓［8］等針對船舶易受不確定的外界干擾的特性，將非線性干擾觀測器的設(shè)計原理和擴張狀態(tài)觀測器可以抑制狀態(tài)干擾的特性相結(jié)合，設(shè)計出一種新的擴張干擾觀測器，有效的減少了滑模控制的抖動影響，同時對干擾具有良好的抑制性能。

二階滑模控制算法作為高階滑模控制算法中的特殊情形，具有設(shè)計簡潔、有限時間收斂、魯棒性強、對外界干擾及系統(tǒng)攝動不敏感的諸多優(yōu)點，同時能夠有效地削弱傳統(tǒng)一階滑模中存在的“抖振”現(xiàn)象，因此受到國內(nèi)外諸多學(xué)者的青睞。針對滑模控制算法，Modirrousta，A［9］等提出一種二階滑模控制算法，該算法對外界干擾不敏感，具有很強的魯棒性，有效解決了系統(tǒng)抖振問題。Zhou［10］等提出一種二階滑模控制算法應(yīng)用到導(dǎo)彈控制系統(tǒng)中，有效解決了系統(tǒng)抖振問題并且使系統(tǒng)迅速準確的進行了目標的跟蹤。Shtessel，Y［11］等設(shè)計了一種自適應(yīng)滑模控制器，仿真結(jié)果軌跡平滑、跟蹤準確，可以有效的應(yīng)對不確定的外界因素的干擾。Shtessel，Y［12］等為一階和二階動態(tài)控制系統(tǒng)設(shè)計了一種二階滑模控制算法，可以確保系統(tǒng)在有限的時間內(nèi)收斂，跟蹤準確，控制效果良好。Levant［13-14］在文獻中系統(tǒng)地闡述了二階滑模控制方法，并對二階滑模控制算法的設(shè)計原則進行了詳細的表述。隨后，在文獻中提出了基于輸出反饋控制的高階滑模控制算法。李雪冰［15］等將加冪積分技術(shù)應(yīng)用到傳統(tǒng)的二階滑模算法中，設(shè)計了一種新的二階滑模控制算法，利用倒立擺控制系統(tǒng)驗證了系統(tǒng)可以在有限時間內(nèi)穩(wěn)定。袁贛南［16］等為了削弱傳統(tǒng)滑模控制系統(tǒng)中存在的抖振現(xiàn)象以及簡化二階滑模控制器的設(shè)計過程，提出一個二階滑模控制系統(tǒng)的滑模到達的有效條件，結(jié)果表明能有效抑制控制系統(tǒng)中的抖振，具有很強的魯棒性和良好的控制性能。

本文針對欠驅(qū)動船舶非線性航向控制系統(tǒng)，運用滑模控制思想，提出一種二階滑模控制算法，并利用該算法設(shè)計二階滑模控制器。利用“育龍”輪操縱運動數(shù)學(xué)模型，針對在不同外界干擾下的航向階躍響應(yīng)進行了仿真，結(jié)果表明控制器對不確定的外界干擾以及系統(tǒng)的攝動不敏感，算法具有很強的魯棒性和良好的控制性能，有效的減弱了系統(tǒng)的抖振和解決了航向不能快速穩(wěn)定問題。

1 二階滑模控制算法

1.1 問題的描述

考慮以下單輸入單輸出控制系統(tǒng)：

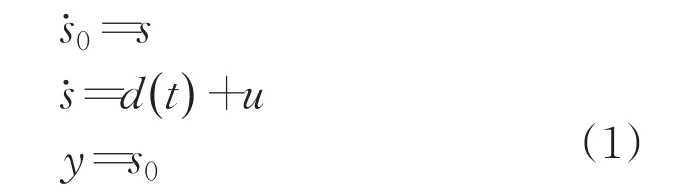
式中，s∈Rn為狀態(tài)變量，u∈R為控制輸入，d(t)為不確定的外界干擾，y為系統(tǒng)輸出。

對于系統(tǒng)（1）而言，控制系統(tǒng)的設(shè)計目標是設(shè)計合理的二階滑模控制算法，使上述系統(tǒng)在外界干擾和系統(tǒng)攝動不確定的情況下能夠達到漸進穩(wěn)定。

1.2 二階滑模控制算法

滑模控制的優(yōu)點是能克服系統(tǒng)的不確定性，對不確定的外界干擾和未建模動態(tài)具有很強的魯棒性，尤其是對非線性系統(tǒng)具有良好的控制性能和效果。對于系統(tǒng)（1），控制的目標為設(shè)計合理的控制輸入u，使狀態(tài)變量在有限的時間內(nèi)收斂并穩(wěn)定。

本文設(shè)計的二階滑模控制算法如下：

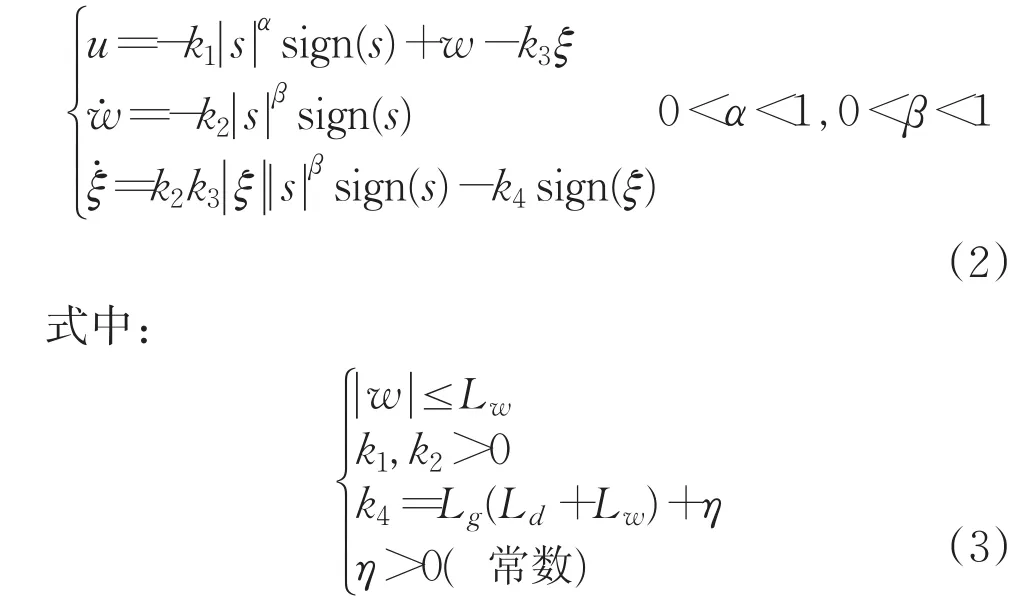
將式（2）代入到系統(tǒng)（1）中，得：

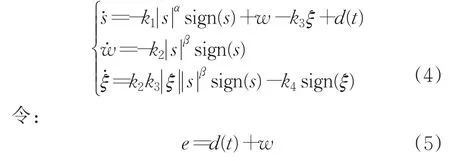
式（4）可以寫為：

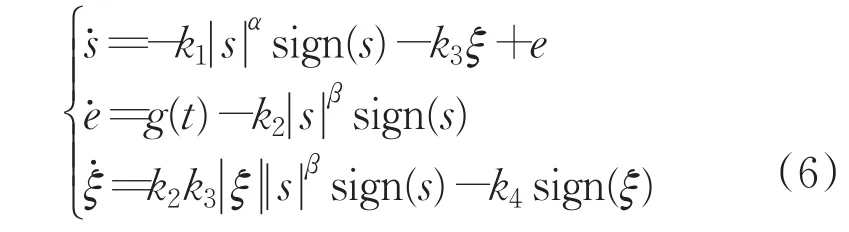
李亞普諾夫函數(shù)設(shè)計如下：

系統(tǒng)穩(wěn)定性分析如下：

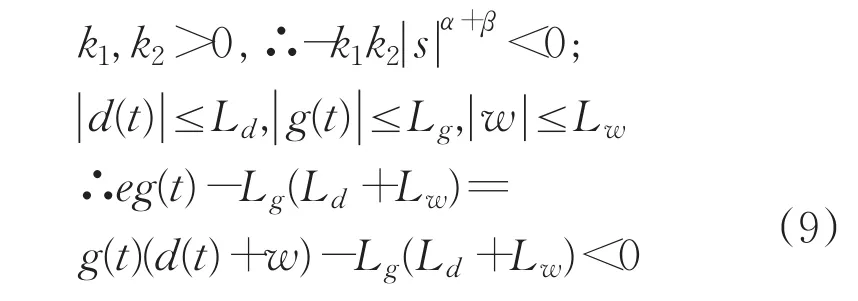
根據(jù)式（9）得：

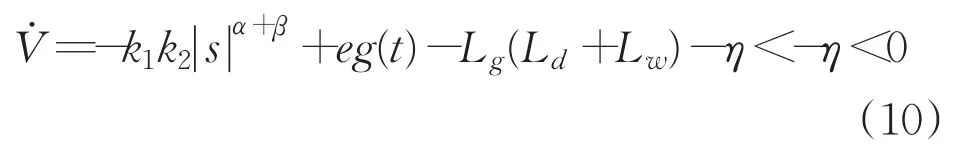
因為V＞0且所以系統(tǒng)漸進穩(wěn)定。

2 基于二階滑模算法的航向控制器的設(shè)計及仿真

2.1 船舶航向控制問題

對于非線性航向控制系統(tǒng)：

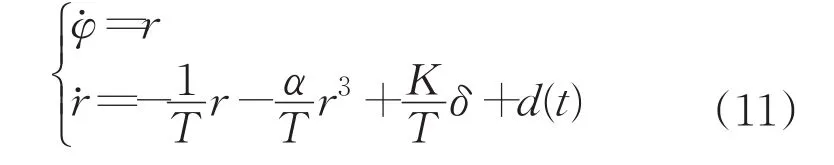
其中，φ為航向，r為轉(zhuǎn)首角速度，K,T為有界的船舶參數(shù)，α為非線性項參數(shù)，d(t)為連續(xù)的外界干擾，δ為舵角。

船舶非線性航向控制問題為：確定δ，使φ→φd及r→0，φd為計劃航向，通過坐標轉(zhuǎn)換及平移，控制問題可簡化為使φ→0。

舵機響應(yīng)模型［2］一般為：

其中，δr為命令舵角，TE為舵機時間常數(shù)。

2.2 船舶航向二階滑模控制算法

對于系統(tǒng)（11），令：

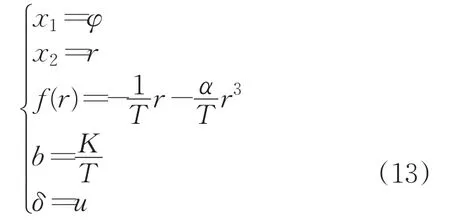
非線性航向控制系統(tǒng)（11）可轉(zhuǎn)化為：

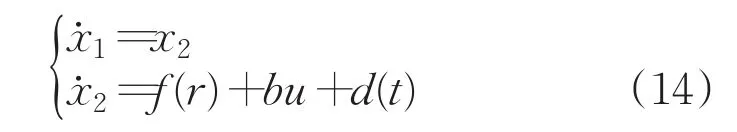
因此，非線性航向控制系統(tǒng)（11）及系統(tǒng)（14）的二階滑模控制算法為：

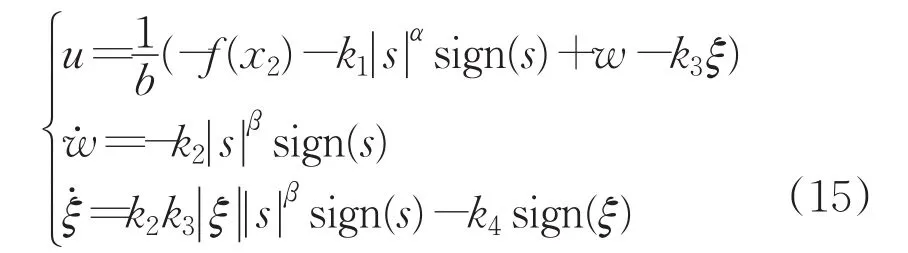
通過設(shè)計此控制律使得系統(tǒng)在外界干擾不確定的情況下，保持系統(tǒng)穩(wěn)定收斂的不變性，具有很強的魯棒性和很好控制效果。

2.3 船舶航向控制仿真與分析

為驗證本文設(shè)計的控制算法的有效性及對船舶航向的控制效果，運用MATLAB的Simulink仿真環(huán)境設(shè)計船舶運動數(shù)學(xué)模型（11）及船舶航向控制程序，對控制器中各參數(shù)進行合理的設(shè)計，并以“育龍”輪為對象，其中K=0.478，T=216，α=30，針對不同外界干擾情況下控制器的控制品質(zhì)進行計算機模擬仿真，并進行了相應(yīng)的對比分析。

仿真過程中，程序中各參數(shù)設(shè)置如下：k1=1；k2=0.01；k3=0.1；k4=1。將二階滑模控制算法轉(zhuǎn)化為程序，引入到航向控制器中，得到控制輸入，實現(xiàn)閉環(huán)系統(tǒng)的穩(wěn)定、準確跟蹤。對于外界干擾的設(shè)置，本文將外界干擾直接設(shè)置在船舶模型里面，來驗證控制器的強魯棒性以及對外界攝動的不敏感性。

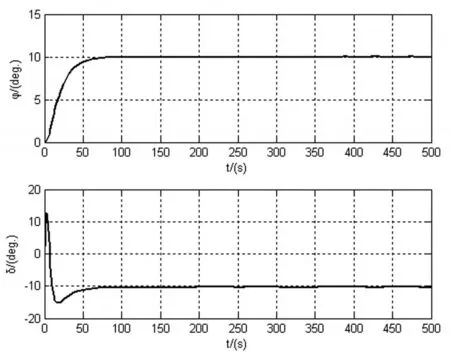
圖1 無干擾時航向改變10°的仿真結(jié)果

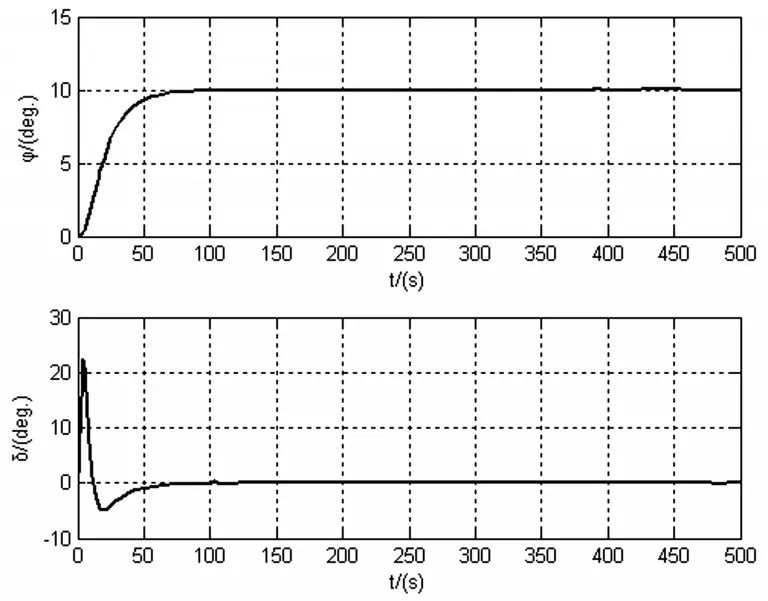
圖2 有外界干擾時航向改變10°仿真結(jié)果

圖1表明航向的仿真曲線平滑、跟蹤穩(wěn)定準確，超調(diào)和抖振很小，舵角曲線有一定的超調(diào)符合航海實際。船舶進行轉(zhuǎn)向的時候，為了防止船舶運動軌跡出現(xiàn)頻繁的“S”形，舵角需要提前進行相應(yīng)的壓舵調(diào)節(jié)來控制轉(zhuǎn)首角速率和航向偏差，使得船首迅速而準確的穩(wěn)定，結(jié)果表明控制器在無外界干擾的情況下具有良好的控制品質(zhì)。

圖2表明航向仿真曲線在有外界干擾的情況仍然平滑、跟蹤穩(wěn)定準確，超調(diào)和抖振很小。不同的是舵角曲線，在有外界干擾的情況下，船舶需要進行較大的舵角來抵抗外界干擾，來確保船舶航向的快速響應(yīng)和穩(wěn)定，結(jié)果表明控制器對外界干擾的擾動不明顯，具有很強的魯棒性。

3 結(jié)論

本文針對欠驅(qū)動船舶非線性航向控制系統(tǒng)，利用滑模控制思想，直接設(shè)計航向控制系統(tǒng)的控制輸入，提出一種新的二階滑模控制算法，利用李亞普諾夫穩(wěn)定性理論證明了系統(tǒng)的穩(wěn)定，設(shè)計的二階滑模船舶航向控制器，可以確保航向控制系統(tǒng)在有限時間內(nèi)穩(wěn)定收斂。

本文設(shè)計的二階滑模控制算法計算量較少，有效的避免了傳統(tǒng)滑模控制計算中容易出現(xiàn)的“維數(shù)膨脹”問題。利用本文提出的控制算法所設(shè)計的控制器對外界干擾等不確定因素的攝動不敏感，具有很強的魯棒性和良好的控制效果。控制算法很好的削弱了二階航向控制系統(tǒng)中超調(diào)和抖振問題。

［1］Mahmut，Arjan，Harris N.Dynamics and control of a class of underactuated mechnical systems［J］.IEEE Transactions on Automatic Control，1999，44（9）：1663-167l.

［2］卜仁祥.欠驅(qū)動水面船舶非線性反饋控制研究［D］.大連：大連海事大學(xué)，2008.

［3］李鐵山，楊鹽生，鄭云峰.不完全驅(qū)動船舶非線性控制［J］.交通運輸工程學(xué)報，2003，3（4）：39-43.

［4］郭晨，汪洋，孫富春，等.欠驅(qū)動水面船舶運動控制研究綜述［J］.控制與決策，2009（03）：321-328.

［5］卜仁祥，劉正江，胡江強.基于動態(tài)非線性滑動模態(tài)的欠驅(qū)動船舶直線航跡控制［J］.清華大學(xué)學(xué)報：自然科學(xué)版，2007（S2）：1880-1883.

［6］劉程，李鐵山，陳納新.帶有舵機特性的船舶航向自動舵DSC-MLP設(shè)計［J］.哈爾濱工程大學(xué)學(xué)報，2012，33（01）：9-14.

［7］朱齊丹，周芳，趙國良，等.基于反步法和滑模觀測器的船舶航向控制［J］.華中科技大學(xué)學(xué)報：自然科學(xué)版，2009，37（04）：122-125.

［8］李蕓，白響恩，肖英杰.基于新型擴張干擾觀測器的船舶航向滑模控制［J］.上海交通大學(xué)學(xué)報，2014，12（48）：1708-1713.

［9］Modirrousta A，Sohrab M，Dehghan S.A modified guidance law for ground moving target tracking with a class of the fast adaptive second-order sliding mode［J］.Transactions of the Institute of Measurement and Control，2016，38（07），819-831.

［10］Zhou Huibo，Song Shenmin，Song Junhong，et al.Design of second-order sliding mode guidance law based on the non-homogeneous disturbance observer［J］.Journal of Control Science and Engineering，2014（2014）：1-10.

［11］Shtessel Y，Taleb M，Plestan F.A novel adaptivegain super-twisting sliding mode controller：Methodology and Application［J］.Automatica，2012，48（05）：759-769.

［12］Shtessel Y，Kochalummoottil J，Edwards C.Continuous adaptive finite reaching time control and secondorder sliding modes［J］.IMA Journal of Mathematical Control and Information，2013，30（01）：97-113.

［13］Levant A.Principles of 2-sliding mode design［J］.Automatica，2007，43（4）：576-586.

［14］Levant A.Higher-order sliding modes，diffierentiation and output-feedback control［J］.International Journal of Control，2003，76（9）：924-941.

［15］李雪冰，馬莉，丁世宏.一類新的二階滑模控制方法及其在倒立擺控制中的應(yīng)用［J］.自動化學(xué)報，2015，01（41）：193-202.

［16］袁贛南，左志丹，曲桂婷，等.二階滑模變結(jié)構(gòu)控制系統(tǒng)的滑模到達條件［J］.華中科技大學(xué)學(xué)報：自然科學(xué)版，2013，06（41）：70-75.

［17］楊永彬，趙賀偉，李涵.基于反演設(shè)計的無人水下航行器自適應(yīng)二階滑模控制［J］.海軍航空工程學(xué)院學(xué)報，2016，02（31）：152-158.

Ship Course Control Based on Second Order Sliding Mode Method

LIU Yong，BU Renxiang，SUN Daming
（Navigation College，Dalian Maritime University，Dalian 116026）

According to sliding mode control ideas，a control input is designed and a new adaptive second order control algorithm is proposed for second order course control system of underactuated ships with nonlinearity，and uncertain external disturbances.The stability of control system is proved by Lyapunov stability theory and numerical simulation is carried out to validate the reasonableness and validity.The algorithm avoid dimensional explosion and without uncertainty estimating and it can guarantee the convergence and stability of closed-loop control system.Numerical simulation results verify the controller who is proposed by this algorithm is insensitive to external disturbances and system perturbation and has the invariability and excellent robustness，and it can effectively solve the problem of chattering and divergent in the nonlinear course control system which has a good practice value in the future.

underactuated ship；ship course control；second order sliding mode

U664.82

A

1672-9870（2017）04-0069-04

2017-05-26

遼寧省自然基金項目（201602084）；中央高校基本科研業(yè)務(wù)費專項資金資助項目（3132016008）

劉勇（1985-），男，碩士，講師，E-mail：liuyong_dlmu@163.com