最小二乘法在鐵路振動信號預處理中的應用

於崇銘，任風云，劉少坤

（1.空軍勤務學院航空彈藥系，江蘇徐州221000；2.空軍駐624廠軍代室，黑龍江 哈爾濱 150000）

最小二乘法在鐵路振動信號預處理中的應用

於崇銘1，任風云1，劉少坤2

（1.空軍勤務學院航空彈藥系，江蘇徐州221000；2.空軍駐624廠軍代室，黑龍江 哈爾濱 150000）

鐵路垂向振動加速度信號可以由加速度傳感器測得，但由于外界的各種干擾，數據往往呈現出非光滑性的特點，并且偏離了真實的數值，給模型的建立、參數估計帶來誤差。所以，在進行系統分析之前，要對測得的信號數據進行預處理。介紹了最小二乘法，并在MATLAB軟件上以實際案例進行了算法驗證。結果表明，通過該方法處理后的信號質量有著較為顯著的改善。

鐵路；振動信號；預處理；最小二乘法；MATLAB

在分析貨物鐵路運輸振動特性的過程中，通過構建鐵路運輸振動力學方程后，如何準確獲取振動力學模型中的參數成為分析其振動特性的關鍵環節。由于隨機信號的積分在正常情況下計算，是不能收斂的，所以其本身的傅里葉變換是不存在的，也不可能像確定性信號，如正弦信號，方波信號那樣用數學表達式來準確地描述。所以本文采用在仿真測試時提出的方法，根據哈密頓體系下的方程編程計算響應，在保證響應達到穩定后進行傳遞率的計算，進而與試驗所得的振動傳遞率進行參數識別、優化。

為了得到振動傳遞率的試驗值，需要用加速度傳感器分別測得貨物的振動響應加速度和火車車廂底板的加速度信號。但是由于各種干擾和雜波信號的存在，使得實際測得的加速度信號常常偏離其真實數值。減少或消除采樣數據中的干擾成分，使加速度信號盡可能接近真實值，是本文的重點工作。

1 消除多項式趨勢項

將內置加速度傳感器的測振儀放在列車上，在列車運行過程中采集到的振動信號數據，由于放大器對溫度比較敏感，隨溫度變化容易產生零點漂移；列車內的工作環境相對比較惡劣，影響傳感器的感應性能；當振動頻率超過傳感器頻率范圍時（低于最低額定頻率或高于最高額定頻率），其低頻性能的不穩定性特質往往會使信號數據偏離基線，偏離基線隨時間變化的這一過程叫做被測信號的趨勢項。趨勢項會直接影響到所測得加速度信號的正確性，應盡量將其去除或減少[1]。去除諸如此類趨勢項的方法很多，比較常用的是多項式最小二乘法。

對火車振動信號采樣頻率保持不變，即時間間隔是相等的。現通過測試，得到某一振動信號的測量數據為{xk}（k=1，2，3，…n），把采樣時間間隔設定為△t=1，那么多項式函數為：

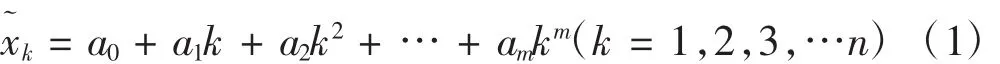
確定函數x~k的各個待定系數的值aj（j=0，1，…m），依據最小二乘法的定義，使得函數x~k與離散數據xk的誤差平方和達到最小值，即

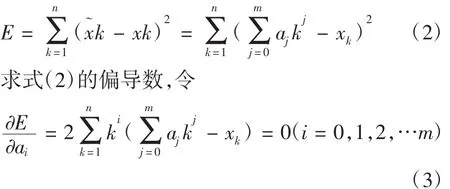
依次取E對參數a求偏導，可以得到一個m+1元的線性方程組：

解方程組（4），求出 m+1個待定系數的值aj（j=0，1，2，…m）.m上面各式中，是設定的多項式的階次大小，其值范圍為0≤j≤m.

當m=0時求得的趨勢項為常數，有

解方程，得

從式（6）中可以看出，當m=0時的趨勢項為被測信號的全部值的算術平均值。在此，需要消除常數趨勢項。其計算公式為

m≥2時為曲線的趨勢項，所以實際對采樣數據進行多項式趨勢項消除時，通常只要取m＝1～3，即可達到相關要求。

2 MATLAB程序實現

在了解計算原理后，需要相應平臺來進行實現。本文通過MATLAB軟件平臺來完成。之所以選用MATLAB，是因為其語言更為簡單、明了，尤其是在處理諸如上述相對復雜的計算過程和大量數據時，MATLAB的優勢更為明顯。

算法主要調用了MATLAB中polyfit和polyval這兩個主要函數。polyfit函數用來擬合最小二乘法給定階數的多項式，調用方式以先表示逼近，然后返回到指定項中。表達式 a=（t，x，m），表示在最小二乘法的基礎上，對輸入的數據t和x用m階多項式逐次進行逼近，結果返回一個長度為m+1的多項式系數，并將該系數存到向量a內；polyval函數是求多項式的值，調用方式b=polyval（a，t），表示用輸入變量t向量，計算系數向量a的多項式值，計算結果存到向量b中[2]。算法的核心部分如下：

clear

clc

close all hidden

fni=input

fid=fopen（fni，’r’）；

sf=fscanf（fid，’%d’，1）；

m=fscanf（fid，’%s’，1）；

fno=fscanf（fid，’%s’，1）；

x=fscanf（fid，’%f’，inf）；

status=fclose（fid）；

n=length（x）；

t=（0：1/sf：（n-1）/sf）；

a=polyfit（t，x，m）；

y=x-polyval（a，t）

subplot（2，1，1）；

plot（t，x）；

grid on；

subplot（2，1，2）；

plot（t，y）

gird on；

fid=fopen（fno，’w’）

for k=1；n

fprint（fid，’%f%f ’，t（k），y（k））；end

status=fclose（fid）；

3 算法驗證

通過以上方法，把實際測得的鐵路運輸振動信號剔除趨勢項后，就能準確計算出振動傳遞率的值，與傳遞率的理論值比較，進行參數識別后，就能給構建的鐵路運輸振動模型賦值。本文以50t車測得的振動數據為參考進行算法驗證[3]。從列車駛出車站，過岔道，運行過程中的車體搖動、顫動、鋼軌接縫處、過橋梁直至駛入車站的全過程[4]，主要考慮列車的垂向加速度。

輸入數據文件的內容如下：

250.0

7

out.txt

0.6 4.0 2.0 3.9 6.2 2.4 2.6

0.5 3.9 2.1 4.2 6.3 2.8 2.4

……

計算結果如圖1所示。

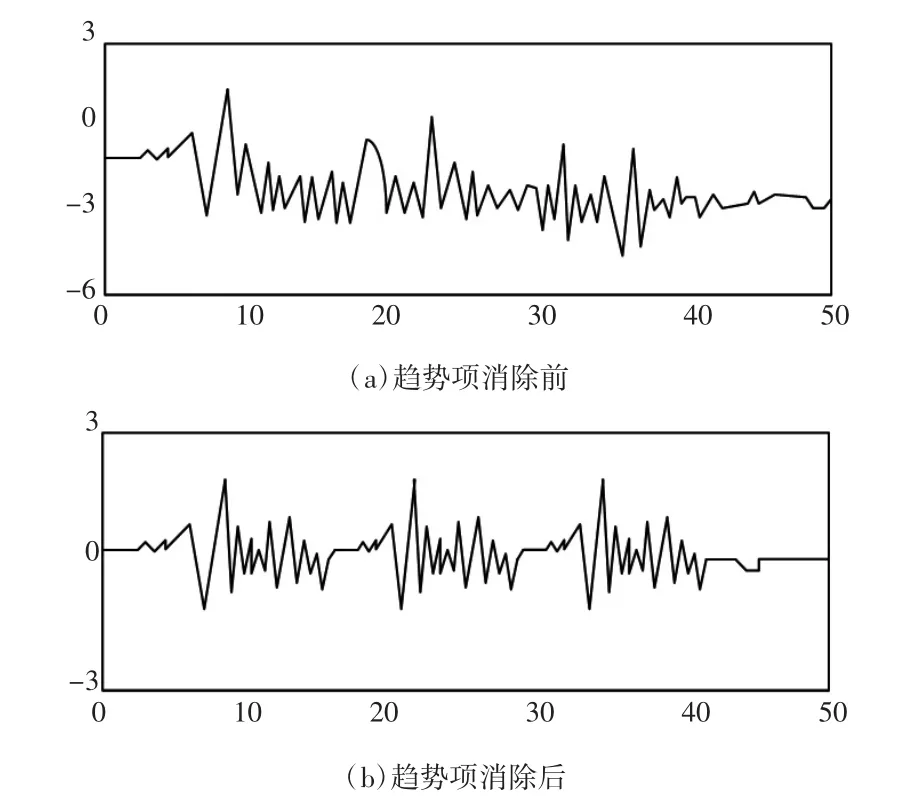
圖1 鐵路振動信號多項式趨勢項消除前后波形的對比

由圖可知，消除多項式趨勢項處理后的數據波形明顯得到了改善，更具有規律性和可參考性。可見，該方法在提高鐵路垂向振動信號的質量方面有明顯的效果。

4 結論

本文介紹了最小二乘法在振動信號預處理中的應用，通過消除多項式趨勢項，并在MATLAB軟件上以一定的算法程序編程實現。以50 t車實際測得的鐵路垂向振動加速度數據為例，對算法進行了驗證。該算法清晰明了，程序簡潔，計算量相對較小，便于模塊化管理。結果表明，利用該方法對鐵路垂向的振動信號進行預處理，可以較為顯著地提高振動信號的質量。

[1]王 濟，胡 曉.MATLAB在振動信號處理中的應用[M].北京：中國水利水電出版社，2006：69-70.

[2]李柏年，吳禮斌.MATLAB數據分析方法[M].北京：機械工業出版社，2012：3-7.

[3]段虎明，石 峰.路面不平度研究綜述[J]振動與沖擊，2009，28（9）：95-97.

[4]周勁松.鐵道車輛振動與控制[M].北京：中國鐵道出版社，2012：21.

The Least Square Method in the Application of Railway Vibration Signal Preprocessing

YU Chong-ming1，REN Feng-yun1，LIU Shao-kan2
（1.Department of Aviation Ammunition Air Force Logistics College，Xuzhou Jiangsu 221000，China；2.The Military Representative Office of Air Force in 624 Factory，Harbin Heilongjiang 150000，China）

Through the acceleration sensor acquisition to the vibration acceleration of railway signal often present a non-smooth characteristics due to interference，and deviates from the true value，bringing error for the establishment of the model and parameter estimation.Therefore，the preprocessing of vibration signal is very important.The paper discuss the eliminating method of polynomial trend term on MATLAB software platform for the algorithm validation.The results show that the processed signal quality has been improved obviously.

railway；vibration signal；preprocessing；the least square method；MATLAB

U284

A

1672-545X（2017）08-0136-03

2017-05-10

於崇銘（1992－），男，江蘇南通人，碩士研究生，研究方向：鐵路運輸振動特性研究。