小學數學教學中數形結合的運用

程小愛

（永修縣新城小學，江西九江 330304）

小學數學教學中數形結合的運用

程小愛

（永修縣新城小學，江西九江 330304）

數學是研究客觀世界的數量關系和空間形式的科學。同一個客觀事物所具有的數和形的屬性相互聯系，又在一定的條件下相互轉化。利用這種轉化，使數形結合，有利于數學問題化難為易。數形結合的方法在小學數學教學中有廣泛的應用。做到數形結合能啟迪學生的思維，有效提高學生解決問題的能力。

小學數學；數形結合

一、運用數形結合揭示概念本質

概念是人們反映事物本質屬性的思維形式，正確理解概念和運用概念是提高學生思維能力的基礎。學生學習概念的過程是一個復雜的思維過程，教學中教師應注重在感性認識的基礎上，采用數形結合，通過比較、分析和綜合，抽取概念的本質，從而全面明確概念，掌握概念的本質特征。

案例1：《倍的認識》教學片斷（多層練習完善“倍”的認識）

1.擺圓片

現在，請孩子們拿出6個圓片，擺成上下2行，使兩行的圓片數量成倍數關系。請輕輕地拿出學具擺一擺。

交流：第一行擺幾個，第二行擺了幾個幾，誰是誰的幾倍？

2.拍手游戲

孩子們，你們剛才的表現可真棒！老師也忍不住要為你們鼓掌。（老師拍3下）提問：誰聽清楚了，剛才老師拍了幾下？誰能拍出老師的2倍？要讓大家清晰地聽出2倍的關系，注意停頓。提問：老師拍了3下，你拍了幾個幾下？他拍對了嗎？孩子們，你們會拍了嗎？聽好了（老師拍2下）請拍出我的3倍。（老師拍4下）請拍出我的2倍。誰來當小老師拍一拍？

3.創造一幅“2倍”關系圖

孩子們，接下來我們來進行一個小小設計師的比拼，請各位小設計師們發揮想象，創造一幅2倍關系圖，注意要求：一個數量是另一個數量的2倍。請拿出紙和筆畫一畫，看誰創造的圖既準確又美觀。學生畫完后投影展示學生作品。提問：你畫了什么？誰是誰的幾倍？

剛才大家創造出了這么多2倍關系的圖，真棒！能不能用一個圖表示所有的2倍關系呢？先4人小組討論一下，再動手畫一畫。

生：

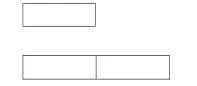
師：數學家們經常用線段圖來表示數量之間的關系。（邊講邊出示線段圖）用這一條線段表示一份數，2段這么長的線段就表示它的2倍。

思考：

首先通過擺一擺、拍一拍等活動，讓學生逐漸從感性認識開始向理性理解過渡，進一步鞏固倍的認識。

接著讓學生創造2倍關系圖，再從中抽象、概括，用一個圖表示所有的2倍關系，逐步逼近線段圖。在多樣的情境中，不同形態的非本質屬性方面的變化，需要孩子去捕捉其中不變的本質因素。在這樣的思維活動體驗中，獲得的概念就更精確、更穩定。

二、運用數形結合分析數量關系

解決問題的關鍵是幫助學生理解和分析數量關系，采用數形結合的方法，把抽象的數量關系正確、直觀地表現出來，可以更好地吸引學生的注意力，同時可以培養學生的觀察能力，增強學生思維的深刻性，從而提高學生的解題能力。

案例2：《連乘問題》教學片斷

1.課件出示教材第52頁例3超市銷售保溫壺情境圖。

2.提問：你們從剛才的圖片中收集到了哪些數學信息？數學問題是什么？同桌交流，指名匯報。

3.要求：一共賣了多少錢？你會先求什么，再求什么？

小組合作交流：

①拿出課前準備好的紙盒和保溫壺圖片，擺一擺，看一看，說一說。②嘗試畫線段圖分析數量關系。

思考：1.通過小組合作交流，借助保溫壺、紙箱等實物圖片，幫助學生直觀理解，讓學生的思維變成看得見、摸得著的東西。

2.嘗試畫線段圖分析理解，既體現了教法與學法的多樣性，又體現了數形結合的模式。線段圖能形象、直觀地反映應用題的數量關系，是應用題中實際事物數量方面的“表象”，它能起到化隱為顯，使數量關系明朗化的作用，有利于尋求解題思路，它是直觀與抽象的對立統一體。

三、運用數形結合拓展思維能力

數學是鍛煉思維的體操，數學的教學目的就是要培養數學思維能力，在小學主要培養學生初步的邏輯思維、形象思維和直覺思維能力。數形結合的思想能夠變抽象思維為形象思維，有助于把握數學問題的本質。

案例3：《數與形》教學片斷（1）

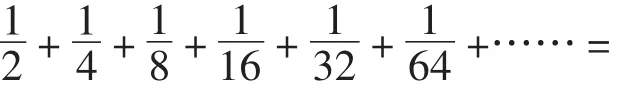
師：觀察這個算式，它有什么特點？

師：算式最后的省略號是什么意思？

生：后面還有很多數，有無數個。

師：無數個就是數也數不完，按照這樣的規律無盡地加下去，結果會等于多少呢？（讓同學們猜一猜）

師：沒感覺是嗎？不著急，我們剛剛說了，數可以幫形，其實形也可以助數。同學們，你們可以利用圖形幫助自己找找感覺。

請學生拿出練習紙（提示：把自己拿到的圖形看作單位“1”）

師：請你用你練習紙上的圖形來幫助自己，看看能不能找到和是多少。四人一小組展開討論。要求學生一定要涂一涂，畫一畫，組長操作，其他同學參考。

交流：出示三種不同的圖形作品，讓學生感受最后的結果。（結合算式講解）

1.圓形 2.正方形 3.線段

讓孩子介紹，自己畫的過程，讓學生感受最后的結果。

師：聽完了他們的介紹，你認為按這樣的規律加下去，算式的結果會是多少呢？

生：有的孩子可能認為等于1，有的孩子可能認為無限接近1。

師：雖然同學們得出的結果不相同，但是我看出結果也有共同的地方，都和誰有關？

生：都和1有關系。

師：無論是覺得等于1，還是覺得和1差一點，起碼我們有了一個方向。是誰幫助我們找到了方向呢？

生：圖形。

師：對，這就是圖形的好處，它能給我們感覺，讓我們找到接近結果的方向。但是我們還有困惑，結果到底是怎樣的呢？你們覺得圖能回答這個問題嗎？

生：不能。

師：這就是圖的缺陷，它不能準確、精細地表示結果。但是我們可以借助數來對它進行驗證，請同學們看一看。出示逆向思考的過程。

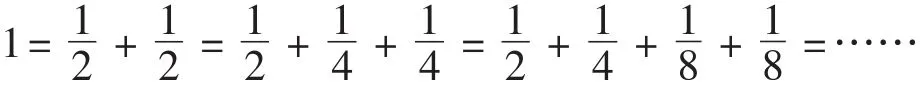
通過上面的題目，你覺得數和形有關系嗎？

師：是的，數與形的關系密切，你來幫我，我來助你。

《數與形》教學片斷（2）

為什么a×b+a×c=a×（b+c）？請畫圖解釋。

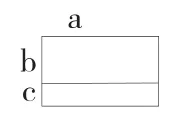
思考：

數與形的例題及乘法分配律的反運用都是學生認知上的一個障礙，有時很難用語言來描述，如果結合圖形來幫助學生理解，通過圖形變“無形”為“有形”，借助圖形完成轉化，對學生來說，收獲的不僅僅是知識方法，還經歷了一次發現、體驗和創造的過程，對數和形的結合會有更深刻的體會和感悟。

四、運用數形結合提高解題能力

數形結合思想是一種可使復雜問題簡單化、抽象問題具體化的數學思想方法。巧妙運用數形結合的思想方法解決一些抽象的數學問題，可起到事半功倍的效果。

例如：甲、乙兩車都從A地到B地，甲車比乙車提前30分鐘出發，行到全程時，甲車發生了故障，修車花了15分鐘，結果比乙車晚到B地15千米，甲車修車前后速度不變，全程為300千米，那么，乙車追上甲車時距A地多少千米？

思考：行程應用題對于小學生來說本身就是一個難點，信息一多更是不知從何下手，用方程來解答也有一定難度。可如果用數形結合的方法來解答就容易多了，畫圖如下：

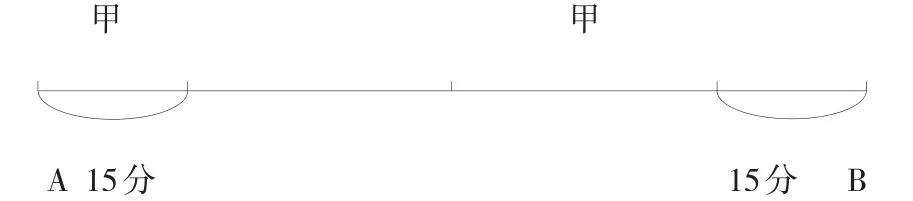
從圖中我們不難發現，乙車追上甲車時距A地300÷2＝150（千米），因為甲車提前了15分鐘（提前30分鐘減去修車的15分鐘），又晚到15分鐘，根據圖形的對稱性，就知乙車在中點追上甲車，這樣問題就迎刃而解了。

總之，看“形”思“數”，見“數”想“形”，通過數形結合，實現轉化，不僅能豐富分析和解決問題的策略，更有助于透徹地理解數學關系的本質，提升學生的數學素養。

程小愛（1968—），男，江西永修人，永修縣新城小學，高級教師，研究方向為小學數學教學。

責任編輯徐艷蘭