培養學生數學核心素養的研究與實踐

方兆繼

（廣德縣教學研究室，安徽宣城 242200）

培養學生數學核心素養的研究與實踐

方兆繼

（廣德縣教學研究室，安徽宣城 242200）

數學思想方法是在啟發學生數學思考的過程中逐步積累和形成的，它不是一朝一夕就能立竿見影，必定要經歷一個循環反復、螺旋上升的過程。因此在教學中，教師要重視數學思想的教學，根據學生認知規律、年齡特征，挖掘蘊含在教材顯隱性資源，創造并把握運用數學思想解決問題的機會，主動培養學生運用數學思想的意識，使學生從數學思想方法的高度把握知識的本質和內在規律，逐步體會數學思想方法的精神實質，從而使數學素養全面提高。

數學素養；課堂教學；數學本質

核心素養是學生數學素養的重要標志。數學素養是通過數學的學習建立起來的一些思想、方法，以及用數學的思想方法處理和解決問題的能力。數學核心素養是基于認數、計算、測量、統計等具體的數學知識與技能而形成的思想與方法，以及對數學在現實社會與生活中的作用與價值的認識。

一、深入挖掘教材，培養數學核心素養

數學核心素養一般與學習領域內容相關。如，數感、符號意識、運算能力與“數與代數”領域直接相關，在學習數的認識、數的運算、運用字母表示數等內容時，與這些核心素養直接聯系，數的認識學習過程有利于形成學生的數感，建立數感有助于學生數的理解和把握。數學知識在內容上貫穿兩條主線，一是數學基礎知識，是一條“明線”，它直接以文字形式寫在教材里；二是數學思想，是一條“暗線”，隱藏在基礎知識的背后，是無“形”的，需要教師通過對教材加以分析挖掘，撥云去霧，才能顯露出來。新教材注重貫徹四基目標，低年級教材知識看似簡單，但也蘊含了豐富的數學思想，各種思想聯系緊密，互相滲透，一個數學內容往往是幾種思想方法交織在一起。

以一年級上冊“比多少”教材為例：

圖1 情境圖

圖2 比多少

教材中小猴和各類水果是散亂放在一起的，教學時要先進行分類（分類思想）；統計出數量（統計思想），再根據數量多少來比較數的大小（一一對應思想），并引出符號＞、＜、=（符號思想）。簡單的一課中蘊含著豐富的隱性數學思想，這就需要教師挖掘提煉，有意識地從教學目標的確定、教學過程的預設、教學效果的落實等方面來滲透數學思想，從而發展學生數學素養。

抽象思想是重要的數學基本思想之一，存在于數學學習的全過程。低年級教材主要是讓學生能從具體情境中抽象出數量和變化規律，并用符號表示，符號化的過程就是一個抽象的過程。從情境圖抽象出數字符號0～9，關系符號=、＜ ＞，運算符號+ 、－、×、÷都是典型的符號化。在數的教學中，可根據教學的實際情況，適當地展示數字的形成過程和所運用的思想，讓學生體驗符號思想的簡明，培養學生的創造性思維。

二、注重過程，培養學生核心素養

為了更好地培養學生的數學思維品質，教師不僅要對教材進行研究，潛心挖掘，還要講究數學思想滲透的手段和方法，回歸和再現知識的形成過程，讓學生在探究過程中自主發現潛藏其中的思想方法，體驗數學思想魅力，從而提高數學素養，這才是數學教學應有的視界。

小學數學中有相當的比重是計算，教學中要引導學生在觀察、比較、抽象、概括中理解算理，掌握方法。數形結合是理解算理的很好的方式。如一年級下冊“兩位數加一位數和整十數”，教學25+2和25+20時，教師先請學生擺小棒，在對比中學生明白：2要和25中的5相加，它們的計數單位都是1；20要和25中十位上的2相加，它們的計數單位都是十。這樣，通過擺小棒，有效滲透數形結合思想，使復雜問題簡單化，抽象問題具體化，相同數位相加的算理簡明直觀，學生在理解算理的基礎上掌握計算方法，發展數學思維。

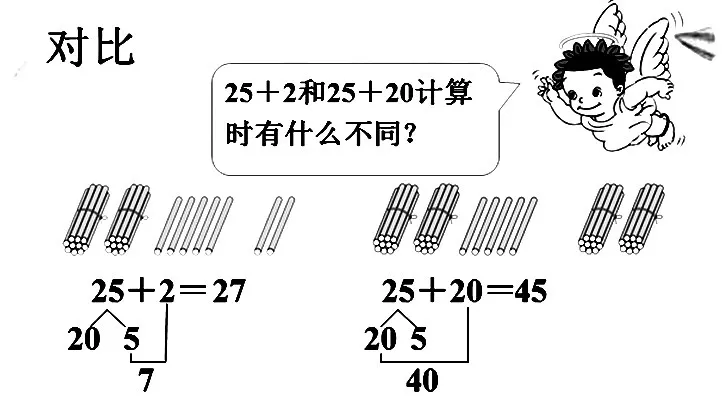
圖3 兩位數加一位數、整十數

又如在量的教學中，首要問題是要合理引入計量單位。在“面積與面積單位”的教學中，教師可以這樣設計：當觀察、重疊都無法直接比較兩個圖形面積的大小時，引入小方塊，并把它一個個鋪在兩個圖形上，這樣，使兩個圖形的面積得到量化，使形的問題轉化為數的問題；接著又出示大小不一的方塊進行測量，得到與觀察結果不符的數，進而使學生意識到，任何量的量化都必須有一個統一的標準，這樣自然引入計量單位。

圖4 用小正方形進行測量

圖5 小正方形大小要有統一標準

數學在本質上就是在不斷的抽象、概括、模式化的過程中發展和豐富起來的。數學學習只有深入到模型的意義上，才是一種真正的數學學習。低年級學生以形象直觀思維為主，需要由具體、形象的實例開始，借助操作予以內化和強化，最后通過思維發散和聯想加以擴展和推廣。

數學思想方法滲透是無形的，是無法傳授的，只有讓學生一次次經歷、體驗后才能感悟。教學中要有意識地引導學生經歷知識的形成過程，讓學生在自主探究時、在合作交流中不僅學到數學知識，還發現知識背后蘊含的數學思想，得到積極的情感體驗，培養學生核心素養。

三、學以致用，培養學生核心素養

數學思想方法的教學，不僅是為了指導學生有效應用知識，更是培養學生的思維品質。教學中要加強學生的應用意識，鼓勵學生運用已學的數學思想方法去發現、分析問題，引導學生加以抽象、概括，建立數學模型，探求解決問題的一般方法，培養學生自覺的應用意識，進而積累數學思想，培養學生核心素養。

如：在教學三年級《數學廣角——排列組合》一課中，在解決“2件上裝和3件下裝一共有幾種不同的搭配方法？”時，借助圖形連線，學生觀察到：下裝有3件時，一件上衣就有3種搭配，2件上衣就有2×3種搭配方案；下裝是4件時，2件上衣就有2×4種搭配方案。

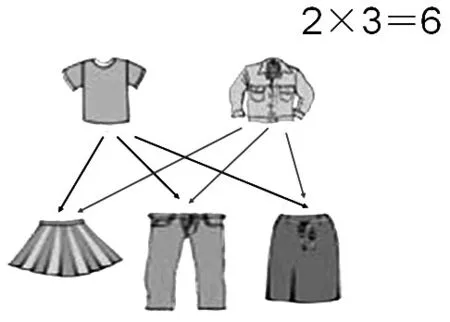
圖6

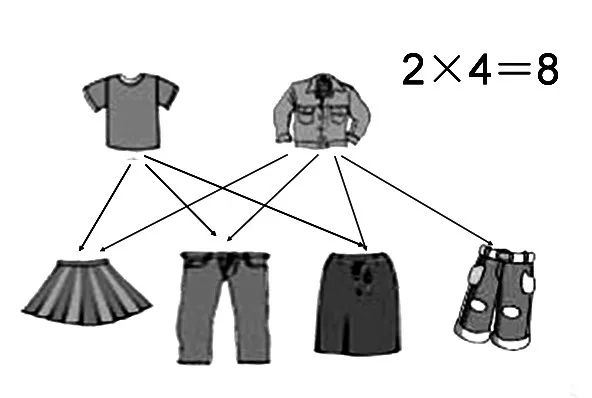
圖7

這樣由具體、形象的實例開始，借助操作予以抽象概括，通過形—數—算的數學思想的層層遞進，建立模型，學生就可以脫離實物圖舉一反三，通過思維發散和聯想加以擴展和推廣，解決早餐問題、路線問題，滲透數學建模思想，學生的數學素養得到提升。

教材編寫中將一些重要的數學概念與數學思想方法的內容，采用螺旋上升的方式。教師在使用時，要加深對教材的理解和挖掘，采用逐步深化的方式，潛移默化地融數學思想方法于知識教學、技能培養之中，以便逐步實現每一個階段的滲透目標，同時還要注意各種思想方法間的承接關系，做到每個階段都有所提升、有所拓展，切實提高學生的數學素養。

這樣，抓住知識間的聯系，借助于直觀圖示的形象支撐，讓學生充分展開探索過程，建立起一位小數的“直觀模型”。接著借助長度單位這個背景，讓學生自主拓展到百分之幾的分數用兩位小數表示，實現知識的正遷移，這種形象的直觀模型對后面學習三位小數以及抽象概括小數的意義無疑具有統攝作用。在滲透思想方法的時候，教師引導學生自覺地運用學到的思想方法去遷移拓展，提高學生自覺的應用意識，積累數學思想。

數學思想方法是在啟發學生數學思考的過程中逐步積累和形成的，它不是一朝一夕就能立竿見影，必定要經歷一個循環反復、螺旋上升的過程。因此在教學中，教師要重視數學思想的教學，根據學生認知規律、年齡特征，挖掘蘊含在教材中的隱性資源，創造并把握運用數學思想解決問題的機會，主動培養學生運用數學思想的意識，使學生從數學思想方法的高度把握知識的本質和內在規律，逐步體會數學思想方法的精神實質，從而使數學素養全面提高。

方兆繼（1977—），男，安徽廣德人，廣德縣教學研究室，小學高級教師，研究方向為小學數學教學。

責任編輯徐艷蘭