時滯擾動類Lorenz系統的Hopf分岔

李文娟, 牛瀟萌, 李旭超, 俞元洪

(1.赤峰學院數學與統計學院,內蒙古 赤峰 024000;2.赤峰學院計算機與信息工程學院,內蒙古 赤峰 024000);

時滯擾動類Lorenz系統的Hopf分岔

李文娟1, 牛瀟萌1, 李旭超2, 俞元洪2

(1.赤峰學院數學與統計學院,內蒙古 赤峰 024000;2.赤峰學院計算機與信息工程學院,內蒙古 赤峰 024000);

通過非線性動力學理論,對時滯類 Lorenz系統在平衡點的穩定性問題和發生Hopf分岔的條件進行了研究.首先計算得到系統的平衡點,然后通過分析系統在平衡點處的相應特征方程根的分布,得到系統在平衡點局部漸近穩定和產生Hopf分岔的時滯臨界點.以時滯為分叉參數,研究了時滯系統存在Hopf分岔的條件.最后,利用Matlab程序進行仿真驗證所得結論與理論分析一致.本文的結論是對一些已有文獻研究成果的推廣.

時滯;類Lorenz系統;穩定性;Hopf分岔

1 引言

自1963年,美國氣象學家Lorenz在研究區域小氣候時提出了第一個經典的Lorenz系統[1]以來,混沌系統得到了更廣泛的研究和應用.此系統在混沌學歷史上有著重要的地位,特別是對它的分析在了解非線性方程如何出現混沌解方面很有意義.隨著對Lorenz系統研究的不斷深入,各種新的類Lorenz混沌系統大量產生,這種新的類Lorenz混沌系統在保密通信、激光物理、控制工程、化學反應和生物醫學等領域應用廣泛[2-4].現有的各種新的類Lorenz混沌系統仍無法滿足各領域應用的需要,于是人們開始尋找新的類Lorenz混沌系統,在此期間,很多學者得到一些行為復雜的系統,例如Chen系統、Lu系統、Liu系統、Qi系統、Chua系統等[5-9].但是上述研究主要是混沌的同步和控制,對分岔的研究相對較少.對于時滯類Lorenz系統的研究更是不多.

2015年,文獻[10]提出了一類新的類Lorenz系統

其中x,y,z是狀態變量，a,b,c,d為系統參數．2015年,文獻[11]提出了一類帶時滯的類Lorenz系統

其中x,y,z是狀態變量;a,b,c,d為系統參數;τ＞0為系統常量時滯．

本文的主要結果是將文獻[11]的系統(2)中第一個非線性方程中的a(y?x)改為

第二個非線性方程中的bx(t?τ)改為bx,第三個非線性方程中的dx2改為

得到一類新的雙時滯類Lorenz系統.通過對一類新的雙時滯類Lorenz系統在零平衡點的線性化系統的特征方程的分析給出該系統在零平衡點的穩定性問題和發生Hopf分岔的條件.最后通過數值擬真驗證所得結論的正確性.本文研究的是雙時滯類Lorenz系統,文獻[10]研究的是沒有時滯的類Lorenz系統,文獻[11]研究的是單時滯的類Lorenz系統.當本文中的時滯為零時即為文獻[10]研究的系統.

2 主要結果及證明

本文考慮時滯類Lorenz系統:

其中x,y,z是狀態變量;a,b,c,d,h為系統參數;τ＞0為系統常量時滯,可理解為信號傳輸的阻礙時間等.設系統參數

系統(3)的平衡點滿足下列條件:

由(4)式知系統(3)的平衡點有三個,它們分別為

2.1 平衡點穩定性分析

定理 2.1假設τ=0,則系統(3)在平衡點

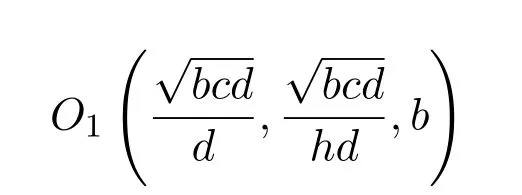
處是不穩定的.

證明在平衡點

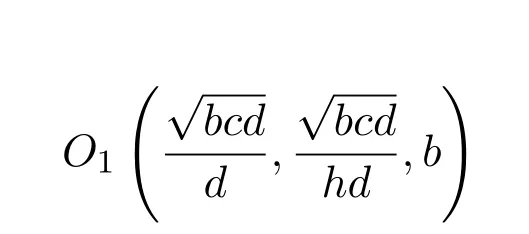
處,系統(3)的Jacobian矩陣為:

矩陣(5)對應的特征方程為:

即

其中

當τ=0時,(6)式轉化為

因為系統參數 a＞0,b＜0,c＞0,d＞0,h＞0,所以 2abch＜0根據羅斯 -霍維茲(Routh-Hurwitz)判據可知,(7)式的特征根具有正實部.所以當τ=0時,系統(3)在平衡點

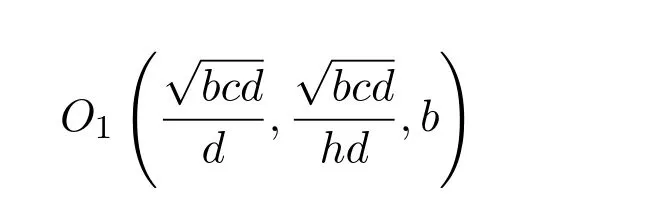
處是不穩定的.

注 2.1因為在變換S:(x,y,z)?→(?x,?y,z)的作用下具有不變性,即關于z具有對稱性.所以只討論系統(3)在平衡點

的穩定性.

下面討論在平衡點O(0,0,0)處的穩定性.在平衡點O(0,0,0)處易求得線性化系統

線性化系統(8)對應的特征方程為

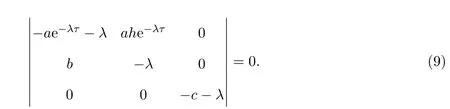
特征方程(9)可化為

其中

引理 2.1假設τ=0,則系統(3)在平衡點O(0,0,0)處是漸近穩定的.

證明當τ=0時,(10)式轉化為

因為系統參數a＞0,b＜0,c＞0,d＞0,h＞0,所以(a+c)＞0,?abch＞0且有

根據羅斯 -霍維茲 (Routh-Hurwitz)判據可知,(11)式的所有特征根都具有負實部.所以當τ=0時,系統(3)在平衡點O(0,0,0)處是局部漸近穩定的.

2.2 Hopf分岔問題

接下來討論在平衡點O(0,0,0)處的Hopf分岔存在的條件.

當τ＞0時,由于只考慮虛根,方程(10)等價于下面方程

設λ=iω(ω是大于零的常數）是(10)式的一個純虛根,則虛部ω滿足

根據復數相等可得

由三角函數的等式推得(13)式可化為

對(14)式有以下結論.

引理 2.2(14)式至少有一個正實根.

證明令u=ω2,則式(14)可化為

設

由(16)式得

根據函數零點存在定理,至少存在一個實數u0∈(0,+∞),使得f(uo)=0.所以(15)式至少有一個正實根．因為u=ω2,從而(14)式至少有一個正實根.

設ω0為(14)式的正實根,則(10)式有一純虛根iω0.又由(13)式得

將ω=ω0代入方程(17),則時滯τ的值為

因此 (iω0,τk)是 (10)式的解,即當時滯 τ=τk時,λ=±iω0是 (10)式的一對共軛的純虛根.

設τ0=min{τk},則時滯τ=τ0是(10)式出現純虛根λ=±iω0時τ的最小值.故可得如下的引理3.

引理2.3如果

那么(10)式有一對純虛根

設(10)式的特征根

滿足

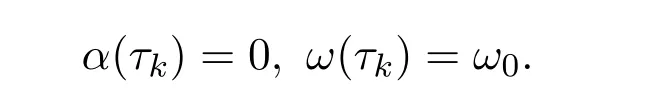
引理 2.4對于任意的τ=τk/=0,則

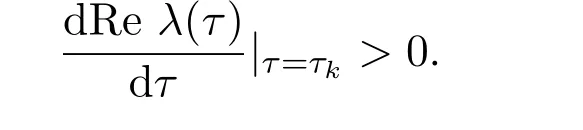
證明對(10)式兩邊關于τ求導，可得

由(10)式可得

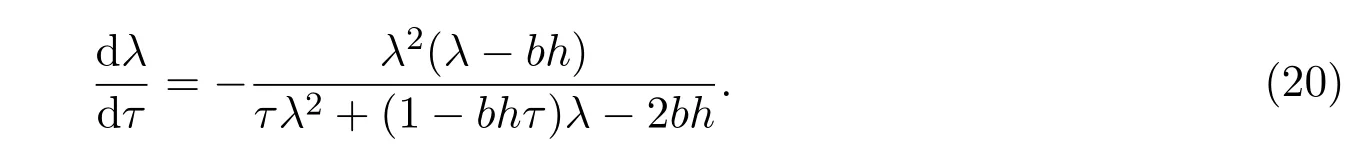
易得

由(21)式和

可得

由于

同號.證畢.

根據引理2.1-引理2.4和Hopf分岔理論可得下面結論．

定理2.2如果

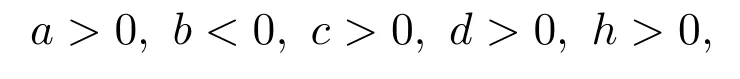
那么

(1)當τ∈[0,τ0)時,系統(3)在平衡點O(0,0,0)是漸近穩定的;

(2)當τ＞τ0時,系統(3)在平衡點O(0,0,0)是不穩定的;

(3)當

時,系統(3)在平衡點O(0,0,0)處發生Hopf分岔,產生極限環.

注 2.2定理的結論可以由下部分的數值仿真來驗證.文獻[1]的系統是系統(3)中

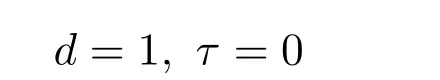
時的特例.此外,定理也推廣了文獻[2]的結果.

3 數值仿真

時滯類Lorenz系統(3)的參數a＞0,b＜0,c＞0,d＞0,令

這時系統(3)可化為

利用Matlab軟件計算得(11)式的正實根

和(15)式中

故,由定理可得下面的推論.

推論3.1如果

則

(1)當τ∈[0,0.7111)時,系統(23)在平衡點O(0,0,0)是漸近穩定的;

(2)當τ＞0.7111時,系統(23)在平衡點O(0,0,0)是不穩定的;

(3)當

時,系統(23)在平衡點O(0,0,0)處發生Hopf分岔,產生極限環.

下面用Matlab軟件繪出時滯τ取不同值時,系統(23)的狀態變量隨時間t的軌線圖和相圖,驗證所得結論的正確性.

圖1-1 時滯τ=0.7時,系統(23)的狀態 變量x隨時間t的軌線圖

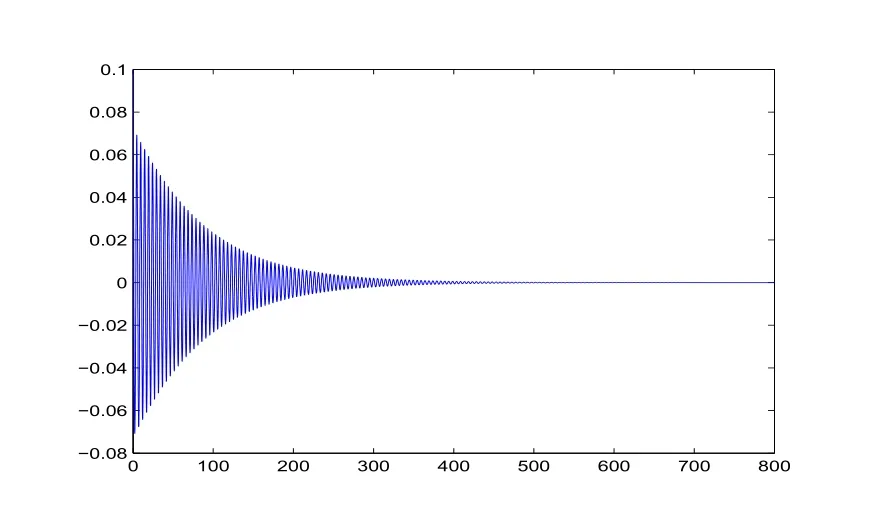
圖1-2 時滯τ=0.7時,系統(23)的狀態 變量y隨時間t的軌線圖

圖1-3 時滯τ=0.7時,系統(23)的狀態 變量z隨時間t的軌線圖

圖1-4 滯τ=0.7時,系統(23)的狀態 在xoy平面內的相圖

從圖 1-1、圖1-2、圖1-3可以看出，當時滯τ=0.7時,系統(23)的狀態變量x,y,z的值隨時間t的增大而趨于平衡點O(0,0,0),所以系統(23)在平衡點O(0,0,0)是漸近穩定的．

圖2-1 時滯τ=0.7111時,系統(23)的狀態變量x隨時間t的軌線圖

圖2-2 時滯τ=0.7111時,系統(23)的狀態 變量y隨時間t的軌線圖

圖2-3 時滯τ=0.7111時,系統(23)的狀態}變量z隨時間t的軌線圖

圖2-4 時滯τ=0.7111時,系統(23)的狀態 在xoy平面內的相圖

從圖2-1、圖 2-2、圖 2-3可以看出,當時滯 τ=0.7111時,系統(23)的狀態變量 x,y,z的值隨時間t的增大保持等周期震蕩,所以系統(23)在平衡點O(0,0,0)處發生Hopf分岔,產生極限環.

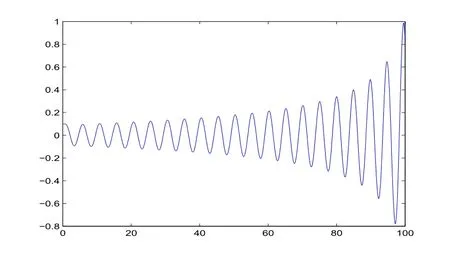
圖3-1 時滯 τ=0.72時,系統(23)的狀態變量x隨時間t的軌線圖

圖3-2 時滯τ=0.72時,系統(23)的狀態 變量y隨時間t的軌線圖

圖3-3 時滯 τ=0.72時,系統(23)的狀態 變量z隨時間t的軌線圖

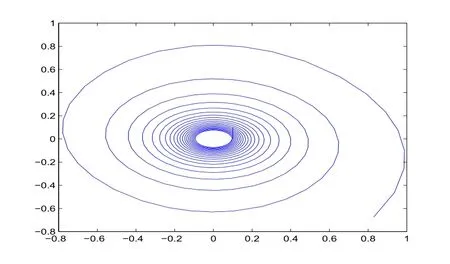
圖3-4 時滯τ=0.72時,系統(23)在xoy平面里的相圖

從圖3-1、圖3-2、圖3-3可以看出,當時滯τ=0.72時,系統(23)的狀態變量x,y,z的值隨時間t的增大而逐漸遠離平衡點O(0,0,0),說明系統(23)在平衡點O(0,0,0)是不穩定的.

圖 1-4、圖 2-4、圖 3-4可以看出,當時滯 τ＜τ0,τ=τ0,τ＞τ0時,系統 (23)xoy平面內的相圖.

[1]Lorenz E N.Deterministic non-periodic fl ows[J].J.Atmos.Sci.,1963,20:130-141.

[2]劉式適,劉式達.物理學中的非線性方程[M].北京:北京大學出版社,2012:341-345.

[3]王興元.混沌系統的同步及在保密通訊中的應用[M].北京:科學出版社,2012:356-385.

[4]劉揚正.超混沌Lü系統的電路實現[J].物理學報,2008,57(3):1439-1443.

[5]Wenxin Q,Gangrong C.On the boundedness of solutions of the Chen system[J].J.Math.Anal.Appl.,2007,329(1):445-451.

[6]Mkaouar H,Boubaker O.Chaos synchronization for master slave piecewise linear systems application to Chua’s circuit[J].Commun Nonlinear Sci.Numer Simulat.,2012,17(3):1292-1302.

[7]Chongxin L,Tao L,Ling L,et al.A new chaotic attractor[J].Chaos,Solitons and Fractals,2004,22:1031-1038.

[8]Yongguang Y,Suochun Z.Hopf bifurcation in the Lü system[J].Chaos,Solitons and Fractals,2003,17(5):901-906.

[9]Guoyuan Q,Gangrong C,Shengzhi D,et al.Analysis of a new chaotic system[J].Physica A,2005,352:295-308.

[10]官國榮,吳成茂,賈倩.一種改進的高性能Lorenz系統構造及其應用[J].物理學報,2015,64(2):1-14.

[11]李德奎,連玉平.單時滯類Lorenz系統的Hopf分岔分析[J].數學雜志,2015,35(3):633-642.

Hopf bifurcation analysis of the disturbed Lorenz-like System with the delayed

Li Wenjuan1,Niu Xiaomeng1,Li Xvchao2,Yu Yuanhong3
(1.School of Mathematics and Statistics,Chifeng University,Chifeng 024000,China;2.Computer and Information Technology Institute,Chifeng University,Chifeng 024000,China;3.Academy of Mathematics System Sciences,Chinese Academy of Sciences,Beijing 100190,China)

In this paper,we analyze the stability and Hopf bifurcation condition of the system at its balance by using the nonlinear dynamics theory.The equilibrium point is obtained and then critical point of the delay for local stability of the equilibrium and existence of local Hopf bifurcation is also obtained by analyzing distribution of roots of the corresponding characteristic equation.the condition for the existence of Hopf bifurcation of this delay system is studied by taking delay as bifurcation parameter.Furthermore,by Matlab program some numerical simulations were given to show the correctness of the obtained conclusion.This paper extends the research achievements in the cited literature.

time-delay,Lorenz-like system,stability,Hopf bifurcation

O175

A

1008-5513(2017)05-0475-11

10.3969/j.issn.1008-5513.2017.05.005

2017-03-27.

國家自然科學基金(11561001);內蒙古自然科學基金(2014MS0101);內蒙古高等學校科研基金（NJZY17301).

李文娟(1981-),碩士,講師,研究方向：穩定性理論及應用.

2010 MSC:34C10,34C15