關于Schrder路徑計數的幾個遞推式的組合證明

尹鵬君

(北京工商大學理學院,北京 100048)

尹鵬君

(北京工商大學理學院,北京 100048)

利用 Schrder路徑中不同類型的步的特點,研究不同初始高度的 Schr?der路徑,給出了Schrder路徑計數的遞推公式的組合證明.

Schrder 路徑;小 Schrder 路徑;初始高度

1 引言

Schr?der[1]曾提出用括號劃分一系列不同的字母的計數問題,并且給出了小Schr?der數的生成函數σ(x),

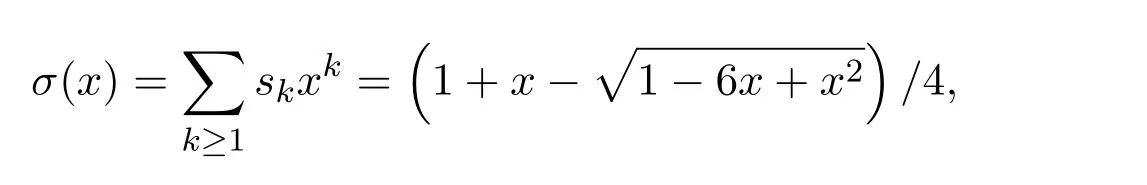
且滿足

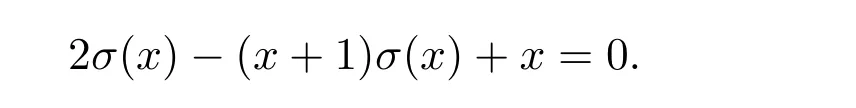
Shapiro和Sulanke[2]將(n+1)-多凸邊形轉化為平面樹,并將平面樹雙著色,再構造平面樹與 Schr?der路徑之間的雙射,從而證明了大 Schrder數是小 Schrder數的兩倍.Deutsch[3]將有序樹分成兩類,即矮灌木和高灌木,并利用這兩種有序樹在計數上相等且數量均為小 Schrder數的特性,給出了有序樹與 Schrder路徑的一一對應關系,進而巧妙、簡練地得出了大 Schrder數與小 Schrder數的兩倍關系.Huh和 Park[4]構造了長度為 n且可五著色的 Dyck路徑與推廣的 Schrder路徑的雙射,從而得出了推廣的 Schr?der路徑的計數公式.Yan[5]構造了長度為 2n的 Schrder路徑與 (2,3)-Motzkin路徑之間的雙射,給出了在限制不同類型步的條件下的 Schr?der路徑的計數公式.Song[6]定義了 m-Schr?der路徑,并給出了 m-Schr?der路徑的計數結果及證明.Chen和 Zhao[7]在 Shapiro和 Wang[8]的基礎上,構造了長度為n的k-Motzkin路徑與長度為 2n+2且不存在高度是偶數的水平步的 (k?2)-Schr?der路徑之間的雙射.另外,Schr?der數有很多組合結構.例如,長度為 2n且對每個峰進行二染色的Dyck路徑的計數[3]、劃分長度為(n+1)-多凸邊形的計數[2]等.同樣地,小Schr?der數也存在很多對應的組合結構.例如,有n+1個葉子且不含有節點出度為1的有序樹的計數[3]、劃分長度為(n+2)-多凸邊形的計數[3]及用括號劃分n+1個不同字母的種類數[1]等等.本文主要從組合意義的角度,證明關于Schr?der數的幾個等式[9].首先,介紹一些定義.

定義1.1一條長度為 2n的 Schr?der路徑是由上升 U=(1,1)、下降 D=(1,-1)和水平H=(2,0)構成、起于點(0,0)止于點(2n,0)且只存在于x軸上或者x軸上方的路徑.

定義1.2若路徑中任意一步的兩個端點的縱坐標中較大者為k,則稱該步的高度為k.特別地,x軸上的水平步的高度為0.

定義1.3給定一條路徑,如果這條路徑的第一步的高度是0,則稱這條路徑是初始高度為0的路徑;否則,如果從起點開始連續上升的步中最后一步的高度為k,則稱這條路徑是初始高度為k的路徑,其中這些連續上升的步記為Uk,Uk中的第i步記為.長度為18且初始高度為4的Schr?der路徑,其中從起點開始連續上升的四步整體記為U4,并將這四步分別記為,如下圖所示:

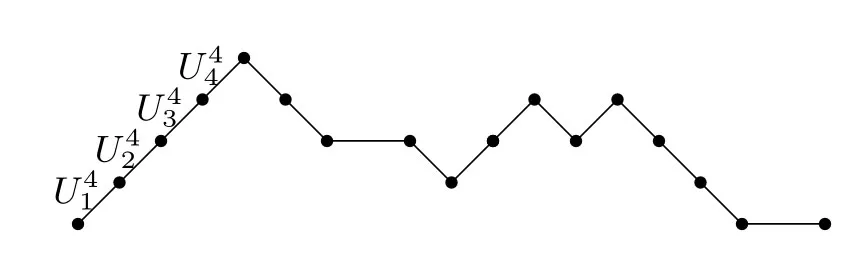
圖1 長度為18且初始高度為 4的 Schr?der路徑

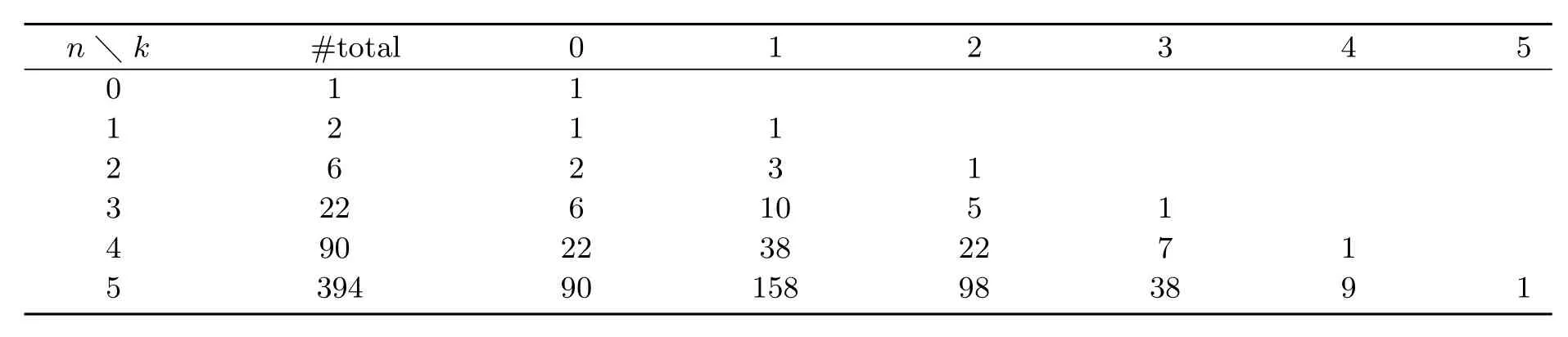
表1.1 長度小于12且不同初始高度k的Schr?der路徑的計數

定義 1.4長度為2n的小Schr?der路徑是一條x軸上不存在水平步的Schr?der路徑.

小 Schr?der路徑所組成的集合記為 Sn,其數量記為 sn.顯然,sn等于小 Schr?der數 (A001003[10]),即 1,1,3,11,45,···.長度為 2n且初始高度為 k的小 Schr?der路徑所組成的集合記為S(n,k),其數量記為s(n,k).長度小于12且不同初始高度k的小Schr?der路徑的計數如下表所示:

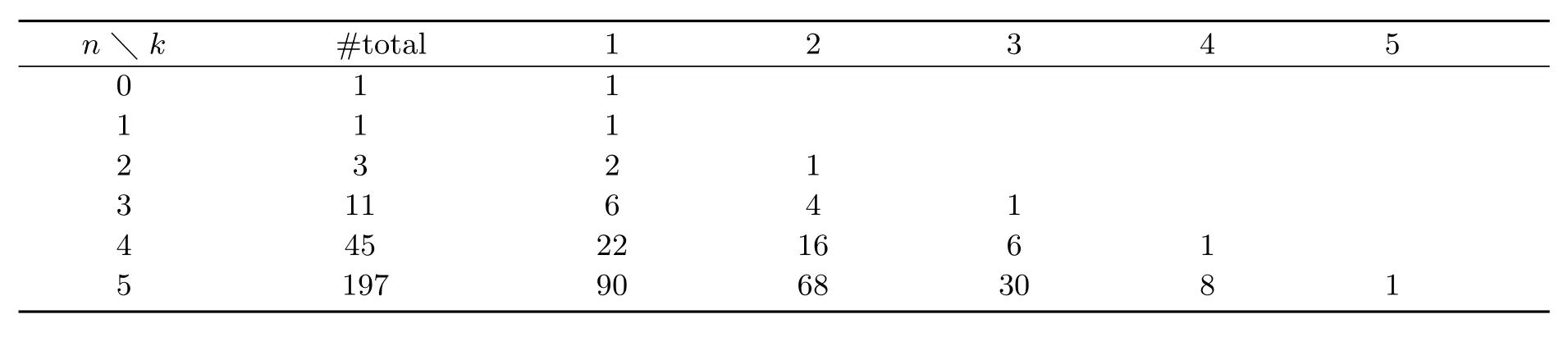
表1.2 長度小于12且不同初始高度k的小Schr?der路徑的計數

2 關于 Schrder路徑的幾個恒等式的組合證明

定理 2.1當n≥1,k≥0時,r(n,k)滿足下列遞推式:

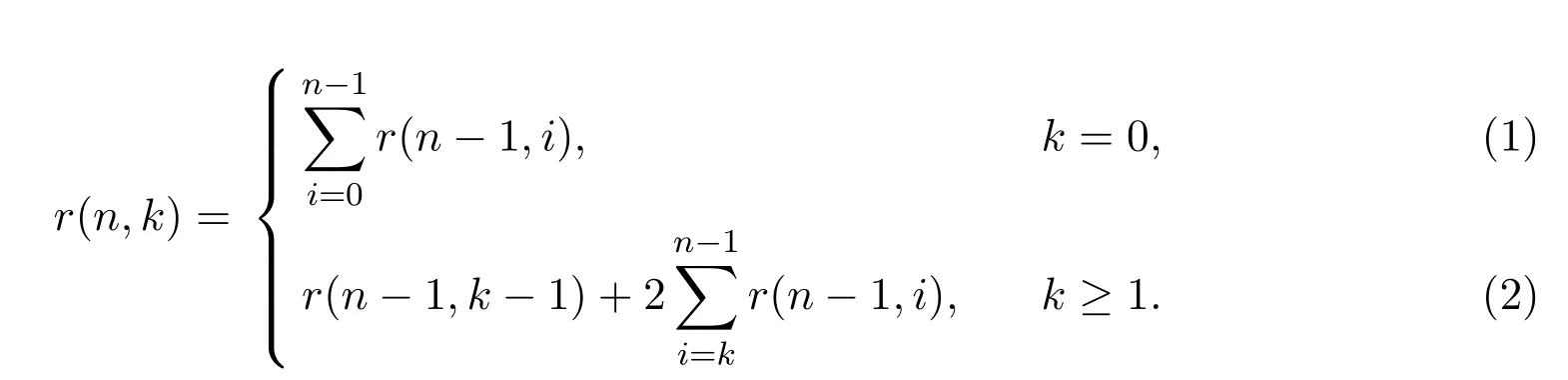
其中初始條件r(0,0)=1.

證明當k=0時,只需在所有長度為2(n?1)的 Schr?der路徑的起點插入一個 H 步,即可得到長度為2n且初始高度為0的Schr?der路徑.從而(1)式得證.

當k≥1時,采用數學歸納法.首先,給定一條長度為2m且初始高度為k的Schr?der路徑.

當m=1時,r(1,1)=1,顯然,(2)式成立.

當m=n?1時,假設

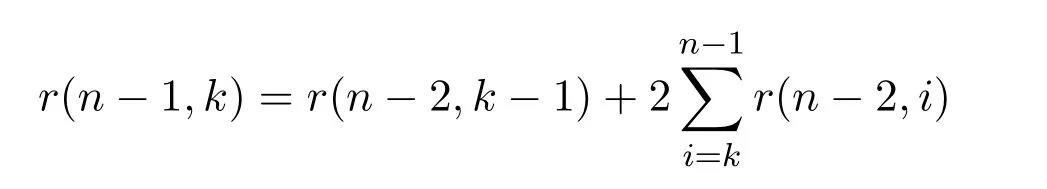
成立.

隨著“互聯網+”時代的到來，手機已成為人們生活中不可缺少的智能應用工具。隨著各種智能化、人性化手機軟件的開發，智能手機已經實現智能查詢、導航、交互、支付等多種功能，并在向更加智能化的方向發展。而在大學生群體中，智能手機更是必備的應用工具。據相關調查發現，目前高校大學生幾乎人人使用手機。除了生活中的應用外，智能手機以其便于攜帶、支持多媒體播放、實現信息互動的特性，使得高校學生在學習中也會普遍使用其上網查找學習資源，閱讀電子書籍，開展個性化的自主學習，與老師、同學交流互動等。

當 m=n時,給定一條長度為 2(n?1)的 Schr?der路徑,若其初始高度為 k?1,則在后插入UD,從而得到相應的長度為2n且初始高度為k的Schr?der路徑;若其初始高度為j(k≤j≤n?1),則在后插入一個DU或者一個H.即得到長度為2n且初始高度為 k 的 Schr?der路徑.

顯然,上述兩種情況的過程均是可逆的.故等式(2)成立。

定理 2.2當n≥1,r(n,k)滿足下列遞推式:

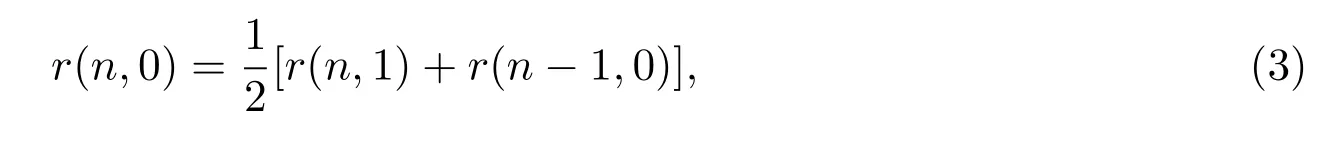
其中初始條件r(0,0)=1.

證明首先,將長度為2n且初始高度為0的Schr?der路徑的第一步進行二染色,該步分別記為H1、H2,且將染色后的路徑組成的集合記為R2(n,0).

給定集合R2(n,0)中的任意一條路徑 P,考慮以下變換.若路徑 P的第一步為 H1,則將H1變為UD;若路徑P的第一步為H2且第二步為H,則刪除H2;若路徑P的第一步為H2且第二步為U,則將H2U變為UH.由于R(n,1)中的路徑只能以UD或UH為起始步,而R(n,0)中的路徑只能以H 為起始步,故上述變換可逆.從而(2.2?1)式成立.

定理2.3當n≥1,k≥1時,r(n,k)滿足下列遞推式:其中初始條件r(0,0)=1.

第一種情況,給定長度為2n且初始高度為k+1的Schr?der路徑時,該路徑的第k+2步可能是D或H,分別將變為DU,變為HU,其它步保持不變.

第二種情況,給定長度為 2 (n?1)且初始高度為 k 的 S chr?der路徑,在后插入 D U或H.

第三種情況,給定長度為2(n?1)且初始高度為 k ?1的Schr?der路徑中,在后插入UD.

反之,若給定一條長度為2n且初始高度為k的Schr?der路徑.根據該路徑的第k+1、k+2步,可以將Schrder路徑分成以下六種:

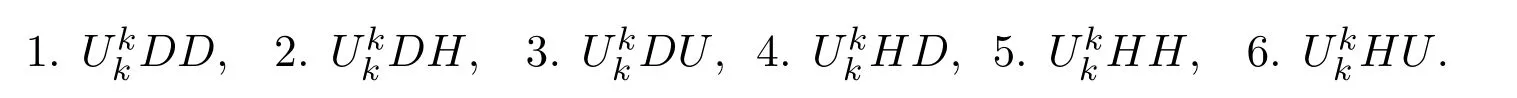
如下圖所示:

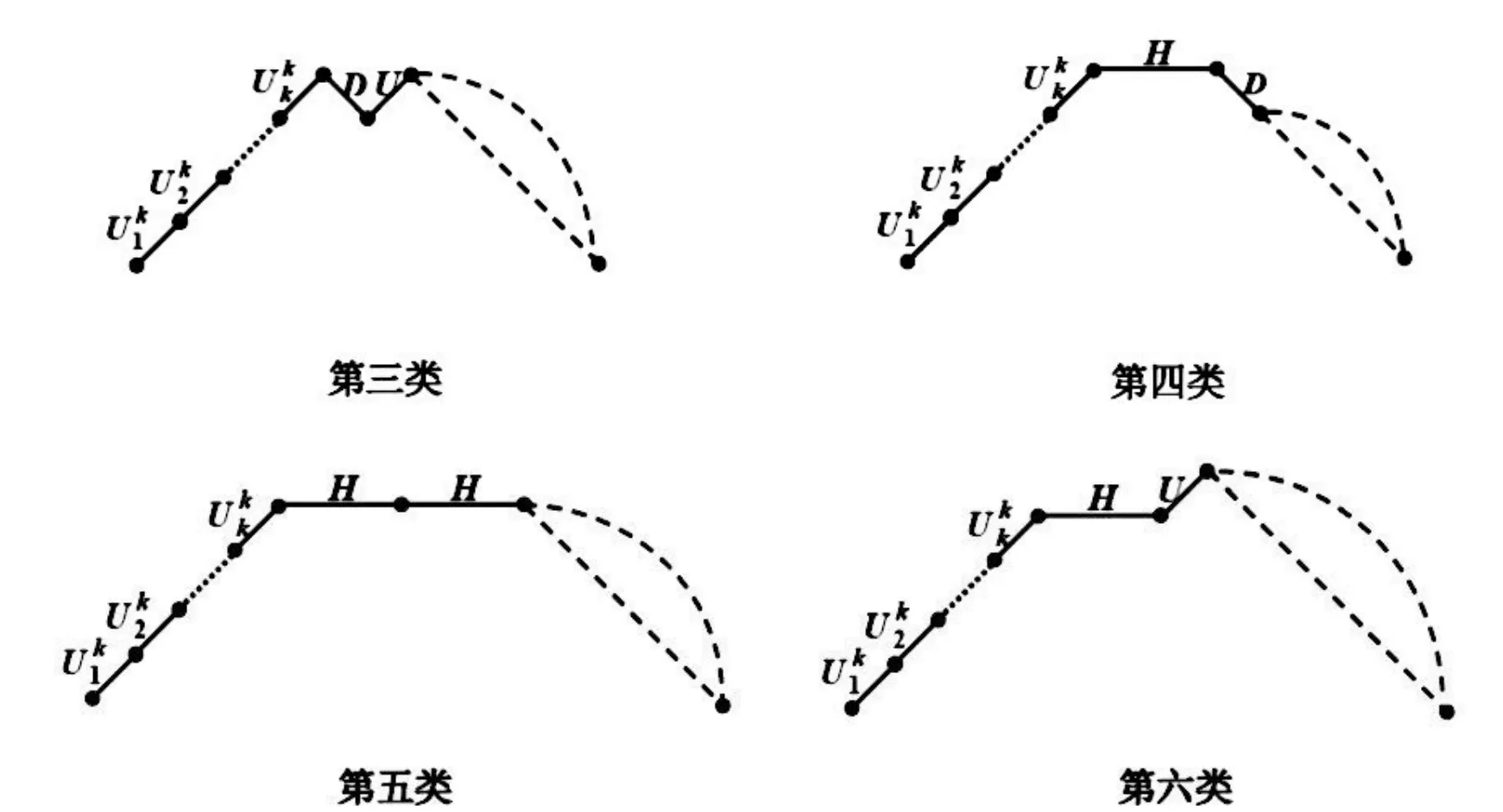
圖2 長度為2n且初始高度為k的六種不同的Schr?der路徑(k/=0)

綜上,等式(4)成立.

推論2.1當n≥1,k≥1時,s(n,k)有下式成立:

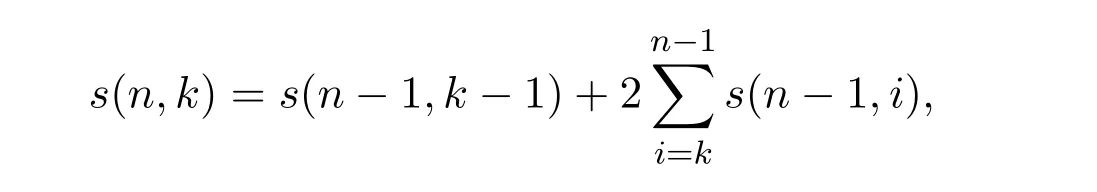
其中初始條件s(0,0)=1.

推論2.2當時,s(n,k)有下式成立:

其中初始條件s(0,0)=1.

[1]Schr?der E.Vier combinatorische Probleme[J].Z.fur Math.Physic.,1870,15:361-376.

[2]Shapiro L W,Sulanke R A.Bijections for the Schr?der numbers[J].Mathematics Magazine,2000,73(5):369-376.

[3]Deutsch E.A bijective proof of the equation linking the Schr?der numbers,little and small[J].Discrete Math.,2001,241:235-240.

[4]Huh J S,Park S K.Generalized small Schr?der numbers[J/OL].Electronic J.Combin.,2015[2017-07].http://www.combinatorics.org.

[5]Yan S H F.From(3,2)-Motzkin paths to Schr?der paths[J/OL].J.Integer Sequences,2007[2017-07].http://www.emis.de/journals/JIS/vol10.html.

[6]Song C W.The generized Schr?der theory[J/OL].Electronic J.Combin.,2005[2017-07].http://www.combinatorics.org.

[7]Chen Z J,Zhao S.Two bijections on weighted Motzkin paths[J].Communications In Mathematical Research,2017,33(2):149-159.

[8]Shapiro L W,Wang C J.A bijection between 3-Motzkin paths and Schr?der paths with no peak at odd height[J/OL].J.Integer Sequences,2009[2017.07].http://www.emis.de/journals/JIS/vol12.html.

[9]Pergola E,Sulanke R A.Schr?der triangles,paths,and parallelogram polyominoes[J].J.Integer Sequences,1998[2017-07].http://www.emis.de/journals/JIS/vol1.html.

[10]Sloane N J A.The On-Line Encyclopedia of Integer Sequences[EB/OL].The OEIS Foundation Inc.,2014[2017-07].http://oeis.org.

The combinatorial proofs of several recurrences about the enumeration of Schr?der paths

Yin Pengjun
(School of Mathematics,Beijing Technology and Business University,Beijing 100048,China)

By analyzing the characteristics of di ff erent steps in the Schr?der paths,we studied the Schr?der paths with di ff erent initial height and provided the combinatorial proofs of several recurrences of the enumeration of Schr?der paths.

Schr?der path,little Schr?der path,initial height

O157.1

A

1008-5513(2017)05-0530-06

10.3969/j.issn.1008-5513.2017.05.011

2017-08-03.

國家自然科學基金(11601020;11501014);北京市委組織部優秀人才項目(2013D005003000012);2017商科特色項目(19005757053).

尹鵬君(1992-),碩士研究生,研究方向：組合計數.

2010 MSC:05A15