某類具有對稱共軛點的倒星象函數的三階Hankel行列式上界估計

張海燕, 馬麗娜, 王煥

(赤峰學院數學與統計學院,內蒙古 赤峰 024000)

某類具有對稱共軛點的倒星象函數的三階Hankel行列式上界估計

張海燕, 馬麗娜, 王煥

(赤峰學院數學與統計學院,內蒙古 赤峰 024000)

利用從屬關系引入了一類關于對稱共軛點的倒星象函數類 Ss?,c(A,B),用Toeplitz行列式討論了上述函數類的三階Hankel行列式H3(1),得到了該行列式的上界估計.其結果改進并推廣了一些已有結論.

倒星象函數;對稱共軛點;三階Hankel行列式;上界估計

1 引言

設S表示單位圓盤D={z∈C:|z|＜1}內單葉解析且具有如下形式的函數族:

設P表示單位圓盤D={z∈C:|z|＜1}內具有如下形式且滿足條件Re p(z)＞0的函數族:

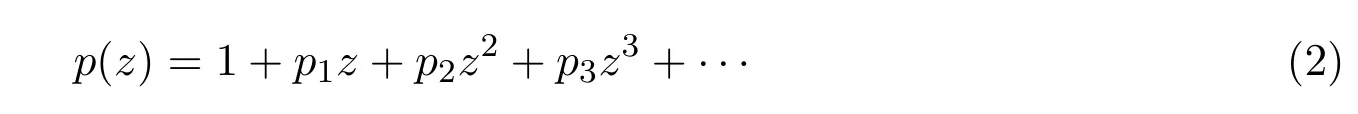
由文獻[1]中的結論易知,對于函數p(z)∈P,存在Schwarz函數ω(z),使得

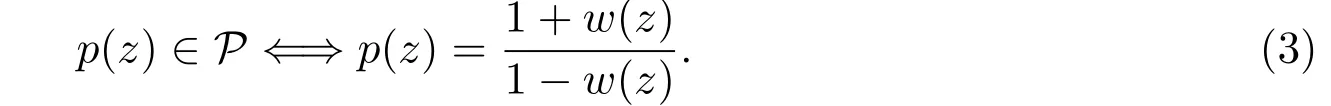
定義1.1[2]設函數f(z)和g(z)在單位圓盤D內解析.如果存在D內的Schwarz函數ω(z),滿足:ω(0)=0,|ω(z)|＜ 1且 f(z)=g(ω(z)),則稱 f(z)從屬于 g(z),記為 f(z)? g(z).特別地,如果g(z)在D內單葉,則

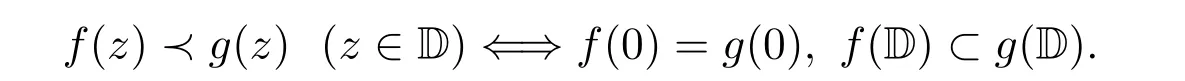
設函數f(z)∈S,若滿足

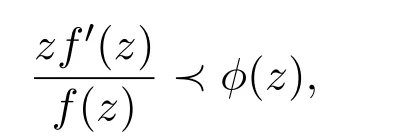
則稱函數 f(z)屬于函數類 S?(?),其中 ?(z)∈P.函數類 S?(?)和相應的凸函數類 K(?)詳見文獻[3].

1959年,Sakaguchi在文獻[4]中引入關于對稱點的星象函數類S?,f∈S?當且僅當

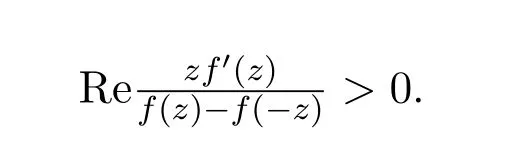
1987年,El-Asha和 Thomas在文獻 [5]中引入并分別研究了關于共軛點的星象函數類和關于對稱共軛點的星象函數類,分別滿足如下條件

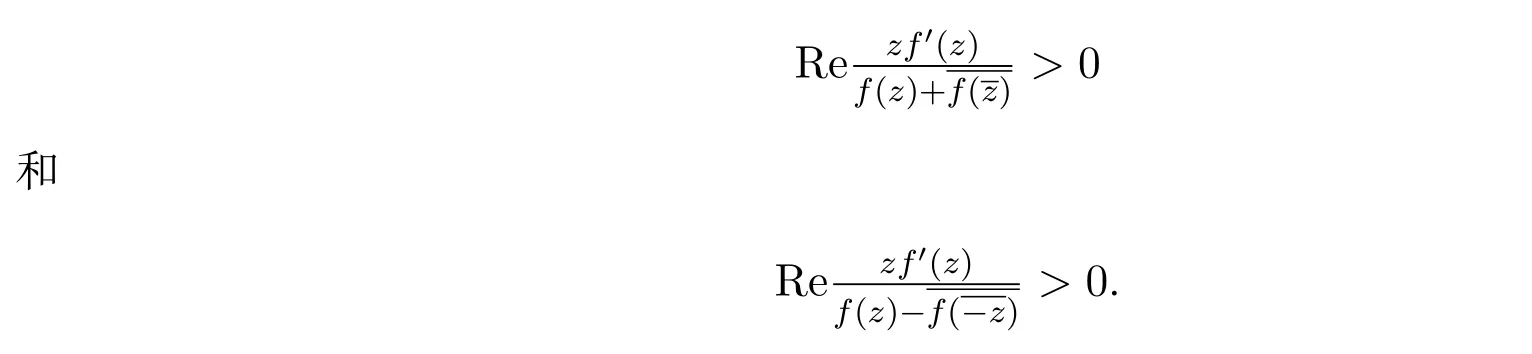
利用從屬關系,本文引入了關于對稱共軛點的倒星象函數類S?sc(A,B)如下.

定義1.2設是具有(1)的形式且滿足下面條件的函數全體,

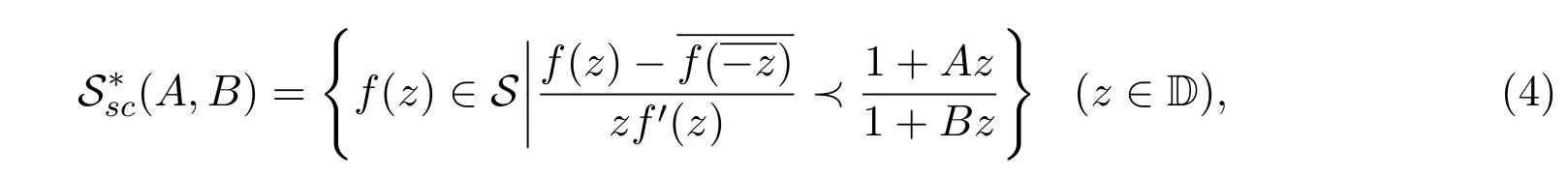
其中?1≤B＜A≤1.

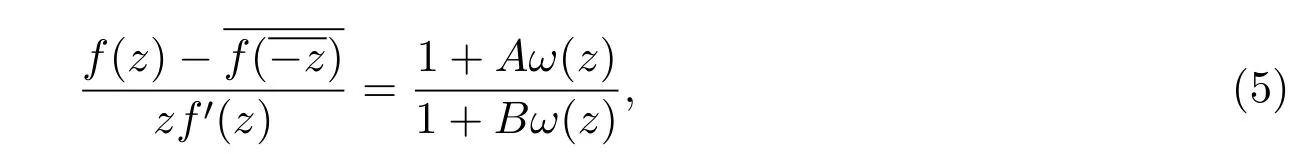
其中ω(z)是單葉解析函數,且滿足

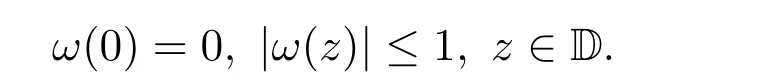
1976年,Noonan和Thomas[6]定義了函數f的q階Hankel行列式:

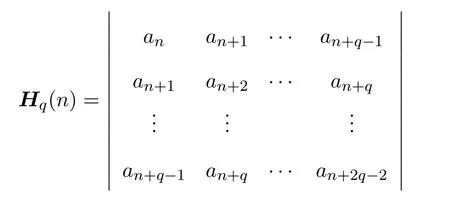
其中a1=1,n≥1,q≥1.

因為 f∈S,a1=1,故有

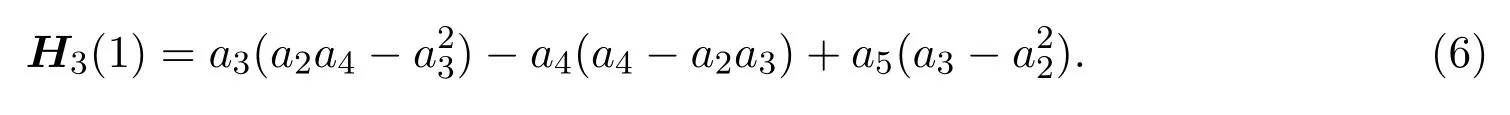
其中 H2(1)的上界估計即是經典的Fekete-Szeg不等式[7].

近年來,越來越多的學者對Hankel行列式的研究產生了濃厚的興趣.Noonan和Thomas研究了p葉函數的二階Hankel行列式[6],Noor在文獻[8]中研究了星象函數的行列式Hq(n),并確定了當n→∞時,行列式Hq(n)的增長率.其他相關研究詳見文獻[9-11].受以上啟發,張海燕、湯獲等在文獻[12]中研究了一類與對稱點有關的一類解析函數Ms(α,μ,A,B)的三階Hankel行列式H3(1),并得到了其上界估計.利用類似的方法,本文研究了與對稱共軛點有關的一類倒星象函數S?s,c(A,B)的三階Hankel行列式H3(1),給出了該行列式的上界估計.

2 主要結果

除非特別說明,在本文中,我們總假設?1≤B＜A≤1.為了證明本文結論,需要如下引理.

引理 2.1[2]如果p(z)∈P,則引理 2.2[13]如果p(z)∈P,則存在復數x,z,滿足 |x|≤1,|z|≤1,使得

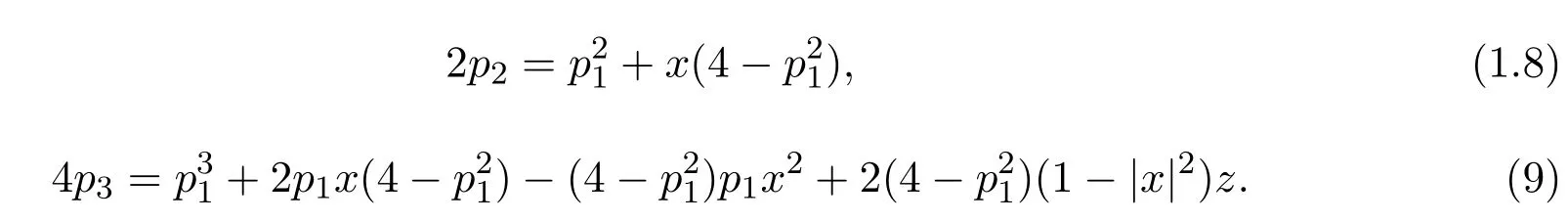
定理 2.1設f∈,則

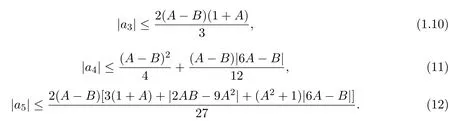
證明設,則由定義1.2和(5)式,可得

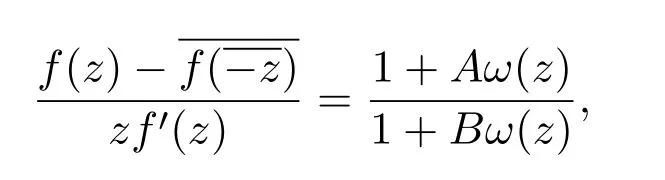
其中 ω(z)是 Schwarz函數且滿足 ω(0)=0,|ω(z)|≤1,z∈D.令

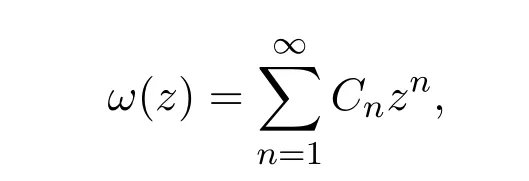
則有

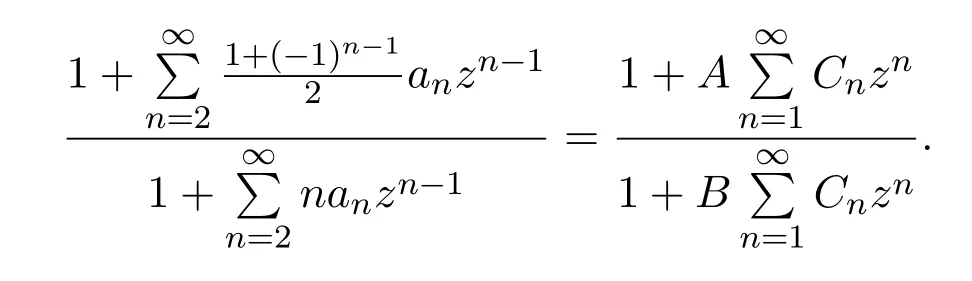
進而可得

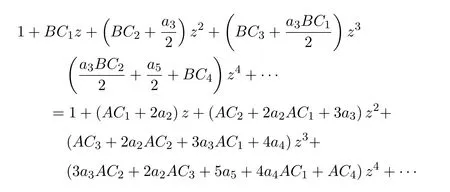
分別比較上式中z,z2,z3,z4的系數,易得

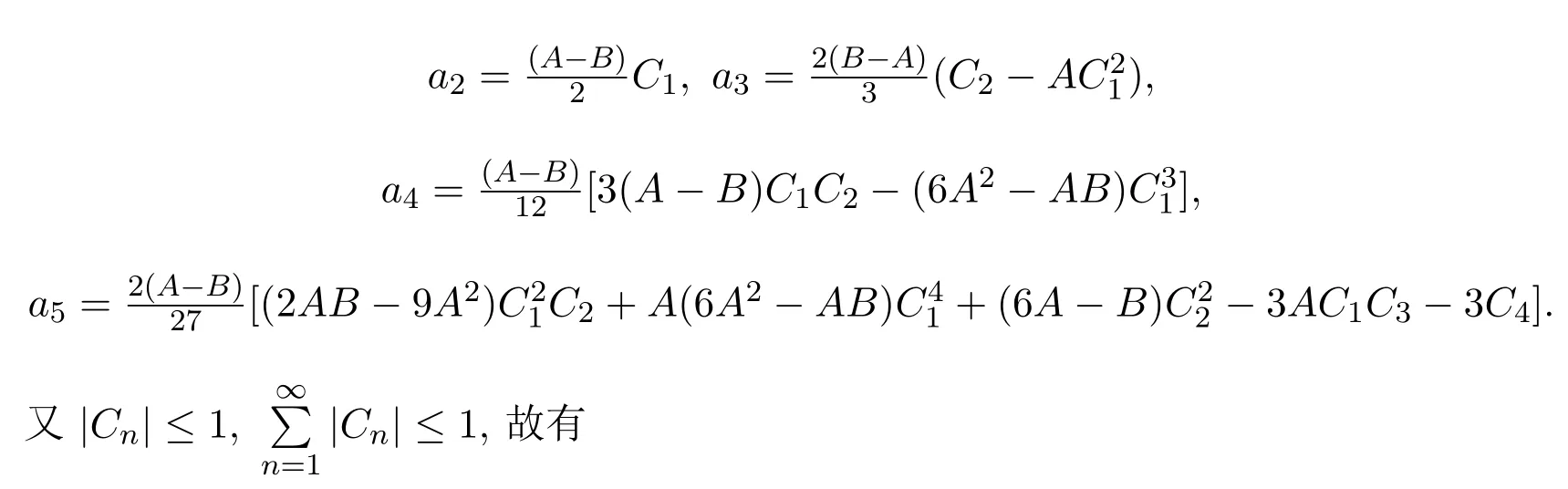
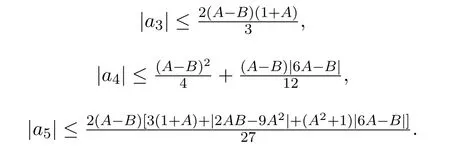
定理2.1得證.

定理 2.2若,則有

證明設,由從屬定義和(1.5)式可得

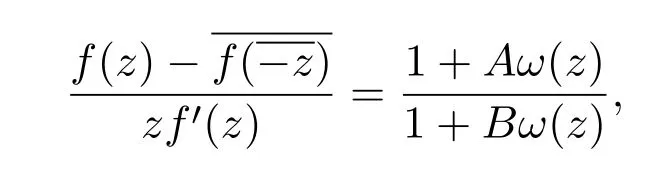
其中 ω(z)是單葉解析函數,且滿足ω(0)=0,|ω(z)|≤1,z∈D.令

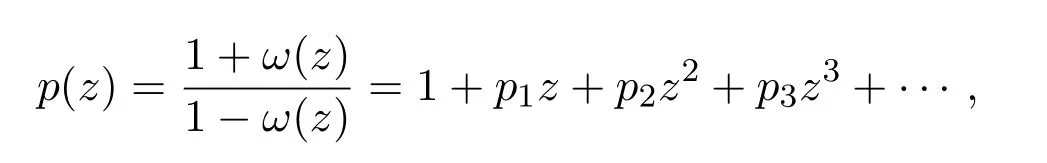
顯然 p(z)∈P,且

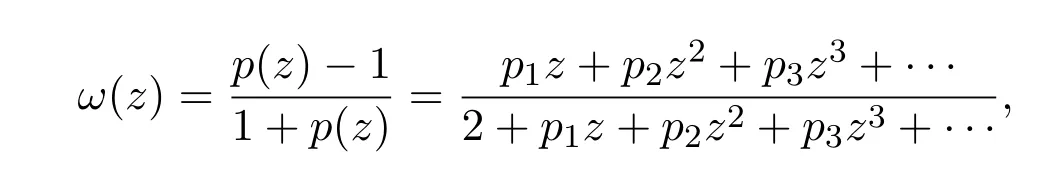
因此有

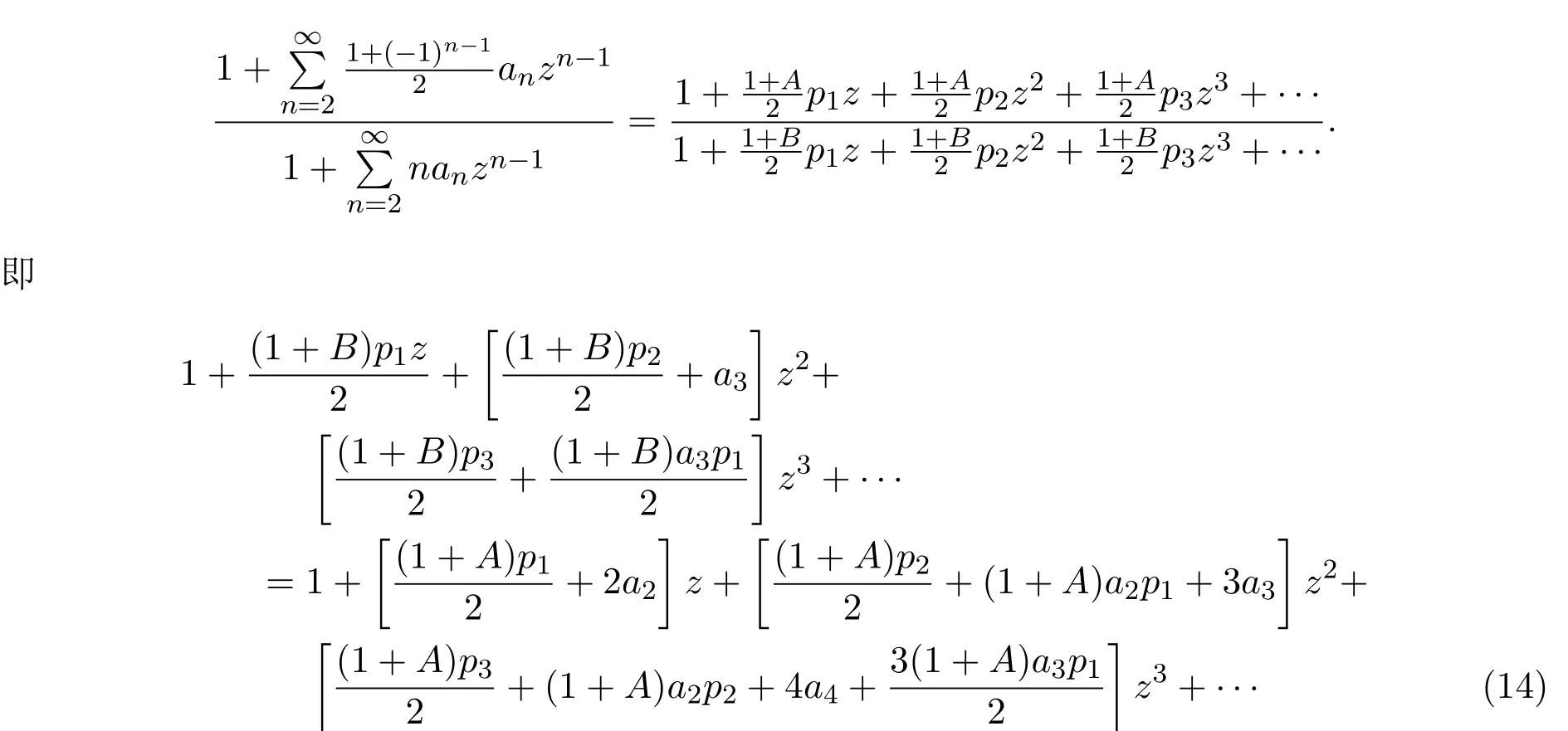
分別比較(14)式中等號兩邊z,z2,z3的系數,得

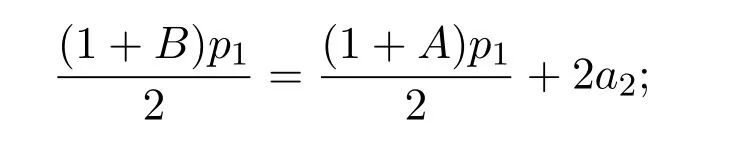
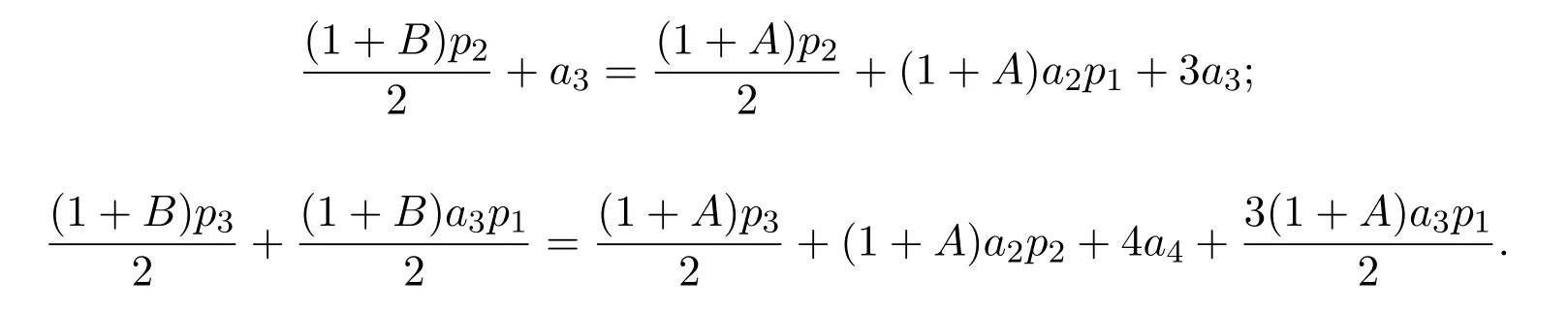
于是,有

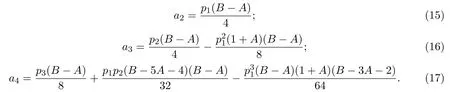
從而,有

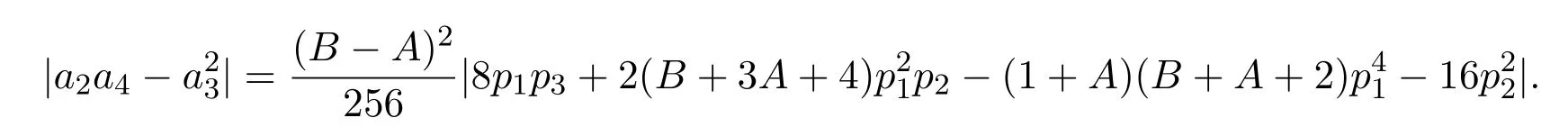
設

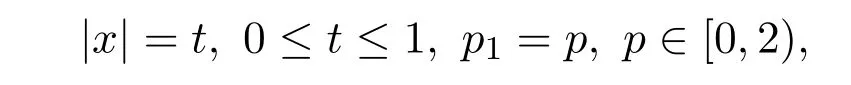
又因為|z|≤1,則由三角不等式和引理2.2,可得

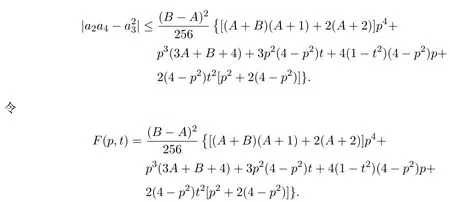
進而,有

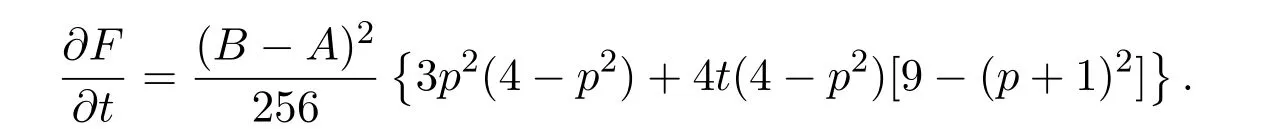
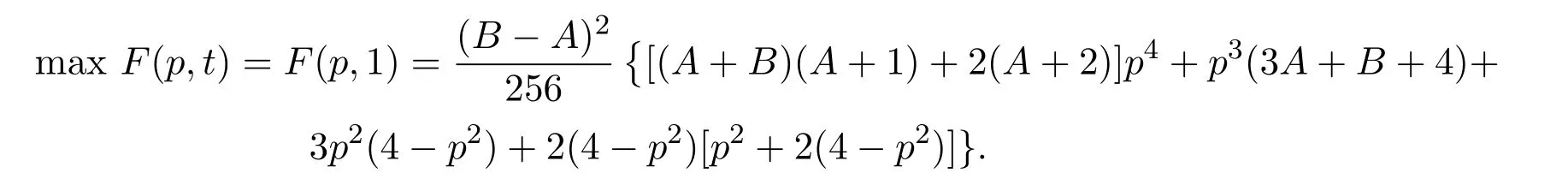
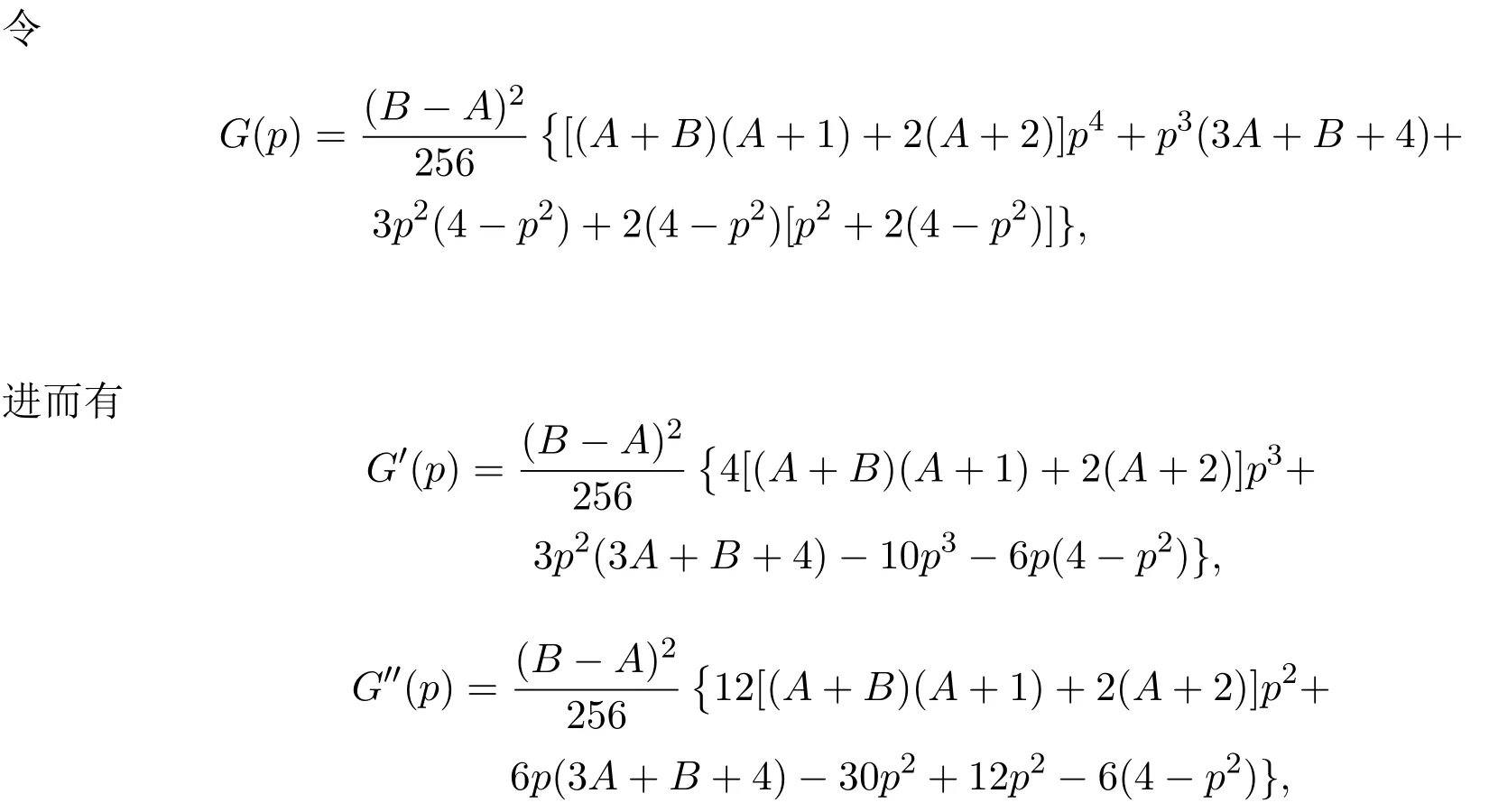
顯然 p=0是 G(p)的根.又因為 G′′(0)＜ 0,所以 G(p)在 p=0處取到最大值.因此函數F(p,t)在t=1,p=0處取得最大值,即

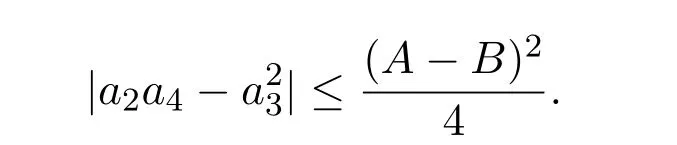
定理2.2得證.

定理2.3若,則有

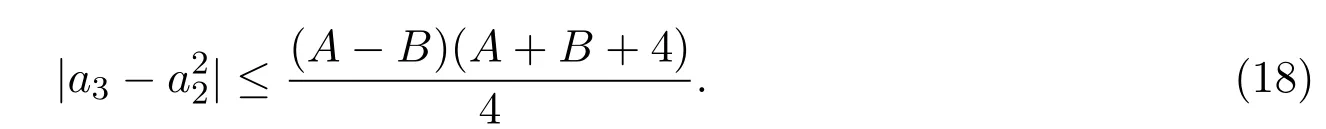
證明此定理的證明方法與定理2.2類似,在此省略其證明過程.

定理2.4若,則有

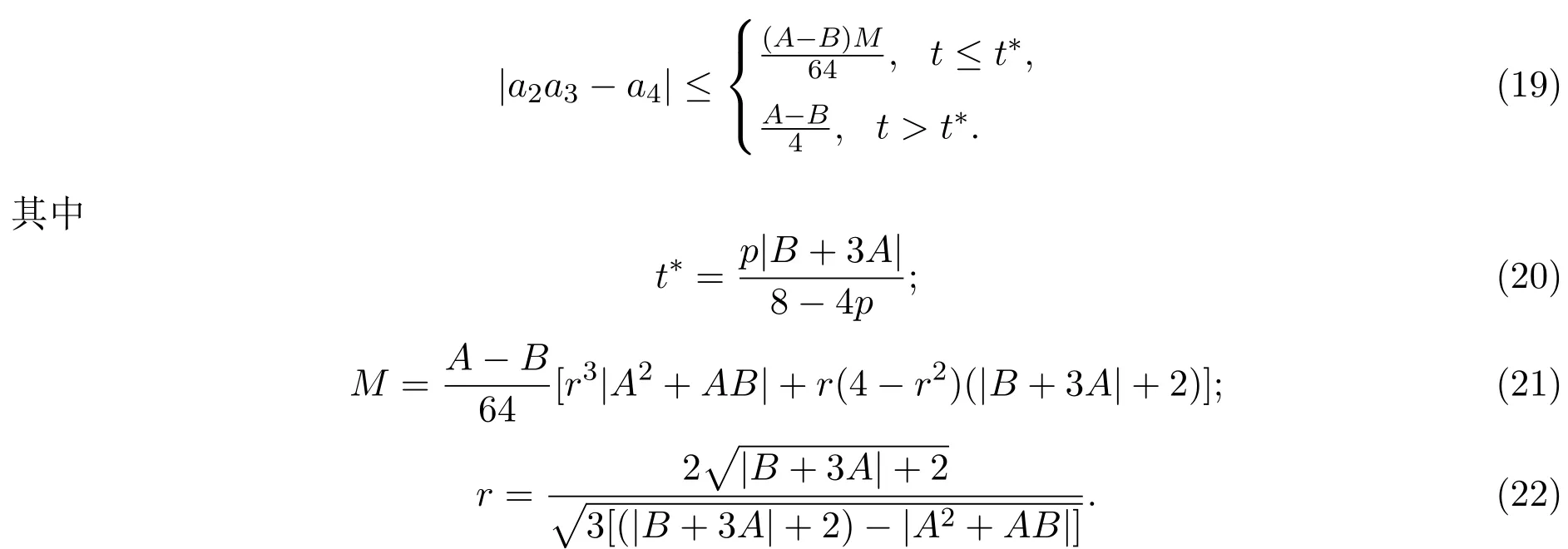
證明由(15),(16),(17)式,可得

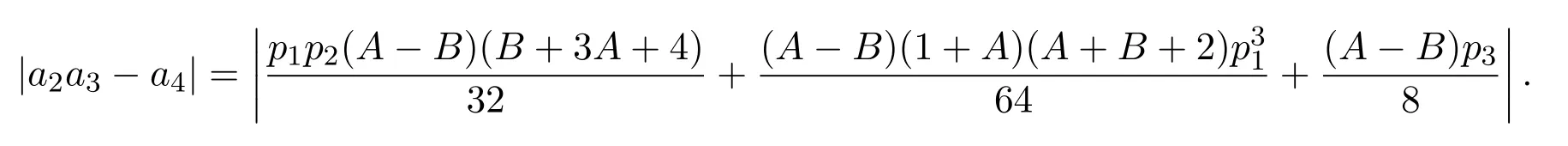
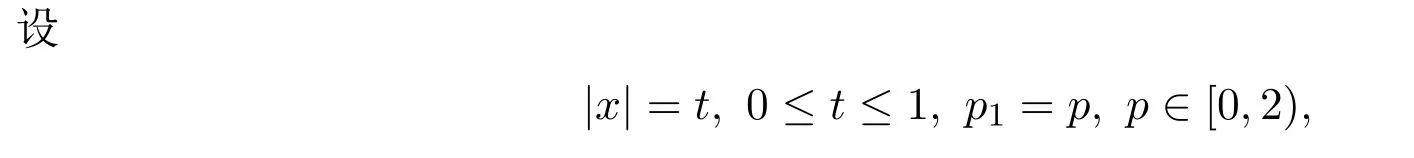
又因為|z|≤1,則由三角不等式和引理2.2,可得

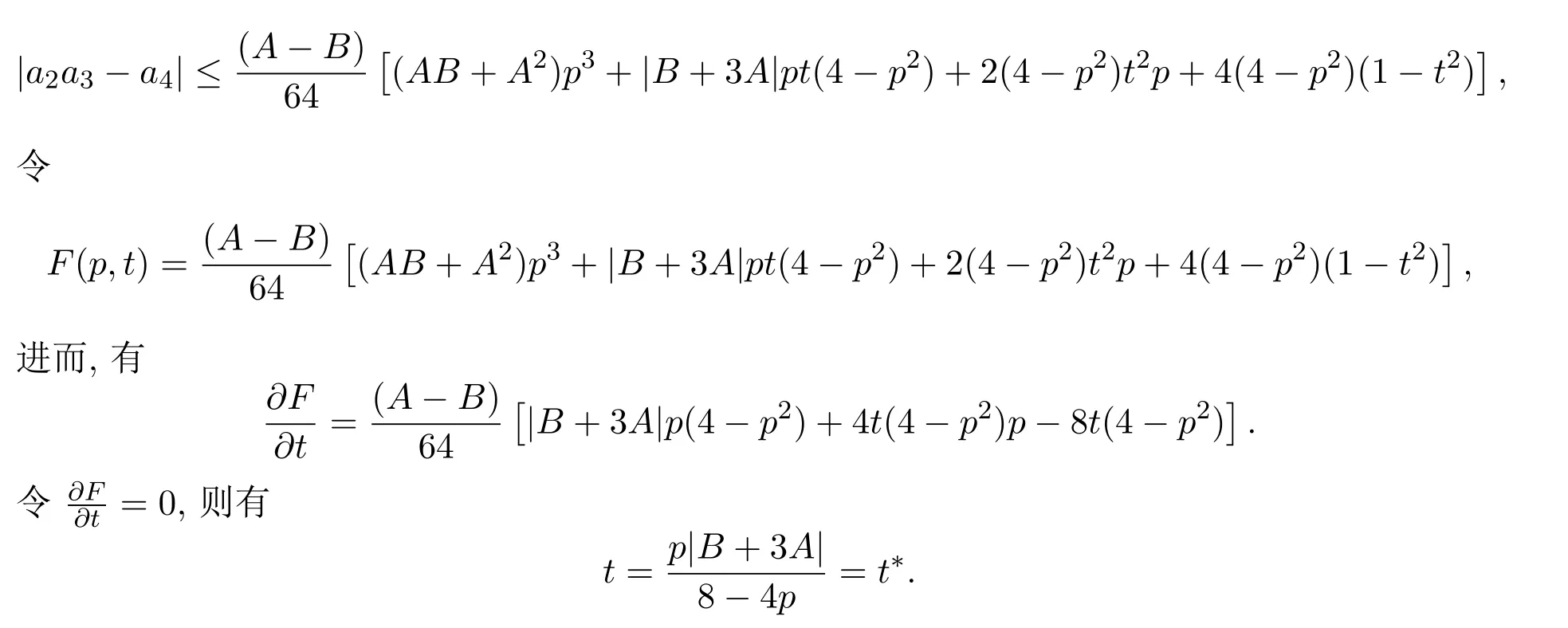
下面分兩種情況進行討論:

(1)當 t ＞ t?時,＜0,函數F(p,t)關于t嚴格單調遞減,F(p,t)在t=0取最大值,即

顯然 p=0是 G(p)的根.又因為 G′′(0)＜0,所以G(p)在 p=0處取到最大值.因此函數F(p,t)在t=0,p=0處取得最大值,即

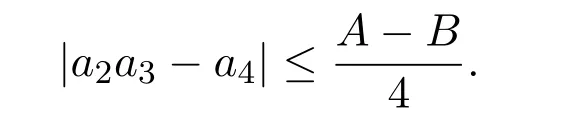
(2)類似地,當t≤t?時,≥0,函數F(p,t)關于t單調遞增,F(p,t)在t=1處取得最大值,即

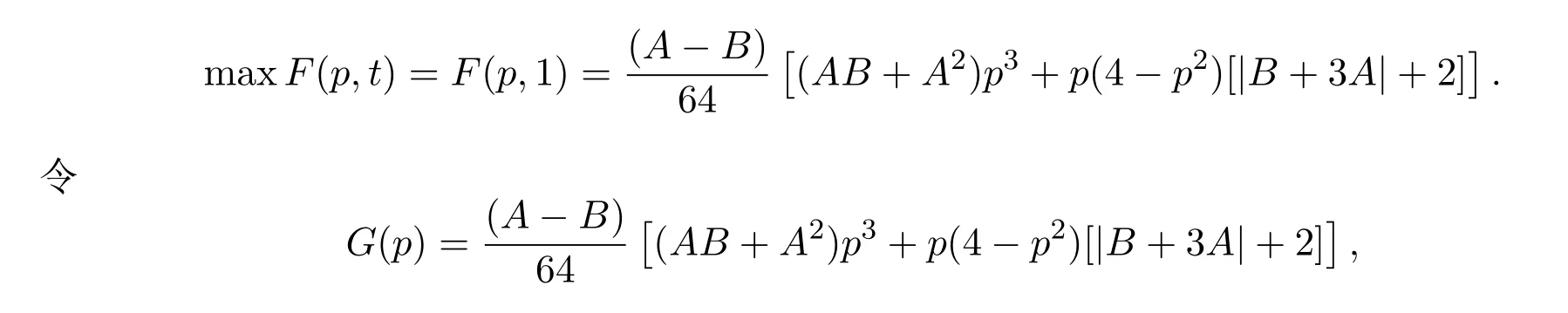
進而,有

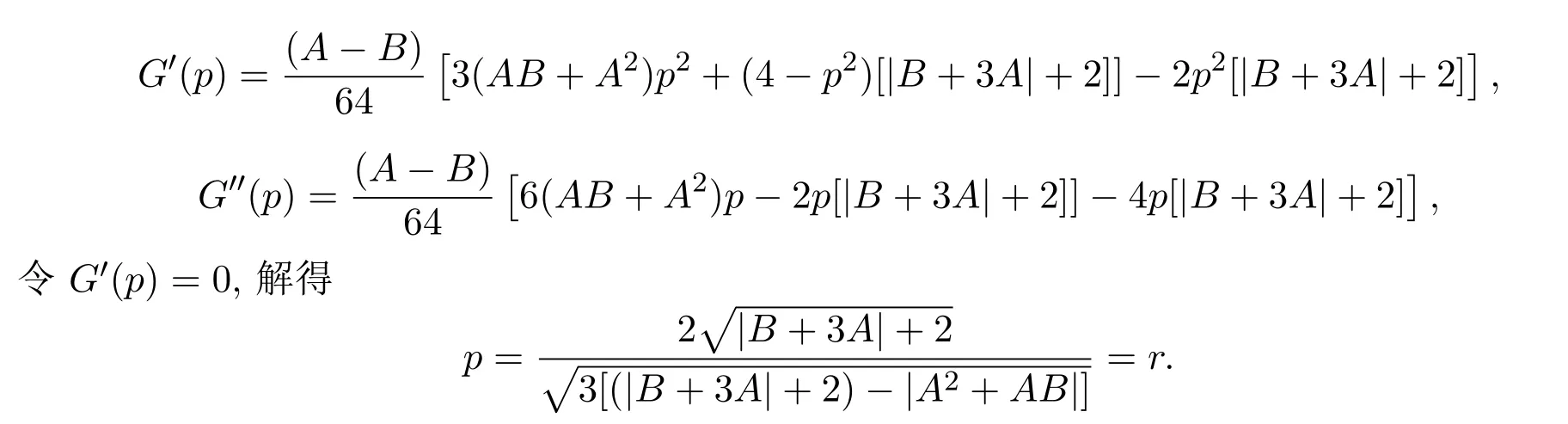
又因為G′′(r)＜0,所以G(p)在p=r處取到最大值.因此函數F(p,t)在t=1,p=r處取得最大值,即

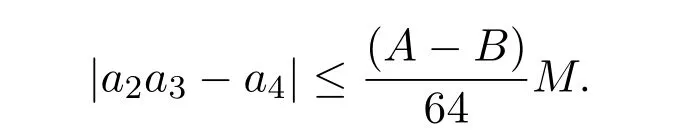
綜上可知,定理2.4得證.

定理 2.5設,則有

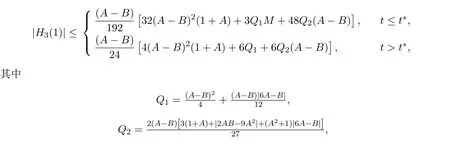
t?,M,r分別由 (20),(21),(22)式給出.

證明因為

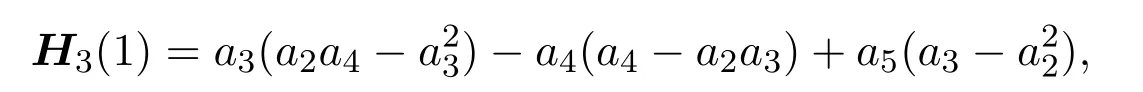
故由三角不等式可得

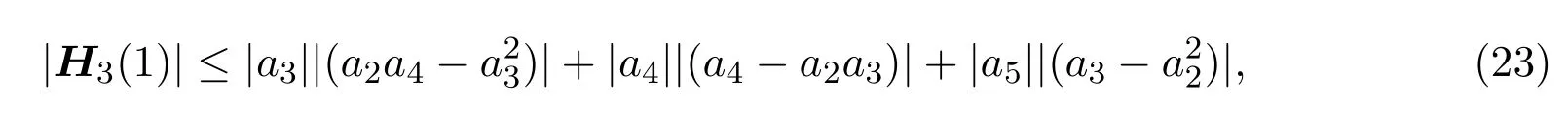
將(10),(11),(12),(13),(18),(19)式代入到(23)式,即得定理2.5的結論.

[1]Graham I,Kohr G.Geometric Function Theory in One and Higher Dimensions[M].New York:Marcel Dekker,Inc.,2003.

[2]Duren P L.Univalent Functions[M].New York:Springer Verlag,1983.

[3]Sakaguchi K.On a certain univalent mapping[J].J.Math.Soc.Japan,1959,11:72-75.

[4]El-Ashah R M,Thomas D K.Some subclasses of close-to-convex functions[J].J.Ramanujan Math.Soc.,1987,74(4):85-100.

[5]Halim S A.Functions starlike with respect to other points[J].Intermat J.Math.Math.Sci.,1991,14(3):451-456.

[6]Noonan J W,Thomas D K.On the second Hankel determinant of areally mean p-valent functions[J].Transactions of the American Mathematical Society,1976,223(2):337-346.

[7] Fekete M,SzegG.Eine benberkung uber ungerada schlichte funktionen[J].J.London Math.Soc.,1933,8(2):85-89.

[8]Noor K I.Hankel determinant problem for the class of functions with bounded boundary rotation[J].Rev.Roumaine Math.Pures Appl.,1983,28(8):731-739.

[9]Singh G.Hankel determinant for new subclasses of analytic functions with respect to symmetric points[J].Int.J.of Modern Mathematical Sciences,2013,5(2):67-76.

[10]Raza M,Malik S N.Upper bound of the third Hankel determinant for a class of analytic functions related with lemniscate of bernoulli[J].Journal of Inequalities and Applications,2013,2013(1):1-8.

[11]Sudharsan T V,Vijayalakshmi S P.Adolf Stephen B.Third Hankel determinant for a subclass of analytic univalent functions[J].Malaya J.Mat.,2014,2(4):438-444.

[12]張海燕,湯獲,馬麗娜.一類解析函數的三階 Hankel行列式上界估計[J].純粹數學與應用數學,2017,33(2):211-220.

[13]Libera R J,Zlotkiewicz E J.Coefficients bounds for the inverse of a function with derivative in positive coefficients[J].Proc.Amer.Math.Soc.,1983,87(2):251-257.

The estimate of upper bound of third Hankel determinant for a class of reciprocal starlike functions with respect to symmetric conjugate points

Zhang Haiyan,Ma Lina,Wang Huan
(School of Mathematics and Statistics,Chifeng University,Chifeng 024000,China)

In this paper,we introduce a class of reciprocal starlike functions with respect to symmetric conjugate points use affiliation,denoted by.we investigate the Hankel determinant H3(1)for this class functions with Toeplitz determinant and obtain the estimate of upper bound of the above determinant.The results present here improve and generalize some known results.

reciprocal starlike functions,symmetric conjugate points,third Hankel determinant,upper bound

30C45,30C50

A

1008-5513(2017)05-0503-10

10.3969/j.issn.1008-5513.2017.05.008

2017-07-07.

國家自然科學基金(11561001;11761006);內蒙古自治區高等學校科學研究項目(NJZY16251).

張海燕(1981-),碩士,講師,研究方向：算子代數與復分析.

2010 MSC:30C45,30C55