帶有R-S積分邊值條件的分數階朗之萬方程的解的存在性

王西麗, 周宗福

(安徽大學數學科學學院,安徽 合肥 230601)

帶有R-S積分邊值條件的分數階朗之萬方程的解的存在性

王西麗, 周宗福

(安徽大學數學科學學院,安徽 合肥 230601)

研究一類帶有 R-S積分邊值條件的非線性分數階朗之萬方程邊值問題.利用Leray-Schauder非線性抉擇和Leray-Schauder度理論,得到幾個新的存在性結果.最后給出一個例子來證明主要結論的應用性.

分數階朗之萬方程;積分邊值條件;Leray-Schauder度理論;Leray-Schauder非線性抉擇

1 引言

朗之萬方程是由朗之萬在1908年描述布朗運動時提出的[1].在他的著作中牛頓第二定律應用于布朗粒子時的隨機物理運動稱之為朗之萬方程.朗之萬方程已經被廣泛的用來描述波動環境下的物理現象的演化[2].分數階朗之萬方程可以看作是整數階朗之萬方程的拓展,現在已經成為微分方程的研究熱點[3-5].近來,分數階微分方程的問題引起了許多專家的興趣[6-7].

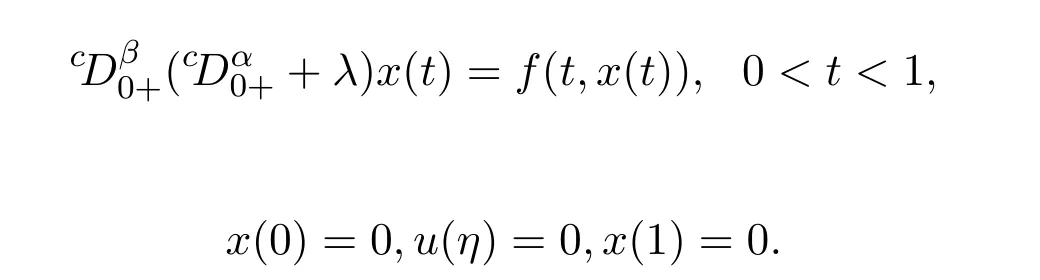
2012年,文獻[8]研究了三點邊值問題的朗之萬方程的解的存在性:其中0＜α≤1,1＜β≤2,和是開普特分數階導數,λ是實數.利用壓縮映射原理和Guo-Krasnoselskii錐不動點定理,得到幾個解的存在性證明.

2016年,文獻[9]研究了下列的分數階朗之萬方程的無窮多點邊值問題:

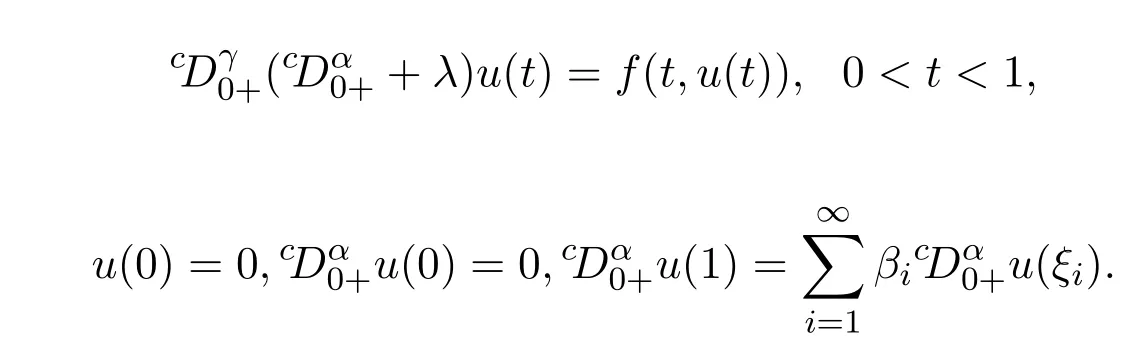
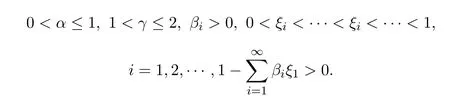
利用Leray-Schauder非線性抉擇和Leray-Schauder度理論可以得到一個獨特的滿足上述開普特分數階微分方程邊值問題解的存在性.

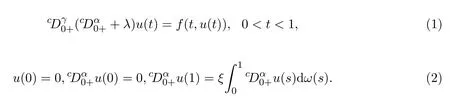
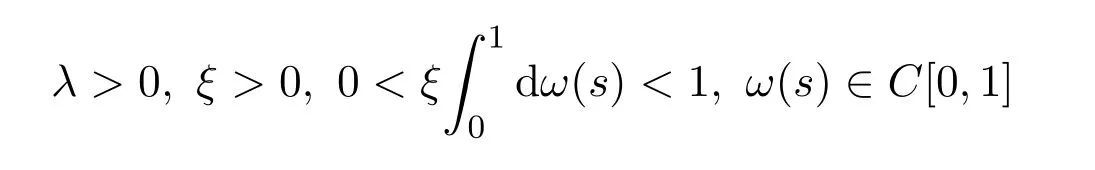
是連續不減的.

本文利用Leray–Schauder非線性抉擇和Leray–Schauder度理論研究以下的帶有R-S積分邊界條件的分數階朗之萬方程邊值問題,得到此邊值問題(1)和邊值問題(2)的解存在性的若干結果[11-12].

2 預備知識

定理 2.1Riemann-Liouville分數階積分算子的階q＞0,函數x(t)存在以下定義:

定理 2.2秩為q的分數階開普特微分方程,有連續可微的函數x:[0,+∞]→R,存在如下定義:

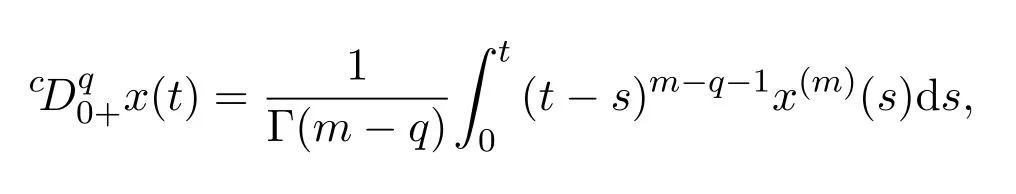
其中

并且[q]表示q的整數部分.

引理 2.1令,則u(t)是如下分數階朗之萬微分方程線性邊值問題:

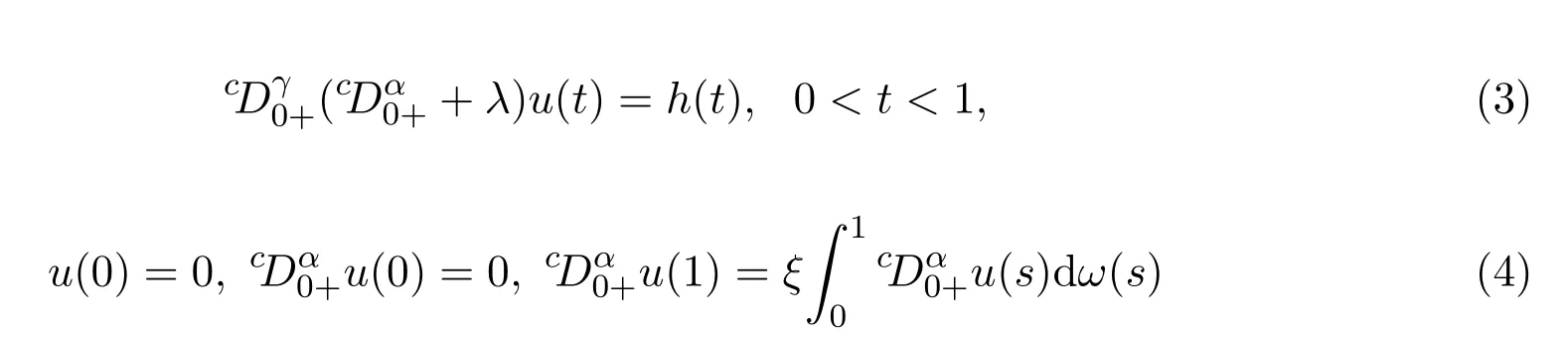
的解的充分必要條件是

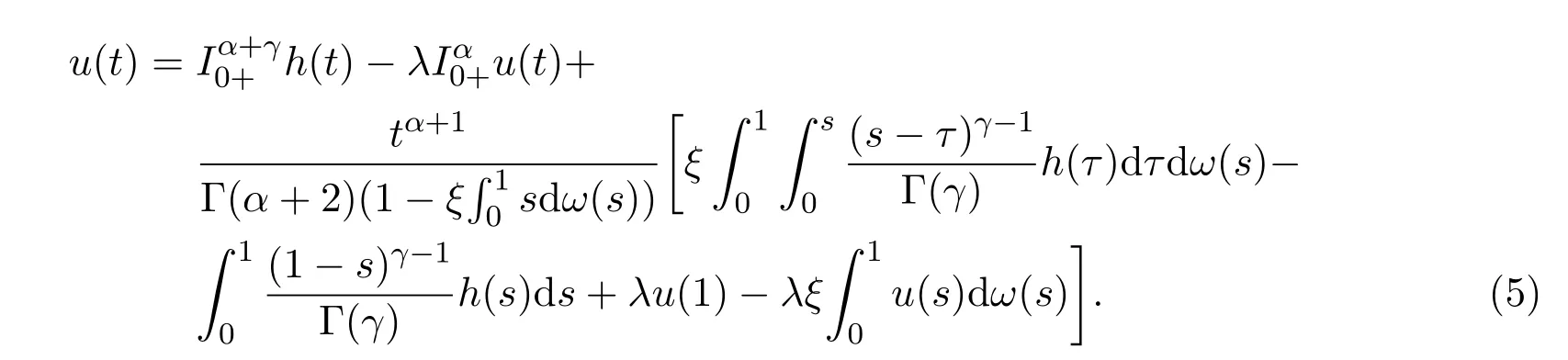
證明由于1＜γ≤2,故由以及(3)引理(2.1)可知,

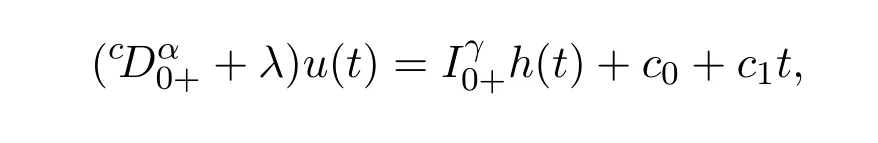
其中 c0,c1∈R.

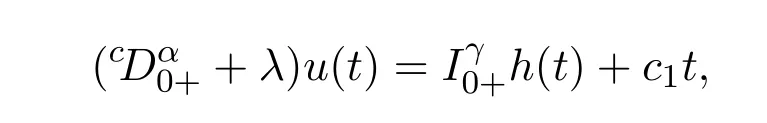
因此,

同理,由于0＜α＜1可得

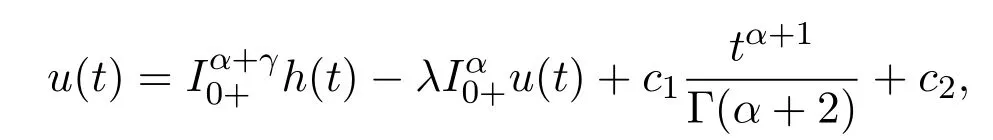
其中c2∈R.

由邊值條件u(0)=0,所以可以得到c2=0.因此,方程存在通解(3)滿足:

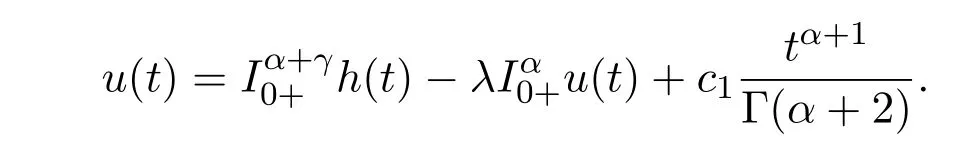
由邊值條件

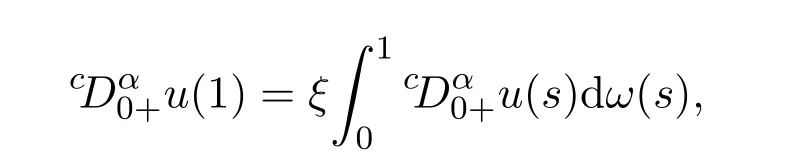
可得

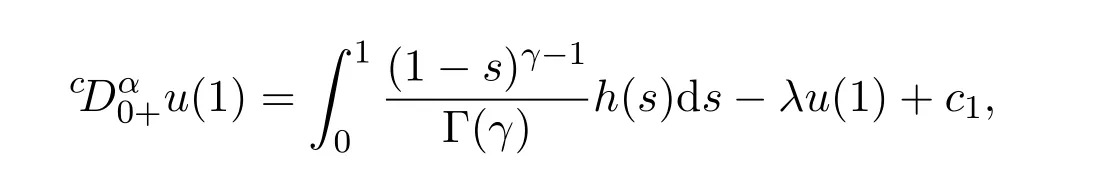
并且

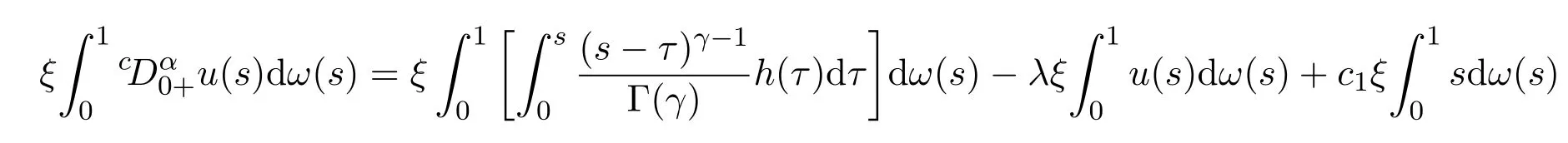
因此可知

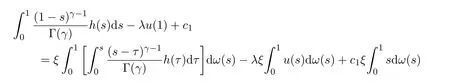
從而推導出

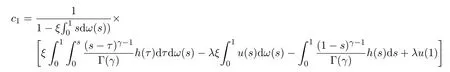
所以,u(t)滿足:

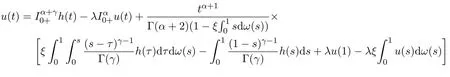
相反的,如果u(t)滿足(5),則

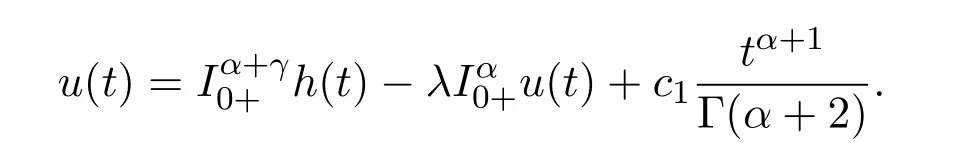
其中

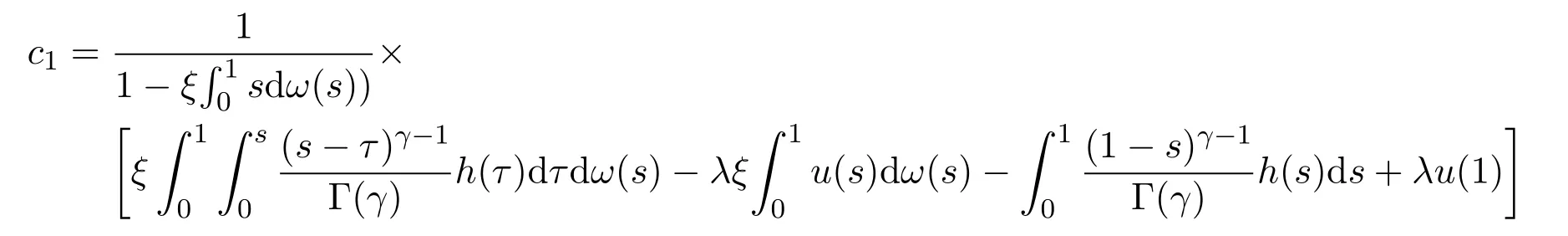
可得

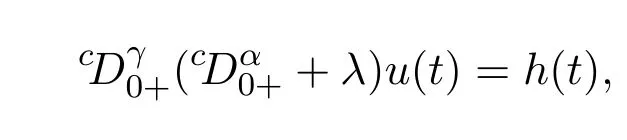
可見u(t)滿足(5).

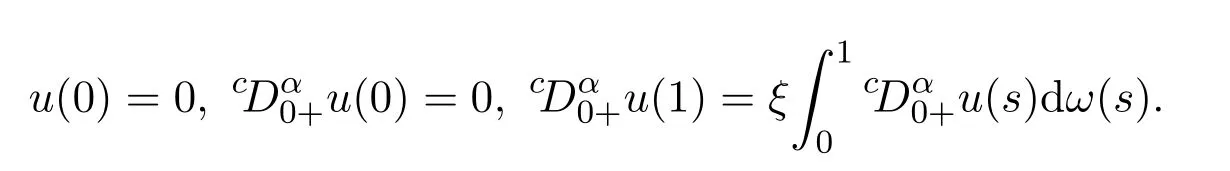
進一步,有故u(t)滿足(4)所以u(t)是問題(3)-(4)的解.證畢.

引理 2 .2設E是一個Banach空間,假設C?E是一個凸閉集.若U是一個相對于C的開子集,其中0∈U并且T:→E是一個全連續映射,T()有界.假設?λ∈(0,1),u∈?U,有 u /=θTU,則 T 在上至少有一個不動點.

3 主要結論

設E=C[0,1]是一個Banach空間,其中范數定義為:

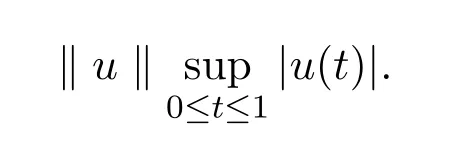
定義映射T:E→E,

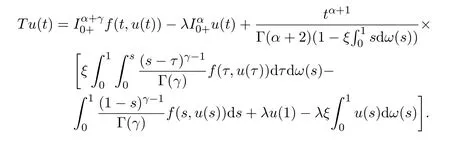
由引理2.2可得,當且僅當T有一個不動點時,u是邊值問題(1)-問題(2)的解.記

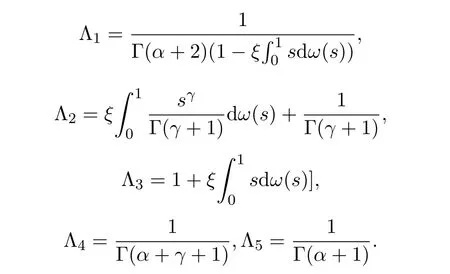
現在我們利用Leray-Schauder非線性抉擇來研究邊值問題(1)-問題(2)的解的存在性.

定理3.1假設滿足以下條件:

(H1)存在一個非負函數ω∈E使得在[0,1]的子集上滿足ω＞0并且有一個不減的函數 φ:[0,∞)→[0,∞)使得 |f(t,u)|≤ω(t)φ(|u|),其中 (t,u)∈[0,1]×R;

(H2)存在M ＞0,使得

則邊值問題(1)-問題(2)至少有一個解.

證明易得T是連續的.下面來證明T是將E上的有界集映射為有界集.對于任意數r＞0,Br={u∈E:‖u‖≤r}是E 上的有界集.則對于u∈Br,t∈[0,1],可得

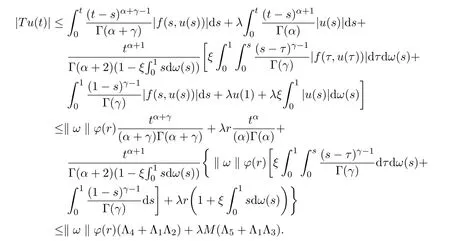
因此

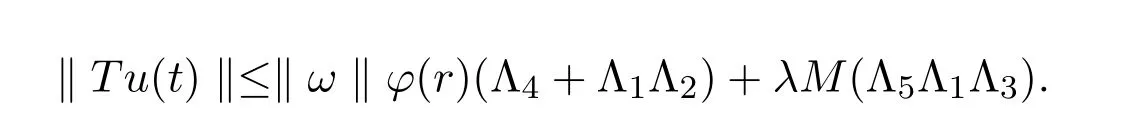
可見TBr有界.

接下來,證明T是將E上的有界集映射為等度連續的集合.對任意t2∈[0,1],其中,t1＜t2,

即知,當 t1→t2時,有

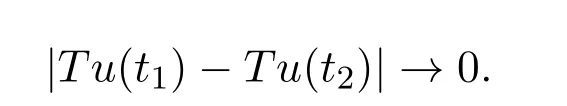
由Arzela-Ascoli定理,可以推導出T:E→E是全連續映射.設θ∈(0,1),u∈E可知u=θTu.由上述類似分析可知,

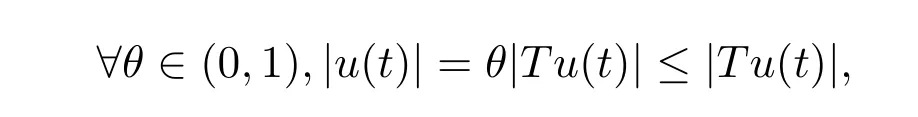
從而

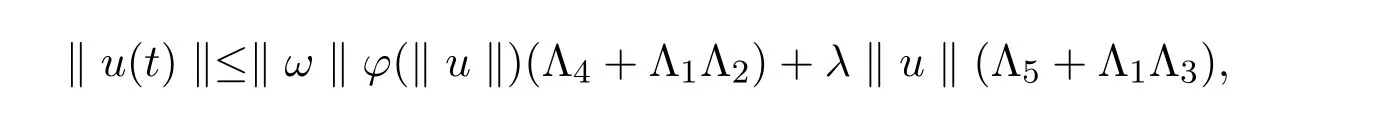
故有

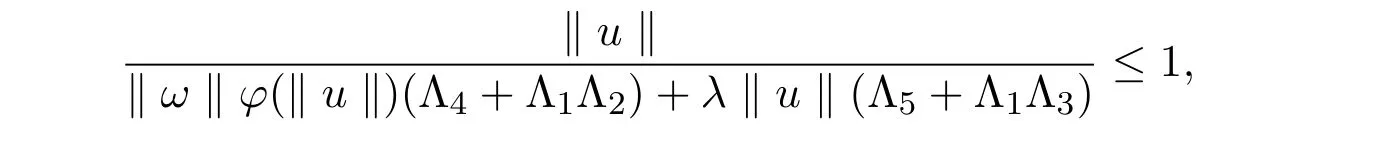
由(H2)以及上式可知,‖u‖/=M,令

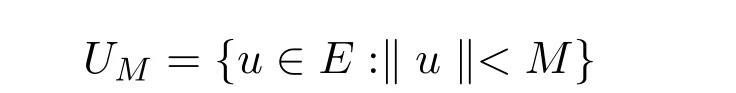
則 ? u∈ ? UM,有 ‖ u‖=M,從而 ? u∈ ? UM,?θ∈ ( 0,1),u/= θ Tu,可知 T :UM→E是全連續映射.因此,引理2.1能確保T至少有一個不動點u∈UM.所以邊值問題(1)-問題(2)至少有一個解.證畢.

定理 3.2假設滿足以下條件:

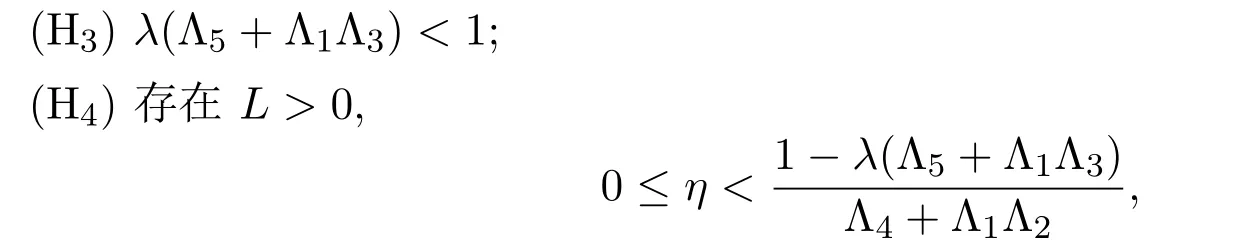
使得

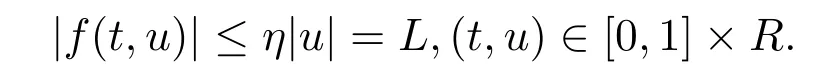
都成立,則邊值問題(1)-問題(2)至少有一個解.

證明考慮算子方程u=Tu.證明T至少有一個不動點u∈E.作

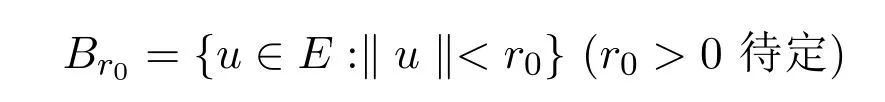
使得

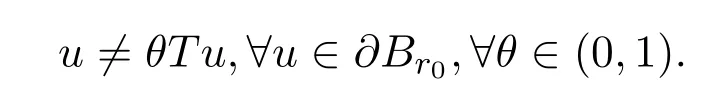
通過定理3.1的證明可知T是全連續的.令

由拓撲度的同倫不變性可知,

其中I定義為單位算子.

利用Leray-Schauder度的非零性,

在Br上至少存在一個解.

假設 u=θTu其中 u∈E,θ∈[0,1].則 ?t∈[0,1],有

得到

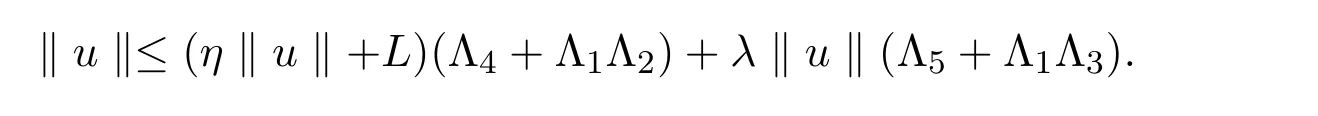
因此

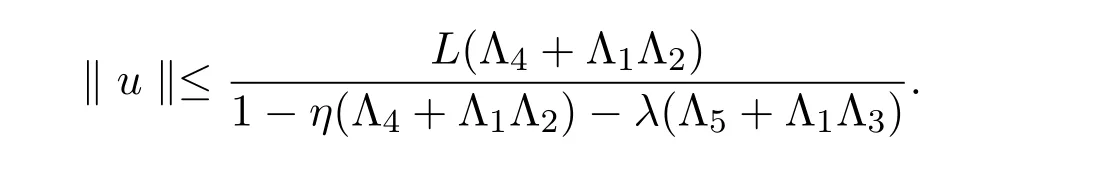
令

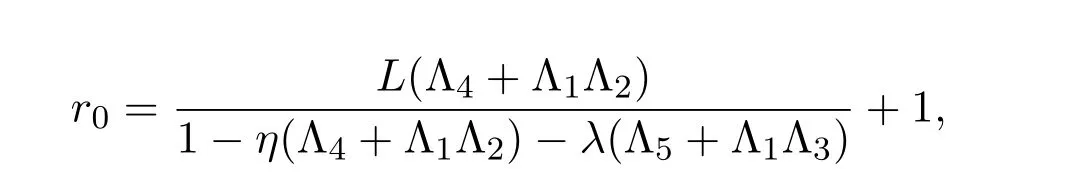
則對任一u∈?Br0有u/=θTu并且θ∈(0,1).因此方程

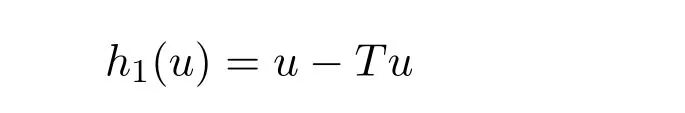
在Br0上至少有一個解.即T在Br上至少存在一個不動點,從而邊值問題(1)-問題(2)至少有一個解.證畢.

4 實例應用

4.1 考慮下列的邊值問題

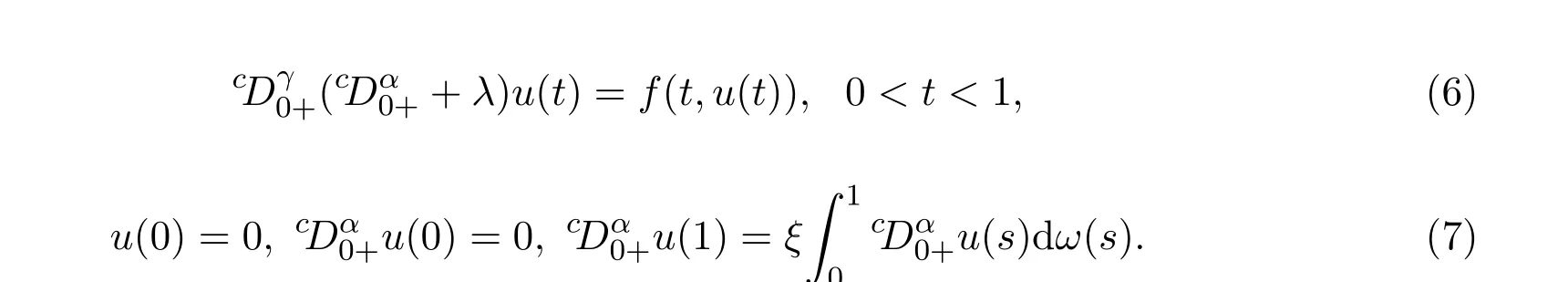
其中

則有

選取

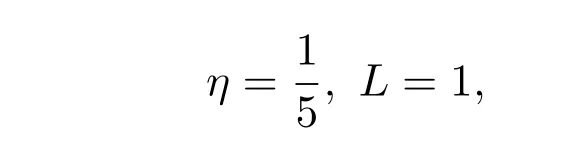
則

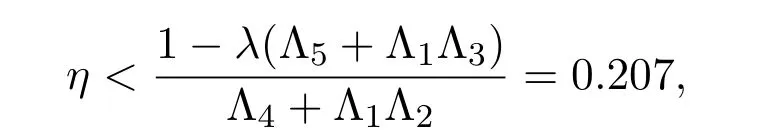
且對 (t,u)∈[0,1]×R有

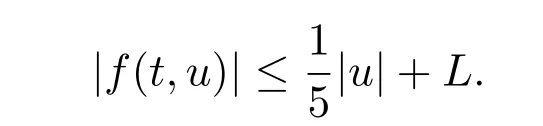
從而定理3.2的條件都滿足,故由定理3.2可知，邊值問題(6)-問題(7)在[0,1]上至少有一個解.

[1]Langevin P.On the theory of Brownian motion[J].Comptes Rendusde Academie Bulgaredes Sciences,1908,146:515-530.

[2]Kubo R.The fuctuation-dissipation theorem[J].Rep.Prog.Phys.,1966,29:255-284.

[3]Burov S,Barkai E.Critical exponent of the fractional Langevin equation[J].Phys.Rev.Lett.,2008,100:590-601.

[4]Li B,Sun S,Li Y.Multi-point boundary value problems for a class of Riemann-Liouville fractional di ff erential equations[J].Adv.Di ff er.Equ.,2014,151:1-11.

[5]Zhang X.Positive solutions for a class of singular fractional di ff erential equation with in?nite-point boundary value conditions[J].Appl.Math.Lett.,2015,39:22-27.

[6]Yu T,Deng K,Luo M.Existence and uniqueness of solutions of initial value problems for nonlinear langevin equation involving two fractional orders[J].Commun.Nonlinear Sci.Numer.Simul,2014,19:1661-1668.

[7]Zhang X,Wang L,Sun Q.Existence of positive solutions for a class of nonlinear fractional di ff erential equations with integral boundary conditions and a parameter[J].Appl.Math.Comput,2014,226:708-718.

[8]Zhang X.Positive solutions for singular higher-order fractional di ff erential equations with nonlocal conditions[J].J.Appl.Math.Comput,2015,49:69-89.

[9]Yukunthorn W,Ntouyas S K,Tariboon J.Nonlinear fractional Caputo-Langevin equation with nonlocal Riemann-Liouville fractional integral conditions[J].Adv.Di ff er.Equ.,2014(3):315-330.

[10]Loghmani G,Javanmardi S.Numerical methods for sequential fractional di ff erential equations for Caputo operator[J].Bull.Malays.Math.Sci.Soc.,2012,35(2):315-323.

[11]Liu Z,Liang J.Multiple solutions of nonlinear boundary value problems for fractional di ff erential equations[J].Bull.Malays.Math.Sci.Soc.,2014,37(1):239-248.

[12]Momani S,Odibat Z.Numerical approach to di ff erential equations of fractional order[J].J.Comput.Appl.Math.,2007,207:96-110.

Existence of solutions for fractional-order Langevin equations with R-S Integral boundary conditions

Wang Xili,Zhou Zongfu
(School of Mathematical Sciences,Anhui University,Hefei230601,China)

In this paper,we investigate a class of boundary value problems of fractional-order Lengevinl equations with R-S Integral boundary conditions.By Leray-Schauder′s nonlinear alternative and Leray-Schauder degree theory,several new existence results of solutions are obtained.An example is given to show the applicability of our main results.

fractional-order Lengevinl equation,integral boundary value conditions,Leray-Schauder′s nonlinear alternative,Leray-Schauder degree theory

O175.8

A

1008-5513(2017)05-0486-10

10.3969/j.issn.1008-5513.2017.05.006

2017-10-12.

國家自然科學基金(11371027);安徽省自然科學基金(1608085MA12).

王西麗(1991-),碩士,研究方向：常微分方程邊值問題.

周宗福(1964-),碩士,教授,研究方向：常微分方程邊值問題.

2010 MSC:34B37,34B15