用洛必達法則巧解函數含參問題

胡意榮

廣東省新興縣第一中學 (527400)

用洛必達法則巧解函數含參問題

胡意榮

廣東省新興縣第一中學 (527400)

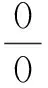
法則一：設函數f(x)、g(x)滿足：

(2)在U°(a)內，f′(x)和g′(x)都存在，且g′(x)≠0；

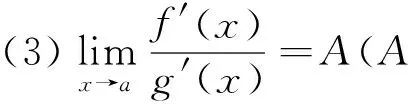
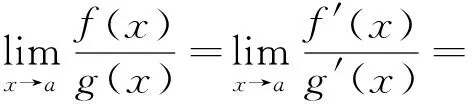
法則二：設函數f(x)、g(x)滿足下列條件：

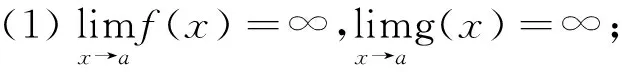
(2)在U°(a)內，f′(x)和g′(x)都存在，且g′(x)≠0；

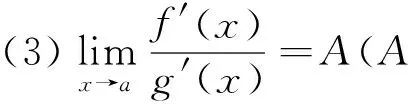
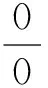
例1 (2016年全國新課標卷2文科第20題)已知函數f(x)=(x+1)lnx-a(x-1).

(Ⅰ)當a=4時，求曲線y=f(x)在(1,f(1))處的切線方程；

(Ⅱ)若當x∈(1,+∞)時，f(x)>0，求a的取值范圍.

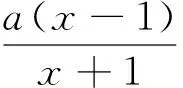
(1)當a≤2，x∈(1,+∞)時，x2+2(1-a)x+1≥x2-2x+1>0，故g′(x)>0,g(x)在(1,+∞)上單調遞增，因此g(x)>0；

(2)當a>2時，令g′(x)=0得

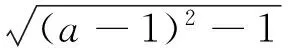
綜上，a的取值范圍是(-∞,2].

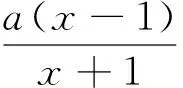
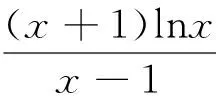
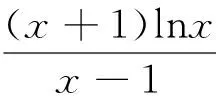
綜上，a的取值范圍是(-∞,2].

點評：通過對比上述兩種解法，不難發現，解法一用的是分類討論的方法，分類時要注意不重不漏，還要簡潔，對解題者的要求較高；而解法二用的是分離參數法，通過分離參數、構造函數，再求導，最后用洛必達法則求極限值，思路清晰，避免了分類討論的麻煩，可以看出洛必達法則在解決此類問題的優越性.

例2 已知函數f(x)=

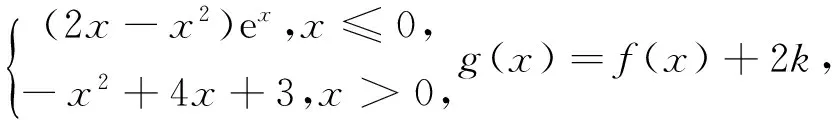
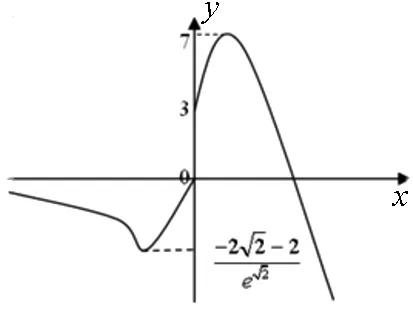
圖1

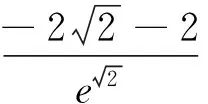
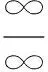
能利用洛必達法則求解參數取值范圍的試題還有很多，這類試題也是近些年來高考中的熱點.下面給出同類型的幾道試題，供讀者練習.

1.(2016年高考數學新課標Ⅰ文科第21題)

已知函數f(x)=(x-2)ex+a(x-1)2.

(Ⅰ)討論f(x)的單調性；

(Ⅱ)若f(x)有兩個零點，求a的取值范圍.

2.(2013年高考數學新課標Ⅰ理科第21題)

已知函數f(x)=x2+ax+b，g(x)=ex(cx+d)，若曲線y=f(x)和曲線y=g(x)都過點P(0，2)，且在點P處有相同的切線y=4x+2.

(Ⅰ)求a，b，c，d的值；

(Ⅱ)若x≥-2時，f(x)≤kg(x)，求k的取值范圍.

3.(2011年高考數學新課標Ⅰ理科第21題)

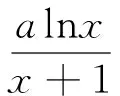
(Ⅰ)求a、b的值；

通過上述這些試題，不難看出，在函數問題中求解參數的取值范圍時，如果能夠分離出參數，把問題轉化為恒成立問題，這時就可以利用導數求解所構造函數的最值，如果最值不存在，只有極限值，那么此時往往可以用到洛必達法則來求解，從而避開分類討論的麻煩，達到提高解題效率的目的.