半空間雙相介質垂直界面裂紋附近圓形襯砌和半圓凹陷對SH波的散射

張希萌， 齊 輝， 項 夢， 丁曉浩

(哈爾濱工程大學 航天與建筑工程學院，哈爾濱 150001)

半空間雙相介質垂直界面裂紋附近圓形襯砌和半圓凹陷對SH波的散射

張希萌， 齊 輝， 項 夢， 丁曉浩

(哈爾濱工程大學 航天與建筑工程學院，哈爾濱 150001)

利用Green函數法、鏡像法與多級坐標法，對半空間中半圓凹陷和圓形襯砌對SH波的散射進行分析，得到其穩態響應。利用鏡像法得到了滿足水平邊界應力自由、垂直邊界位移與應力連續的波函數解析表達式。根據垂直邊界連續性條件,利用“裂紋切割法”和“契合法”建立起求解問題的第一類Fredholm型積分方程，得到了圓形襯砌周邊的動應力集中系數與裂紋尖端動應力強度因子的解析表達式。數值算例分析了入射波數、襯砌深度、半圓凹陷大小、裂紋長度等對動應力集中系數、裂紋尖端動應力強度因子與地表位移的影響,并與已有文獻進行比較。

半空間；圓形襯砌；半圓凹陷；Green函數；動應力集中系數(DSCF)；動應力強度因子(DSIF)

隨著經濟不斷提高，為了緩解交通壓力與維持國計民生，建立了大量生命線工程，例如供水、排水、燃氣、石油管道與地下鐵道工程。很多復雜地形都有如孔洞、凹陷等各種缺陷，含缺陷的地下襯砌結構受到由地震、爆破等彈性波作用后其應力集中問題比靜態時更復雜，生命線工程受損將會導致整個城市或局部社區經濟功能的癱瘓，因此生命線工程在復雜地形中要求有較高的抗震性與安全性，眾多學者對缺陷問題進行研究并取得大量成果。近年來，Qi等[1-4]對直角域或半空間中襯砌與凹陷的動力問題進行了分析，韓峰等[5-6]對多個凸起與凹陷相連地形的動力響應問題給出了數值解，梁建文等[7]研究了地下圓形襯砌的動應力集中問題。孫苗苗[8]分析了空心管樁組成的陣列對SH波的散射問題。

本文利用Green函數法、“鏡像法”與多級坐標法，構造出波函數。根據連續性條件，利用“契合法”與“裂紋切割法”建立第一類Fredholm型積分方程組。分析討論入射角度、入射波數、襯砌埋深、半圓凹陷大小等對動應力集中系數、動應力強度因子與地表位移的影響。

1 問題的描述

如圖1，介質Ⅰ為含半圓缺陷和圓形襯砌的直角域，其質量密度與剪切模量分別為ρ1、μ1， 水平、垂直邊界分別為ΓH、ΓV，半圓缺陷中心位置與垂直邊界ΓV距離為d1， 半徑為c，其邊界為ΓC； 介質Ⅱ為無缺陷的直角域，其質量密度與剪切模量分別為ρ2、μ2； 介質Ⅲ為圓形襯砌，其質量密度與剪切模量分別為ρ3、μ3，中心位置與垂直邊界ΓV距離為d，與水平邊界ΓH距離為h，內、外半徑分別為b、a，內邊界、外邊界分別為ΓB、ΓA； 垂直界面裂紋長度為2A，尖端與水平邊界ΓH距離為h1。本文采用多級坐標展開法，建立坐標系xoy、x1o1y1、x′o′y′，所對應的復坐標系分別為：η=x+yi=reiθ、η1=x1+y1i=r1eiθ1、η′=x′+y′i=r′eiθ′。各坐標系關系為

(1)

本文模型是對半空間中由兩種不同的介質構成的含垂直界面裂紋的復雜地形中凹陷與襯砌在SH波作用下動應力響應這一生命線工程問題的簡化。

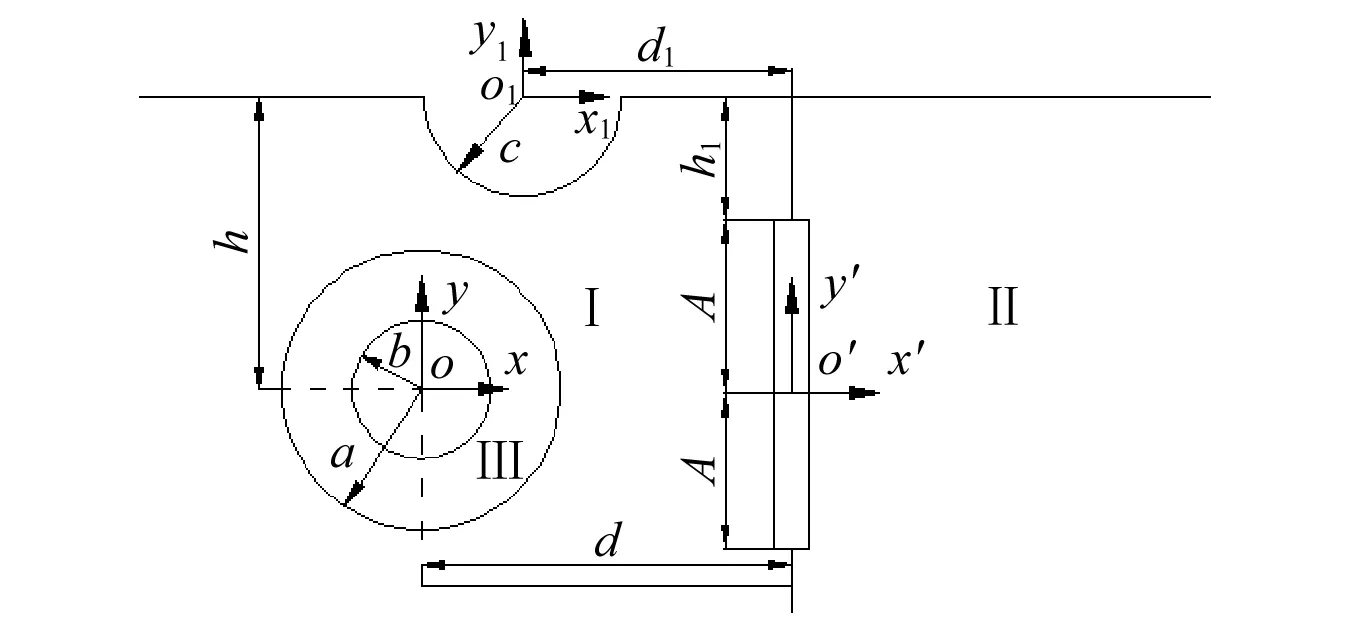
圖1 半空間垂直界面裂紋附近圓形襯砌和半圓形凹陷模型Fig.1 The model of a circular lining and a semi-circular canyon near vertical interface crack in half space

2 Green函數

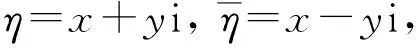
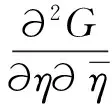
(2)

(3)

本節研究的直角域介質Ⅰ在線源荷載δ(η-η0)作用下的模型如圖2所示。其中η0=d+yi, (y≤h)， 表示η0在垂直邊界ΓV上。

圖2 受線源荷載作用的直角域模型Fig.2 The right-angle plane model impacted by a line source force

介質Ⅰ邊界條件可以表示為

(4)

由線源荷載δ(η-η0)產生并的擾動，可視為已知的入射波Gi，應滿足直角域水平邊界ΓH上應力自由，利用“鏡像法”， 構造出入射波表達式

(5)

對于半圓凹陷形成的散射波Gs1和圓形襯砌所形成的散射波Gs2，均滿足直角域中直線邊界應力自由條件,利用“鏡像法”，構造出其表示式

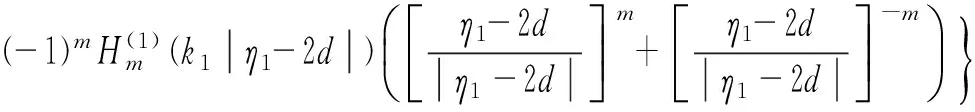
(6)

(7)

式中：

其中：η=x+yi,η1=x1+y1i,η1=η+η0,

η0=(d1-d)-hi,η2=η-2hi,

η3=η-2d,η4=η2-2d

對于介質Ⅲ圓形襯砌內所形成駐波Gst，按文獻[3]中思路，構造其表達式如下：

(8)

由以上推導可知：

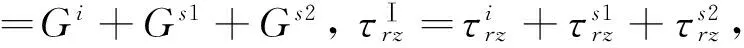
(9)

由邊界條件(3)建立方程組，

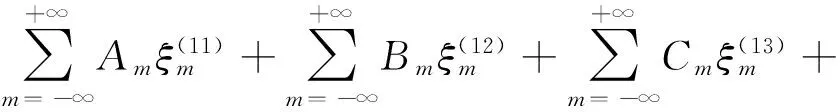
(10)

式中：

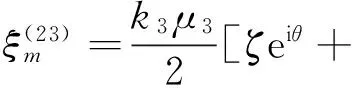
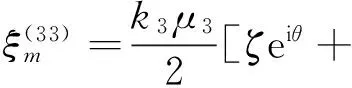
ξ(3)=ξ(4)=0

其中：

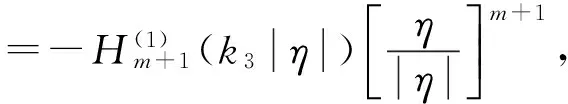
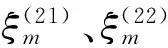
對于介質Ⅱ，其Green函數表達式為

(11)

3 SH波的散射

入射波w(i,e)、散射波w(r,e)和折射波w(f,e)均滿足直角域中水平邊界ΓH上應力自由，垂直邊界ΓV上的連續性條件，按與求解Green函數相同思路，利用“鏡像法”構造其表達：

(12)

(13)

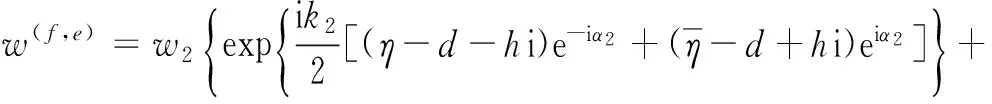
(14)

其中：β0=π-α0,各參數關系式：

k1sinα0=k2sinα2,c1sinα2=c2sinα0

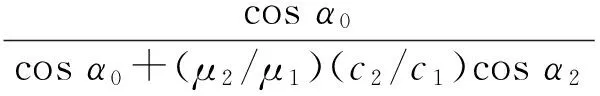
經驗證，式(12)、式(13)、式(14)滿足垂直邊界ΓV連續性條件：

(15)

式中：α0是入射角度；α2是折射角度。在SH波作用下產生的波場與上節中Green函數作用下產生的波場具有相同的形式：

(16)

(17)

(18)

其中未知系數Rm、Tm、Pm、Qm根據邊界條件(4)確定，所列方程組中已知系數與求解Green函數所列方程組中已知系數相同。

4 契 合

在介質Ⅰ中：

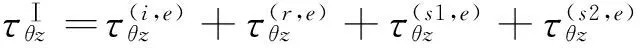
(19)

在介質Ⅱ中：

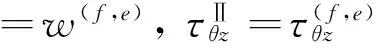
(20)

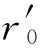
WⅠ+W1+Wc1=WⅡ+W2+Wc2,

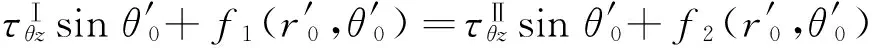
(21)

其中：

(22)

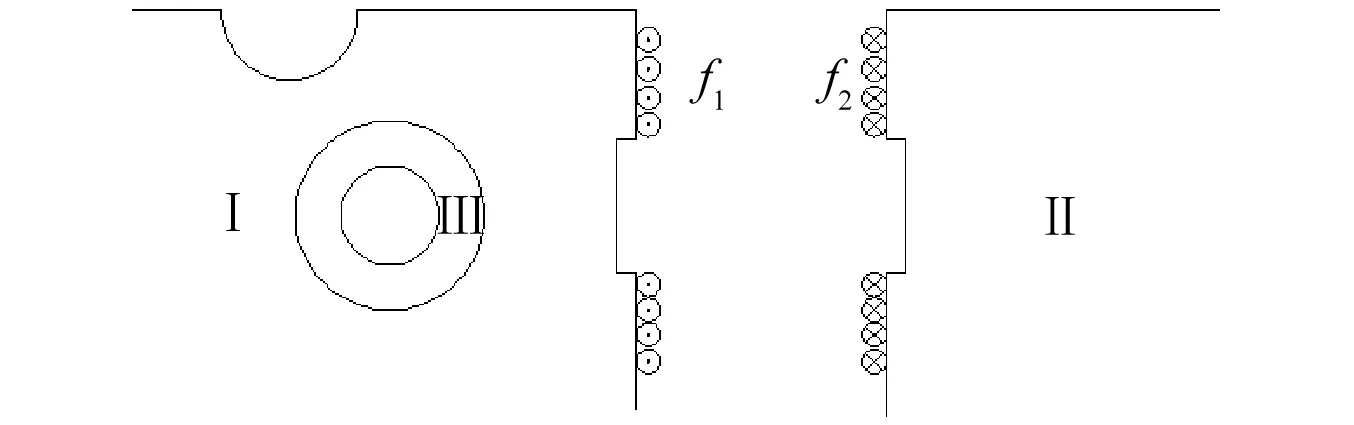
圖3 半空間雙相介質垂直界面的契合Fig.3 Conjunction of vertical interface in bi-material half space

利用式(15)對式(21)進行簡化，得到關于外力系的積分方程：

(23)

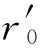
5 動應力集中系數

在SH波作用下環向剪切應力可以表示為

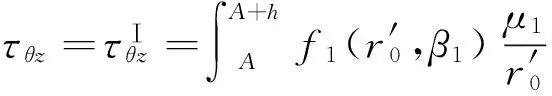
(24)

動應力系數可表示為

6 動應力強度因子

在裂紋尖端外力系f1具有平方根奇異性。引入動應力強度因子

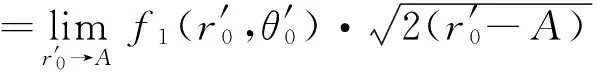
(25)

為在定解積分方程組(18)中直接包含動應力強度因子kⅢ，對被積函數進行變換：

(26)

求解變換后的積分方程組(23)，裂紋尖端對應的值即為動應力強度因子kⅢ。在計算中,通常定義一個無量綱的動應力強度因子k3。

(27)

7 具體算例

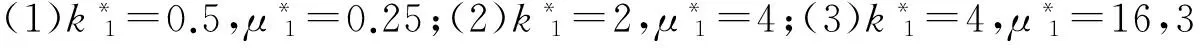
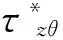
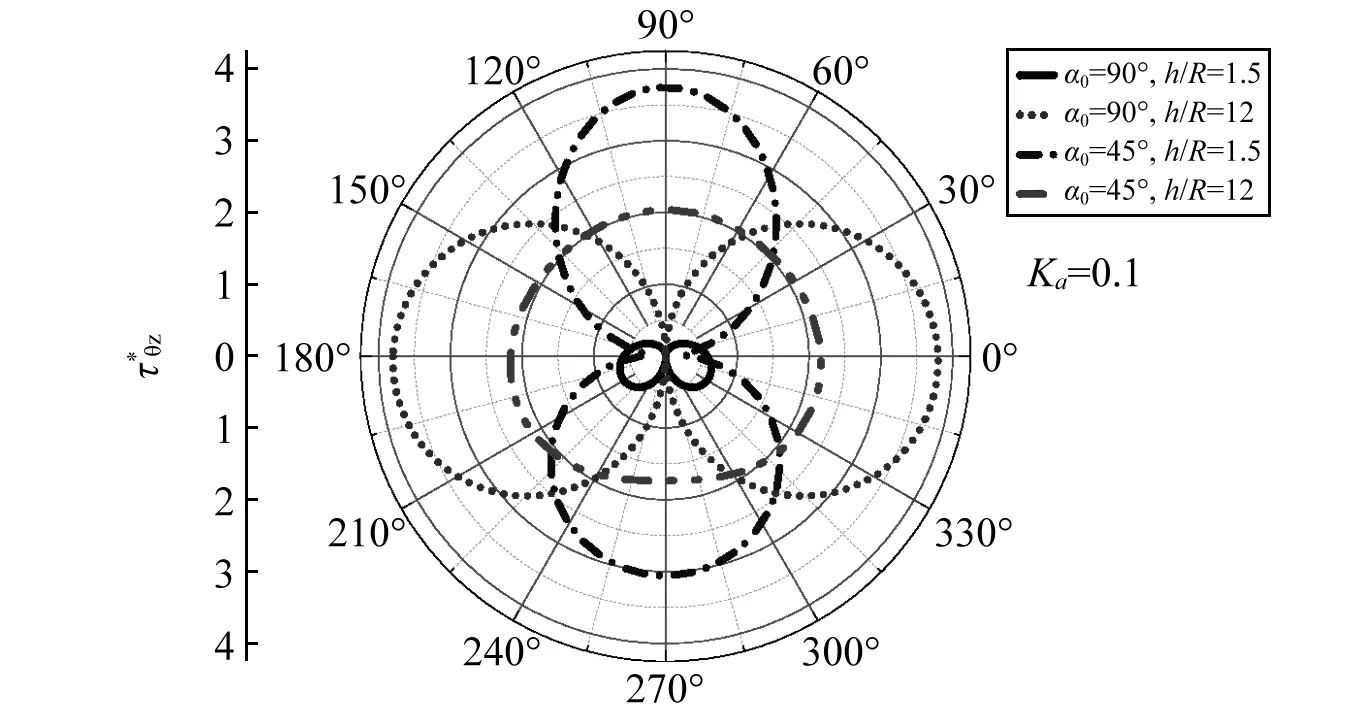
圖4 本文方法的驗證Fig.4 The vertifying of the present method

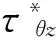
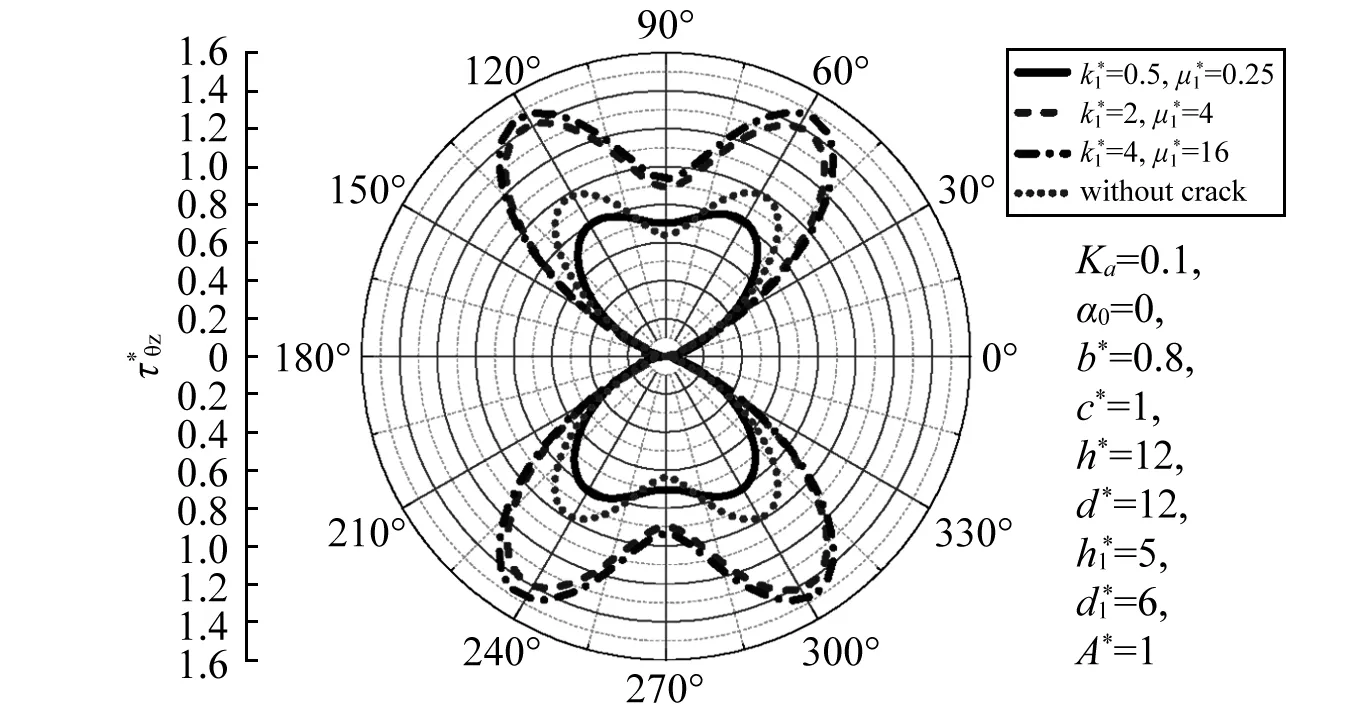
圖5 SH波低頻水平入射時圓形襯砌周邊DSCF隨k*與μ*的分布Fig.5 Distribution of DSCF around circular lining edge vs. k* and μ* by low frequency SH-wave horizontally

(a)

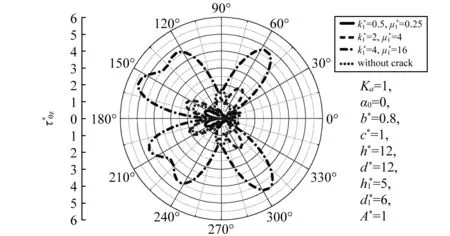
(b)圖6 SH波高頻水平入射時圓形襯砌周邊DSCF隨k*與μ*的分布Fig.6 Distribution of DSCF around circular lining edge vs. k* and μ* by high frequency SH-wave horizontally

圖7 圓形襯砌周邊DSCF隨ka的分布Fig.7 Distribution of DSCF around circular lining edge vs. ka

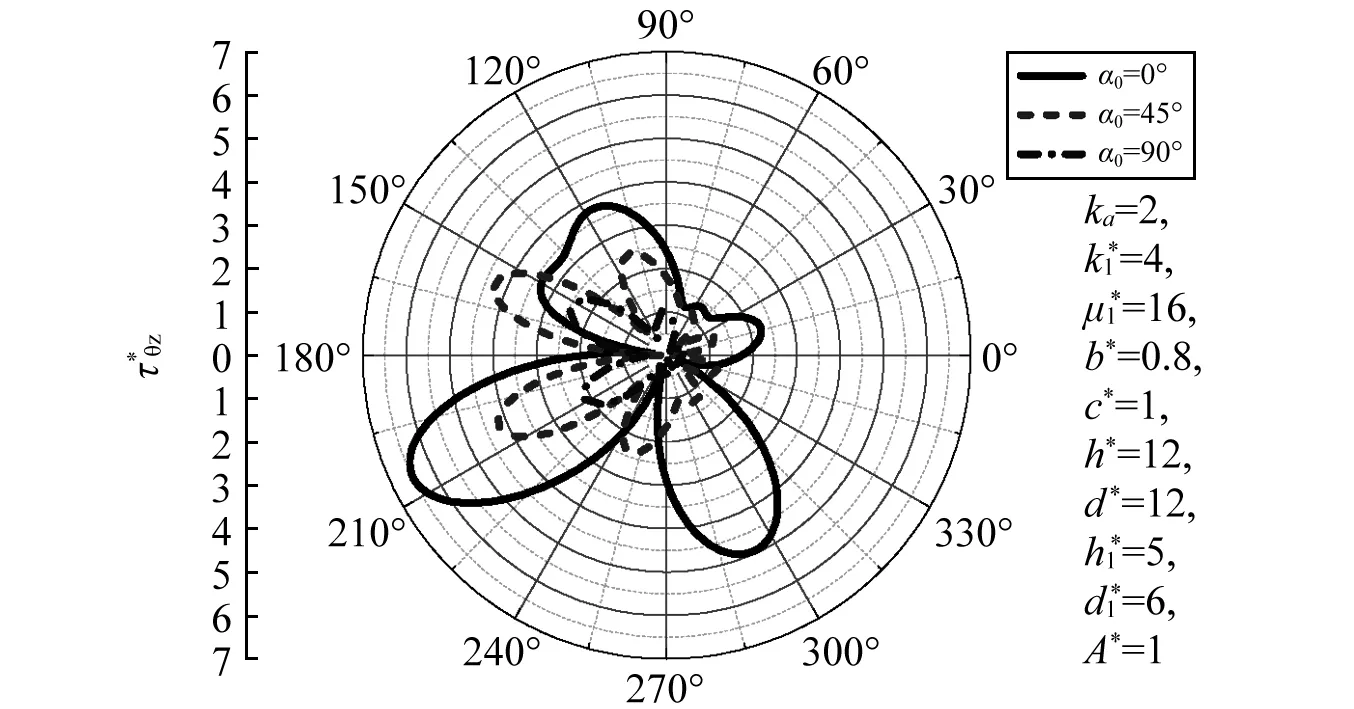
圖8 圓形襯砌周邊DSCF隨α0的分布Fig.8 Distribution of DSCF around circular lining edge vs. α0

由圖5～圖8可知，當SH波高頻水平入射襯砌相對于基體越軟，危害越大。

圖9 圓形襯砌周邊DSCF隨h*的分布Fig.9 Distribution of DSCF around circular lining edge vs. h*

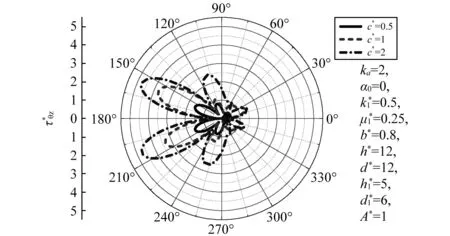
圖10 圓形襯砌周邊DSCF隨c*的分布Fig.10 Distribution of DSCF around circular lining edge vs. c*

圖11 圓形襯砌周邊DSCF隨A*的分布Fig.11 Distribution of DSCF around circular lining edge vs. A*

圖12(b)給出裂紋尖端動應力因子k3隨A*分布情況。由圖12(b)可知，k3呈振蕩變化，A*=2，ka=1.4時k3最大值為9.89， 比A*=0.5，ka=0.6時k3最大值8.08提高了22%。因此裂紋長度A*對k3存在影響。

由以上可知，裂紋長度對裂紋尖端動應力因子k3影響顯著。

圖12 DSIF隨ka的變化Fig.12 Variation of DSIF vs. ka

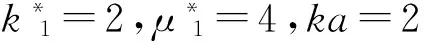
圖13 SH波低頻入射時|W|隨k*與μ*的分布Fig.13 Distribution of |W| vs. k* and μ* by low frequency SH-wave horizontally

(a)

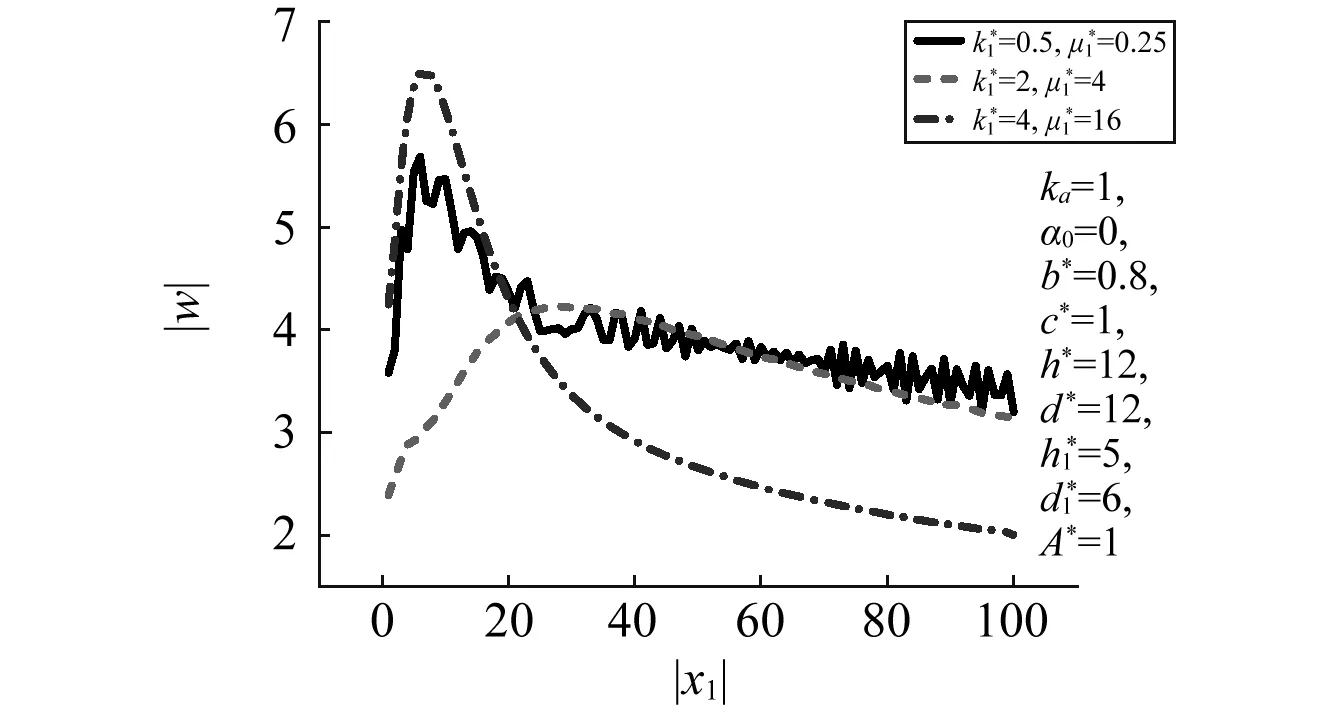
(b)圖14 SH波高頻入射時|W|隨k*與μ*的分布Fig.14 Distribution of |W| vs. k* and μ* by high frequency SH-wave horizontally

圖15給出了地表位移|W|隨ka分布情況。由圖15可知，地表位移|W|受ka影響較大，當x>40時|W|逐漸穩定。當ka=1時，在x=6處|W|達到最大值6.5。

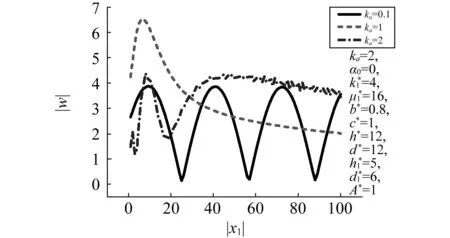
圖15 |W|隨ka的分布Fig.15 Distribution of |W| vs. ka

8 結 論

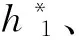
[1] QI Hui, YANG Jie, SHI Yong. Scattering of SH-wave by cylindrical inclusion near interface in bi-material half-space[J].Journal of Mechanics, 2011, 27(1): 37-45.

[2] QI Hui, YANG Jie. Dynamic analysis for circular inclusion of arbitrary positions near interfacial crack impacted by SH-wave in half-space[J]. European Journal of Mechanics /A Solids, 2012, 36: 18-24.

[3] 齊輝, 張根昌, 郭晶. SH波入射半空間雙相介質界面附近圓形襯砌的動力分析[J]. 固體力學學報, 2013, 34(4): 426-432.

QI Hui, ZHANG Genchang, GUO Jing. Dynamic analysis of the scattering of SH waves by circular inclusion near bimaterial interface in half-space[J]. Journal of Solid Mechanics, 2013, 34(4): 426-432.

[4] 齊輝，趙嘉喜，劉殿魁，等. SH 波對脫膠圓夾雜及其邊緣直裂紋的散射[J]. 哈爾濱工程大學學報, 2007, 28(12): 1321-1325.

QI Hui, ZHAO Jiaxi, LIU Diankui, et al. SH waves by cylindrical inclusion and the edge of the horizontal cracks scattering[J]. Journal of Harbin Engineering University, 2007, 28(12): 1321-1325.

[5] 韓峰，王光政，陳翰. SH波對多個凸起與凹陷相連地形的散射問題研究[J]. 應用數學和力學，2013, 34(4): 355-363.

HAN Feng, WANG Guangzheng, CHEN Han. Research on scattering of SH waves on multiple hills and canyons[J]. Applied Mathematics and Mechanics, 2013, 34(4): 355-363.

[6] 許貽燕，韓峰. 平面SH波在相鄰多個半圓形凹陷地形上的散射[J]. 地震工程與工程振動，1992, 12(2): 12-18.

XU Yiyan, HAN Feng. Scattering of SH waves by multiple semi-cylindrical canyons[J]. Journal of Earthquake Engineering and Engineering Viberation, 1992, 12(2): 12-18.

[7] 梁建文,丁美,杜金金. 柱面SH波在地下圓形襯砌洞室周圍散射解析解[J]. 地震工程與工程振動,2013,33(1):1-7.

LIANG Jianwen, DING Mei, DU Jinjin. Diffraction of cylindrical SH waves around circular lined cavity: analytical solution[J].Journal of Earthquake Engineering and Engineering Vibration,2013,33(1): 1-7.

[8] 孫苗苗. 任意排列的空心管樁屏障對SH 波的多重散[J]. 巖土力學, 2014, 35(4): 943-950.

SUN Miaomiao. Multiple scattering of SH waves by rows of arbitrarily arranged tubular piles[J]. Rock and Soil Mechanics, 2014, 35(4): 943-950.

[9] 劉殿魁, 許貽燕. 各項異性介質中SH波與多個半圓形凹陷地形的相互作用[J]. 力學學報, 1993, 25(1): 93-102.

LIU Diankui, XU Yiyan. Interaction of multiple semi-cylindrical canyons by plane SH-waves in anisotropic media[J]. Chinese Journal of Theoretical and Applied Mechanics, 1993, 25(1): 93-102.

[10] 林宏,劉殿魁. 半無限空間中圓形孔洞周圍 SH 波的散射[J]. 地震工程與工程振動,2002, 22(2): 9-16.

LIN Hong, LIU Diankui. Scattering of SH-wave around a circular cavity in half space[J]. Journal of Earthquake Engineering and Engineering Viberation,2002,22(2): 9-16.

[11] 南景富，齊輝，折勇. 垂直半空間界面裂紋及附近圓孔對SH波的散射[J]. 工程力學, 2009, 26(5): 245-256.

NAN Jingfu, QI Hui, SHE Yong. Scattering of SH-wave by interface crack and neighbouring circular cavity in bi-materal vertical half-space[J]. Engineering mechanics, 2009, 26(5): 245-256.

[12] 楊在林，許華南，黑寶平. 半空間橢圓夾雜與裂紋對 SH波的散射[J]. 振動與沖擊，2013, 32(11): 56-61.

YANG Zailin, XU Huanan, HEI Baoping. Interaction of elliptical and crack under incident SH-wave in a half-space[J]. Journal of Vibration and Shock, 2013, 32(11): 56-61.

[13] NAZARET D,LEE V W,LIANG J W. Antiplane deformations around arbitrary-shaped canyons on a wedge-shape half space: moment method solutions[J]. Journal of Earthquake Engineering and Engineering Vibration, 2003,2(2): 281-287.

[14] LIU Diankui, HAN Feng. Scattering of plane SH-waves by cylindrical canyons of arbitrary shapes[J]. Soil Dynamics and Earthquake Engineering, 1991,10(5): 249-255.

[15] 趙博，石永久，江洋，等.一種空間相關多點地震動合成的實用模擬方法[J].津大學學報,2015,48(8): 717-722.

ZHAO Bo, SHI Yongjiu, JIANG Yang, et al. A practical simulation method of spatially correlated earthquake ground motions[J]. Journal of Tianjin University, 2015,48(8): 717-722.

ScatteringofSH-wavebyacircularliningandasemi-circularcanyonnearverticalinterfacecrackinthebi-materialhalfspace

ZHANG Ximeng, QI Hui, XIANG Meng, DING Xiaohao

(College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin 150001, China)

The scattering problem of SH-wave by a circular lining and a semi-circular canyon in the bi-material half space was analyzed by the Green function method, the mirror method and the multi-level coordinate method to obtain the steady state response. The analytical expression of the wave function which satisfies the stress free on the horizontal boundaries, displacement and stress continuity on the vertical boundaries was obtained by the image method. According to the continuity condition on the vertical boundary, the first kind of Fredholm integral equation was set up to obtain analytical expression of dynamic stress concentration factor around the edge of circular lining and dynamic stress intensity factor at crack tip by “the conjunction method” and “the crack-division method”. The influence of the incident wave number, the ground depth of circular lining and the size of semi-circular canyon and the length of crack on the dynamic stress concentration factor, the dynamic stress intensity factor and the displacement along horizontal surface was analyzed and compared with the existed literature through a numerical example.

half space; circular lining; semi-circular canyon; Green function; dynamic stress concentration factor (DSCF); dynamic stress intensity factor (DSIF)

黑龍江省自然科學基金資助項目(A201404)

2016-03-10 修改稿收到日期： 2016-07-21

張希萌 男，博士生，1989年生

齊輝 男，教授，博士生導師，1963 年生

E-mail:qihui205@sina.com

O343.1; O347.3

A

10.13465/j.cnki.jvs.2017.20.022