例談特殊化思想在選擇題求解中的應用

薛日琴

（福清第二中學，福建 福州 350300）

例談特殊化思想在選擇題求解中的應用

薛日琴

（福清第二中學，福建 福州 350300）

選擇題具有靈活多變、知識覆蓋面廣等特點。選擇題的答案包含在四個選項中，往常可以利用特殊化的思想方法求解，選擇題求解時的特殊化思想，包括利用特殊值、特殊圖形、特殊函數、特殊位置等多種方法。

特殊化思想；選擇題；特殊化

在全國高考數學試卷中，選擇題數量多，占分比例高，具有概念性強、量化突出、知識覆蓋面廣、解法多樣化等特點，考生能否迅速、準確、全面、簡潔地求解選擇題，往往是能否取得較好成績的關鍵。

數學選擇題一般是容易題或中難題，壓軸部分有個別難題，當中許多問題的解答可使用特殊方法。解答選擇題，要立足通性通法，也要看到選擇題題型的特殊性，充分利用題干和選擇支兩方面提供的信息，依據題目的具體特點，靈活、巧妙、快速地找到正確選項。

筆者結合教學中積累的部分典型題例，對特殊化思想在選擇題求解中的應用問題進行了思考，總結歸納了以下四種不同的途徑與方法。

一、將字母數值特殊化

對于一些含有變量的問題，往往可以對其賦一些特殊值，以簡化思維過程，達到問題求解的目的。

例1（2017年全國I卷理數第11題）設 x,y,z為正數，且 2x=3y=5z，則

A.2x＜3y＜5z B.5z＜2x＜3y C.3y＜5z＜2x D.3y＜2x＜5z

分析：依常規方法，令2x=3y=5z=k＞1，得

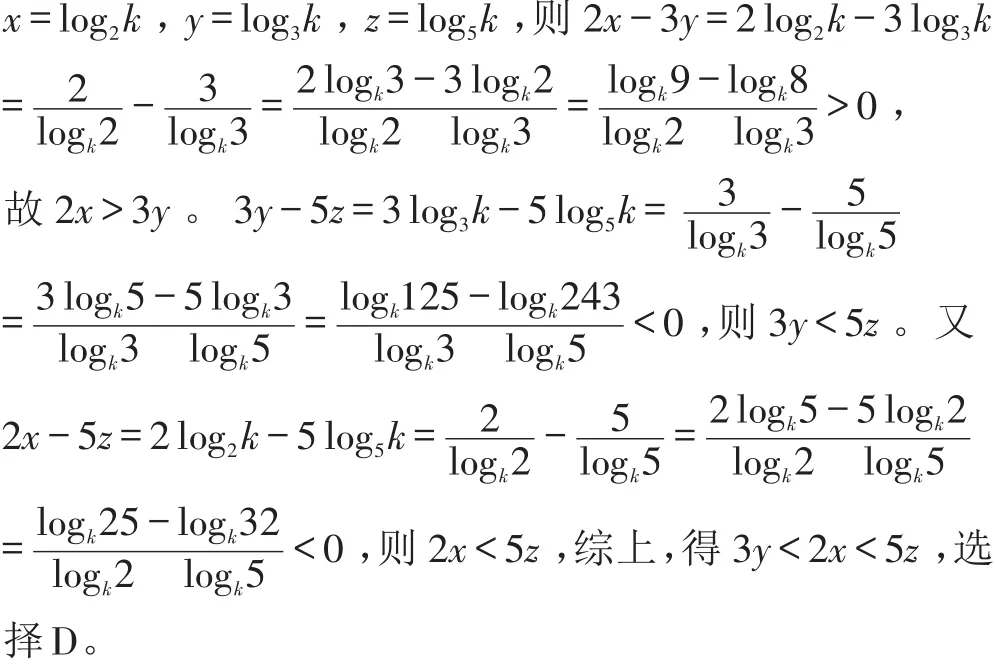
以上解法費時費力，事實上，只需令變量x取特殊值1，本題即可迎刃而解。

解析：令x=1，則3y=5z=2，可得y=log32，z=log52，從而2x=2，3y=3 log32=log38＜2x，5z=5 log52=log532＞2x，從而3y＜2x＜5z，選擇D。

例2（2017年福州市3月質檢理數第9題）已知數列{an}中，a1=1，且對任意的m,n∈N*，都有am+n=am+an+mn ，則

分析：本題考查遞推數列，累加法求數列的通項公式以及裂項相消法求數列的前n項和。對于條件am+n=am+an+mn，很多學生不知道怎么對其進行轉換，導致解題障礙。事實上，通過觀察選項，不需要條件am+n=am+an+mn，亦可求解本題。

二、將圖形狀態特殊化

對于一些問題，如果題設給出的是一般化的圖形，往往可以將其特殊化為特殊圖形進行求解。如條件給出的是一般三角形，往往可以考慮特殊化為直角三角形、等腰三角形、等邊三角形等。如條件給出的是平行四邊形，往往可以考慮特殊化為矩形、菱形、正方形等。

例3（2017年福建省4月質檢理數第9題）已知D,E是ΔABC邊BC的三等分點，點P在線段DE上，若，則xy的取值范圍是

分析：本題條件沒有具體指出ΔABC是什么三角形，故可將其特殊化為等腰直角三角形，以簡化解題過程。

解析：將ΔABC特殊化為等腰直角三角形，不妨設AB=1，可求D,E坐標分別為直線BC的方程為x+y=1。由于點P在線段DE上，D,E是BC的三等分點，故可設點 P坐標為，由，得 到，結合，可知選擇D選項。

例4(2017年福州市5月質檢理數第10題)已知a,b,c分別是ΔABC的內角 A,B,C所對的邊，點 M為ΔABC的重心，若a

分析：本題中的條件“重心”，大部分學生不懂怎么應用，而條件給的更是莫名其妙，學生難以入手。由于題設未限定ΔABC的形狀，故本題可將ΔABC特殊化為特殊的圖形。

解析：對于A選項，不妨設ΔABC是以A為直角，腰長為1的等腰直角三角形，以A為原點，AB所在直線為x軸，建立直角坐標系，可求各點坐標為 A(0,0)、，故可排除A選項。同樣，對于B選項，可構造以C為直角，腰長為1的等腰直角三角形，以將之排除掉。對于C選項，可構造以以頂角，腰長為1的等腰三角形，以線段AB中點為原點，AB所在直線為x軸，建立直角坐標系，求出各點坐標及對應向量，以將之排除掉。對于D選項，構造以以頂角，腰長為1的等腰三角形，以線段AB中點為原點，AB所在直線為x軸，建立直角坐標系，各點坐標為，可知D選項符合題設條件，選擇D。

評注：求解向量問題，往往可以通過向量運算或坐標方法。單純的向量運算，需要尋找各種量之間的相互聯系，思維量比較大。運用坐標方法求解，往往會相應增加運算量，但思維跨度較小，相對更易理解和操作。

三、將抽象函數特殊化

對于一些與抽象函數有關的問題，我們往往可以通過待定系數法構造一些特殊函數，以求解符合題設條件的函數，再利用排除法求解題目，達到化繁為簡的目的。至于構造特殊函數，往往可以從簡單的一次函數、二次函數、反比例函數等入手進行逐個嘗試。

例5（2016年全國甲卷理數第12題）已知函數f(x)(x∈R)滿 足 f(-x)=2-f(x)，若 函 數與y=f(x)圖象的交點為 (x1,y1)，(x2,y2)，… ，(xm,ym)，則

A.0 B.m C.2m D.4m

分析：本題為選擇題的把關題，同樣很多學生卡在了條件 f(-x)=2-f(x)上。事實上，可構造特殊函數來求解此類題。

解析：嘗試令 f(x)=ax+b，由條件 f(-x)=2-f(x)可得 b=1，則 f(x)=ax+1，不妨設 a=1，得 f(x)=x+1。可求函數與y=x+1交點坐標分別為(-1,0)、(1,2)，故 m=2=-1+1+0+2=2。當 m=2選項中能算得2的只有B選項，故選擇B。

例6（2017年龍巖市3月質檢理數第12題）已知函數 f(x)的定義域為R，其圖象關于點(-1,0)中心對稱，其 導 函 數 為 f′(x) ， 當 x＜-1 時 ，(x+1)[f(x)+(x+1)f′(x)]＜0 ，則不等式 xf(x-1)＞f(0)的解集為

A.(1,+∞) B.(-∞,-1)C.(-1,1)D.(-∞,-1)?(1,+∞)

分析：本題同樣為選擇題的把關題，常規方法處理思維跨度大，對于程度中等或中下的學生比較難，下面筆者構造特殊函數法來求解之。

解析：嘗試令 f(x)=ax+b，由于其關于(-1,0)中心對稱，可得 -a+b=0 ，則 f(x)=ax+a ，f′(x)=a ，得(x+1)[ax+a+a(x+1)]=2a(x+1)2，由2a(x+1)2＜0得a＜0，可取 a=-1，從而 f(x)=-x-1，xf(x-1)＞f(0)即x[-(x-1)-1]＞-1，解不等式得-1＜x＜1，故選擇C。

四、將位置關系特殊化

求解選擇題，除了關注題設條件，認真觀察選項之間的差異也很重要，這些差異是問題求解的關鍵，且差異往往“差”在特殊位置，用好它，能收到事半功倍的效果。

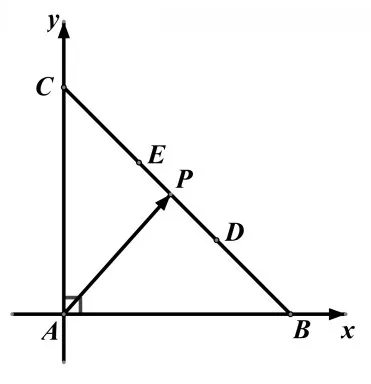
例7（2016年福州高一第二學期期末質檢第11題）如圖，點P是半^徑為1的半圓弧AB上一點，若AP長度為x，則直線AP與半圓弧AB所圍成的圖形的面積S關于x的函數圖象為

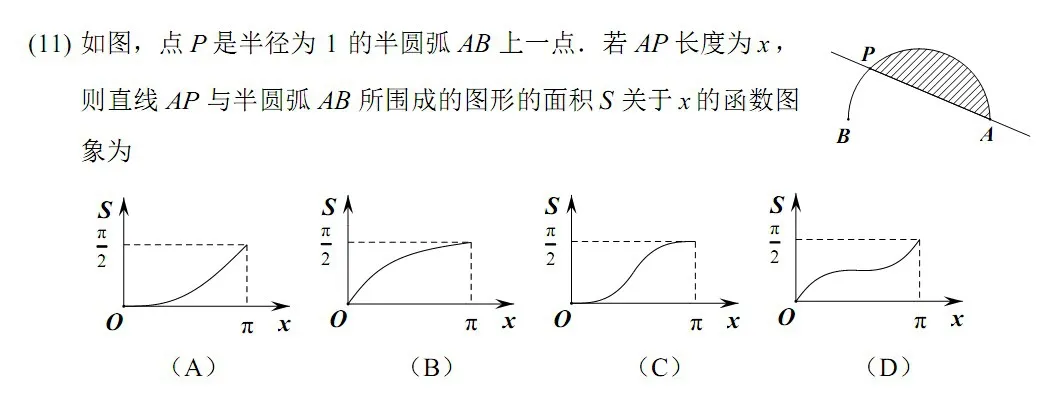
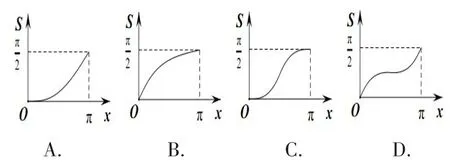
分析：不看選項，直接根據題設條件求S與x的關系，再畫圖求解，顯然這種方法是最不明智的。事實上，觀察4個選項，在這一特殊位置，S的取值存在差異，從這方面入手，結合排除法，即可快速求解本題。

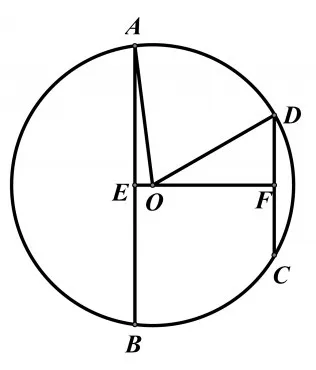
例8（2017年福建省4月質檢理數第10題）空間四邊形ABCD的四個頂點都在同一個球面上，E,F分別是 AB，CD的中點，且EF⊥AB，EF⊥CD。若AB=8，CD=EF=4，則該球的半徑等于

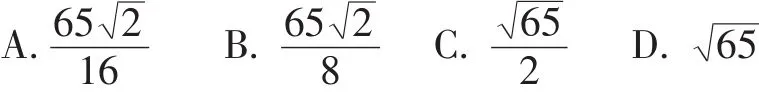
分析：幾何體的外接球問題是常見題型，可是本題的題設條件并不常見，故本題得分率較低。常規方法需要根據條件EF⊥AB，EF⊥CD推導得到球心在EF上，并不易想到，需要學生有較強的空間想象能力。事實上，在保證AB、CD、EF三條線段長度不變的前提下，可將AB繞著E點旋轉，CD繞著F點旋轉，使兩條線段趨向于一個特殊位置，即AB//CD（在這個旋轉過程中，球的半徑總是保持不變），這樣可將空間問題轉化為平面問題進行處理。

解析：考慮AB//CD這種臨界位置，根據對稱，顯然球心O在線段EF上，設OE=x，則OF=4-x，由勾股定 理 得 42+x2=22+(4-x)2，解 得

選擇題的解答思路不外乎直接法和間接法兩大類，直接法是解答選擇題最基本、最常用的方法，如果所有選擇題都用直接法解答，不但時間不允許，甚至有些題目根本無法解答。因此，還要求學生掌握一些特殊的解答選擇題的方法，在平時的練習中有意識地進行應用，反復體味，以提高自己在這方面的能力，達到“多一點想的，少一點算的”的思維訓練。

［1］連佑平.特殊化思想在高中數學解題中的應用［J］.福建教育學院學報，2017（5）.

［2］呂建恒.特殊化思想在解題中的功能［J］.中學數學教學參考，1994（7）.

［3］王新宏.探究特殊與一般思想在高考中的應用［J］.河北理科教學研究，2016（6）.

（責任編輯：王欽敏）