課堂適時提問,提升教學效益
江蘇省海門市六甲初級中學 陸煒鋒
課堂適時提問,提升教學效益
江蘇省海門市六甲初級中學 陸煒鋒
鄭毓信教授提出教師的三項基本功是:善于舉例、善于提問、善于比較與優化。而善于提問作為師生交流最密切的一種方式,在數學教學中起到舉足輕重的作用,因為課堂上的提問是懂的教師向不懂的學生提問,所以這也是教師稚化思維教學的一種表現形式。我們在課堂上要處理好為什么問、問什么、什么時候問的問題。本文基于這三個方面的思考,結合近年來課堂教學的案例,試圖對適時提問(追問)和教學立意做一思考,希望能拋磚引玉。
一、適時提問案例與教學立意解讀
1.指向表現形式
案例1:3000用科學記數法表示為______________。你有什么發現?300000如何用科學記數法表示?
追問1:30萬用科學記數法表示為__________。你能想出兩種表示方法嗎?
追問2:三千萬用科學記數法表示為__________。
追問3:3億用科學記數法表示為__________。
追問4:在我國南海某海域探明可燃冰儲量約有194億立方米,如何用科學記數法表示?你能改變題目,使答案只有一種表示形式嗎?
教學立意:設計的這四個追問,其實都是考查的同一個知識點,就是含文字的數值如何用科學記數法表示,即改變題目的呈現形式,從文字理解上去分析問題,從而得出兩種表示方法,并總結出千、萬、億等數值的科學記數法的規律。讓學生了解到如果既有數值又有文字時,要分析兩種情況,根據問題解答,從而提高了學生分類討論的敏感度和解決問題的嚴謹性。
2.指向自然生成
案例2:已知一次函數y=kx+1的圖象經過點(1,0),則k=___________。
追問1:一次函數y=kx+b的圖象經過點(-2,3)和(1,0),那么這個一次函數的解析式為___________。
追問2:已知一次函數的圖象過點(1,0)與(-2,3),求這個一次函數的解析式。
追問3:根據下表中一次函數的自變量x與函數值y的對應值,可得p的值為( )。

x -2 0 1 y 3 p 0
A.l B. -1 C. 3 D. -3
教學立意:本題是一次函數求解析式的題目,原題很簡單,某些學生口算都能完成。隨后逐問深入,追問1是將一個點變成了兩個點,并讓學生很自然地想到因為要求兩個未知數k和b,所以需要兩個條件;追問2沒有解析式,要讓學生自然而然地想到先設解析式,從而引出待定系數法;追問3既沒有經過的點,也沒有要學生求解析式,但學生會自然地把表格形式變為坐標形式,并設解析式,這種“下套”的方式,學生易于自然生成解答。
最后對于追問3的問題,我又設計了一個問題:如果不求解析式,如何得出p的值?這其實是利用了k的另一種求法,用兩點的縱坐標的差除以它們的橫坐標的差,求解時選擇的數字不一樣,計算的難易程度也不相同,形成了開放式的教學形式和一題多解的理念。
3.指向開放教學
案例3:如圖所示,已知△ABC∽△ADB,且CB=3,AC=4,試求BD的長。
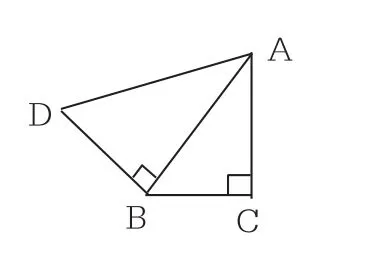
追問1:若把“△ABC∽△ADB”改為“△ABC和△ADB相似”,BD的長是多少?
追問2:求CD的長度。
追問3:你還能改變條件或結論,設計一個新的題目嗎?
教學立意:追問1的意圖就是知道斜邊AD與AB是對應邊,但另外兩條直角邊的對應關系就不明確,故必須分類討論;追問2的意圖則是突然出現求CD的長度,指向“四面八方”,學生無從下手,而實際上還是利用“一線三等角”的模型構造相似三角形,利用勾股定理解題。兩個問題方向不一樣,一個是改變條件,一個是改變求解,既考查了數學的嚴謹性,又考查了數學的開放性。追問3設計了學生編題,指向開放的教和放開的學。
4.指向學科德育
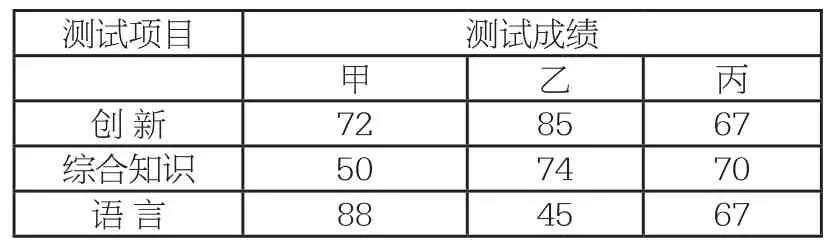
案例4:某廣告公司欲招聘策劃人員一名,對甲、乙、丙三名候選人進行三項素質測試,他們的各項成績如下表所示:
?
(1)如果根據三項測試的平均成績確定錄用人選,那么誰將被錄用?
(2)根據實際需要,若公司將創新、綜合知識和語言三項測試得分按分別占50%、30%和20%的比例確定最終的測試成績,此時誰將被錄用?
追問:若錄用丙,則該如何調整各項測試成績的權?
教學立意:其實丙的成績在前兩種計算中是比較差的,但是設置這樣的一個問題學生就產生了興趣,在學生自主解決后,引導學生思考兩個方面的內容:一是要讓學生建立自信,一個看上去明顯差于別人的人,也會有自己的優點,也能突破極限,二是通過改變權重,將一個看上去能力不行的人成功錄用,有時候在公平性上是說不過去的,這違背了選擇的初衷,要讓學生知道其實加權平均數是一把“雙刃劍”,要用好“這把劍”,不管是現在還是以后走上社會,都要做一個有底線的人。
二、寫在最后
章建躍教授說:保證課堂教學質量和效益的兩個關鍵是“自然的過程”和“恰時恰點的問題”。所以對于課堂中的提問,有課前對學材的再建構,也有課堂上由學生引發的新的追問,如何才能恰時恰點地提出問題而又不顯得突兀,這是一個需要教師長期實踐和反思的問題。上面的四個案例只是管中窺豹,其實每堂課都有追問,都有對話,而如何深度地進行對話需要我們大家一起行動起來。
【備注:本文系江蘇省教育科學十三五初中重點資助課題《初中數學“學材再建構”研究》(課題編號:E-a/2016/06;主持人:施俊進、徐強)主要研究成果之一。】

