一種快速重頻參差信號分選方法

劉正成，齊永梅，姚志均

(中國船舶重工集團公司第七二三研究所，江蘇 揚州 225001)

一種快速重頻參差信號分選方法

劉正成，齊永梅，姚志均

(中國船舶重工集團公司第七二三研究所，江蘇 揚州 225001)

針對重頻參差信號的分選，提出了一種快速信號分選方法，首先對參差信號脈沖序列的到達時間(TOA)做一次一階差分運算，然后提取出所有滿足條件的脈沖重復間隔(PRI)值，同時得到該參差信號的相周期、幀周期和參差數；最后，對脈沖序列的TOA做一次或多次高階差分運算，并利用之前獲得的相周期和參差數，解出各相周期的順序關系。仿真實驗結果表明，本文提出的方法在脈沖丟失率達到40%時仍能正確分選，且計算速度快。

雷達信號分選；脈沖重復間隔；參差信號；差值直方圖

0 引 言

雷達信號分選是電子支援措施(ESM)和電子情報(ELINT)的關鍵組成部分，是指從接收機截獲到的密集雷達脈沖流中分離出屬于各部雷達的脈沖串，其實質就是對脈沖序列進行去交疊、去交錯處理。在密集的電磁信號環境中，一般利用脈沖的瞬時參數，如載頻(RF)、到達方向(DOA)、脈寬(PW)和脈沖幅度(PA)等進行預分選，可以起到稀釋信號密度的作用；然后利用脈沖的到達時間(TOA)進行主分選，也稱重頻分選，主要是通過估計各部雷達的脈沖重復間隔(PRI)，并根據PRI抽取脈沖實現分選目的。

目前雷達偵察系統中常用的基于PRI的分選算法有自相關函數法[1]、累積差值直方圖法(CDIF)[2]、序列差值直方圖法(SDIF)[3]和PRI變換法[4-5]。Mardia等人[2]對PRI分選進行了深入研究，在傳統直方圖分析方法的基礎上結合序列檢索算法，提出了累積差直方圖算法，該算法對于干擾脈沖和脈沖丟失不敏感，但當PRI具有隨機抖動變化時，無法正確分選，而且CDIF需要計算很大的差值級數，當脈沖丟失時，會出現子諧波。之后，Milojevic等人[3]對CDIF算法進行改進，提出了序列差直方圖算法，解決了CDIF算法中計算量大的問題，取消了2倍脈沖間隔的直方圖值與門限比較，從而節約了一半時間，但SDIF法仍然存在與CDIF法一樣致命的缺點，即當PRI具有隨機抖動特征時，無法正確分選，且無法抑制諧波的出現。為此，Nelson等人[4]提出了PRI變換法，該方法在計算自相關時增加了一個相位因子以抑制子諧波，隨后Nishiguchi等人[5]對PRI變換法做了改進，采用可變的時間起點和交疊的PRI箱技術以解決因抖動引起的相位誤差增大問題，從而實現對重頻抖動信號的分選。

CDIF、SDIF、PRI變換這3種方法都是針對重頻固定或重頻抖動的雷達信號的，當用于重頻參差信號分選時，理想情況下，即沒有脈沖丟失時，根據脈沖序列的到達時間進行一級差值直方圖計算，然后對直方圖結果進行統計，統計峰值個數，將各峰值之間的差值在規定的容差范圍內的值提取出來，進行地址對確認，還能正確分選，但當脈沖密度大、參差數多、脈沖丟失率高的情況下，它們就失效了。為此，本文提出了一種在脈沖丟失率很高時仍能正確分選的新方法，且該方法沒有參數需要設置，計算量小。

1 重頻參差信號的脈沖序列模型

重頻參差信號的數學模型[6]如下：

(1)

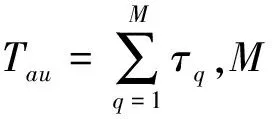
圖1給出了一個6參差的重頻參差脈沖序列示意圖。重頻參差信號具有一定的反偵察能力，因為具有不同的重頻，使得在距離和速度上不易產生模糊。通常情況下，最大參差比被限制在1.5～2.0之間[7]，也就是說最大相周期不大于2倍的最小相周期。

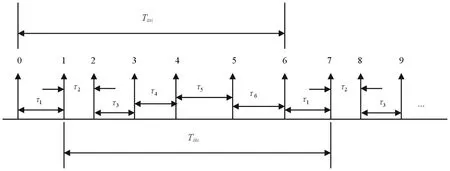
圖1 參差信號PRI

2 本文提出的信號分選新方法

上一節已提到，一般情況下參差信號的最大參差比不超過2，根據這一約束條件，本文提出了一種快速重頻參差信號分選新方法。本方法主要分兩大步：第1步，利用TOA信息估計幀周期、相周期及參差數；第2步，解算各相周期之間的順序關系。新方法的詳細步驟如下：

(1) 對于一個含有N個脈沖的參差脈沖序列，對其到達時間tTOA(i)，i=0,1,…,N-1做一次一階差分運算，得到一個關于PRI信息的向量D1，其計算公式為：

D1(i)=tTOA(i+1)-tTOA(i),0≤i≤N-2

(2)

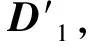
(3)

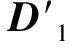
(4)

(3) 對脈沖序列的TOA做一次M階差分運算，得到向量DM，然后判斷向量DM中是否有等于幀周期Tau的值。若有，任選一個值為幀周期的索引號i，并對從i到i+M的TOA做一次一階差分運算，得到各相周期之間的順序關系：τ1,τ2,…,τM；若沒有，則令m=M-1，并轉(4)。

(4) 對脈沖序列的TOA做一次m階差分運算，得到向量Dm，然后判斷向量Dm中是否有等于幀周期Tau的值。若有，設向量Dm中共有l個元素的值等于幀周期Tau，它們的索引號向量Ind為:

Ind={i|Dm(i)=Tau}

(5)

(5) 根據這些索引號從TOA中提取數據，得到一個l×(m+1)維矩陣C，其每一行元素為：

C(j,:)=tTOA(Ind(j):Ind(j)+m)

(6)

(6) 對矩陣C中的每一行做一次差分運算，得到的仍是一個矩陣，然后該矩陣中可能存在元素相同的行，故對其做去重復處理，最終得到一個r×m維矩陣T。

(7) 因為存在脈沖丟失，故矩陣T往往存在多行數據，即有r>1，此時可以結合估計得到的{τq}q∈{1,…,M}解出各相周期的順序關系：τ1,τ2,…,τM；若此時的矩陣T只有一行，即r=1，則令m=m-1，并重復步驟(4)～(7)，直至解出各相周期的順序關系為止。

3 仿真驗證

3.1 有效性驗證

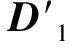
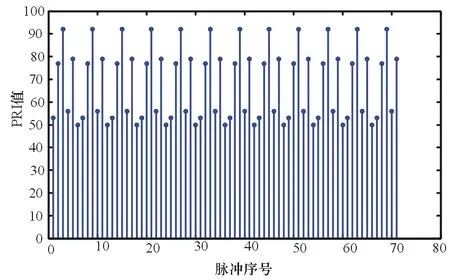
圖2 無脈沖丟失情況下的參差脈沖序列各參差時序圖

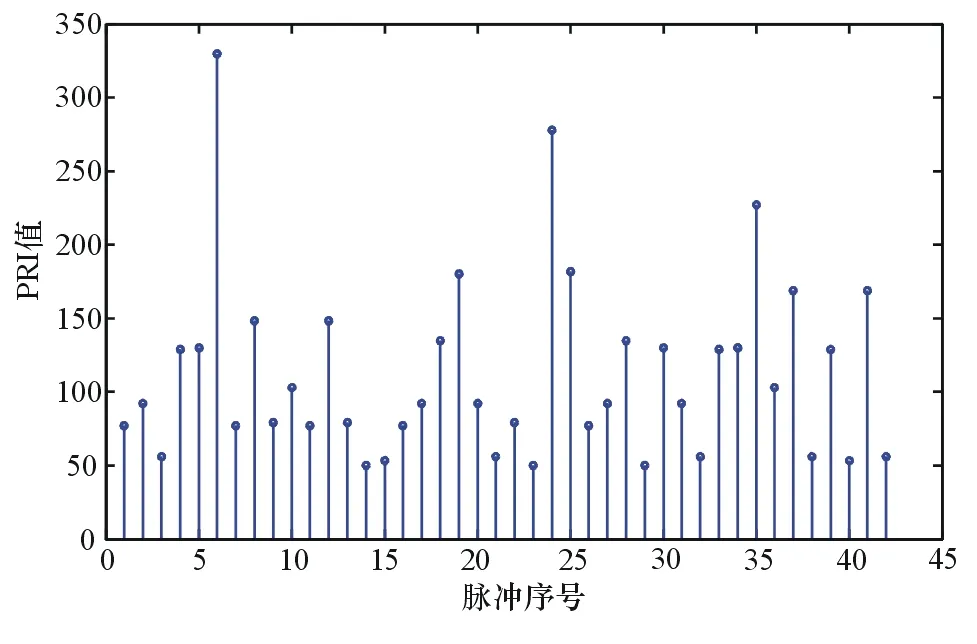
圖3 有脈沖丟失情況下實際檢測到的各脈沖PRI值

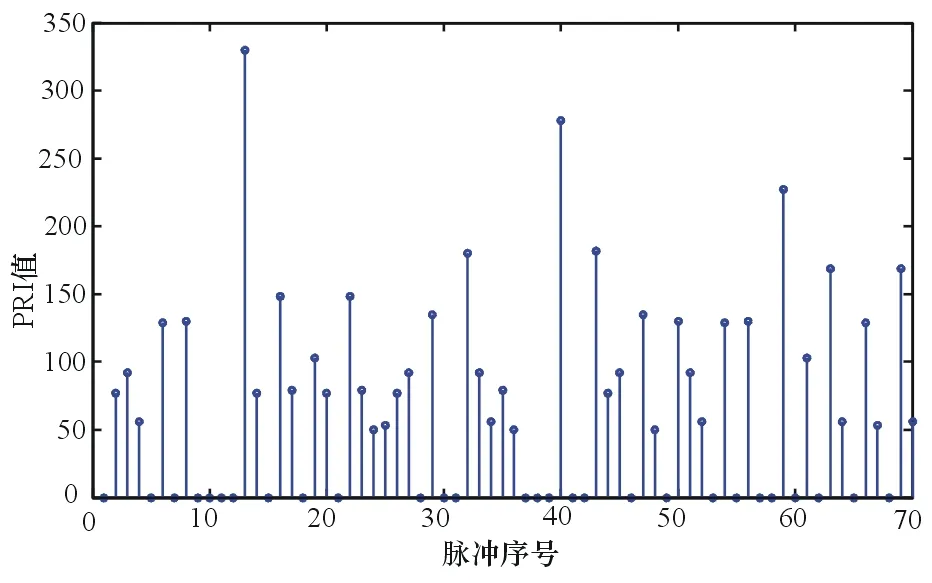
圖4 將圖3中的脈沖對應到圖2中的效果圖

圖5 對參差脈沖序列的TOA做一次一階差分運算所得的向量

獲得相周期和參差數后，接下來就解算各相周期之間的順序關系。圖6是對脈沖序列的TOA做一次6階差分運算后得到的向量D6。從圖6中可以看出,沒有一個元素的值是等于407的，于是對脈沖序列的TOA做一次5階差分運算后得到向量D5，如圖7所示。從圖7可以看出，有3個元素的值是等于407的，它們的索引號分別為11、12和14，然后根據步驟(5)和(6)得到關于相周期順序關系信息的矩陣T，如圖8所示。圖8表示1個幀周期內脈沖數為5個，即表示5個相周期，實際估計得到的相周期個數為6個，它們的集合EstimatedTAU為：{50,53,56,77,79,92}。取矩陣T中的第1行，并與估計得到的參差集合EstimatedTAU作比較，發現第1行中多了一個“148”，但少了2個值：“92”和“56”。可以發現，第1行中多出來的這個“148”剛好等于少的這2個PRI值之和，于是可以肯定“56”和“92”應該位于“148”這個位置，至于兩者的前后關系待定，而其他4個相周期的順序關系已定。接著觀察矩陣T的第2行，看該行中是否出現“56”或“92”，只要出現其中一個，則它們兩者的順序就可以確定下來，而事實上該行中出現了“92”，而“92”之前的值為“77”，故“56”應該在“92”之后，于是該脈沖序列各相周期的順序關系為：77、92、56、79、50、53，與實際的順序關系一致。

圖6 對脈沖序列的TOA做一次6階差分運算后得到的向量D6

圖7 對脈沖序列的TOA做一次5階差分運算后得到的向量D5

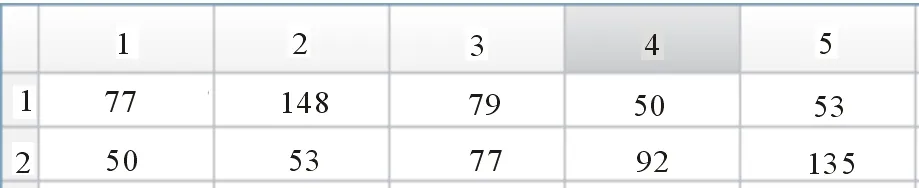
圖8 根據步驟(5)和(6)所得的矩陣T

3.2 快速性驗證

為了驗證本文方法的快速性，進行本文方法與CDIF算法的計算耗時對比試驗，即針對不同參差數的參差信號，比較2種方法的耗時。參差信號的參差數取值范圍為4～8，對于每一種參差數，都測試50次，然后取平均值，統計結果如表1。注，在脈沖丟失率高時，CIDF算法無法解算各相周期之間的順序關系，故這里CDIF算法的耗時只算它正確估計出幀周期所耗的時間，而本文方法的耗時是指估計出正確的幀周期、相周期、參差數及各相周期之間的順序關系所耗時間。從表1可以看出，本文方法比CDIF算法快。

4 結束語

當重頻參差信號脈沖序列中的脈沖丟失率比較高時，傳統的基于PRI的CDIF或SDIF最多只能估計出幀周期和參差數，但無法解算各相周期及它們之間的順序關系。為此，本文提出了一種快速信號分選方法。該方法首先對TOA進行一級差值計算，然后根據參差比約束條件得到相周期、參差數和幀周期，接著再對TOA進行多級差值計算，并結合已獲得的相周期和參差數解算出各相周期的順序關系。實驗結果表明，在脈沖丟失率高達40%的情況下，本文方法仍能正確估計出幀周期、參差數、相周期及它們之間的順序關系；此外，與CDIF相比，計算耗時小很多(如表1所示)，且無需設置任何參數。

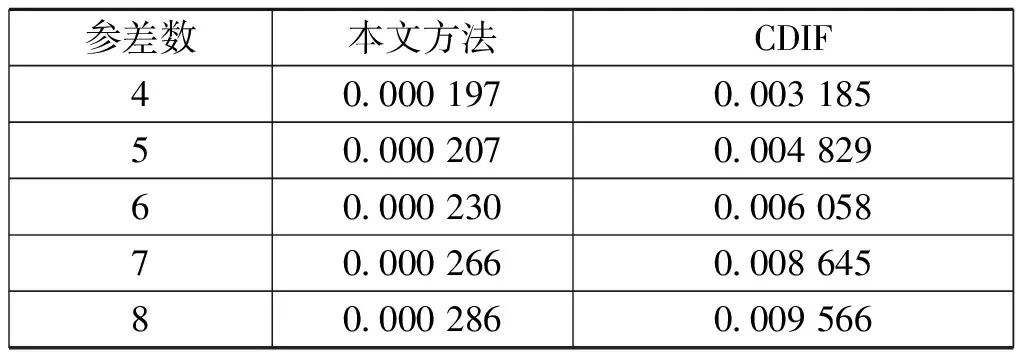
表1 本文方法與CDIF算法計算耗時對比(單位：s)

[1] 趙健生.艦載干擾機信號分選的分類處理方法[J].船舶工程，1995(2):45-49．

[2] MARDIA H K.New techniques for the deinterleaving of repetitive sequences[J].IEEE Proceedings,1989,136(4):149-154.

[3] ILOJEVIC D J,POPOVIC B M.Improved algorgithm for the deinterleaving of radar pulse[J].IEEE Proceeding,1992,139(1)：98-104.

[4] NELSON D J.Special purpose correlation functions for improved signal detection and prameter estimation[C]//Proceedings of International Conference on Acoustics,Speech,and Signal Processing (ICASSP),1993:73-76.

[5] KENICHI N,MASACKI K.Improved algorithm for estimating pulse repetition intervals[J].IEEE Transactions on Aerospace and Electronic Systems,2000,36(2):407-421.

[6] 趙國慶.雷達對抗原理[M].西安:西安電子科技大學出版社,1999.

[7] 丁鷺飛,耿富錄.雷達原理(修訂版)[M].西安:西安電子科技大學出版社,1980.

SortingMethodofAFastPRFStaggeredSignal

LIU Zheng-cheng,QI Yong-mei,YAO Zhi-jun

(The 723 Institute of CSIC,Yangzhou 225001,China)

This paper proposes a fast signal sorting method for the sorting of pulse reqetition interval (PRF) staggered signal,firstly uses the proposed method to calculate the first-order differential values of the time of arrival (TOA) for staggered signal pulse sequence;then extracts all PRI values to meet the conditions;obtains the phase cycle,frame period and the number of stagger PRIs of the staggered signal;finally makes one or more high order differential operations on the TOA of staggered pulse signal sequence,and solves the order relationship of all phase cycles by using the obtained phase cycles and the number of stagger PRIs.The simulation results show that the proposed method still correctly sort the staggered signal sequence when the pulse loss rate reaches 40%,and the computing speed is fast.

radar signal sorting;pulse repetition interval;stagger signal;difference histogram

TN971.1

A

CN32-1413(2017)05-0070-04

10.16426/j.cnki.jcdzdk.2017.05.015

2017-08-30