利率市場化進程、商品價格變動及貨幣政策效應

(深圳大學經濟學院，廣東 深圳 518060)

引言

近年來全球經濟環境復雜多變，大宗商品的價格走勢波詭云譎。大宗商品位于經濟產業鏈條的上游，在經濟體系中處在特殊位置，對整體物價水平的形成發揮重要作用。貨幣當局運用各項政策工具調節貨幣供應量，影響社會總需求，是驅動商品價格變動的重要因素。隨著利率市場化逐步深入和商品金融化日益突出，貨幣政策對商品價格的影響機制趨于復雜。

貨幣政策工具有數量型和價格型。數量型貨幣政策框架，主要通過調整法定存款準備金率、公開市場操作、直接信貸規模控制等工具調節貨幣供給規模。寬松的貨幣環境導致更充沛的市場流動性，為商品價格注入上漲動力，而流動性緊縮則可能驅使商品價格下跌。近年來，貨幣政策框架從數量型向價格型轉軌呼聲漸高，學界廣泛認為應逐步形成利率走廊，更好地發揮利率的自動穩定器調節功能。實際上，我國利率市場化已經取得階段性成果，利率對大宗商品價格的影響渠道正在形成，但影響機制尚未理清。本文試圖剖析商品價格對市場利率所蘊含市場信息的反應模式，籍此探討貨幣政策沖擊在商品市場的傳導機制，為貨幣政策實踐觀察提供理論視角。

研究視角主要投向商品價格變動中隱含的利率過程，將其視為市場利率在商品市場的反應，以此為框架研究利率在商品市場的影響機理。一般地，市場無風險利率作為持有庫存的資金占用成本，以貼現因子形式出現在商品期貨定價之中，但風險中性定價中的無風險利率假設是建立在貨幣市場運行機制相對完善且市場信息傳導機制相對健全的基礎上。鑒于我國金融市場尚未成熟，貨幣市場發展相對滯后，商品市場有時存在貿易融資套利現象，市場利率在商品市場的傳導機制可能并非如庫存理論所描述的。因此，本文假設，經由商品期貨市場吸收所表現出來的隱含利率受到真實市場利率影響，其動態過程的長期均衡水平和波動率均為真實市場利率的函數；并將假設嵌入到Liu and Tang(2011)[13]的期貨定價模型中；最后，借助期貨市場數據進行實證觀察商品期貨市場的利率信息反應機制。

文獻綜述

關于市場利率如何影響商品價格的討論，主要依據Brennan(1958)[3]提出的庫存理論，該理論認為市場利率是持有商品庫存所形成邊際成本中的資金占用成本部分，較高的市場利率會增加持有庫存的資金成本并降低庫存需求，從而促進商品現貨供給，壓低商品現貨價格。

Kitchen and Denbaly(1987)[12]、Fama and French(1987)[8]、Pindyck(2001)[14]等對庫存理論進行實證檢驗并獲得支持性依據。Frankel(1986)[9]的超調模型對研究市場利率與商品價格關系提供了理論框架，其借鑒匯率超調理論，在商品市場提出了價格存在粘性條件下的商品價格“超調”現象，為解釋商品價格對貨幣政策沖擊的響應模式提供基礎理論框架。此外，Barsky and Kilian(2004)[2]在分析20世紀70年代以來石油價格行為時指出，高油價并非外生于宏觀經濟環境，而是寬松貨幣政策導致的結果。Akram(2009)[1]表明大幅上漲的商品價格有可能是受到寬松的貨幣政策的推動。在該理論觀點指引下，諸多學者就市場利率對商品價格影響進行了實證研究，如Scrimgeour(2015)[18]發現市場利率突然變化10個基點會引起商品價格下降0.5%，而且各種商品價格對貨幣政策沖擊的反應有所差異，尤其有色金屬相對于農產品反應更為劇烈；Wang and Hu(2015)[19]運用MF-DXA方法觀察市場利率和農產品價格的交叉相關關系，并且發現交叉相關關系具有時變特征并依賴于商品種類。

關于商品期貨價格行為，現有豐富研究文獻，例如，危慧惠、樊承林和朱新蓉(2012)[25]、何志剛和劉迪(2012)[23]、安毅和宮雨(2014)[21]、鄭尊信等(2014)[31]、張蜀林和何曉燕(2015)[27]、張學文和孫文松(2015)[28]，等等。關于貨幣政策與商品期貨價格關系，研究文獻卻相對較少。鄭尊信和徐曉光(2013)[32]將庫存理論與Frankel的超調模型結合起來，發現市場利率不僅直接影響資金占有成本，還通過影響均衡庫存間接地影響預期商品價格變動，表明商品市場(Frankel所述的)超調現象和(在持續性緊縮貨幣政策下)調整不足現象可能并存。鄭尊信、王琪和徐曉光(2016)[30]將融資套利因素引入到庫存理論框架中，發現融資套利交易活動扭曲傳統庫存理論觀點下貨幣政策對商品的傳導機制，在緊縮性貨幣政策下強化商品市場的“調整不足”現象。此外，也有部分學者注重于實證分析方面，為我國貨幣政策傳導機制的研究提供現實依據。王錕(2013)[24]運用SVAR方法分析國內商品期貨市場時發現，貨幣政策的變動會對商品價格指數產生較大影響。但該學術觀點也存在爭議，如晁增義和諶金宇(2015)[22]發現市場利率調整對商品價格的影響較弱，并認為我國利率傳導機制的有效性不足。

回顧海內外文獻發現：商品期貨定價研究中，市場利率被視為狀態變量和外生性因素，研究側重商品期貨定價，未能系統解釋市場利率對商品期貨價格的影響機制；市場利率與商品價格的關系研究中，理論框架(如超調模型或融資套利效應模型)主要在理論層面系統解釋市場利率與商品價格的影響機制，而在實證層面統計檢驗主要針對理論框架的邏輯結果，而非理論框架中的影響機制。因此，以往研究主要采用商品期貨數據間接地觀察市場利率的沖擊響應結果，未能在實證中細致檢驗內在影響機理。本文將期貨價格中隱含的利率過程提取出來，借助該通道直接觀察商品價格對宏觀信息沖擊的反應，尤其是市場利率在商品市場的內在傳導機制，進而分析貨幣政策對商品價格的作用機理，主要貢獻在于：在理論框架上，不僅考慮到我國利率市場化的進程，更直接將影響機制嵌入到商品期貨定價當中，實現定價模型與影響機制的有機結合，進而模擬實際市場利率對商品價格的作用機理；在實證分析上，借助卡爾曼濾波方法在商品期貨定價模型實證分析中系統檢驗影響機制。

理論框架

商品期貨定價模型主要借助Ross(1976)[15]的APT框架，其核心在于線性因素模型和無套利分析框架。庫存理論認為，商品期貨價格有三個影響因素：

(1)市場利率r，代表持有庫存的機會成本。Gibson and Schwartz(1990)[10]在三因素模型中首次引入隨機利率CIR過程，此后該假設被學界廣泛采用(見Brennan,1991；Schwartz,1997；Schwartz and Smith，2000)[4][16][17]。但需要指出的是，我國利率市場化改革尚處于推進當中，貨幣市場分割現象明顯，理論模型中設定的無風險利率與市場利率差異明顯，各類商品領域的庫存持有者，在貨幣市場進行借貸的市場利率迥異。三因素模型中，市場利率被設定為狀態變量，而非采用真實市場利率，具有現實合理性，可視為特定商品領域期貨價格對市場利率的平均反應。

(2)便利收益δ，源于商品期貨市場中逆倉儲費用的典型現象。為了解釋逆倉儲費用，Kaldor(1939)[11]、Working(1949)[20]引入便利收益概念，隨后Brennan(1958)[3]在他們的研究基礎上提出庫存理論。庫存持有者雖然需要支付商品庫存的各項倉儲成本，但商品庫存也為庫存持有者提供便利，可從庫存短缺中獲利或應對臨時需求沖擊，該收益即為便利收益，通常被視為商品中嵌入的期權。當便利收益超過倉儲成本，會出現逆倉儲費用現象。鄭尊信和唐明琴(2013)[29]對便利收益進行了系統回顧。

(3)現貨價格x，代表商品期貨價格中基礎性因素。以上三個因素常用于解釋商品期貨價格的變動。此外，這些因素的不確定性也是市場風險的主要來源。所以，Brennan(1958)[3]提出應在定價模型中考慮各因素對應的風險溢價。風險溢價是各影響因素不確定性形成的風險補償，實證模型中進行等價鞅測度變換時需假設風險溢價形式。

由于Liu and Tang(2011)[13]模型具有涵蓋單一商品期貨定價模型的主要優點，本文選擇該模型作為商品期貨定價模型的基準框架。在仿射期限結構框架下，商品期貨定價形式為：

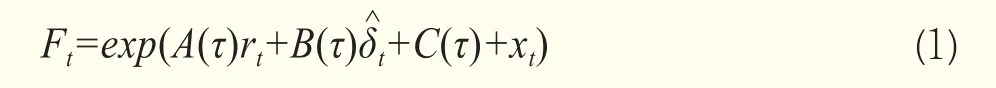
其中，τ是期貨合約的到期期限，A(τ)，B(τ)，C(τ)分別是τ的未知函數，A(τ)和B(τ)分別代表利率和便利收益對期貨價格對數的影響函數，而C(τ)則代表了剔除三個因素影響后對數期貨價格的期限函數。

假定商品的現貨價格和便利收益都遵循Ornstein-Uhlenbeck隨機過程，市場利率過程遵循CIR過程。由于市場利率會影響庫存水平，進而與便利收益密切相關，通常假設便利收益和市場利率之間存在相關性。同時，現貨價格分別和便利收益、隱含利率存在聯系。盡管理論上市場利率影響庫存和現貨價格，但利率在商品期貨市場的反應機制有待理清，商品期貨價格的隱含利率過程難以從市場上直接觀測，因此模型中的利率CIR過程并非現實市場利率而是期貨價格的隱含利率，并將其視為一個隨機狀態變量。為了觀察現實市場利率在商品期貨市場的反應模式，分別將隱含利率過程的長期均衡水平和波動率設定為現實市場利率信息的函數，即θr,t=θr(it-1)和σr,t=σr(it-1)。至于風險溢價，部分學者提出了設置方式。Schwartz(1997)[16]將風險溢價設為常數，Duffee(2002)[6]、Duffee and Stanton(2012)[7]、以及Casassus et al.(2005)[5]則將風險溢價設定為狀態變量的線性函數。參照Liu and Tang(2011)[13]，將風險溢價設為狀態變量的平方根，從而確保在現實測度下聯合隨機過程的仿射形式。具體地，風險溢價向量為：

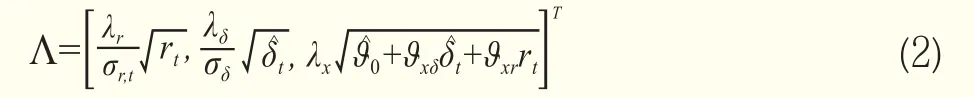
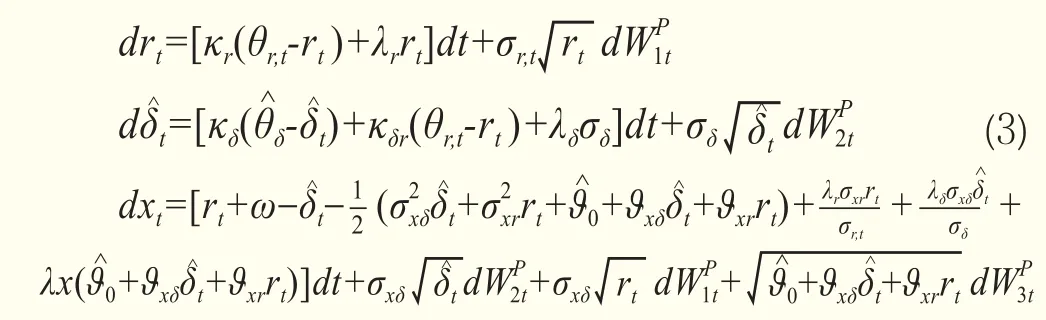
其中，rt是商品期貨市場的隱含利率，δt是商品便利收益且是對數商品現貨價格。κr和κδ均為正，分別代表的均值回復速度，則分別為rt和的長期均衡水平。根據定義其中ω衡量便利收益的異方差程度，ω越大意味著便利收益的異方差效應越小。在Q測度和無套利均衡條件下，商品期貨價格Ft應滿足以下偏微分方程：

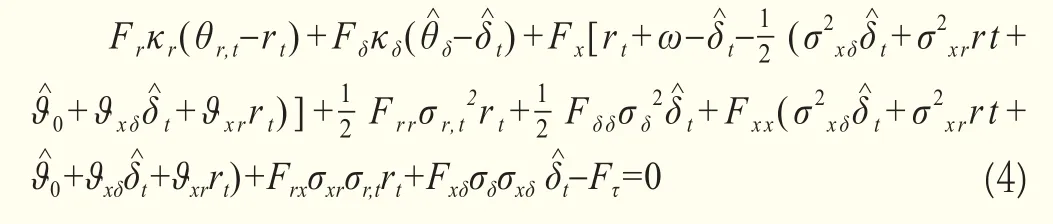
其中，Fr、Fδ、Fx分別是商品期貨對利率、便利收益和現貨價格的一階微分。根據邊界條件即合約到期時商品期貨價格收斂于現貨價格，進而有A(0)=B(0)=C(0)=0。結合邊界條件，求解偏微分方程，得到：

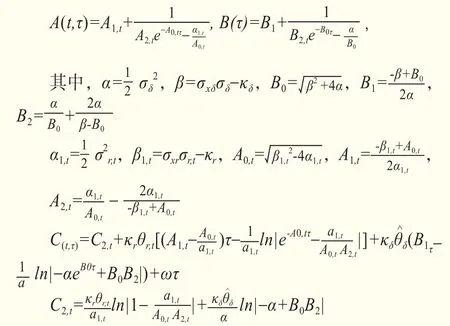
Liu and Tang(2011)[13]模型中，各影響函數A(τ)、B(τ)和C(τ)僅受合約到期期限τ的影響，而不受當前新到達市場信息(實際市場利率)的影響。然而該假定可能與現實市場情況不符，在不同貨幣政策環境下市場利率對期貨合約價格的影響程度可能會發生改變，影響函數A(t,τ)和C(t,τ)均隨市場利率演進。C(t,τ)可分解為如下三部分：

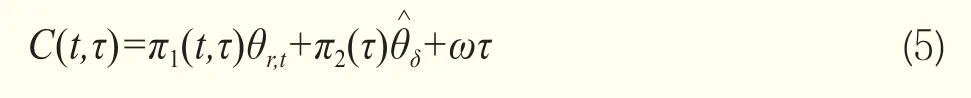
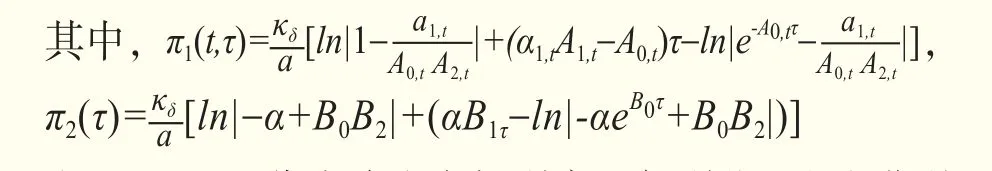
發現，C(t,τ)代表隱含市場利率和便利收益的長期均衡水平對商品期貨合約價格的影響(A(t,τ)rt+B(τ)δ^t則代表了即期影響)，π1(t,τ)和π2(τ)分別衡量兩者對期貨價格的長期影響強度。影響強度不僅依賴于到期期限τ和模型參數，還與現實市場利率信息相關，即當期利率通過θr,t和σr,t機制作用于C(t,τ)函數。Liu & Tang模型假定θr,t為常數，則C(t,τ)退化為C(τ)，該假定違背了市場直覺，即投資者對于隱含利率長期均衡水平的認知會隨著貨幣市場狀態的轉換而發生調整，商品市場則隨著均衡水平調整做出反應并驅動期貨價格變化。

商品市場對貨幣市場環境變化的反應可能不僅僅表現為隱含利率平均水平的變動，也有可能表現出其波動率的變化，為了全面地觀察商品期貨市場對貨幣政策信息的反應機制，有必要進一步考察隱含利率的波動率。通過將隱含利率過程的波動率設定為當前市場利率信息的函數，即σr,t，可發現A(t,τ)和π1(t,τ)都依賴于信息it-1，意味著，如果現實市場利率影響到隱含利率的波動率，那么該影響將通過改變即期隱含利率及其長期均衡水平對期貨價格的影響強度，最終傳遞到商品期貨價格。

概括地，貨幣政策對商品期貨市場的作用機制有三個渠道：其一，作用于隱含利率過程對期貨價格的影響函數A(t,τ)；其二，作用于隱含利率長期均衡水平θr,t；其三，作用于隱含利率長期均衡水平對期貨價格的影響強度π1(t,τ)，最終傳遞到商品期貨價格。因此，作用機理分短期影響和長期影響，第一作用渠道主要產生短期性影響，第二、三渠道主要施加長期性影響。

實證分析

一、數據描述

選取我國期貨市場上交易的銅、鋁、鋅、燃料油、天然橡膠和大豆(豆一)六類商品期貨合約，以及五種到期期限的期貨合約，標記為F0，F1，F2，F3和F4，其中F0表示近月連續合約，而F1表示1月連續合約，以此類推。考慮到到期期限過長的合約通常缺乏流動性，很難確定是否能夠提供真實的市場信息，故未納入實證樣本。樣本區間從2007年9月18日～2015年7月27日，每個合約的樣本容量為1909個，樣本期間涵蓋市場利率完整的波動周期以及2008年全球性金融危機。鑒于SHIBOR具有良好的市場代表性、基準性和穩定性(項衛星和李宏瑾，2014)[26]，在研究中被廣泛采用，本文也采用SHIBOR3月數據作為模型的市場利率。采集的數據源于WIND資訊。

二、實證模型中的θr(it-1)和σr(it-1)設定

市場利率雖然不宜直接作為商品價格的影響因素，因反應市場資金面狀況可作為觀察狀態變量隱含利率過程的信息。為進一步考察市場利率對商品價格隱含利率過程的影響，需具體化θr(i(t-1)和σr(i(t-1)的函數形式。出于簡便的考慮，采用線性模型：

其中，it-1為t-1時刻觀察到的市場利率。市場利率處于低位時，意味著貨幣市場處于較為寬松狀況，按照庫存理論，庫存占用成本呈現下降趨勢，此時商品期貨隱含利率長期均衡水平與市場利率傾向于正相關關系，φ2取值為正。然而，鄭尊信、王琪和徐曉光(2016)[30]提出，當商品融資套利活動活躍、套利庫存高企時，融資套利效應可能在商品市場占主導地位，此時商品期貨隱含利率長期均衡水平和市場利率也可能出現負相關關系，即φ2的值為負。

同時，假定隱含利率波動率在觀測期內并非常定不變，而是與隱含利率長期均衡水平一樣能及時對市場信息(市場利率)做出調整，并建立如下關系：

式(6)主要考察市場利率對商品期貨隱含利率長期均衡水平的影響，而式(7)則主要檢驗市場利率對隱含利率波動率的影響，進而觀察商品期貨市場隱含利率的波動性在不同貨幣市場狀況下的表現。

三、參數估計方法

參數估計難點在于模型中決定因素(隱含利率、便利收益和現貨價格)為狀態變量，難以直接觀察。為此，學界通常使用校準方法解決，常用校準方法有有效矩估計、極大似然估計和卡爾曼濾波方法。盡管模型中的狀態變量都難以直接觀察，但通常遵循馬爾科夫過程，因此使用卡爾曼濾波方法來估計定價模型的參數是恰當的。

觀測方程給出可觀察到變量與不可觀測狀態變量的聯系。觀測方程為：

在卡爾曼濾波校準模型中，狀態方程描述不可觀察狀態變量的動態過程。由真實概率測度下狀態變量動態過程，可得到其隨機過程的離散形式：

表1 卡爾曼濾波方法下的參數估計結果

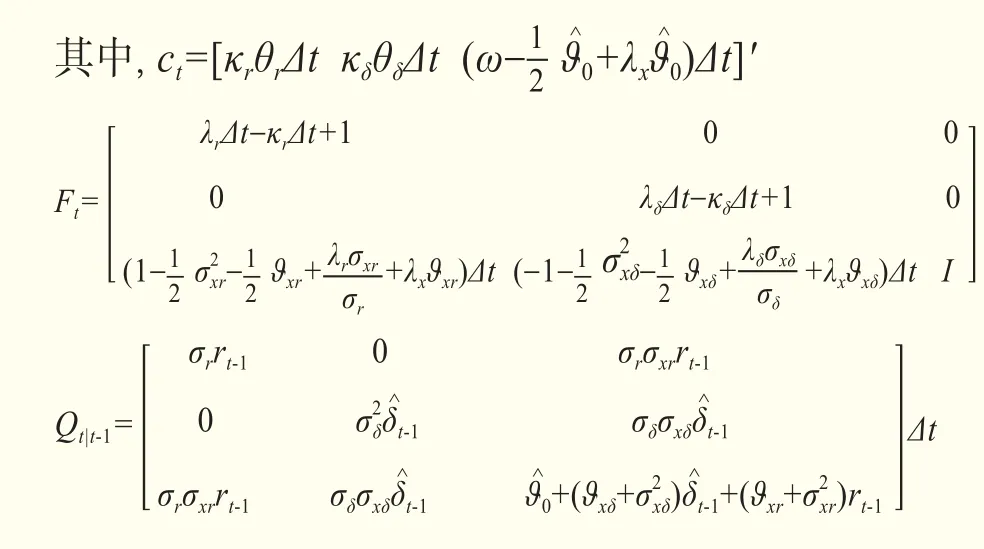
其中，Vt是均值為零，協方差為Qt的序列不相關高斯擾動向量。狀態變量的協方差矩陣Qt具有時變特征且以前期信息為條件。

應該注意的是，以θr(it-1)=φ1+φ2it-1函數形式將市場利率信息納入定價模型時，C(τ)函數形式將依據條件信息而動態調整，應該記為C(τ,t)。同理，以σr(it-1)=γ1+γ2it-1函數形式將市場利率信息納入定價模型時，C(τ)和A(τ)函數形式將依據條件信息而動態調整，應該分別記為C(t,τ)和A(t,τ)。已知狀態變量的高斯轉移密度以及觀測方程誤差項分布，使用拓展卡爾曼濾波算法可推導似然函數，通過最大化似然函數估計模型參數。

實證結果與分析

實證過程中，首先考慮θr(it-1)=φ1+φ2it-1，σr(it-1)=σr的情況。通過卡爾曼濾波方法可獲得模型參數的估計值，進而可計算影響函數A(t,τ)，B(t,τ)和C(t,τ)。參數估計結果如表1所示。

從參數估計結果可以看出，在5%顯著性水平上模型參數大多數顯著不為零，說明定價模型設定背后的理論依據基本可靠。高度顯著的κr和κδ實證支持隱含利率過程和便利收益過程的均值回復特性。所有商品的ω都接近于零，表明商品市場普遍存在便利收益異方差性。

選取的6種商品中有4種商品在5%顯著性水平上模型參數φ2顯著不為零，說明商品期貨隱含利率長期均衡水平會對實際市場信息做出相應調整。一般情況下，較高市場利率意味著緊縮的貨幣市場狀況，根據庫存理論，商品期貨隱含利率長期均衡水平和市場利率傾向于正相關關系，樣本商品中僅大豆支持該實證結論，而且放大10倍的φ2估計值為3.9331，實際估計值為0.39331，表明商品期貨市場在吸收市場利率信息過程中會降低市場信息效應。

與大豆所示情況不同，樣本商品中有色金屬數據估計的φ2值均顯著為負，表明市場利率降低時有色金屬期貨隱含利率長期均衡水平有上升趨勢。這表明商品貿易融資因素可能是我國商品期貨市場驅動力之一。銅、鋁和鋅等金屬因其良好特性常被視為優質的融資抵押物。貨幣市場市場利率走高往往促進貿易融資活動，由此拉動庫存需求(作為抵押物)從而降低預期商品價格變動。通過貿易融資獲得資金通常用于套利活動，可能流向理財產品、信托產品、房地產行業及網絡借貸等領域。

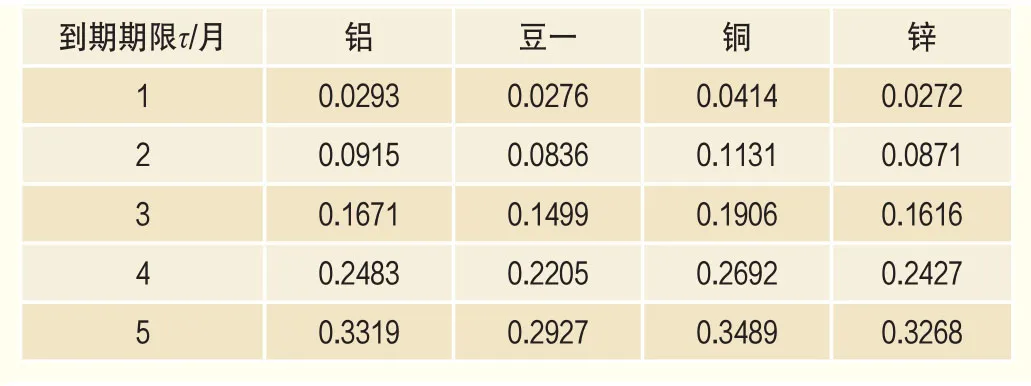
表2 各商品的π1 (τ)的期限結構

鋁、銅、鋅和大豆等樣本商品中模型參數φ2取值顯著不為0，也表明市場利率會對商品定價模型中的C(t,τ)施加影響。該影響程度不僅取決于模型參數φ2的取值，還取決于θr的系數函數π1(τ)。由于表1中σr為固定不變的常數，π1(τ)僅依賴于期貨合約的到期期限τ，參數估計結果可推斷出π1(τ)的期限結構，如表2所示。表2僅顯示φ2取值顯著的樣本商品π1(τ)的期限結構，主要是因為此類商品為考察重點。

不難發現，各類商品π1(τ)的期限結構遵循相似模式，隨著到期期限的增加，π1(τ)函數值逐漸增大，這與市場邏輯基本符合。期限較短的期貨合約而言，市場利率引起的隱含利率長期均衡水平改變對商品期貨價格影響相對較小，從而市場利率對期貨合約價格起到反向作用且影響較小。而期限較遠的期貨合約而言，市場利率引起的長期均衡水平改變對商品期貨價格影響相對較大。

表3給出θr(it-1)=θr，σr((it-1)=γ1+γ2(it-1)設置下模型參數估計結果。對于天然橡膠，市場利率對隱含利率方差的系數γ2在5%的顯著水平上不顯著，表明市場利率水平到隱含利率波動率的信息傳遞機制受阻。天然橡膠行業內資金價格的波動性對市場利率的變化在統計意義上沒有反應。考慮到表1的參數估計結果中市場利率對天然橡膠隱含利率長期均衡水平的影響系數同樣不顯著，說明天然橡膠期貨價格隱含利率過程對市場信息的沖擊反應非常遲鈍，市場利率信息的傳導機制幾乎阻滯。其他樣本商品的隱含利率波動率和市場利率都表現出強烈的負相關關系，尤其是有色金屬銅、鋁和鋅，其參數γ2放大10倍的估計值分別高達-181.73、-62.9786和-48.8524，反映出寬松貨幣環境往往伴隨著商品價格的劇烈波動。

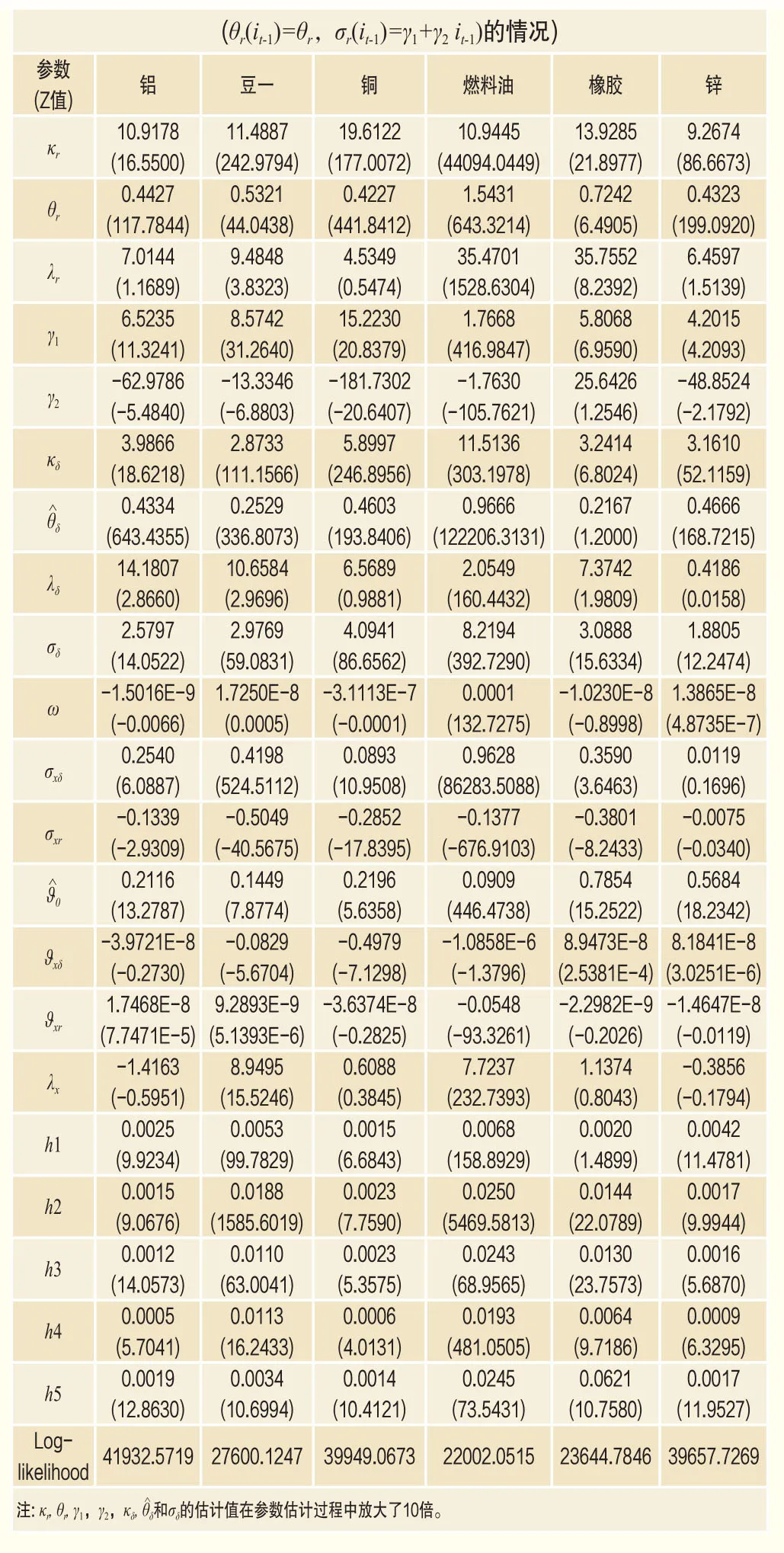
表3 卡爾曼濾波方法下的參數估計結果

圖1分別展示，依據表3估計參數結果模擬的市場利率與A(t,τ)的關系曲線，將市場利率對A(τ)的影響以更直觀方式進行描述:隱含利率波動率如何吸收市場利率信息，進而對商品期貨價格的施加影響。

圖1可以發現，低利率市場環境中，商品期貨價格中A(t,τ)函數傾向于更大的取值，且該結論與各到期期限無關。不同類別的樣本商品對應的市場利率與A(t,τ)關系曲線各不相同，作為農產品的大豆和作為工業品的燃料油，該關系曲線近乎呈現為一條水平直線，A(t,τ)的大小基本上不受市場利率的影響；而對于同為有色金屬的銅、鋁和鋅，市場利率與A(t,τ)關系曲線基本遵循同一模式：市場利率對A(t,τ)的影響為負向，較低的市場利率對應較高的A(t,τ)函數值。回顧表3，γ2均為負數，這意味著市場利率對隱含利率波動率的影響為負向，市場利率下行時隱含利率波動率有升高的趨勢。在此情形下，投資者希望得到更高的風險溢價作為其承擔高風險的補償，如果其他因素保持不變，那么投資者這種意愿在市場上則表現為有更大的A(t,τ)函數值。銅、鋁和鋅的市場利率與A(t,τ)關系曲線很好地印證了這一市場邏輯。綜上表明，市場利率對A(t,τ)函數影響因商品而異，大豆和燃料油的A(t,τ)函數對市場利率變動不敏感，而對于有色金屬，市場利率對A(t,τ)函數影響均為負向。

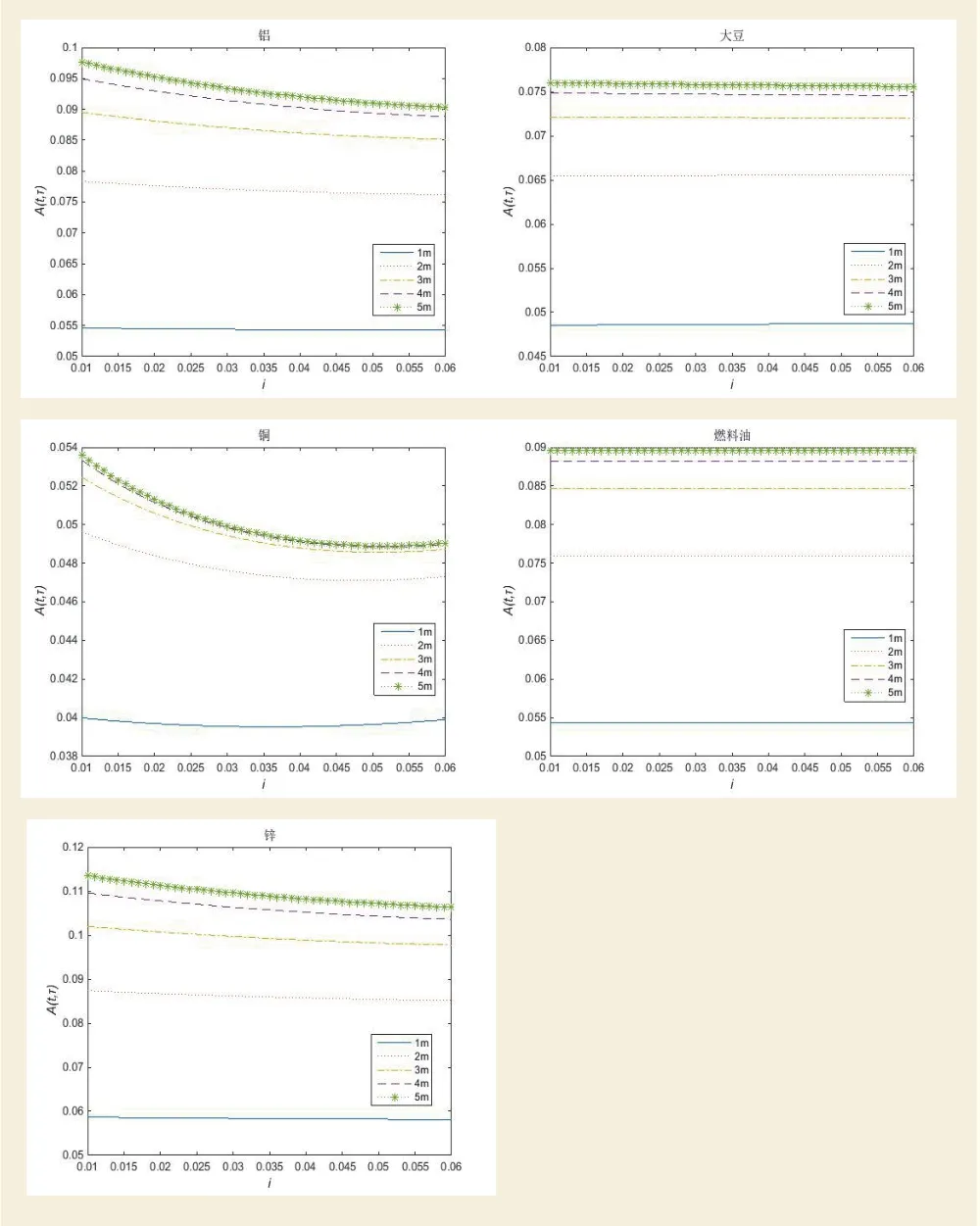
圖1 基于表3參數估計結果模擬的A(t,τ)

采取類似方法，模擬市場利率與C(t,τ)的關系曲線，發現相同商品同一到期期限期貨合約的C(t,τ)受市場利率影響較小，根據各到期期限而描繪的關系曲線近似呈現為一組相對平行的水平線。而到期期限τ對π1(t,τ)函數影響明顯，而且各到期期限呈現的π1(t,τ)曲線差別在各商品中卻有著相似的表現，因而可推斷到期期限是影響π1(τ)的主要因素。結合市場利率與A(t,τ)和π1(t,τ)函數關系分析時發現，隱含利率波動率吸收市場利率信息后，對商品期貨價格的傳遞主要是通過隱含利率對商品價格的影響函數(A(t,τ))而非隱含利率長期均衡水平的影響函數π1(t,τ)。

表1和表3的實證結果都證實，隱含利率過程明顯異于市場利率過程。表1中大豆、銅、鋅、鋁、天然橡膠和燃料油的φ1，表示隱含利率過程漂移項不受市場利率影響的部分，在1%顯著性上平上顯著。實證比較后還發現，市場利率借助隱含利率波動率主要作用于第一影響通道(短期機制)，而通過隱含利率長期均衡水平主要作用于第二和第三影響通道(長期機制)。

結論

我國利率市場化改革尚在推進中，市場利率不宜直接作為商品期貨價格的影響因素，但其蘊含了貨幣市場資金狀況的重要市場信息。為了研究利率市場化進程中市場利率如何影響商品價格變動，本文借助商品期貨定價模型的隱含利率過程，將市場利率的信息響應機制納入到隱含利率動態過程。采用六種商品期貨合約進行實證研究，結果表明：(1)商品市場利率的信息傳遞機制依賴于商品種類，不同商品期貨隱含利率對市場信息的響應機制有所差異；(2)隱含利率過程與市場利率迥異，因存在貿易融資套利等現象，不能簡單地將市場利率視為商品期貨市場的無風險利率；(3)天然橡膠期貨價格隱含利率過程對市場利率信息的沖擊響應遲鈍，市場信息傳導機制幾乎被阻滯；(4)在貨幣市場資金趨緊時，鋁、銅、鋅等商品因貿易融資套利效應導致庫存需求增加，隱含利率有上漲趨勢；貨幣市場趨于寬松時隱含利率傾向高波動性。(5)貨幣政策影響商品期貨價格的渠道主要有：市場利率信息被隱含利率長期均衡水平吸收從而改變長期基差水平；市場利率信息影響隱含利率波動率進而影響隱含利率對基差的影響程度。Barsky和Kilian(2004)[2]、Akram(2009)[1]以及Scrimgeour(2015)[18]均發現，市場利率和商品價格存在負向的相關關系，上行的市場利率或者緊縮的貨幣市場狀況往往伴隨著下跌的商品價格。本文實證研究卻發現，在市場利率上行時隱含利率有反向下行的趨勢，預期商品價格變動收窄，當期商品價格下跌受阻，這與鄭尊信、王琪和徐曉光(2016)[30]提出的貿易融資套利效應相互佐證。

研究局限性在于：市場利率對商品價格的作用機制，僅考慮隱含利率通道，并采用線性模式，研究設計相對簡單，有待進一步考慮更為復雜的影響機制；研究當中忽視商品金融化帶來的可能影響。這將成為下一階段的研究方向。