基于深度增強學習的自動游戲方法

,,,，

(長江大學信息與數學學院，湖北 荊州 434023)

基于深度增強學習的自動游戲方法

袁月,馮濤,阮青青,趙銀明，鄒健

(長江大學信息與數學學院，湖北荊州434023)

增強學習近年來多被用于智能體自動游戲，但增強學習在面對過大的狀態或者行動空間時不能很好地處理。深度增強學習結合深度學習的感知能力和增強學習的決策能力，可以有效解決環境復雜問題。將增強學習與深度學習結合，通過改進的Markov決策過程逐步學習最優策略。首先找到目前的環境中最有價值的狀態，從而產生最大積累獎勵的行動，然后通過利用深度增強學習方法訓練計算機自動完成一個簡單游戲，使用控制變量法分別分析迭代次數和游戲難易程度對游戲得分的影響。試驗結果表明，在外界環境相同時，準確率隨著試驗迭代次數的增大或游戲難度的減弱而增大，從而驗證了智能體可以通過外界因素的改變進行更有效訓練，最終獲取最優結果。

深度增強學習；自動游戲；智能體

近年來，深度學習已經成為人工智能領域的研究熱點，其主要思想是通過訓練深度神經網絡，從高維數據中提取數據的深層特征[1]。增強學習作為一種重要的機器學習方法，其目的在于根據不同目標構造一個最優策略。即當智能體(Agent)處于某種動態的未知環境時，通過與環境狀態的交互作用，以環境反饋為輸入，然后不斷學習，改進自身性能并調整行為，最終使所獲的累計獎勵最大化[2，3]。深度增強學習結合深度學習的感知能力和增強學習的決策能力，引起了研究者的廣泛關注，形成了人工智能領域新的研究熱點，在游戲、機器人控制、機器視覺等應用領域都有著廣泛的應用[4，5]。下面,筆者利用深度增強學習方法訓練計算機自動完成一個簡單游戲，并且分析訓練次數對游戲得分的影響。

1 算法描述

1.1策略

Agent執行每一步所獲得回報，該回報是對后面每個狀態的影響的總和，狀態是指Agent在某時刻所能觀察到的環境狀況，狀態決定下一步的動作，動作又對應著一種狀態，因此狀態和動作存在某種映射關系，這個過程稱為策略。策略用策略函數表示為：

at=π(st)

(1)

式中，st是時刻t的圖像輸入，即Agent在時刻t的狀態；at是Agent下一步的行為。

Agent根據自己觀測到的st選擇一種行為at，環境接收到at后，會更新狀態為st+1。在這個游戲里，增強學習的任務就是找到一個最優策略，使得累積回報達到最大。

通常，為了簡化增強學習模型，將該模型表示為一Markov過程，即下一狀態僅取決于當前的狀態和當前的動作。因此，狀態由來自游戲的幀序列(由于人眼的視覺暫留特性)以及玩家最近一次的動作(而并非之前所有動作)確定。為確定下一狀態，需要定義一個函數，并求出其最優值，即最優動作價值函數。

1.2最優動作價值函數

因為動作對應的狀態唯一，而狀態對應的動作不唯一，因此用動作產生的回報更有利于找到最優策略。而一個行為產生的獎勵肯定發生在行為之后，可以用一個價值函數來定義動作的潛在價值，即對未來回報的期望，表示為：

Qπ(s,a)=E[Rt|st=s,at=a,π]

(2)

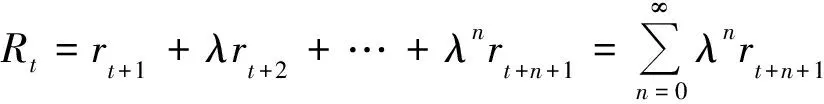
Q*(s,a)=arg maxπQπ(s,a)

(3)

即從所有策略中選擇Q值(即累積回報)最大的。計算最優Q值需要進行大量試驗，鑒于試驗的復雜性，可以通過使用Bellman方程迭代更新得到最優Q值，即：

Q*(s,a)=Es′[r+λmaxa′Q*(s′,a′)|s,a]

(4)

式中，r是t時刻的獎勵；maxa′Q*(s′,a′)是使t+1時刻的a′達到最大的Q值。顯然，當前狀態下是無法得知下一步情況的，但上一步的狀態可以得到，因此可以通過每次迭代新得到的r和之前的Q值更新Q值：

Qi+1(s,a)=Es′[r+λmaxa′Qi(s′,a′)|s,a]

(5)

理論上可以證明，當i→∞時，Qi→Q*[7]。

在求解最優動作價值函數時，每次迭代都要將所有的Q值更新一遍，而在此過程中只有有限的樣本提供給系統，為了減小估計誤差造成的影響，不直接將目標Q值賦給下一個，而是嘗試用一個神經網絡來近似Q-函數，這個神經網絡其實就是一個卷積神經網絡，稱為深度Q-網絡(DQN)[8，9]。

1.3深度Q網絡

首先，定義一個用于訓練DQN的損失函數:

(6)

其中，要更新的目標是Q網絡，θ是神經網絡的權重。可以計算出損失函數對參數θ的梯度為：

(7)

Q(st,at)+α(Rt+1+λmaxaQ(st+1,a)-Q(st,at))→Q(st,at)

(8)

式中，α是學習率。

1.4經驗回放

為了保證算法的穩定收斂，在訓練過程中添加了經驗回放技術。時刻t的經驗表示為et=(st,at,rt,st+1)。將時刻t之前的所有經驗都存儲在Dt中，稱為回放記憶，表示為Dt={e1,e2,…,et}，這樣有利于調用學習，大大提高學習效率。每次迭代對神經網絡的參數θ進行更新時，就從Dt中隨機抽取一小批經驗，幫助神經網絡的培訓。抽取經驗樣品的隨機性避免了相鄰經驗的過度耦合，使其不再受價值函數波動對環境的影響，同時，Dt也為式(6)中的2個Q-網絡提供了不同時刻的輸入狀態和動作，為計算損失函數提供了回報r。

1.5初始動作的選擇

在游戲中，初始動作也需要一個策略來生成，通常有2種做法：一是隨機生成一個動作，二是根據當前的Q值得到一個最優的動作，表示為：

π(St+1)=arg maxaQ(St+1,a)

(9)

前者相當于探索未知，有利于Q值的更新，獲得更好的策略，而后者利用之前的策略，相對前者對Q值的更新稍弱。筆者把探索與利用相結合，稱為ε-貪婪法，ε是指探索的概率，這將鼓勵Agent在開始不知道如何玩游戲時大量探索，此時狀態空間是非常大的。接著它做大量的隨機動作，并開始計算在不同的狀態下哪些動作更好，從而利用更多，并試圖縮小最佳的行動范圍。通過更改ε的值可以調整探索與利用的比例。

綜合以上步驟，得到訓練游戲的帶經驗回放深度增強學習算法如下：

初始化經驗回放D，容量為D

初始化動作估值函數Q，隨機初始化參數

for episode =1,…,Mdo

初始化狀態S0，并用特征提取器進行預處理φ1=φ(S0)；

fort=1,…,Tdo

以ε的概率選擇一個隨機動作at

或是根據式(9)選擇一個最佳動作

執行at，得到獎勵rt；觀察下一個輸入圖像，得到像素數據xt+1

到達下一個狀態St+1，同樣進行預處理φt+1=φ(St+1)；

添加經驗et=(φt,at,rt,φt+1)到D中

從D中隨機抽樣一批樣品在10至100之間

通過反向傳播和隨機梯度更新DQN。

end for

end for

2 自動游戲方法及試驗

下面,筆者將通過一個游戲來驗證提出的深度增強學習算法的有效性。首先利用Python編寫一個簡單的游戲，如圖1所示，游戲規則如下：在屏幕的左上角有一個小方塊，底部放置了一個可移動的木板，小方塊每移動一步，玩家控制木板左移一步或右移一步或保持不動，待小方塊因碰撞屏幕四壁而改變飛行軌跡最終掉落下來時，觀察木板是否能夠接住小方塊。若木板成功接住小方塊，則能夠獲得分數獎勵且小方塊反彈上去；若木板未能接住小球，則不得分，且小方塊與底部發生碰撞反彈上去。木板接住小方塊的次數越多，則獲得的分數越高。

圖1 游戲在3種不同難度下(困難，中等，簡單)的示意圖

在利用筆者提出的深度增強學習算法訓練時，DQN的結構如下：該網絡采用84×84輸入圖像，第1層是一個卷積層，有32個步幅為4、8×8的濾波器，由整流非線性跟隨；第2層也是卷積層，有48個步幅為2、4×4的濾波器，另一個整流線性單元的濾波器跟隨；第3層是卷積層，具有64個步幅為2、3×3的濾波器，跟隨有整流線性單元。接著是全連接層，具有3456個輸出，最后輸出層也是全連接，具有784個輸出層，每個動作有一個輸出，如圖2所示。算法的相關參數設置如下：首先程序輸入的是屏幕大小為[320，400]，小方塊的大小為[15，15]以及木板尺寸為[50，5]，神經網絡中學習率為0.99，存儲過往經驗的回放記憶Dt為500000，批量設定為100，訓練次數為500000，測試為50000。假設要教會Agent玩這個游戲，輸入以上數據后，對于木板將會輸出3個動作：左、右以及原地不動接小方塊。其次是當小方塊每一個動作完成，會輸出屏幕圖像即每一個游戲畫面，它隱含地包括了所有得分情況的相關信息。最后是小方塊的速度和方向。以上3個方面的因素共同影響著動作的值，進而影響了下一個像素中木板的左右移動方向，用一個神經網絡代表Q函數，以狀態(游戲屏幕)作為輸入和動作作為輸出對應的Q值。

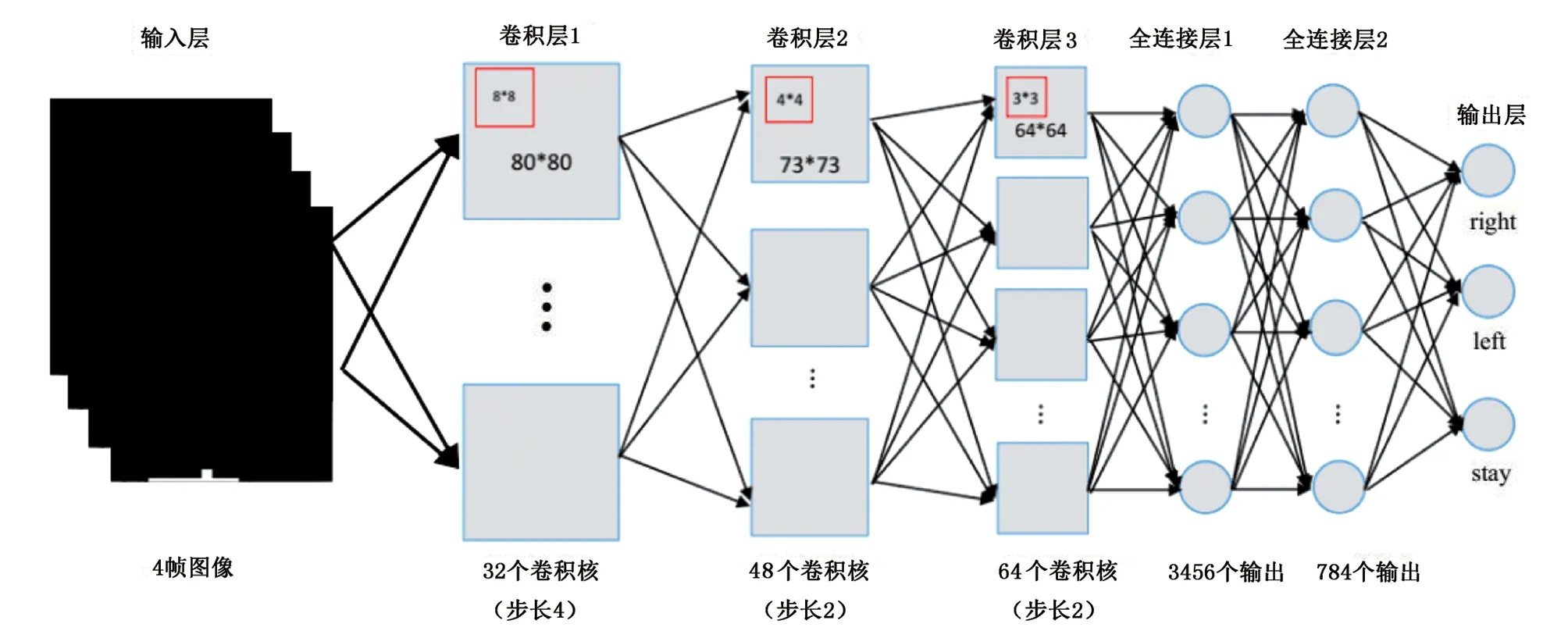
圖2 DQN結構

在試驗中，設置小方塊的大小為15mm×15mm，木板的高度為5mm，長度分別為50、150、250mm，分別對應游戲難度為困難、中等、簡單。由于迭代次數較大，用小方塊的掉落次數表示(小方塊每掉落在底端或木板上一次，迭代次數為上百次)，以木板成功接住小方塊的準確率為試驗結果，如表1所示。

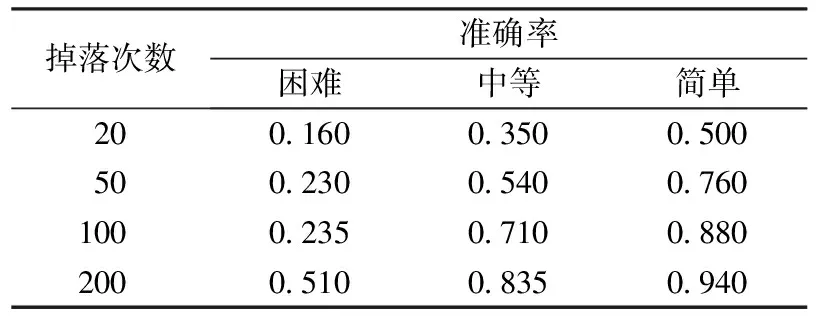
表1 不同環境下的準確率

表1給出了小方塊的掉落次數與不同難易程度的關系，其中小方塊掉落200次對應的木板移動步數大概為50000。由表1可以看出，在不同難易程度中，木板接住小方塊的準確率會隨著掉落次數增大，最終趨于平緩。并且，游戲由簡單到困難，準確率上升的速率也不盡相同。在困難的環境下，準確率上升速率遠遠慢于在簡單的環境下。

圖3表示了在中等難度下木板接住小方塊的準確率的曲線圖，橫坐標依然是小方塊的掉落次數，縱坐標是準確率。首先，由于游戲剛剛開始，準確率會有很大的波動(如木板在第一次就接住小方塊，此時準確率就是100%)，在接近掉落次數單位為12的地方，除了小小的波動，準確率開始以較大的速率增長，慢慢地，在接近掉落次數單位為70的地方，準確率緩慢增長，大概保持在0.83。

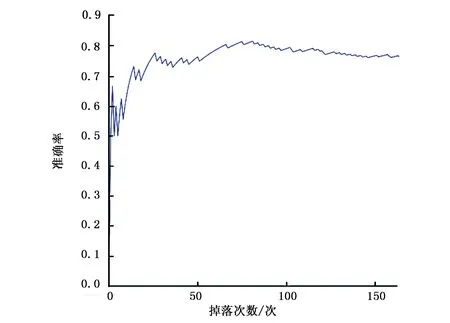
圖3 中等難度下的準確率曲線圖

3 結語

闡述了深度增強學習方法的基本思想，并將其簡單應用在一種自動游戲上，得到了智能體經過訓練的試驗結果，結果表明深度增強學習在進一步的應用上有很大的潛力。在今后工作中，筆者也會嘗試將其進行改進應用在其他游戲中，考查更多結果的影響。當然，自動游戲中的深度增強學習還有不少亟待解決的問題,如如何丟掉那些不利于獲得獎勵的經驗，使其不被從回放記憶中取樣，如何優先處理能導致更好性能的經驗等，這些都有待進一步研究。

[1]孫志軍, 薛磊, 許陽明,等. 深度學習研究綜述[J]. 計算機應用研究, 2012, 29(8):2806～2810.

[2]高陽, 陳世福, 陸鑫. 強化學習研究綜述[J]. Acta 自動化學報, 2004, 30(1):86～100.

[3] 陳學松, 楊宜民. 強化學習研究綜述[J]. 計算機應用研究, 2010, 27(8):2834～2838，2844.

[4] Mnih V, Kavukcuoglu K, Silver D, et al. Human-level control through deep reinforcement learning.[J]. Nature, 2015, 518(7540):529～533.

[5] Sallab A E,Abdou M,Perot E,et al.Deep reinforcement learning frame work for antonomous driving[J].Electronic Imaging,2017(19):70～76.

[6] Mnih V, Kavukcuoglu K, Silver D, et al. Playing atari deep reinforcement learning[J]. Computer Science, 2013，1312(5602):23～32.

[7] Sutton R S, Barto A G. Reinforcement learning I: Introduction[J]. Nature,1998,94720:143～148.

[8]陳先昌. 基于卷積神經網絡的深度學習算法與應用研究[D]. 杭州：浙江工商大學, 2013.

[9]盧宏濤, 張秦川. 深度卷積神經網絡在計算機視覺中的應用研究綜述[J]. 數據采集與處理, 2016, 31(1):1～17.

[編輯]洪云飛

2017-06-28

國家自然科學基金項目(61503047)；長江大學大學生創新創業訓練計劃項目(2016123)。

趙銀明(1965-)，男，副教授，現主要從事應用數學方面的教學與研究工作，452667017@qq.com。

引著格式袁月,馮濤,阮青青,等.基于深度增強學習的自動游戲方法[J].長江大學學報(自科版)，2017,14(21)：40～44.

TP391.4

A

1673-1409(2017)21-0040-05