移動副間隙對兩自由度平面機構非線性動力學的影響

午麗娟

(上海電機學院 機械學院，上海 201306)

移動副間隙對兩自由度平面機構非線性動力學的影響

午麗娟

(上海電機學院 機械學院，上海 201306)

對含間隙移動副的機構非線性動力學行為進行了分析研究。建立了間隙元素非線性接觸碰撞力模型，其正向接觸力采用Hertz彈性力和能量耗散項表征，切向力則由改進的庫侖摩擦力表征；對不同間隙值條件下機構動力學性能進行了仿真分析。結果表明，機構運動穩定性和精度隨著間隙值的增大而降低；相圖和龐加萊截面進一步顯示，隨著間隙值的增大，機構運動具有從周期趨向混沌的非線性特性。

移動副間隙； 動力學響應； 非線性特性

理想運動副忽略了運動副元素之間由相對運動、磨損及公差等造成的間隙，而實際機構中，運動副都含有配合間隙。研究表明[1-3]，受間隙運動副元素之間接觸碰撞的影響，機構運動的穩定性和精度明顯降低。在一定條件下，機構運動還將趨向于混沌而非周期。由間隙引起的這種復雜動力學特性已被廣泛關注和研究。其中，間隙機構建模和仿真、動力學響應預測和分析是研究的兩個主要內容，研究對象多以曲柄滑塊機構和四桿機構為典型機構[4-7]。這些研究表明，不同的間隙建模方法在動力學數值求解中既有優點也有缺點，但仿真結果均顯示機構的非線性特性依賴于系統參數。因此，盡可能精確地建立間隙動力學模型，并計算出系統參數和響應之間的關系依然是一個重要的工作。

在動力學響應方面，文獻[8-10]中對間隙值大小、輸入速度、構件的剛性和柔性、間隙運動副的摩擦和潤滑等進行了研究，以便精確預測影響因子對間隙機構的動力學性能的影響。系統運動的周期性和混沌性則利用非線性方法，如相圖[11]、中心軌跡[12]、龐加萊截面[13]等進行了研究。文獻[14]中以含間隙四桿機構為例，研究了曲柄轉速和連桿真實阻尼對機構周期和混沌運動特性的影響。結果表明，從周期規律運動向混沌的轉變與曲柄的轉速有一定關系；超過某一個特定的值，間隙機構響應呈現非周期性，并對初始條件敏感，而阻尼對響應則影響不大；并推測周期性和混沌運動分別對應于連續接觸和發生碰撞。文獻[15]中利用龐加萊截面和奇特因子研究了不同間隙值下曲柄滑塊機構的動力學特性，考慮間隙存在時，機構動力學響應發生變化，在一定條件下，系統展現非線性混沌特性。文獻[16]中選擇間隙值、曲柄轉速和間隙運動副個數作為影響因子，研究了相應的動力學響應；龐加萊截面和運動副中心軌跡表明，間隙值和曲柄轉速對接觸力、力矩有較大影響，非線性響應與這些因素也密切相關。文獻[17]中研究了間隙大小和曲柄轉速對含間隙曲柄滑塊機構的影響，從滑塊速度和位移的相圖可以看出，混沌運動不僅與間隙值、曲柄轉速有關，與間隙運動副在機構中的位置也有關系。文獻[18]中研究了曲柄轉速恒定、間隙值改變情況下的機構動力學響應；在一定條件下，龐加萊截面展現了混沌、周期和擬周期特性，且間隙值的微小變化將引起龐加萊截面的巨大變化。上述研究的對象多以單自由度機構為主，缺乏對多自由度機構非線性動力學的研究。

本文以兩自由度5桿機構為例，通過對機構中某個構件速度和位移偏離分析，以及長周期運動中，速度和位移參數的相圖和龐加萊截面分析，研究了間隙運動副對機構運動的線性和非線性影響。

1 間隙機構建模

1.1含間隙機構模型

以一個5桿機構為例，理想運動副情況下，其自由度為2，機構如圖1所示。其中，A、B、C、D點分別為4個旋轉運動副中心，E、G分別為BE桿的端點和質心，α、β分別為機構初始角度。

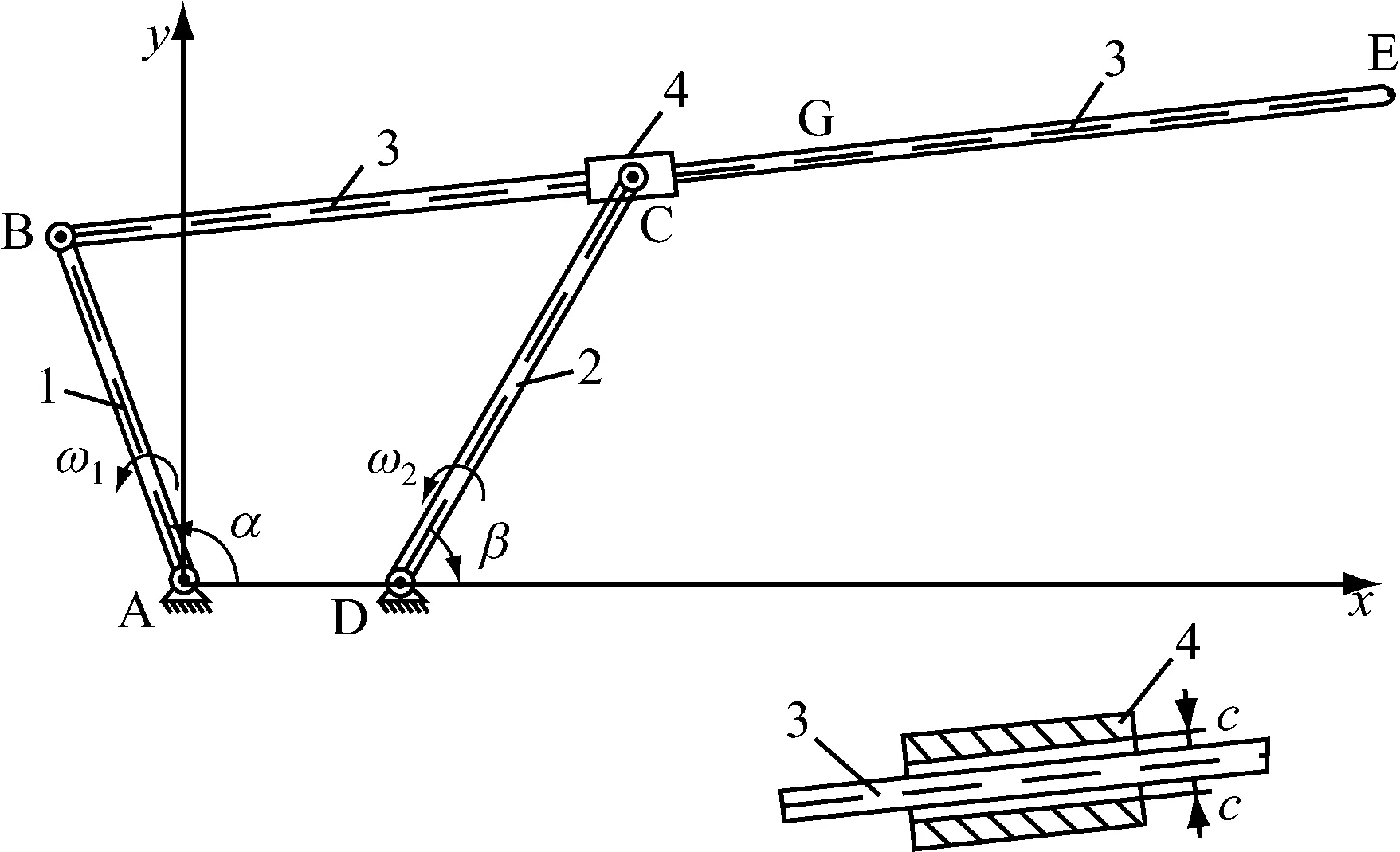
圖1 含移動副間隙兩自由度平面機構

圖1的平面雙曲柄機構由5個剛體桿件、4個理想旋轉運動副和1個帶間隙的移動副組成，桿件1和2 上分別施加兩個轉矩ω1和ω2驅動機構運動。在移動副中，考慮滑塊4和桿件3之間有運動間隙c，其大小為桿3直徑和滑塊4內孔徑之差。各桿件參數如表1所示。

表1 構件基本參數

1.2間隙運動副接觸力模型

由于間隙的存在，運動副兩元素相對運動過程中會產生接觸碰撞，接觸力大小和材料變形與能量損失有關。如圖2所示為間隙運動副接觸點處的接觸變形及接觸力。其中，O1、O2分別為桿3和滑塊4在接觸點橫截面上的回轉中心；t、p為滑塊表面在接觸點彈性變形的初始點和終點；T、N分別為最大接觸變形點的切向和法向；e為偏心距;r為桿3半徑。

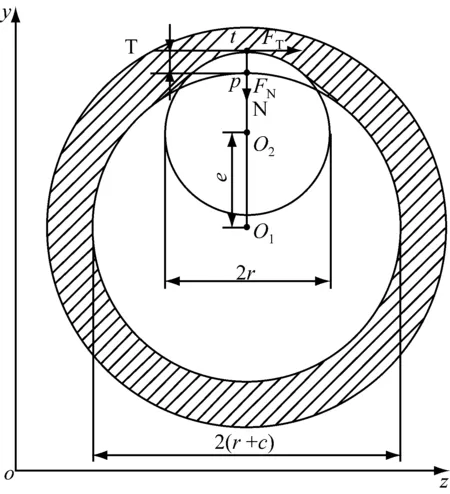
圖2 間隙運動副接觸點處的接觸變形及接觸力

當接觸變形量δ≥0時，兩元素發生接觸碰撞并產生表面彈性變形，滑動約束轉化為施加在接觸碰撞點正向力FN和切向力FT約束。當δ<0時，兩元素分離，約束消除，系統增加2個自由度。圖中，為更清楚地表示接觸變形，進行了放大處理。則

(1)

式中，K為剛度系數，與材料泊松比、楊氏模量及接觸元素幾何特性有關；對于金屬桿件，設指數n=1.5；D為回滯阻尼系數，與δ、最大阻尼系數有關。

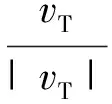
(2)

式中，vT為接觸點處相對切向速度；μ為摩擦系數，與靜摩擦系數μs和動摩擦系數μd有關，即

其中，vd和vs為動摩擦和靜摩擦轉化的絕對速度閾值。

2 仿真結果和討論

基于動力學仿真結果分析不同間隙對兩自由度平面機構動力學特性的影響。機構仿真模型如圖1所示，仿真參數如表2所示，其中，E和ν分別是桿件材料彈性模量和泊松比。

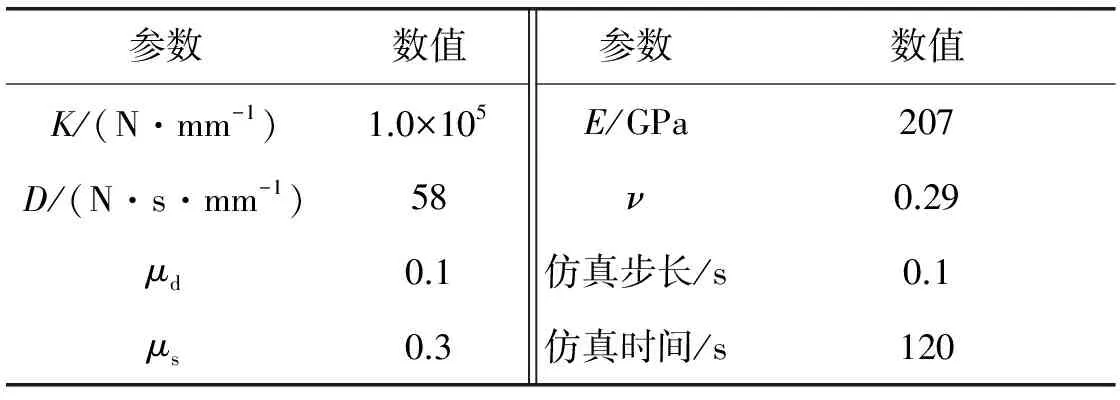
表2 仿真參數

數值計算在ADAMS(Automatic Dynamic Analysis of Mechanical Systems)中完成。為了獲得更快的計算效率和更高的計算精確度，選擇剛性積分器GSTIFF和積分算法I3，積分誤差控制在0.001,仿真時長設置為桿1的10個旋轉周期。

分別取c=0.1，0.2，0.3，0.4，0.5，0.75 mm，桿1和桿2的轉速為ω1=30 d/s和ω2=50 d/s。通過桿3質心點G的速度和位移分析不同c時機構運動穩定性和精確度的變化。進一步對仿真數據進行非線性計算，通過相圖和龐加萊截面分析不同c對機構非線性動力學行為的影響。

圖3所示為桿3質心點G的速度變化。由圖可見，當c=0 mm時，速度曲線光滑；隨著c從0.10 mm逐漸增加到1.00 mm，速度曲線的波動幅度和波動頻率越來越大；且間隙值0.1 mm的微小變化，引起的速度波動卻非常明顯，表明G點速度對初始間隙值非常敏感。

以向量AG表征G點的位置，圖4所示為3個曲柄旋轉周期內G點位置的偏移量，即G點位置相對于c=0 mm理想狀態的偏離情況。由圖可見，當c=0.10 mm時，最大位移偏移量約為0.5 mm；當c=1.00 mm時，最大偏移量接近5 mm，且隨著c從0.10 mm逐漸增加到1.00 mm，位置偏移量越來越大，即隨著c增大，運動軌跡相對于理想狀態時的偏差越來越大。

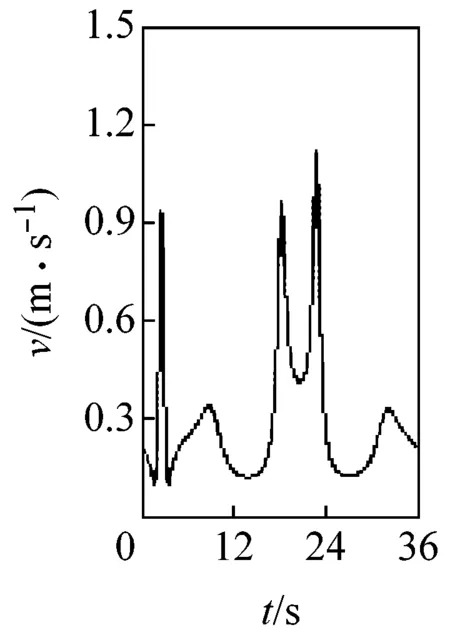
(a)c=0 mm

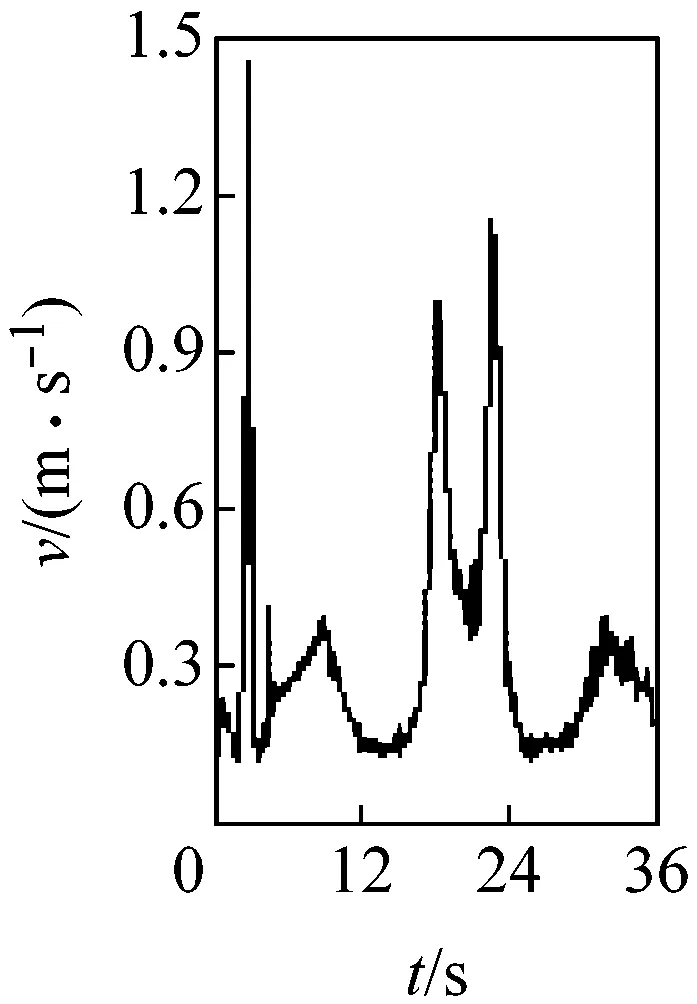
(b) c=0.10 mm

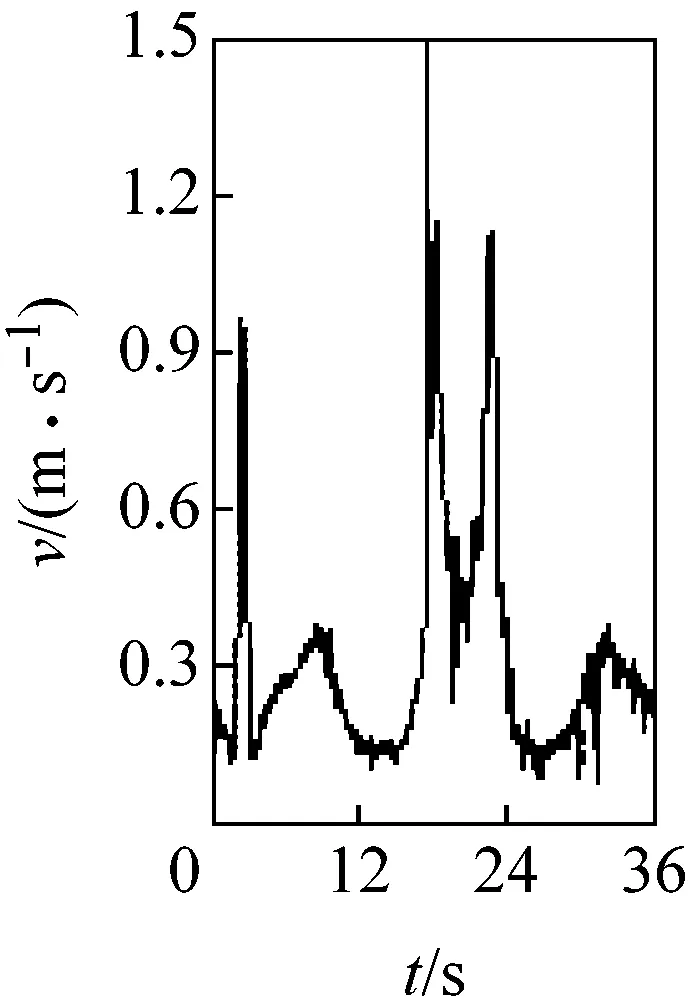
(c) c=0.20 mm

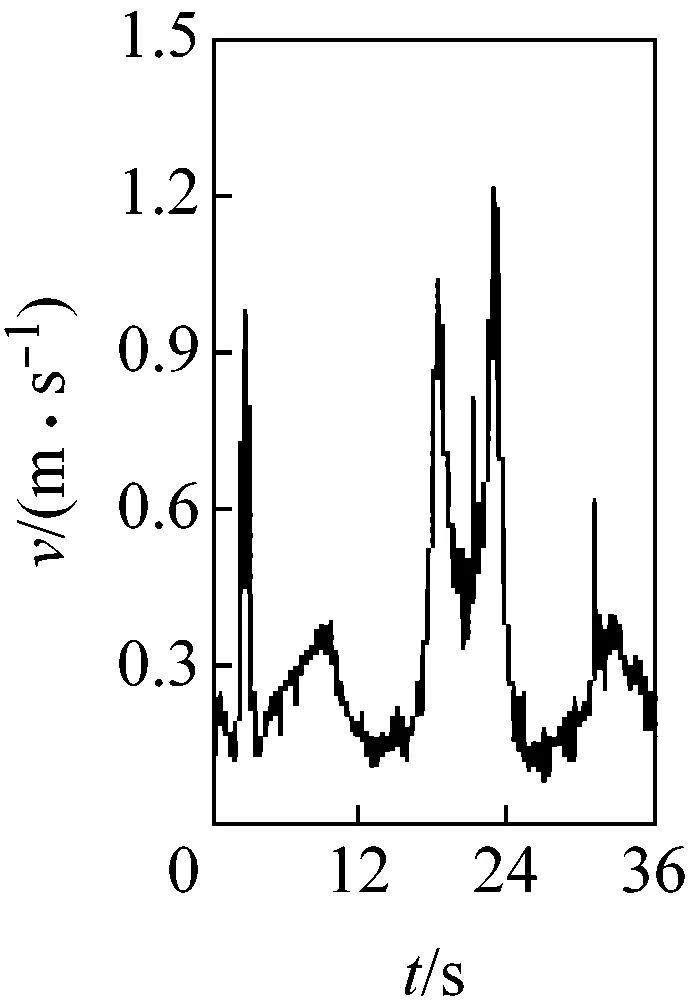
(d) c=0.30 mm

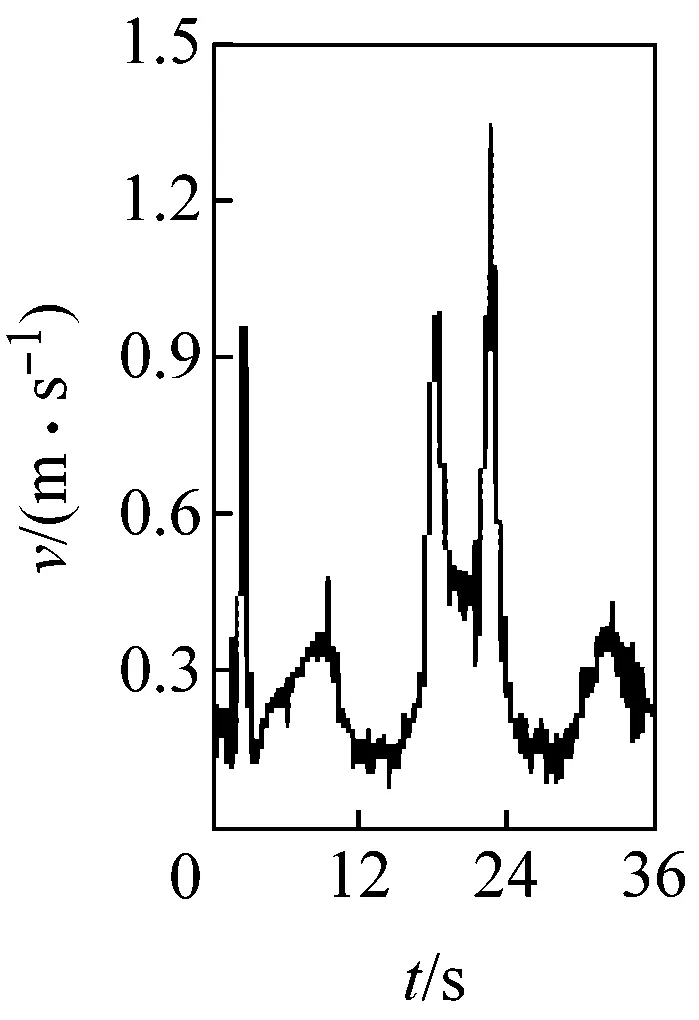
(e) c=0.40 mm

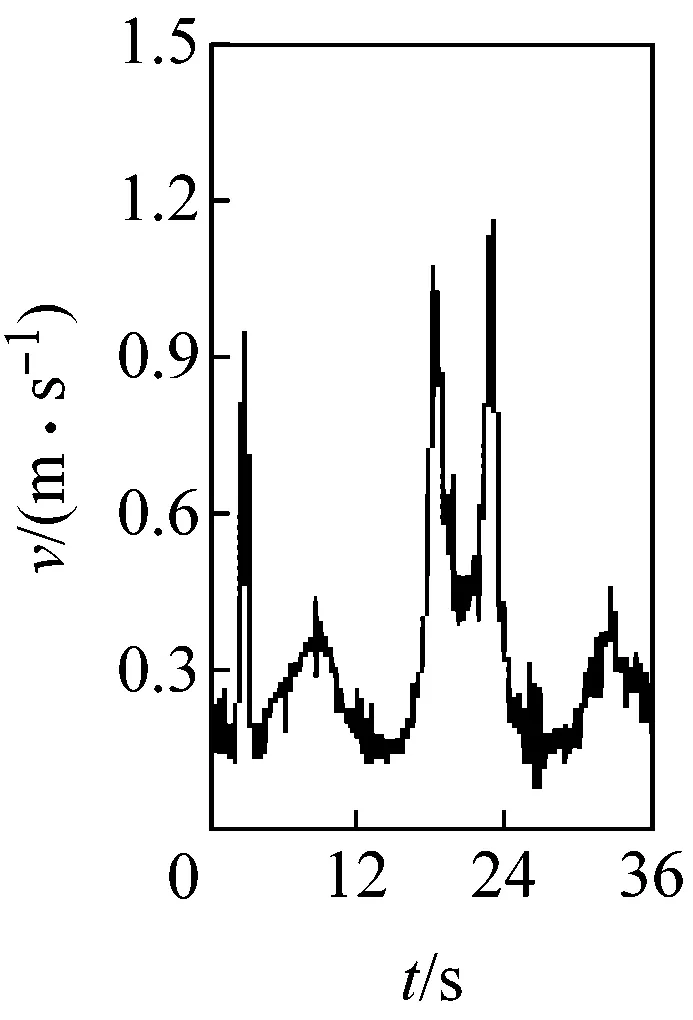
(f) c=0.50 mm

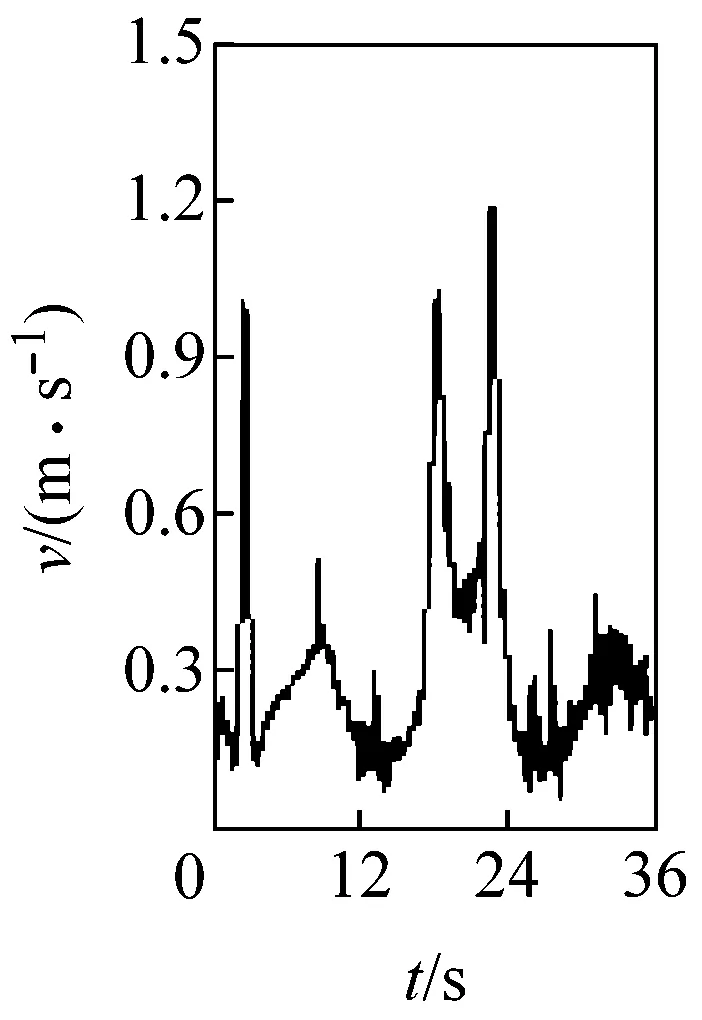
(g) c=0.75 mm

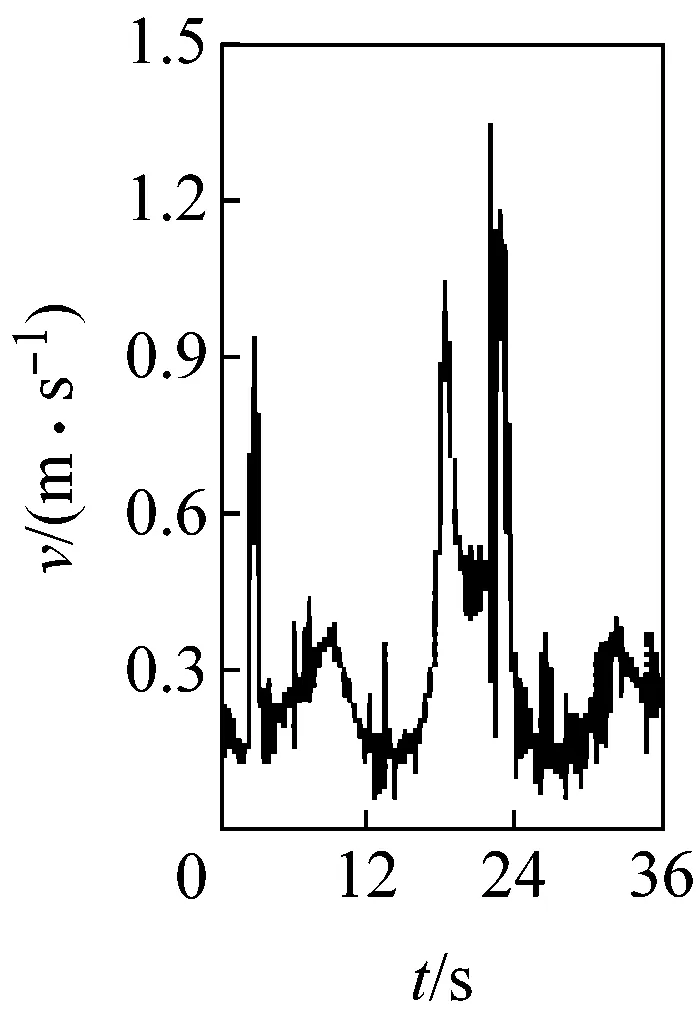
(h) c=1.00 mm

圖3G點速度隨間隙變化圖

Fig.3 Velocity of mass center G at different clearance sizes

圖4 G點位置相對間隙為零時的偏離圖

圖3、4 表明，桿3的運動速度和位移均受移動副間隙的影響，c值增大，運動精度和穩定性下降，這是由于間隙越大，運動副元素間的接觸碰撞越頻繁造成的。

圖5所示為G點速度相對于位移的相圖。由圖可見，當c=0 mm時，相圖軌跡光滑且封閉，機構運動為典型的周期性運動；當c>0 mm時，相圖軌跡波動且不封閉，波動幅度隨c增大而加劇，表明機構運動從周期趨向非周期。圖6所示為G點位移的龐加萊截面圖，其橫、縱坐標rn、rn+1表示G點位移極值的相鄰值。由圖可見，當c=0 mm時，截面上只有一個孤立點，機構運動為可預測的周期性運動；當c>0 mm時，隨著c增大，截面上的點從有限個孤立點逐漸轉變為不可數的密集點分散在整個截面，表明機構運動為擬周期運動和混沌運動。由圖5、6可見，機構動力學行為對初始間隙值非常敏感，并具有非線性特性，這是由于間隙的存在，運動副兩元素之間的相對運動變得不可預測且隨機，導致接觸約束即接觸力和摩擦力具有不確定性，系統由此表現出不可預測的混沌特性。

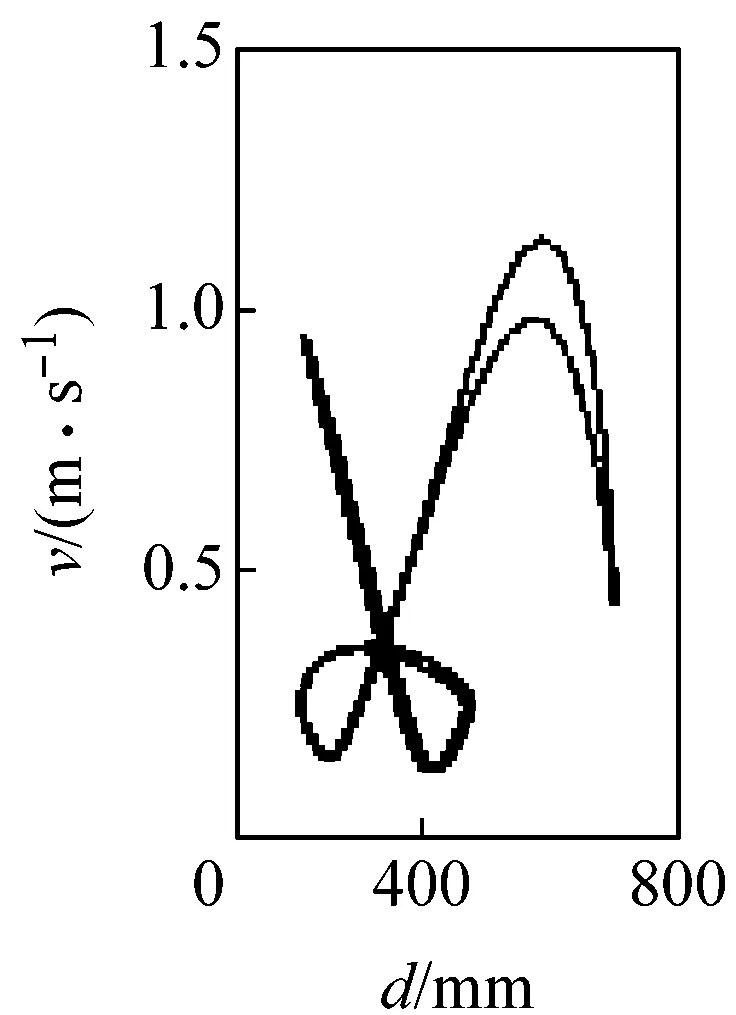
(a) c=0 mm

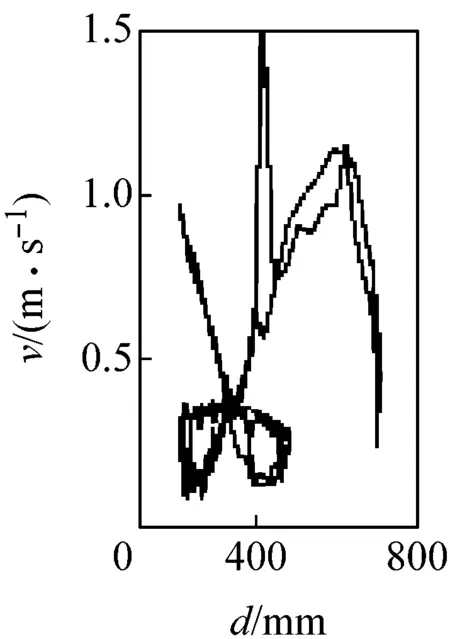
(c) c=0.20 mm

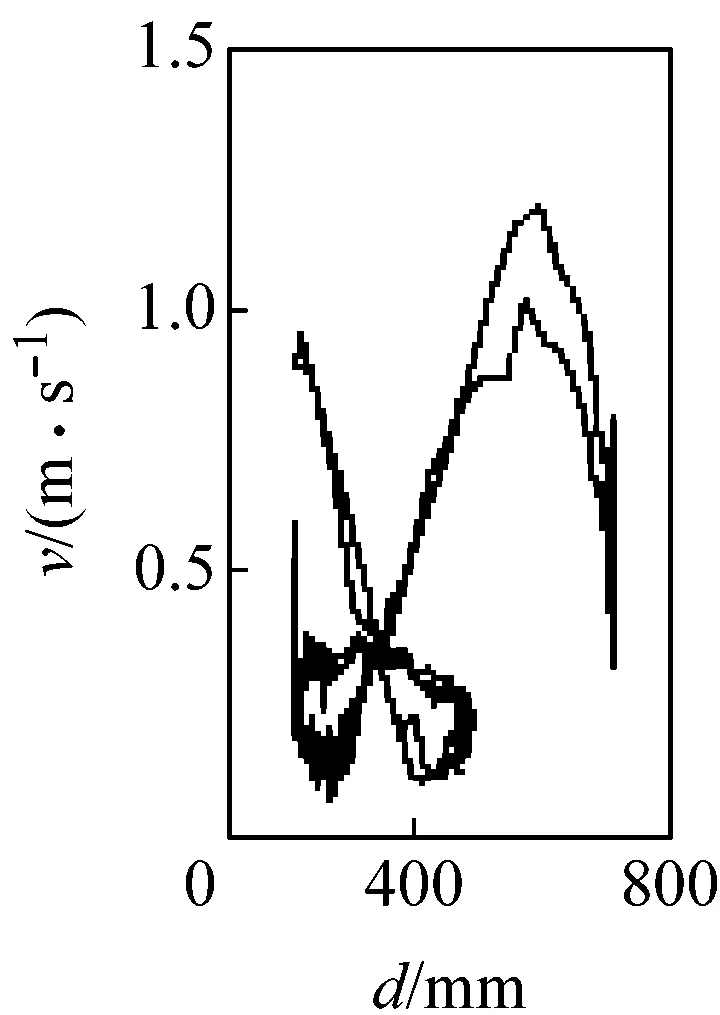
(d) c=0.30 mm

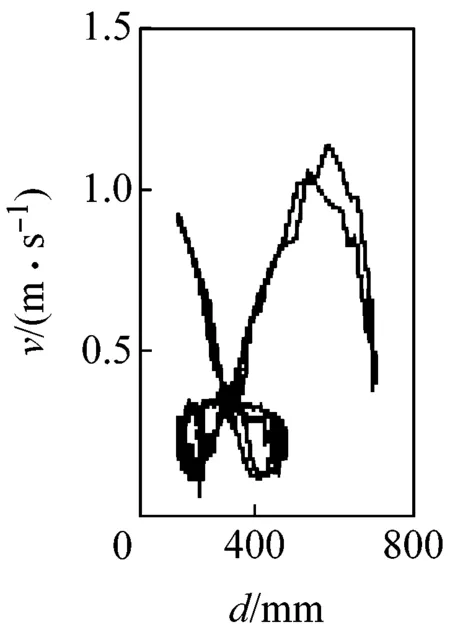
(f) c=0.50 mm

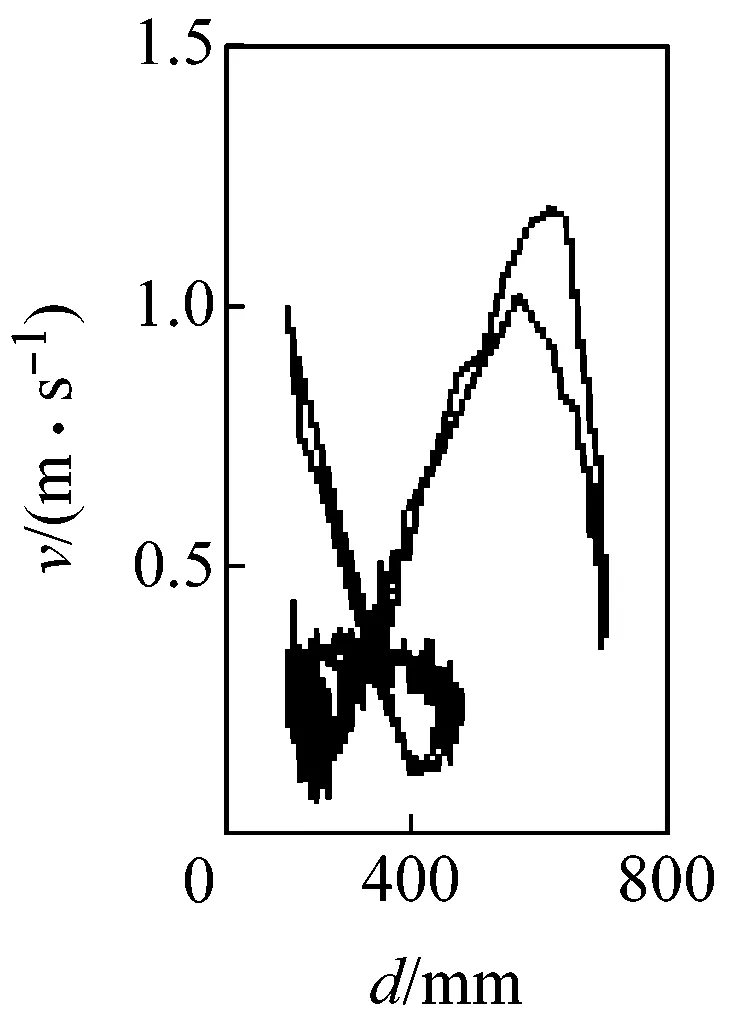
(g) c=0.75 mm

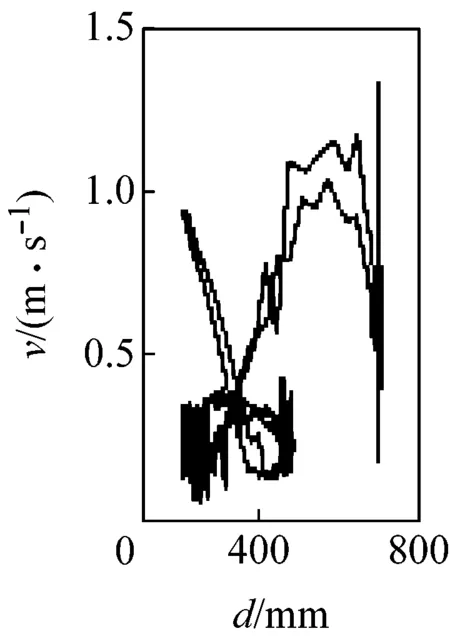
(h) c=1.00 mm

圖5G點速度相對于位移的相圖

Fig.5 Phase plane of velocity vs. displacement of G point

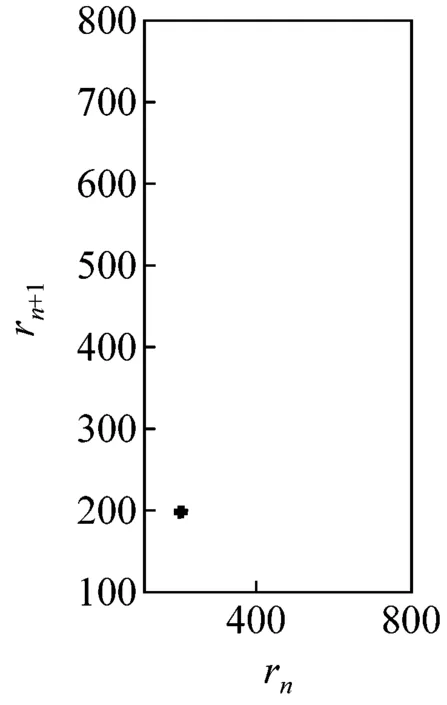
(a) c=0 mm

(b) c=0.10 mm

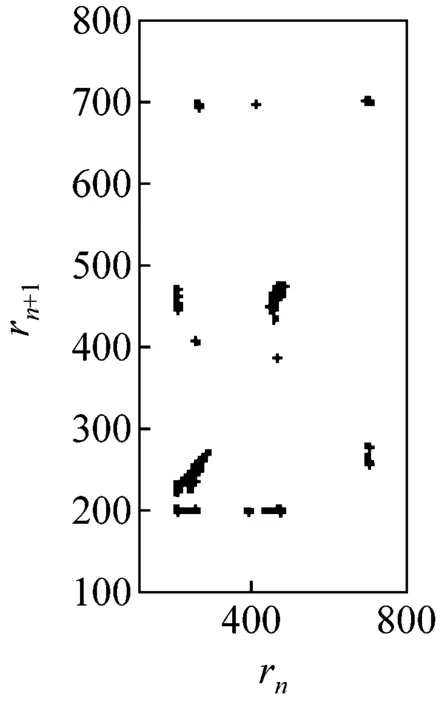
(c) c=0.20 mm

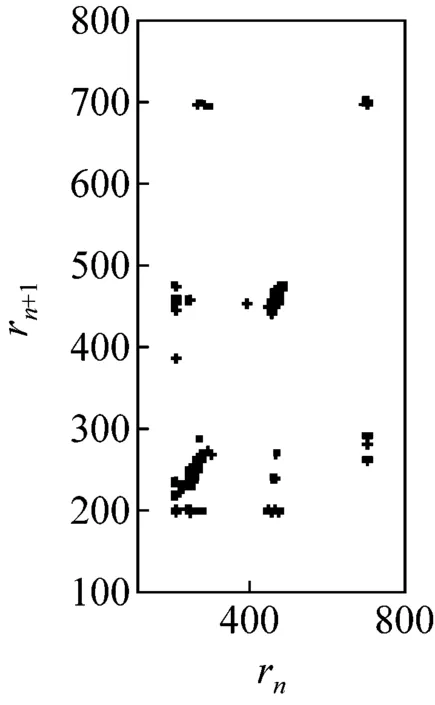
(d) c=0.30 mm

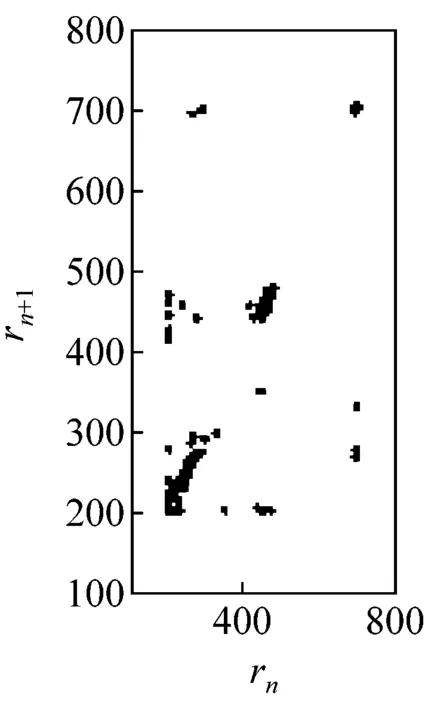
(f) c=0.50 mm

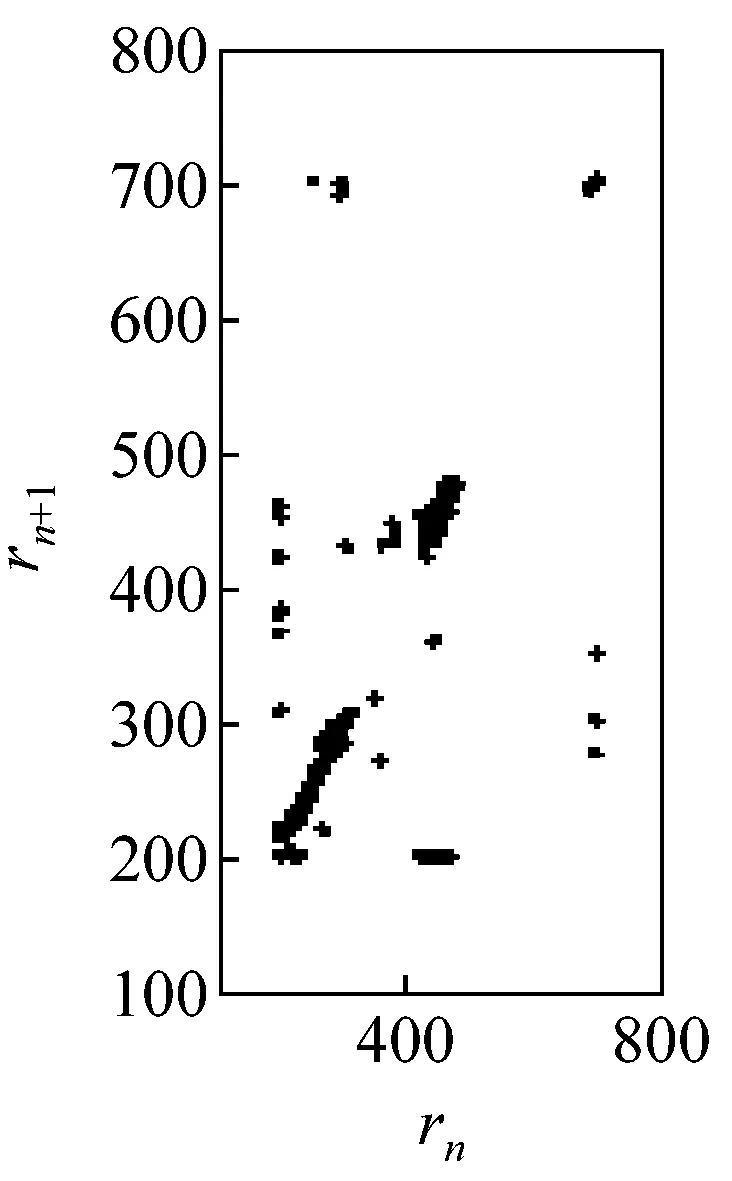
(g) c=0.75 mm

(h) c=1.00 mm

圖6龐加萊截面

Fig.6 The Poincaré section

3 結 語

本文以一個含間隙移動副的兩自由度平面連桿機構為研究對象，采用非線性連續接觸力模型建立了運動副間隙接觸碰撞約束，利用ADAMS對機構進行了數值仿真，研究了不同間隙值條件下，機構動力學行為和非線性特性。結果表明，運動副的間隙明顯改變了機構的動力學行為。隨著間隙值增大，機構運動速度波動和位移偏移隨之增加，運動精度和穩定性顯著降低；相圖和龐加萊截面顯示，機構動力學特性對初始間隙值非常敏感，并且隨著間隙增大，系統表現出從周期向混沌轉變的趨勢。

[1] 閻紹澤, 向吳維凱, 黃鐵球. 計及間隙的運動副和機械系統動力學的研究進展 [J]. 北京大學學報(自然科學版), 2016, 52(4):741-755.

[2] 王旭鵬, 劉更, 馬尚君. 含間隙運動副機構的動力學特性研究[J]. 振動與沖擊, 2016,35(7):110-115.

[3] 張晨旭, 楊曉東, 張偉. 含間隙齒輪傳動系統的非線性動力學特性的研究[J]. 動力學與控制學報, 2016, 14(2):115-121.

[4] DUBOWSKY S, FREUDENSTEIN F. Dynamic analysis of mechanical systems with clearances. Part 2: Dynamic response [J]. Journal of Engineering for Industry, 1971, 93(1):310-317.

[5] FLORES P, KOSHY C S, LANKARANI H M, et al. Numerical and experimental investigation on multibody systems with revolute clearance joints [J]. Nonlinear Dynamics, 2011, 65(4): 383-398.

[6] HOUFEK M, HOUFEK L. Bifurcation and chaos in couplings with clearance [J]. Advanced Materials Research, 2014, 936: 2120-2124.

[7] WANG Zhe, TIAN Qiang, HU Haiyan, et al. Nonlinear dynamics and chaotic control of a flexible multibody system with uncertain joint clearance [J]. Nonlinear Dynamics, 2016, 86(3): 1571-1597.

[8] STOENESCU E D, MARGHITU D B. Dynamic analysis of a planar rigid-link mechanism with rotating slider joint and clearance [J]. Journal of Sound and Vibration, 2003, 266(2): 394-404.

[9] KHEMILI I, ROMDHANE L. Dynamic analysis of a flexible slider-crank mechanism with clearance [J]. European Journal of Mechanics-A/Solids, 2008, 27(5): 882-898.

[10] DANIEL G B, CAVALCA K L. Analysis of the dynamics of a slider-crank mechanism with hydrodynamic lubrication in the connecting rod-slider joint clearance [J]. Mechanism and Machine Theory, 2011, 46(10): 1434-1452.

[11] DUPAC M, BEALE D G. Dynamic analysis of a flexible linkage mechanism with cracks and clearance [J]. Mechanism and Machine Theory, 2010, 45(12): 1909-1923.

[12] ZHENG Enlai，ZHU Rui，ZHU Sihong， et al. A study on dynamics of flexible multi-link mechanism including joints with clearance and lubrication for ultra-precision presses [J]. Nonlinear Dynamics, 2016, 83(1/2): 137-159.

[13] GU Pengyun, DUBOWSKY S, MAVROIDIS C. The design implications of chaotic and near-chaotic vibrations in machines [C]// Proceedings of the 1998 ASME Design Technical Conferences. Atlanta, GA：ASME，1998：1-11.

[14] SENEVIRATNE L D, EARLES S W E. Chaotic behavior exhibited during contact loss in a clearance joint of a four-bar mechanism [J]. Mechanism and Machine Theory, 1992, 27(3): 307-321.

[15] OLYAEI A A, GHAZAVI M R. Stabilizing slider-crank mechanism with clearance joints [J]. Mechanism and Machine Theory, 2012,53: 17-29.

[16] FLORES P. A parametric study on the dynamic response of planar multibody systems with multiple clearance joints [J]. Nonlinear dynamics, 2010, 61(4): 633-653.

[17] MUVENGEI O, KIHIU J, IKUA B. Numerical study of parametric effects on the dynamic response of planar multi-body systems with differently located frictionless revolute clearance joints [J]. Mechanism and Machine Theory, 2012,53: 30-49.

[18] TANG Yuanguang， CHANG Zongyu, DONG Xiaogang, et al. Nonlinear dynamics and analysis of a four-bar linkage with clearance [J]. Frontiers of Mechanical Engineering, 2013, 8(2): 160-168.

Influence of Slider Joint with Clearance on Nonlinear Dynamics of Planar Mechanism with Two Degrees of Freedom

WULijuan

(School of Mechanical Engineering, Shanghai Dianji University, Shanghai 201306，China)

In this study, the influence of joint clearance on the dynamic response of a mechanism with two degrees of freedom is investigated. A nonlinear dynamic model of clearance was built. The normal contact force was characterized by Hertz contact theory and an energy dissipation term. A tangential friction force was built based on Coulomb’s friction law. Dynamic simulation was carried out at different clearance sizes of the slider joint. The simulation results indicate that precision and stability of the system’s motion decrease as the clearance size increases. Furthermore, the phase plane and Poincaré section exhibit that the system has a tendency to move from periodic to chaotic as the clearance size increases.

slide joint clearance; dynamic response; nonlinear characteristic

2017 -09 -30

上海市網絡化制造與企業信息化重點實驗室開放課題資助(KT20150902)

午麗娟(1978-)，女，副教授，博士，主要研究方向為材料成型及控制，E-mail: wulj@sdju.edu.cn

2095-0020(2017)05 -0249-06

TH 122.1

A