耦合多螺旋槳滑流影響的低雷諾數機翼設計

王科雷， 周洲,*， 祝小平

1.西北工業大學 航空學院， 西安 710072 2.西北工業大學 無人機特種技術重點實驗室， 西安 710065

耦合多螺旋槳滑流影響的低雷諾數機翼設計

王科雷1,2， 周洲1,2,*， 祝小平2

1.西北工業大學 航空學院， 西安 710072 2.西北工業大學 無人機特種技術重點實驗室， 西安 710065

以某型手拋式太陽能無人機(UAV)模型為對象進行考慮多螺旋槳滑流影響的低雷諾數機翼平面形狀設計研究。首先，基于升力面理論發展了準定常求解多螺旋槳/機翼相互氣動干擾問題的渦格法(VLM)程序，并采用建立參考翼型氣動特性數據庫的形式發展了相關低雷諾數修正(LRC)方法；然后，通過對翼型、低雷諾數機翼及單螺旋槳/機翼算例的數值模擬及與相關實驗結果的對比，驗證了本文數值方法具備模擬低雷諾數復雜流動問題的可靠性及準確性；最后，對某型手拋式太陽能無人機簡化拉力多螺旋槳/機翼模型進行了直接優化設計及反設計，并通過具有較高精度的CFD準定常求解技術對優化結果進行了驗證。結果表明：以CFD方法計算結果為參考，本文渦格法程序及低雷諾數修正方法能夠準確高效地計算相關低雷諾數復雜流動問題；傳統未考慮多螺旋槳滑流影響的設計機翼在實際螺旋槳工作狀態下將偏離設計點，機翼氣動特性得不到提高；考慮螺旋槳滑流影響的優化設計方法能夠有效改善機翼阻力特性，相對應地，在設計狀態下優化機翼總阻力能夠降低19.52 counts。

手拋式太陽能無人機; 低雷諾數機翼; 多螺旋槳/機翼相互氣動干擾; 渦格法; 低雷諾數修正; 優化設計; 反設計

隨著近年來無人機(UAV)技術的快速發展，世界各國都在積極拓展民用無人機的應用范圍。無人機自身并沒有固定的標簽，它可以如同“互聯網+”一般被廣泛地應用到幾乎所有行業中，展現出極大的商業價值和應用前景。而中國地域廣闊，存在自然災害頻繁發生且種類繁多、邊境監控困難、海洋安全管控較弱等諸多問題，亟需依據不同領域或行業的具體需求從各個方面積極提高自身無人機的研發能力。

從邊境巡邏的角度出發，在無人機平臺安全、可靠的基礎上還需要具備2項能力：① 簡單、易操作的起降模式；② 足夠大的航程和航時。此時手拋式固定翼太陽能無人機[1]就顯示出其他種類無人機無法比擬的巨大優勢。然而，由于此類無人機尺度較小，且飛行速度較低，其低雷諾數復雜流動特征[2-4]極為顯著，數值模擬難度及氣動設計難度均相對常規飛行器較大。

作為典型的螺旋槳類飛行器，將螺旋槳滑流影響納入無人機氣動設計階段將顯得尤為重要。自1986年Kroo[5]首次提出在螺旋槳旋轉的真實狀態下進行機翼設計相比干凈機翼設計更具意義以來，Veldhuis[6-8]及Rakshith[9]等相繼對螺旋槳/機翼構型各種布局參數進行了氣動影響數值研究及氣動布局設計研究；喬宇航等[10]基于升力線理論，通過對機翼幾何扭轉分布的控制達到了降低機翼誘導阻力的目的；徐家寬等[11]采用基于雷諾平均Navier-Stokes(Reynolds Averaged Navier-Stokes, RANS)方程的多重參考坐標系(Multi Reference Frame, MRF)方法[12-13]對某型運輸機機翼局部區域剖面翼型進行了考慮螺旋槳滑流影響的氣動優化設計，并且采用Kriging代理模型[14-15]進一步減少計算量，提高設計效率。

盡管國內外眾多學者已經針對螺旋槳/機體一體化設計問題進行了大量研究，但其氣動設計過程主要是在常規雷諾數狀態下進行，而且受到計算效率的限制，其所采用的數值計算方法大多是以無黏近似求解方法為主，這對于太陽能無人機氣動設計所處的低雷諾數強黏性環境顯然行不通。另外，就目前而言，低雷諾數流動本身的數值計算便已經較為困難，而當引入多個螺旋槳滑流氣動干擾后其數值計算更將是難上加難，因此常規的太陽能無人機設計過程[16-18]仍未將動力系統的氣動影響考慮在內。總的來說，低雷諾數流動數值模擬方法精度和效率之間的矛盾是制約太陽能無人機螺旋槳/機翼一體化氣動設計發展的主要因素。

基于以上考慮，本文首先發展了一套準定常求解多(拉力)螺旋槳/機翼相互氣動干擾問題的渦格法(Vortex Lattice Method, VLM)程序，并以建立參考翼型氣動特性數據庫的形式發展了相關低雷諾數修正(Low Reynolds Correction, LRC)方法；然后以CFD方法作為參考，通過對低雷諾數翼型及機翼算例的數值模擬開展了數值方法的驗證及評價；最后基于某型手拋式太陽能無人機模型開展了低雷諾數機翼平面形狀優化設計研究，并基于CFD方法對設計結果進行了驗證及分析。

需要說明的是，本文渦格法及相關低雷諾數修正方法程序均采用FORTRAN語言編寫，氣動優化設計方面采用iSIGHT商業軟件實現，而CFD計算方面則采用Fluent商業軟件實現。

1 數值方法

1.1 渦格法

渦格法是基于薄物體的假定簡化，在流體無旋、無黏、不可壓縮的無界流域內，使用離散的源匯、渦和偶極子等奇點組合來模擬流動現象，其數值計算較為簡便，應用極為廣泛。

面對多個螺旋槳加機翼的布局形式，采用馬蹄渦和源的奇點組合，共5個渦系形成離散數學模型：螺旋槳槳葉渦系、螺旋槳尾跡渦系、機翼翼面渦系、機翼翼面源系及機翼尾跡渦系。其中，隨著機翼模型的確定，機翼翼面渦系及尾跡渦系中渦格節點及控制點的空間位置始終保持不變，而各螺旋槳槳葉及尾跡渦系渦格節點及控制點的瞬時空間位置則由輸入文件中螺旋槳安裝位置、螺旋槳轉速及計算時刻所確定。

渦格法離散數學模型中，機翼翼面區域內展向劃分50格，并在機翼翼尖和螺旋槳下游區域進行局部加密，而弦向則按余弦函數劃分40格，共計2 000個渦格；螺旋槳模型僅包含槳葉而忽略輪轂，各槳葉葉面區域展向均勻劃分25格，弦向均勻劃分40格，共計1 000個渦格；整個計算模型總渦格量為(1 000×nblade×npro+2 000)個，nblade為單個螺旋槳的槳葉數目，npro為計算模型所采用的螺旋槳數目。

另外，考慮到渦格法旨在進行氣動特性快速計算，在其數學建模過程中主要進行了2項簡化：① Michael和Brian[19]將機翼和螺旋槳的自由尾跡形式與預定尾跡形式進行了對比，計算表明基于2種尾跡形式的升力、阻力計算結果誤差不超過0.1%，因此本文渦格法程序中采用預定尾跡的形式以提高計算效率。其中，機翼尾跡渦系采用10倍弦長的考慮機翼展向兩端尾渦卷曲的二次拋物線型固定尾跡渦模型，而螺旋槳尾跡渦系則近似采用5倍弦長的由槳葉后緣各面元節點帶出的螺旋面型預定尾跡渦模型。② Rangwalla和Wilson[20]提出，為了符合實際流動問題中機翼表面不可穿透的條件，近似地將與機翼實體相交的螺旋槳尾跡面元進行“消除”(Wake Snipping)處理，同時該處理方式在對復雜外形的非定常勢流求解迭代過程中能夠有效提高數值計算的效率和穩定性，因此本文渦格法程序中也采用同樣的對螺旋槳尾跡面元的“消除”處理。

螺旋槳與機翼之間的相互氣動干擾通過各不同渦系之間的速度相互誘導來實現。將螺旋槳旋轉周期劃分為數個瞬時狀態，當某一時刻螺旋槳瞬時相位角即槳葉位置確定時，各渦系之間誘導速度影響系數矩陣也可以通過Biot-Savart法則確定，基于物面不可穿透條件解得當前時刻各渦系內各面元渦強度，進而解得瞬時氣動力系數，最終以一個周期內各瞬時氣動力系數之和求平均的方法獲得準定常氣動特性參數。

1.2 低雷諾數修正方法

目前有關低雷諾數復雜流動數值計算及修正的方法發展仍相對不夠成熟，大部分研究[21-22]所發展的低雷諾數修正方法主要是依據經驗公式對數值結果直接進行修正，缺乏物理內涵，這對簡單線性問題可能還較為適用，但當應用于多螺旋槳/機翼相互氣動干擾的低雷諾數復雜流動問題時其修正精度及可靠性均無法得到保證。

因此，本文由物理層面出發，對低雷諾數平直機翼復雜繞流問題作出2項簡化：① 將低雷諾數機翼繞流問題簡化為機翼無黏繞流問題與低雷諾數黏性影響的疊加，也即在渦格法數值計算基礎上假設低雷諾數黏性影響是直接作用于各渦格內的渦線段強度；② 借鑒葉素理論[23]基本原理及思想，將機翼型阻的估算問題簡化為各展向位置當地迎角下的低雷諾數翼型阻力積分問題。基于以上2項簡化，本文發展的低雷諾數修正方法具體步驟可以概括如下：

步驟1建立當前低雷諾數條件下的翼型氣動特性參考數據庫。分別采用無黏求解方法(求解歐拉方程)和黏性求解方法(求解RANS方程)計算出當前雷諾數條件不同迎角下的機翼剖面翼型氣動力參數，將2種情況下翼型計算升力的比值作為低雷諾數條件對翼型環量的影響系數λ，建立當前雷諾數Re條件不同計算迎角α下的黏性影響系數Re-α-λ數據庫。另外，基于黏性計算結果建立當前雷諾數條件下的翼型計算升阻力系數Re-cl-cd數據庫。

步驟2在渦格法計算過程中，基于機翼不同展向位置的當地來流迎角，參考Re-α-λ數據庫選取對應黏性影響系數λ對該區域所有弦向渦格中渦線段強度進行修正，之后繼續求解以得出修正后的升力系數CL及誘導阻力系數CDi。另外，考慮到：① 機翼翼尖附近區域氣流下洗作用強度極大，造成了該區域翼段所產生升力在機翼整體升力中僅為一小量，對其進行修正與否對機翼整體氣動特性計算結果影響不大；② 盡管機翼翼尖仍處于低雷諾數流動中，但其繞流流動特征是以翼尖渦形式為主，且流動形態極為復雜，難以直接建立相關數據庫以進行低雷諾數修正。因此，在低雷諾數修正程序編寫中對機翼翼尖附近區域內渦格的渦線段強度將不作任何修正處理，且將該區域范圍初步定義為由翼尖向內0.5倍弦長的長方形區域。

步驟3基于沿機翼展向分布的升力系數計算值，參考Re-cl-cd數據庫對應求出不同展向位置的各剖面翼型阻力系數，則機翼總型阻系數CDp可以按式(1)求解：

(1)

式中：b為機翼展長；c為弦長；y為機翼展向位置；Sw為機翼總面積。最終機翼總阻力系數CD即為機翼誘導阻力系數與機翼型阻系數之和。

另一方面，由于螺旋槳沿徑向的扭轉角、槳葉寬度以及槳葉剖面翼型變化較大，流動形態極為復雜，且隨著螺旋槳的尺寸及轉速等改變時其各剖面的當地迎角、當地雷諾數等亦改變較大，若仍采用上述建立參考數據庫的方法來進行修正將顯得不切實際。考慮到本文主要目的是將電推進系統(螺旋槳)滑流誘導的氣動影響納入機翼優化設計過程中，而并不著重強調對螺旋槳氣動及流動特性的準確計算，因此，在低雷諾數修正程序編寫中對螺旋槳模型中弧面上渦格的渦線段強度亦將不作任何修正處理。

1.3 CFD方法

采用基于結構-非結構混合網格技術耦合轉捩模型準定常求解RANS方程的MRF方法對多螺旋槳/機翼氣動干擾問題進行數值模擬。空間離散采用二階迎風MUSCL(Monotone Upstream-centered Scheme for Conservation Laws)插值的Roe格式，時間離散與推進則采用隱式AF(Approximate Factorization)方法。

1) MRF模型方法

MRF模型方法是一種對螺旋槳滑流進行準定常數值模擬的數學方法，相比于過分耗費計算資源的非定常求解方法，MRF模型方法在更加節省計算資源的同時仍能獲得較高的數值模擬精度，在定軸旋轉體的氣動計算中應用較為廣泛[12-13]。

MRF模型方法主要思想是：通過在各螺旋槳周圍建立一個規則封閉圓柱流動區域來模擬螺旋槳的旋轉運動。建立與螺旋槳具有相同旋轉運動方式的旋轉坐標系，通過相應的數學轉換以及旋轉區域與非旋轉區域的數據插值傳遞，實現在靜態網格下的包含旋轉氣流的流場數值模擬。其旋轉坐標系下積分形式控制方程為

(2)

式中：t、V和A分別為時間項、流體微元控制體和圍成控制體的閉曲面；n為曲面或曲線的單位法向量；Q、H、HV和G分別為守恒變量、無黏通量項、黏性通量項和坐標轉換的添加源項，其具體求解公式可參考文獻[12]。

2) 結構-非結構混合網格技術

與MRF模型方法的遠場靜止流動區域及圓柱旋轉流動區域相對應，將計算網格劃分為靜止域網格和運動域網格。針對靜止區域劃分結構化網格以減小網格總量，節約計算時間；針對運動區域，由于螺旋槳槳葉在徑向位置具有不同的葉素安裝角，槳葉高度扭轉，幾何外形比較復雜，劃分非結構化網格可以在保證計算精度的同時降低槳葉的網格難度，提高網格生成效率。

圖1所示為螺旋槳/機翼構型混合網格結構。機翼所處的非旋轉區域結構化網格近壁面網格y+約為0.5，網格量始終保持在600萬左右。而螺旋槳所處圓柱形旋轉區域非結構化網格近壁面網格y+約為1.5，網格量始終保持為200萬左右。

圖1 螺旋槳/機翼構型混合網格結構示意圖Fig.1 Schematic of hybrid grids structure of propeller/wing configuration

3)k-kL-ω轉捩模型

通常，巡航狀態下的太陽能無人機繞流問題是處于104～105量級的低雷諾數范疇，在數值計算中必須考慮層流轉捩的問題。因此，采用Walters等[24-25]以及Volino[26]提出的基于局部變量“層流動能”的k-kL-ω轉捩模型進行求解，其輸運方程組可寫為

(3)

(4)

(5)

湍流動能及層流動能生成項及近壁面耗散項表達式分別為

(6)

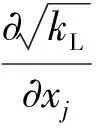
(7)

式中：x為坐標軸系，其下標i、j表示各軸系方向；k為動能；ν為黏性系數；下標T和L分別表示湍流和層流；下標s和l分別表示小尺度和大尺度；ω為湍流頻率；αT為湍流標量擴散率；S為張力率梯度；R和RNAT分別為由旁路轉捩和自然轉捩引起的湍流產生項；其相關變量及相關參數具體值可參考文獻[24]。

2 數值方法驗證及評價

本文基于渦格法發展低雷諾數修正方法(統稱為VLM-LRC方法)的主要目的是為了在低雷諾數飛行器數值優化過程中取代計算效率相對較低的CFD方法，在提供足夠計算精度的同時進一步提高設計效率。考慮到本文所發展低雷諾數修正方法的關鍵環節為相關參考數據庫的建立，因此該參考數據庫的準確性及可靠性就顯得尤為重要，而這些均依賴于所采用數值模擬方法求解低雷諾數問題的計算能力。因此，本節將首先對CFD方法數值模擬低雷諾數翼型繞流問題的計算精度進行驗證，之后以CFD方法計算結果為參考來對VLM-LRC方法計算精度及效率進行驗證和評價。主要包含以下3部分內容：

1) 通過低雷諾數條件下翼型算例驗證CFD方法具備精確描述低雷諾數復雜流動特性的能力。

2) 通過低雷諾數機翼及單螺旋槳/機翼算例驗證VLM-LRC方法在低雷諾數復雜流動問題求解方面具備較高的計算精度。

3) 通過對CFD方法與VLM-LRC方法數值計算耗時的對比，證明VLM-LRC方法在獲得足夠計算精度的前提下能夠有效提高計算效率。

2.1 CFD方法驗證

[27]中相關實驗條件及結果，對NACA633-018翼型進行數值模擬。選取計算狀態為：遠場來流速度V∞=15 m/s，來流湍流度Tu∞=0.25%，弦長雷諾數Rec=3.0×105。圖2給出了不同迎角下翼型計算壓力系數Cp分布與實驗結果對比。

圖2 翼型壓力系數分布對比 Fig.2 Comparison of airfoil pressure coefficient distribution

由圖2可以看出，本文CFD方法在不同迎角下翼型壓力分布計算結果與實驗值吻合很好，k-kL-ω轉捩模型對翼型表面壓力平臺區域預測精度較高，也即對翼型繞流流場中層流分離、轉捩及湍流再附位置的預測精度較高。這也驗證了本文CFD方法精確描述低雷諾數復雜流動的有效性，為下文計算分析提供可靠的氣動特性計算基礎。

2.2 VLM-LRC方法驗證

參考文獻[28]中相關實驗條件及結果，對展弦比為8的FX 63-137低雷諾數平直機翼模型(Wing)進行數值模擬。選取計算狀態為：遠場來流速度V∞=30 m/s，飛行高度H=20 km，來流湍流度Tu∞=0.1%，弦長雷諾數Rec=3.0×105。另外，在該低雷諾數機翼的基礎上再構造單螺旋槳/機翼模型(Spro)進行數值模擬，其中螺旋槳模型采用直徑為1.2 m的某型雙葉螺旋槳X1，以0° 安裝角安裝在機翼中心正前方0.8 m處，旋轉方向為順氣流逆時針方向，螺旋槳轉速為2 500 r/min。

圖3為分別采用CFD方法及VLM-LRC方法計算得到的各構型機翼氣動力數值計算結果與實驗結果對比。圖4為2° 迎角下2種構型機翼展向升力系數分布對比。其中，整個機翼沿展向平均劃分為40份，而黑色箭頭方向表示螺旋槳誘導下氣流上洗、下洗特征。由于本文更加側重于考慮機翼不同展向位置各等展長翼段升力對機翼整體升力的貢獻量，因此各翼段升力系數將始終采用機翼總面積作為參考面積進行計算，而下文機翼沿展向分布的升力計算方式亦與此處相同。

圖3 機翼氣動特性數值計算與實驗結果對比Fig.3 Comparison of wing aerodynamic performance between numerical and experimental results

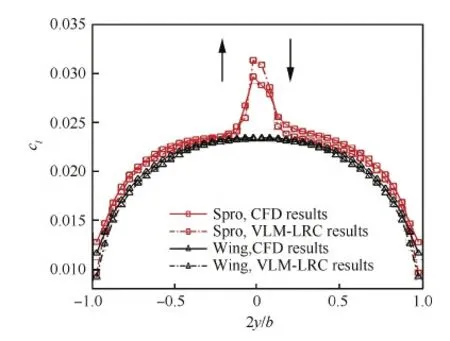
圖4 2° 迎角下機翼展向升力系數分布對比 Fig.4 Comparison of wing span-wise lift coefficient distribution (α=2°)

由圖3可以看出，采用CFD方法計算得到的干凈機翼氣動力系數與實驗數據符合良好，僅在大迎角條件下相對誤差較大；采用VLM-LRC方法計算得到的2種構型氣動力系數均與CFD方法計算結果吻合較好，但VLM-LRC方法計算升、阻力曲線隨迎角的增長率相對較小，全迎角范圍內2種數值方法計算結果之間相對誤差均不超過6.5%；當引入螺旋槳滑流影響時，機翼升、阻力均有所增大，而VLM-LRC方法及CFD方法計算結果基本一致，所得到的氣動力系數增加量亦基本相同。

由圖4可以看出，VLM-LRC方法計算得到的2種構型機翼展向升力分布曲線均與CFD方法計算結果吻合良好，僅在螺旋槳中心輪轂下游區域以及翼尖附近區域的計算升力差別較大，這可能與渦格法對螺旋槳幾何模型的簡化以及低雷諾數修正方法對螺旋槳及機翼渦格強度的修正處理等均有關系，但整體上并不影響VLM-LRC方法計算結果與CFD方法計算結果之間的一致性。另外，當前狀態下螺旋槳對遠場來流的加速效應顯著強于旋轉效應，螺旋槳下游機翼翼段當地雷諾數相對增大，機翼剖面升力系數均顯著增高，同時由于旋轉效應始終存在，機翼翼段上洗側剖面翼型升力相對增量大于下洗側剖面翼型升力增量。

2.3 VLM-LRC方法評價

本文使用Fluent商業軟件建立Rec=3.0×105條件下的FX 63-137低雷諾數翼型氣動特性參考數據庫，耗時約3 h。表1為分別使用VLM-LRC方法和CFD方法完成該雷諾數條件下干凈機翼算例及單螺旋槳/機翼算例所需要的計算模型渦格量或網格量，以及各自對應消耗的機時(所有計算均在同一臺4核8線程計算機中進行)。其中，CFD方法計算耗時是在達到與VLM-LRC方法計算結果相同精度時所耗費的時間。可以看出，在達到相同計算精度的前提下，VLM-LRC方法計算效率相對CFD方法顯著較高。

表1 氣動性能計算消耗時間Table 1 Aerodynamic performance calculated time

3 太陽能無人機機翼平面形狀設計

通過2.2節研究可以看出，利用螺旋槳滑流影響來降低機翼誘導阻力具有一定的可能性與可行性。螺旋槳滑流影響下的機翼升力明顯增大，也就是說，在提供相同升力的情況下，考慮螺旋槳滑流影響的機翼環量需求更低，繼而其誘導阻力也會進一步降低。因此，本節將以機翼展向升力分布接近理論橢圓形曲線(對應誘導阻力最小)為目標進行機翼平面形狀設計研究。基于VLM-LRC方法針對某型手拋式太陽能無人機采用直接優化設計與反設計相結合的方法，分別對螺旋槳停機以及螺旋槳工作2種情況下的機翼平面形狀進行優化設計，并采用CFD方法對優化設計結果進行驗證、比較及分析。

3.1 手拋式太陽能無人機

圖5(a)給出了某型手拋式太陽能無人機構型示意圖。該無人機采用了雙尾撐和倒V尾的布局形式，機翼采用FX 63-137平直機翼，弦長0.3 m，展長4.5 m，2個螺旋槳均為直徑0.3 m的X1螺旋槳，以0° 安裝角對稱安裝在機翼兩側正前方0.2 m的位置，螺旋槳間距為1.8 m，左、右螺旋槳分別沿順氣流方向逆時針、順時針旋轉。該無人機巡航(設計)狀態選為：遠場來流速度V∞=15 m/s，飛行高度H=500 m，機翼弦長雷諾數Rec=3.0×105，螺旋槳工作轉速為4 000 r/min。

為提高計算及設計效率(見圖5(b))，對該無人機模型進行簡化，忽略機身、吊艙以及倒V尾的影響，且僅針對螺旋槳同步旋轉時其滑流影響下的機翼平面形狀進行優化設計。

圖5 手拋式太陽能無人機構型示意圖Fig.5 Schematic of hand-throw solar-powered unmanned aerial vehicle

3.2 氣動優化設計

圖6為相關的低雷諾數機翼平面形狀具體優化設計流程，該研究內容共由2輪設計完成：第1輪直接優化設計，以及第2輪反設計。

圖6 優化設計流程Fig.6 Flowchart of optimization design process

3.2.1 直接優化設計

在直接優化設計過程中，首先，結合實際工程需求，以太陽能無人機機翼面積，也即太陽能電池鋪設面積不變為約束條件，對機翼平面形狀進行參數化建模，建模過程中采用三次B樣條曲線[29-30]對機翼后緣(Trailing Edge, TE)邊界形狀進行控制，沿單側機翼展向共選取6個控制點，各控制點參數設計空間為(-3.0，2.0)，當控制前后機翼面積變化量ΔSw≤0.001 m2時，即可認為滿足機翼面積不變的約束條件；然后，采用VLM-LRC方法直接并行求解當前模型在0° 和2° 迎角時的機翼氣動力系數，采用線性插值方法計算出CL=0.9時的機翼阻力系數CD，同時計算出2° 迎角時優化機翼展向升力分布曲線與理論橢圓形分布曲線的均方根誤差ε；最后，采用NSGA-II遺傳算法[31-32]為搜索器進行直接多目標數值優化，其中種群個體數設定為12，遺傳代數設定為20，交叉率設定為0.9，變異率設定為0.5。

直接優化目標設定為：在太陽能無人機巡航狀態提供升力系數CL=0.9的約束條件下，獲得最優CD及ε。該優化設計問題可以表示為

Objective function:minJ=ω1CD+ω2ε

式中：ω1和ω2為權重系數，取值均為0.5。

相比于傳統多目標優化算法，NSGA-II遺傳算法運行一次即可獲得多個Pareto最優解，且其運算效率高，解集亦具有良好的分布性，特別是對目標個數較少的問題有很好的表現。圖7給出了

圖7 NSGA-II遺傳算法優化搜索迭代過程 Fig.7 Iteration history of optimization search by NSGA-II genetic algorithm

本文機翼平面形狀尋優迭代歷程。可以看出，經過優化設計系統的優化搜索，可以得到阻力特性明顯改善的優化結果。

3.2.2 反設計

在直接優化設計結果的基礎上進一步對機翼誘導阻力系數進行反設計，將機翼展向升力分布按理論橢圓形曲線分布為目標，以機翼展向升力分布曲線與理論橢圓形曲線的逼近程度，也即均方根誤差ε的大小作為衡量標準，對機翼弦長分布進行修正設計。

首先，判斷當前模型機翼展向升力分布曲線與理論橢圓形曲線之間的均方根誤差ε是否滿足設計終止條件(ε≤0.005)，若是，則輸出設計結果，若否，則對當前模型機翼各控制點處截面升力系數與最優橢圓形理論值之間的關系進行判斷及分析，基于該關系對各控制點參數進行步長為 0.1 的余量修正；然后，更新計算模型，如此反復；最后，設計出滿足要求的機翼平面形狀。

3.3 優化結果分析

圖8為優化前后機翼平面形狀對比。為了便于區分，將原始機翼、螺旋槳停機狀態優化機翼以及螺旋槳工作狀態優化機翼分別命名為Original wing、W-optimal wing及P-optimal wing以示區分。可以看出，當不考慮螺旋槳滑流影響時，優化機翼平面形狀呈現出類橢圓形特征，翼尖區域機翼弦長顯著減小；而當考慮螺旋槳滑流影響時，整個機翼后緣形狀呈波浪形，翼尖區域和螺旋槳下游區域機翼弦長均顯著減小。

圖9為2° 迎角下3種機翼在螺旋槳停機及工作狀態下的展向升力系數分布曲線與理論橢圓形升力系數分布曲線的對比。其中，各機翼沿展向被均分為50份，且螺旋槳靠近機翼對稱面的一側為上洗側，靠近機翼翼尖的一側為下洗側。考慮到本文引入理論橢圓形升力系數分布曲線的主要目的是為了通過與計算升力系數分布曲線之間的對比為后續機翼設計提供指導，并不具備實際意義，因此在橢圓形曲線構建過程中不考慮曲線與x軸所圍成的面積，也即橢圓形機翼理論升力與當前機翼計算升力一致，其半短軸取值始終為1.0，半長軸取值則始終為當前機翼中心截面翼型計算升力系數。

圖8 優化前后機翼平面形狀對比Fig.8 Comparison of wing planform between before and after optimization

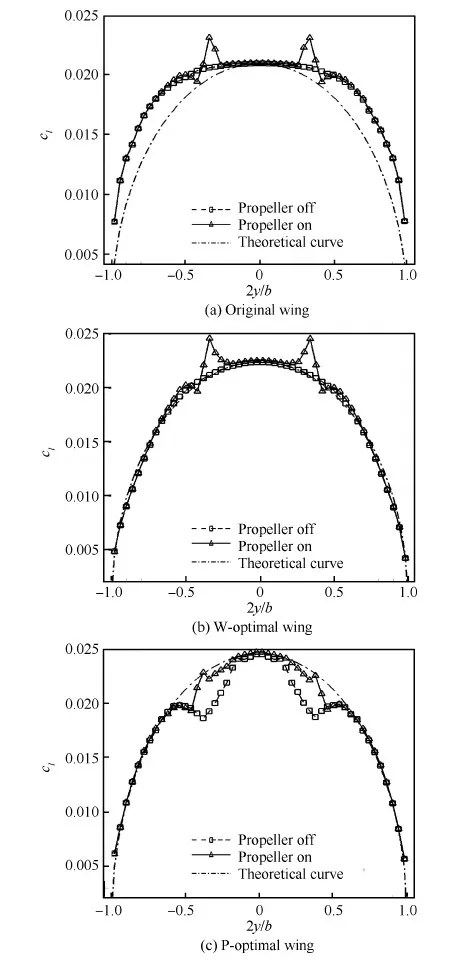
圖9 2° 迎角下3種機翼展向升力系數分布對比Fig.9 Comparison of span-wise lift coefficient distribution among three wings (α=2°)

由圖9可以看出：① 螺旋槳滑流主要改變其對應下游有限區域內的機翼計算升力分布，其對機翼翼尖及翼根處的氣動力分布幾乎沒有任何影響，同時當前狀態下螺旋槳對遠場來流的旋轉效應相對更強，左右螺旋槳下游機翼展向升力分布形態均呈現出典型的氣流上洗側升力增大、下洗側升力減小特征。② 當螺旋槳停機時，原始機翼沿展向的升力系數分布曲線與橢圓形理論曲線差別顯著，而在螺旋槳停機狀態下進行設計的優化機翼“W-optimal wing”沿展向的計算升力系數分布曲線與橢圓形理論曲線幾乎完全吻合，而優化機翼“P-optimal wing”沿展向升力系數分布曲線則與其呈波浪形分布的機翼弦長相對應，在機翼弦長顯著減小的螺旋槳下游區域內計算升力系數相對理論亦較小，此時原始機翼、優化機翼“W-optimal wing”以及優化機翼“P-optimal wing”3種機翼展向升力系數分布曲線與理論橢圓形分布曲線的均方根誤差依次為0.024 2、0.003 6和0.013 3。③ 當螺旋槳工作時，螺旋槳滑流的加速作用十分顯著，3種機翼在各自螺旋槳下游區域均與螺旋槳旋轉方向相對應地呈現出較為顯著的氣流上洗及下洗特征，原始機翼及優化機翼“W-optimal wing”展向升力分布均方根誤差亦顯著增大，而優化機翼“P-optimal wing”由于其呈波浪形分布的機翼弦長能夠與螺旋槳滑流影響形成有效互補，其沿展向的計算升力系數分布曲線與橢圓形理論曲線吻合相對較好，此時3種機翼展向升力系數分布曲線與理論橢圓形分布曲線的均方根誤差依次為0.027 4、0.007 1 和0.004 7。

表2優化前后機翼阻力系數對比(CL=0.9)

Table2Comparisonofwingdragcoefficientsbeforeandafteroptimization(CL=0.9)

PropellerWingΔCDi/countΔCDp/countΔCD/countΔCD/%OffOriginal193．0143．0336．0W?optimal172．2148．4320．6-4．58P?optimal184．4141．3325．7-3．06OnOriginal190．0154．3344．3W?optimal186．4174．3360．7+4．76P?optimal176．6150．0326．6-5．14

表2為螺旋槳停機及工作2種狀態下在達到設計升力系數CL=0.9時的優化前后機翼計算阻力系數(1 count=10-4)對比。其中，總阻力系數變化百分比均是以相同狀態下的原始機翼總阻力為參考進行計算。

可以看出：① 在螺旋槳工作狀態下，原始機翼誘導阻力系數相對螺旋槳停機狀態稍有減小，這表明與翼尖渦方向相反的螺旋槳滑流可以在一定程度上促使機翼誘導阻力降低，但機翼型阻相對顯著增大，整體上機翼總阻力計算值增大達8.3 counts。② 在螺旋槳停機狀態下，優化機翼“W-optimal wing”計算誘導阻力相對同狀態原始機翼減小達20.8 counts，但計算型阻相對增加約5.4 counts，計算總阻力相對減小4.58%，這表明以機翼展向升力分布形態為衡量標準的設計思路可行有效。但在螺旋槳工作狀態下，優化機翼“W-optimal wing”并沒有表現出如螺旋槳停機狀態一般的優秀特性，其誘導阻力相對同狀態原始機翼僅有3.6 counts的減小量，而由于螺旋槳下游機翼弦長的增加，對應其剖面升力系數有所增加，從而導致機翼型阻相對顯著增大，機翼總阻力亦顯著增大達4.76%。也就是說，在螺旋槳工作狀態下，該優化機翼阻力特性相比原始機翼反而有所惡化。③ 在螺旋槳停機狀態下，優化機翼“P-optimal wing”計算誘導阻力及型阻均相對同狀態原始機翼稍有減小，最終機翼總阻力相對減小3.06%。而在螺旋槳工作狀態下，優化機翼“P-optimal wing”計算誘導阻力減小量顯著增大至13.4 counts，同時由于螺旋槳下游機翼弦長的減小，其計算型阻亦相對稍有減小，最終優化機翼“P-optimal wing”計算總阻力相對減小達17.7 counts，占同狀態原始機翼總阻力的5.14%。

由此可見，對于螺旋槳類飛機而言，傳統未考慮螺旋槳滑流影響而僅針對干凈機翼進行氣動設計的思路在實際應用中存在較嚴重問題，而考慮實際工作狀態螺旋槳滑流影響下的機翼氣動優化設計顯然更具有意義。

3.4 優化結果驗證

考慮到實際工程中，三次曲線形狀的機翼后緣邊界將為機翼結構的設計、加工與制造，以及機翼舵面的設計、安裝與操縱等帶來困難。本文在優化機翼實體建模過程中，針對性地對機翼后緣形狀進行了修正——利用若干條直線段代替曲線邊界。圖10為優化機翼“P-optimal wing”后緣修正前后的平面形狀對比。圖中：左側為B樣條曲線型后緣模型，右側為修正后的折線型后緣模型。

圖11為采用CFD方法計算得到的實際螺旋槳工作狀態下的優化前后幾種機翼升阻特性計算結果對比。圖中：B-spline和Polyline分別代表曲線型后緣和折線型后緣的優化機翼。

由圖11可以看出：① 折線型后緣與曲線型后緣對機翼氣動力結果影響并不明顯，全計算迎角范圍內二者之間的升阻力相對誤差始終在0.3% 以內。② 相對于原始機翼，2種優化機翼在各迎角下的計算升阻力均有所減小，而在設計狀態機翼CL=0.9時，優化機翼“W-optimal wing”阻力系數相對原始機翼增大約20.13 counts，占原始機翼總阻力的6.29%，而優化機翼“P-optimal wing”阻力系數則相對減小約19.52 counts，占原始機翼總阻力的6.10%。

由此可見，CFD方法計算結果及氣動力變化趨勢與VLM-LRC方法計算結果較為一致，這表明本文基于VLM-LRC方法發展的耦合螺旋槳滑流影響的機翼優化設計思路及方法有效可靠。

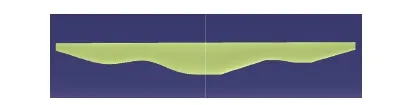
圖10 優化機翼后緣修正示意圖Fig.10 P-optimal wing TE-corrected view

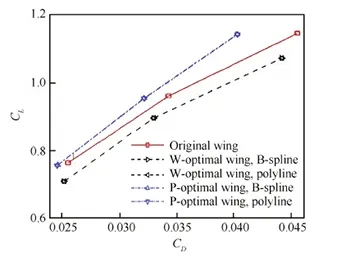
圖11 優化前后機翼CFD方法計算結果對比Fig.11 Comparison of CFD numerical results before and after wing optimization

4 結 論

1) 以CFD準定常求解方法為參考，本文發展的渦格法準定常求解程序及低雷諾數修正方法針對低雷諾數條件下的多螺旋槳/機翼相互氣動干擾問題具備較高的數值計算精度以及突出的數值計算效率，且其計算結果能夠在一定程度上準確反映螺旋槳滑流影響下機翼表面力分布特征。

2) 在本文研究的低雷諾數狀態下，螺旋槳滑流對機翼氣動特性的影響表現為增升增阻，同時由機翼展向力分布還可以看出螺旋槳對氣流的加速效應極為顯著，而旋轉效應則相對較弱。

3) 本文基于VLM-LRC方法提出的通過控制機翼表面形狀來獲得最優橢圓形升力分布的設計思路有效可靠，在螺旋槳停機及工作狀態下分別進行優化設計的機翼相對同等狀態原始機翼誘導阻力可降低達20.8 counts和13.4 counts。而最終采用CFD方法進行驗證的優化機翼“P-optimal wing”總阻力可相對降低達19.52 counts，減阻效果顯著。

4) 對于多螺旋槳驅動的太陽能無人機而言，螺旋槳滑流影響將為全機帶來較為顯著的附加氣動力，這可能會導致傳統僅僅針對主要升力面進行優化設計的無人機飛行性能偏離設計點，甚至產生負面作用。因此，耦合動力系統氣動影響的無人機優化設計思路更具實際工程意義。

參 考 文 獻

[1] ROMEO G, FRULLA G, CESTINO E, et al. Heliplat: Design, aerodynamic, structural analysis of long-endurance solar-powered stratospheric platform[J]. Journal of Aircraft, 2004, 41(6): 1505-1520.

[2] EHAB A E, COLIN P B. Experimental investigation of the effect of propeller slipstream on boundary layer behavior at low Reynolds number[J]. AIAA-Applied Aerodynamics Conference, 2000, 194(10): 267-276.

[3] 王科雷, 周洲, 甘文彪, 等. 太陽能無人機低雷諾數翼型氣動特性研究[J]. 西北工業大學學報, 2014, 32(2): 163-168.

WANG K L, ZHOU Z, GAN W B, et al. Studying aerodynamic performance of the low-Reynolds-number airfoil of solar energy UAV[J]. Journal of Northwestern Polytechnical University, 2014, 32(2): 163-168 (in Chinese).

[4] GAVIN K A, ROBERT W D, MICHAEL S S. Propeller induced flow effects on wings at low Reynolds numbers: AIAA-2013-3193[R]. Reston： AIAA, 2013.

[5] KROO I. Propeller-wing integration for minimum induced loss[J]. Journal of Aircraft, 1986, 23(7): 561-565.

[6] VELDHUIS L L M, HEYMA P M. A simple wing optimization code including propeller effects[C]//21st Congress of the International Council of the Aeronautical Sciences. [S.l.]： ICAS, 1998.

[7] VELDHUIS L L M, HEYMA P M. Aerodynamic optimization of wings in multi-engined tractor propeller arrangements[J]. Aircraft Design, 2000, 3(3): 129-149.

[8] VELDHUIS L L M. Propeller/wing aerodynamic interference[D]. Delft: Delft University of Technology, 2005.

[9] RAKSHITH B R, DESHPANDE S M, RODDAM N, et al. Optimal low-drag wing planforms for tractor-configuration propeller-driven aircraft[J]. Journal of Aircraft, 2015, 52(6): 1-11.

[10] 喬宇航, 馬東立, 鄧小剛. 基于升力線理論的機翼幾何扭轉設計方法[J]. 北京航空航天大學學報, 2013, 39(3): 320-324.

QIAO Y H, MA D L, DENG X G. Wing geometric twist design method based on lifting-line theory[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(3): 320-324 (in Chinese).

[11] 徐家寬, 白俊強, 黃江濤, 等. 考慮螺旋槳滑流影響的機翼氣動優化設計研究[J]. 航空學報, 2014, 35(11): 2910-2920.

XU J K, BAI J Q, HUANG J T, et al. Aerodynamic optimization design of wing under the interaction of propeller slipstream[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(11): 2910-2920 (in Chinese).

[12] 陳廣強, 白鵬, 詹慧玲, 等. 高空長航時無人機螺旋槳滑流效應影響研究[J]. 飛機設計, 2014, 34(4): 1-9.

CHEN G Q, BAI P, ZHAN H L, et al. Numerical simulation study on propeller slipstream effect on high altitude long endurance unmanned air vehicle (HALE UAV)[J]. Aircraft Design, 2014, 34(4): 1-9 (in Chinese).

[13] 陳廣強, 白鵬, 詹慧玲, 等. 一種推進式螺旋槳無人機滑流效應影響研究[J]. 空氣動力學學報, 2015, 33(4): 554-562.

CHEN G Q, BAI P, ZHAN H L, et al. Numerical simulation study on propeller slipstream effect on unmanned air vehicle with propeller engine[J]. Acta Aerodynamica Sinica, 2015, 33(4): 554-562 (in Chinese).

[14] 孫美建, 詹浩. Kriging模型在機翼氣動外形優化中的應用[J]. 空氣動力學報, 2011, 29(6): 759-764.

SUN M J, ZHAN H. Application of Kriging surrogate model for aerodynamic shape optimization of wing[J]. Acta Aerodynamica Sinca, 2011, 29(6): 759-764 (in Chinese).

[15] 穆雪峰, 姚衛星, 余雄慶, 等. 多學科設計優化中常用代理模型的研究[J]. 計算力學學報, 2005, 22(5): 608-612.

MU X F, YAO W X, YU X Q, et al. A survey of surrogate models used in MDO[J]. Chinese Journal of Computational Mechanics, 2005, 22(5): 608-612 (in Chinese).

[16] ESMAEEL E, MEHRAN T, SAMAN N. Aerodynamic performance of Parastoo UAV[J]. Aircraft Engineering and Aerospace Technology: An International Journal, 2013, 85(2): 97-103.

[17] 甘文彪, 周洲, 許曉平. 仿生全翼式太陽能無人機氣動數值模擬[J]. 航空學報, 2015, 36(10): 3284-3294.

GAN W B, ZHOU Z, XU X P. Aerodynamic numerical simulation of bionic full-wing typical solar-powered unmanned aerial vehicle[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(10): 3284-3294 (in Chinese).

[18] 甘文彪, 周洲, 許曉平. 仿生全翼式太陽能無人機分層協同設計及分析[J]. 航空學報, 2016, 37(1): 163-178.

GAN W B, ZHOU Z, XU X P. Multilevel collaboration design and analysis of bionic full-wing typical solar-powered unmanned aerial vehicle[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(1): 163-178 (in Chinese).

[19] MICHAEL D P, BRIAN J G. Wing aerodynamic analysis incorporating one-way interaction with distributed propellers： AIAA-2014-2852[R]. Reston： AIAA, 2014.

[20] RANGWALLA A A, WILSON L N. Application of a panel code to unsteady wing-propeller interference[J]. Journal of Aircraft, 1987, 24(8): 568-571.

[21] 遲永一. 基于CFD方法的輕型公務機雷諾數修正研究[J]. 黑龍江科技信息, 2014(17): 122.

CHI Y Y. A study of CFD-based Reynolds correction for light business jets[J]. Heilongjiang Science and Technology Information, 2014(17): 122 (in Chinese).

[22] 張輝, 李杰, 龔志斌. 某運輸機全機構型雷諾數效應阻力修正研究[J]. 飛行力學, 2012, 30(1): 20-24.

ZHANG H, LI J, GONG Z B. Drag correction to higher Reynolds number for a transport aircraft[J]. Flight Dynamics, 2012, 30(1): 20-24 (in Chinese).

[23] 王巍, 李東升, 劉春. 基于小擾動理論的槳葉葉素氣動載荷計算方法[J]. 北京航空航天大學學報, 2016, 42(2): 294-302.

WANG W, LI D S, LIU C. Calculation method of blade element aerodynamic loads based on small perturbation theory[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(2): 294-302 (in Chinese).

[24] WALTERS D K, COKLJAT D. A three-equation eddy-viscosity model for Reynolds-averaged Navier-Stokes simulations of transitional flows[J]. Journal of Fluids Engineering, 2008, 130(1): 1-14.

[25] WALTERS D K, LEYLEK J H. Impact of film-cooling jets on turbine aerodynamic losses[J]. Journal of Turbomachinery, 2000, 122(3): 537-545.

[26] VOLINO R J. A new model for free-stream turbulence effects on boundary layers[J]. Journal of Turbomachinery, 1998(120): 613-620.

[27] HSIAO F B, LIU C F, TANG Z. Experimental studies of airfoil performance and flow structures on a low Reynolds number airfoil[C]//19th AIAA, Fluid Dynamics, Plasma Dynamics, and Lasers Conference, Honolulu, 1987.

[28] ABTAHI A A, MARCHMAN J F. Aerodynamics of an aspect ratio 8 wing at low Reynolds number[J]. AIAA Journal, 1985, 22(7): 628-634.

[29] 張家樹, 楊恬. 三次B樣條曲線的快速生成算法[J]. 西南師范大學學報(自然科學版), 1997, 22(6): 644-647.

ZHANG J S, YANG T. A fast generating algorithm of gubic B-spline curve[J]. Journal of Southwest China Normal University (Natural Science), 1997, 22(6): 644-647 (in Chinese).

[30] 榮煥宗, 張偉榮, 張蔚. 帶有面積約束的B樣條曲線擬合方法[J]. 應用數學與計算數學學報, 1990, 4(2): 19-25.

RONG H Z, ZHANG W R, ZHANG W. B-spline curve fitting method with an area constraint[J]. Communication on Applied Mathematics and Computation, 1990, 4(2): 19-25 (in Chinese).

[31] 王小平, 曹立明. 遺傳算法-理論、應用與軟件實現[M]. 西安： 西安交通大學出版社, 2002.

WANG X P, CAO L M. Genetic algorithm-theory, application and realization[M]. Xi’an: Xi’an Jiaotong University Press, 2002 (in Chinese).

[32] 譚艷艷. 幾種改進的分解類多目標進化算法及其應用[D]. 西安： 西安電子科技大學, 2013.

TAN Y Y. Several modified decomposition-based multi-objective evolutionary algorithms and their applications[D]. Xi’an: Xidian Univeristy, 2013 (in Chinese).

(責任編輯： 鮑亞平)

Aerodynamic design of low-Reynolds-number wing taking intoaccount the multiple propellers induced effects

WANGKelei1,2,ZHOUZhou1,2,*,ZHUXiaoping2

1.CollegeofAeronautics,NorthwesternPolytechnicalUniversity,Xi’an710072,China2.LaboratoryofScienceandTechnologyonUAV,NorthwesternPolytechnicalUniversity,Xi’an710065,China

Based on a certain hand-throw solar-powered unmanned aerial vehicle (UAV), the optimization design approaches for low-Reynolds-number wing coupled with multiple propellers induced effects are studied. The corresponding quasi-steady procedure based on the vortex lattice method (VLM) of lifting line theory and the low Reynolds correction (LRC) method based on the reference airfoil aerodynamic properties database are developed to simulate the multiple propellers/wing aerodynamic interference at low Reynolds numbers. The reliability and accuracy of the simplified numerical method (VLM procedure and LRC method) are testified with several cases studies and their comparison with experimental results. Both the direct optimization design and inverse design of the simplified hand-throw solar-powered UAV model in tractor configuration are conducted, and the optimization results are examined with high-accuracy CFD technique. It shows that (a) the low-Reynolds-number flow can be simulated by the VLM-LRC method efficiently and accurately; (b) the aerodynamic properties of the optimal wing cannot be improved when the propeller slipstream effect is not taken into consideration in the conventional design approach; (c) the wing drag performance can be greatly improved with the optimization approach that takes into account the multiple propeller slipstream effects, and the optimized wing has a drag reduction of 19.52 counts at the design state.

hand-throw solar-powered unmanned aerial vehicle; low-Reynolds-number wing; multiple propellers/wing aerodynamic interference; vortex lattice method; low Reynolds correction; optimal design; inverse design

2016-09-23；Revised2016-12-03；Accepted2016-12-19；Publishedonline2017-01-041433

URL：www.cnki.net/kcms/detail/11.1929.V.20170104.1433.004.html

s：CivilAircraftProject(MIZ-2015-F-009);ShaanxiProvinceScienceandTechnologyProject(2015KTCQ01-78)

2016-09-23；退修日期2016-12-03；錄用日期2016-12-19； < class="emphasis_bold">網絡出版時間

時間：2017-01-041433

www.cnki.net/kcms/detail/11.1929.V.20170104.1433.004.html

民機專項 (MIZ-2015-F-009)； 陜西省科技統籌 (2015KTCQ01-78)

*

.E-mailzhouzhou@nwpu.edu.cn

王科雷， 周洲， 祝小平． 耦合多螺旋槳滑流影響的低雷諾數機翼設計J． 航空學報,2017,38(6):120813.WANGKL,ZHOUZ,ZHUXP.Aerodynamicdesignoflow-Reynolds-numberwingtakingintoaccountthemultiplepropellersinducedeffectsJ.ActaAeronauticaetAstronauticaSinica,2017,38(6):120813.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.120813

V211

A

1000-6893(2017)06-120813-13

*Correspondingauthor.E-mailzhouzhou@nwpu.edu.cn