航天器姿控系統的PD型學習觀測器故障重構

張科， 韓治國， 郭小紅， 呂梅柏

1.西北工業大學 航天學院， 西安 710072 2.西北工業大學 航天飛行動力學技術重點實驗室， 西安 710072 3.西安衛星測控中心， 西安 710043

航天器姿控系統的PD型學習觀測器故障重構

張科1,2,*， 韓治國1,2， 郭小紅3， 呂梅柏1,2

1.西北工業大學 航天學院， 西安 710072 2.西北工業大學 航天飛行動力學技術重點實驗室， 西安 710072 3.西安衛星測控中心， 西安 710043

針對滿足Lipschitz條件的航天器姿態控制系統這一非線性系統中存在的執行器加性故障、空間干擾與測量噪聲問題，提出了基于PD型迭代學習觀測器的故障重構方法。該方法具有期望的魯棒性能指標，能夠在系統存在空間干擾與測量噪聲情況下實現對突變故障與時變故障等故障類型的精確重構。基于線性矩陣不等式技術給出系統化PD型迭代學習觀測器的設計方法，并根據Lyapunov穩定性理論對上述設計方法的穩定性條件進行了理論證明，同時利用魯棒技術抑制空間干擾與測量噪聲對執行器故障重構的影響，通過線性矩陣不等式工具箱求解觀測器參數矩陣。最后，將該方法應用到航天器姿態控制系統中，仿真結果證明了該方法的有效性。

故障重構； 迭代學習； 非線性系統； 姿控系統； 航天器

隨著高性能與高可靠性要求的增加，航天器姿態控制系統(Spacecraft Attitude Control System, SACS)變得越來越精細與復雜。由于航天器長期運行在惡劣的空間環境，這樣的復雜系統不可避免地存在各種各樣的故障，這些故障將會降低系統的性能，甚至帶來災難性的后果。因此，研究航天器姿態控制系統故障重構問題有利于提高系統的可靠性，保障飛行任務的順利完成。近幾年來航天器姿態控制系統故障重構問題越來越受到研究者的重視，成為重要的研究方向[1-4]。

自20世紀90年代以來，學習觀測器越來越受到研究者的重視[5]。與其他觀測器相比，學習觀測器具有設計復雜度小、運算量少、魯棒性強、故障約束寬松等優點，在進行故障重構時，故障重構信號只需根據歷史故障信息和當前測量輸出估計誤差遞推更新生成，無需進行積分運算。因此，基于迭代學習觀測器的故障重構技術成為故障重構的重要研究方向，并且取得了一系列富有成效的研究成果[6-11]。文獻[6]首次提出迭代學習觀測器的概念，同時根據此觀測器對非線性系統進行故障檢測與調節。文獻[7]使用迭代學習觀測器對系統時變參數進行辨識，同時能夠估計系統狀態。文獻[8]根據迭代學習觀測器對航天器姿態控制系統進行故障檢測、隔離與估計。文獻[9]將迭代學習與未知輸入觀測器相結合的魯棒容錯控制方法應用于航天器在軌運行時存在的執行機構故障和空間干擾問題。該方法利用未知輸入觀測器實現了空間干擾的解耦問題，同時利用上一時刻的偏差信息實現執行機構在線故障重構。文獻[10]針對存在執行器故障、傳感器故障與推力器故障的線性系統，提出了基于PD型學習觀測器的重構故障方法，同時根據魯棒性能指標設計了PD型學習觀測器抑制干擾輸入對故障重構的影響。但是該方法只是針對線性系統，并且沒有考慮系統測量噪聲對故障重構的影響。文獻[11]針對航天器姿態控制系統出現的執行器故障，提出了一種基于迭代學習-未知輸入觀測器的魯棒故障重構方法，采用未知輸入觀測器實現干擾解耦，利用迭代學習算法實現故障重構。但是該方法在求解觀測器參數時較為繁瑣，約束較多，也沒有考慮系統的測量噪聲對故障重構的影響。

基于上述研究，在綜合考慮空間干擾與測量噪聲下，針對滿足Lipschitz條件的航天器姿態控制系統，本文提出了一種魯棒PD型迭代學習觀測器的故障重構方法。通過引入魯棒性能指標，使得設計的迭代學習觀測器對空間干擾與測量噪聲具有魯棒性，利用線性矩陣不等式技術給出系統化的增益矩陣求解方法。最后，將所提故障重構方法應用于航天器姿態控制系統執行器故障重構問題，仿真結果說明了該方法的有效性。

1 問題描述

根據文獻[9-12]，航天器姿態動力學方程可以描述為

(1)

式中：J=diag(J1,J2,J3)為航天器的轉動慣量;ω=[ωxωyωz]T為航天器本體相對慣性坐標系的角速度在星體坐標系中的表示;Tc=[Tc1Tc2Tc3]T為控制力矩;ω0為軌道角速度;ζ=[-sinθsinφcosθcosφcosθ]T為非線性項，歐拉角φ,θ,ψ分別為滾轉、俯仰與偏航角；Td=[Td1Td2Td3]T為外部干擾力矩；ω×定義為

(2)

選取主慣量軸為本體坐標系，忽略剛體航天器慣量積，則航天器姿態動力學方程簡化為[11]

(3)

考慮剛體航天器運行于小角度工況下，則航天器姿態運動學方程簡化為

(4)

結合式(3)與式(4)，建立航天器姿態動力學方程為[13]

(5)

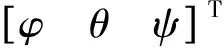
V=

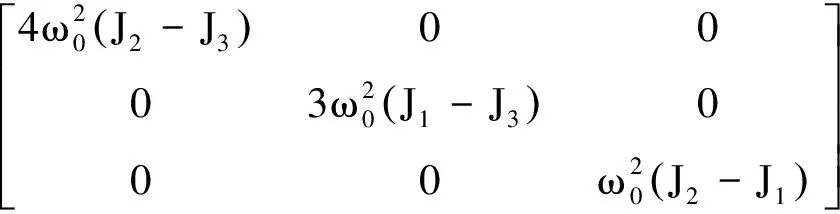
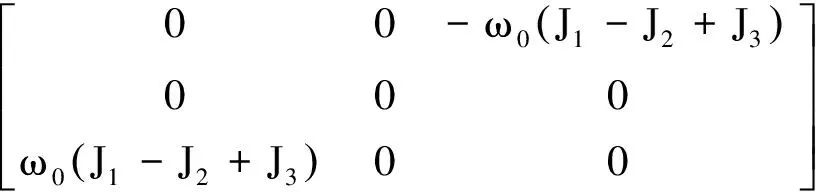
(6)

(7)

注釋1本文選擇微小航天器作為研究對象。微小航天器的姿態控制系統不同于較大航天器，較大航天器的柔性與模型的緩變衰減是建模時應該考慮的影響因素。而對于微小航天器，由于不存在柔性特性，可以把它作為剛體進行考慮。

為了獲得主要結論，給出如下假設與引理。

假設1假設式(7)中系統能控能觀，非線性項f(x,t)滿足Lipschitz條件[13-14]，即

(8)

式中：γ>0為Lipschitz常數。

引理1給定適維矩陣X和Z，存在對稱正定矩陣H1使得如下不等式成立[16]：

XTZ+ZTX≤XTH1X+ZTH1-1Z

(9)

引理2對于給定矩陣A1∈Rn×n，當且僅當存在對稱正定矩陣P1∈Rn×n使得如下不等式成立[16]：

(10)

式中：*表示對稱矩陣項，則矩陣A1的全部特征值位于圓形穩定域D(α,r)，其中α和r分別為圓心和半徑。

2 基于PD型學習觀測器的執行器加性故障重構

2.1 PD型學習觀測器設計

針對式(7)中系統模型，設計如下的PD型學習觀測器(Learning Observer, LO)[10,17-18]

(11)

定義狀態估計誤差ex(t)、輸出估計誤差ey(t)和故障重構誤差ef(t)如下：

(12)

結合式(7)與式(11)，可得誤差方程如下：

(13)

為了利用PD型學習觀測器式(11)重構執行器加性故障，給出如下假設：

注釋2從假設3可以看出，該假設具有明確的物理意義，即要求執行器故障增量范數有界。

2.2 PD型學習觀測器穩定性分析

為了使得PD型學習觀測器式(11)能夠精確重構執行器加性故障，給出如下定理：

定理1若假設1～假設3成立且存在對稱正定矩陣P∈Rn×n，Q∈Rn×n以及矩陣K∈Rm×p和Y∈Rn×p使得如下條件成立：

(14)

(15)

(16)

KCFa-Im=0

(17)

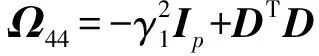
(18)

式中：wd(t)=[dT(t)dT(t-τ)ηT(t)NT(t)]T；kq為中間變量。

證明選取Lyapunov函數[10,17]

(19)

對Lyapunov函數求導，得

(20)

根據引理1與假設1～假設2，有如下不等式成立：

(21)

(22)

(23)

(24)

(25)

式中：λmax為矩陣L的最大特征值。如果條件式(16)與式(17)成立，把式(21)～式(25)代入式(20)得

2σPFaKC+2PFaKC+PP+γ2In+

(26)

如果條件式(15)成立，根據Schur補引理可得

(27)

另外，如果條件σ≥1滿足，則-2σPFaKC+2PFaKC≤0，因此有下式成立：

(28)

式中：

定義H∞性能指標為[17]

(29)

在零初始條件下，可得

(30)

式中：

(31)

因此，如果假設2與假設3成立，則H∞性能指標式(18)成立。如果Μ2<0成立，令Y=PL，根據Schur補引理可得不等式(14)成立。證畢。

注釋3為了矩陣求解方便，將式(16)轉化為如下不等式進行求解[10]：

(32)

式中：μ>0。μ越小，上述不等式越接近式(16)。在求解μ時，可以設置μ為充分小的常量，或者通過MATLAB/LMI工具箱求解器mincx進行求解。

注釋4為了保證PD型學習觀測器的收斂速度，將矩陣A-LC的特征配置在區域D(α,r)，根據引理2可得如下的線性矩陣不等式：

(33)

式中：α<0,r>0，且|α|≥r。

注釋5對于定理1，應用最小二乘法求解等式(17)可得矩陣K，通過求解不等式(14)、式(15)、式(32)與式(33)可以獲得觀測器矩陣L。

注釋6對于定理1，為了保證所設計的觀測器具有可行解，根據文獻[10,19-21]，所設計的觀測器存在可行解的充分條件為

(34)

根據文獻[20-21]，上述充分條件等價于：(A,Fa,C)的不變零點位于復平面的左半平面。

注釋7執行器故障可以采用加性或者乘性形式進行標示，且這2種故障形式可以相互轉換。突變型故障為加性形式故障標示方式，在工程實際中，對應卡死、偏置等故障現象。時變型故障為乘性形式故障標示方式，在工程實際中，對應執行器效率下降等故障現象。

3 仿真校驗

為驗證本文方法的有效性，將上述方法應用于航天器姿態控制系統執行器加性故障重構問題。選擇的典型航天器參數如表1所示[22]，其中?為姿態角。

干擾力矩為[23]

式中：A0=1.5×10-5N·m。

在進行不等式求解時，選擇參數γ=0.01，γ1=2，σ=1，τ=0.01 s，μ=10-6，r=10，α=-10。

表1 航天器參數Table 1 Spacecraft parameters

根據上述仿真參數，利用條件式(17)可得

利用MATLAB/LMI工具箱求解條件式(14)、式(15)、式(32)與式(33)，可得

3.1 突變型執行機構加性故障重構

假設執行器出現突變型故障，故障形式為

(35)

(36)

(37)

采用定理1設計的PD型迭代學習觀測器實現對執行器故障式(35)～式(37)重構，重構結果如圖1所示。

從圖1中可以看出，當執行器發生突變故障時，基于迭代學習觀測器的故障重構方法能夠在很短的時間內實現對突變故障的精確重構，且該觀測器能夠同時實現對多方向突變故障的精確重構。從局部放大圖可以看出，故障重構精度很高，誤差很小。

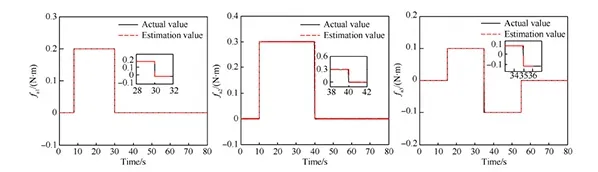
圖1 突變故障重構曲線Fig.1 Curves of abrupt fault reconstruction

3.2 時變型執行機構加性故障重構

假設執行器出現時變型故障，故障形式為

(38)

(39)

(40)

根據上述仿真參數，采用定理1設計的PD型學習觀測器實現對執行器故障式(38)～式(40)重構，重構結果如圖2所示。從圖中可知，當執行器發生時變故障時，本文提出的故障重構方法能夠在很短的時間內實現對時變型加性故障的精確重構，故障重構精度高，在突變點處也能完全重構實際故障。另外，對于正弦形式變化的時變故障，本文提出的故障重構方法也能實現精確重構(如圖2(a))。因此，對于緩變故障與正弦形式變化的故障，本文給出的故障重構方法均能實現很好的故障重構。

圖3為對時變型故障的故障重構誤差。從圖中可以看出，故障重構誤差非常小，對于正弦形式變化的故障，重構誤差量級為10-3，對于緩變形式變化的故障，重構誤差量級為10-4。因此，上述仿真結果說明了本文方法對航天器姿態控制系統執行器加性故障重構的有效性。

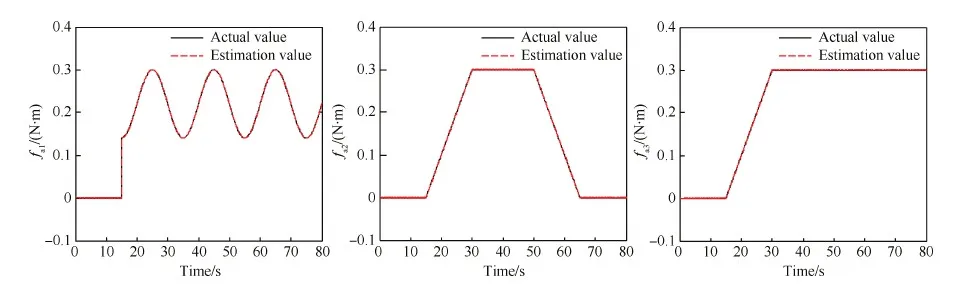
圖2 時變故障重構曲線Fig.2 Curves of time-varying fault reconstruction

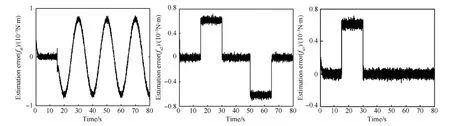
圖3 時變故障重構曲線誤差Fig.3 Errors of curves of time-varying fault reconstruction

4 結 論

本文針對滿足Lipschitz條件的航天器姿態控制系統中存在的執行器加性故障、空間干擾與測量噪聲問題，提出了一種基于PD型迭代學習觀測器的故障重構方法。該方法具有如下優勢：

1) 能夠在系統存在空間干擾與測量噪聲情況下實現對突變故障與時變故障等故障類型的精確重構。

2) 通過引入H∞性能指標能夠抑制空間干擾與測量噪聲對故障重構的影響。

[1] NGUANG S K, SHI P, DING S. Fault detection filter for uncertain fuzzy systems: An LMI approach[J]. IFAC Proceedings volumes, 2005, 38(1): 227-232.

[2] ZHANG Z, JAIMOUKHA I M. On-line fault detection and isolation for linear discrete-time uncertain systems[J]. Automatica, 2014, 50(2): 513-518.

[3] FENG J, WANG S, ZHAO Q. Closed-loop design of fault detection for networked non-linear systems with mixed delays and packet losses[J]. IET Control Theory and Applications, 2013, 7(6): 858-868.

[4] ZHANG J, SWAIN A K, NGUANG S K. RobustH∞adaptive descriptor observer design for fault estimation of uncertain nonlinear systems[J]. Journal of the Franklin Institute, 2014, 351(11): 5162-5181.

[5] 陶洪峰, 鄒偉, 楊慧中. 執行器故障多率采樣間歇過程的魯棒耗散迭代學習容錯控制[J]. 控制理論與應用, 2012, 33(3): 329-335.

TAO H F, ZOU W, YANG H Z. Robust dissipative iterative learning fault-tolerant control for multi-rate sampling batch process with actuator failure[J]. Control Theory and Applications, 2012, 33(3): 329-335 (in Chinese).

[6] CHEN W, SAIF M. An iterative learning observer-based approach to fault detection and accommodation in nonlinear systems[C]//Proceedings of the 40th IEEE Conference on Decision and Control. Piscataway, NJ: IEEE Press, 2001: 24-26.

[7] CHEN W, ER M J. Simulations identification of time-varying parameters and estimation of system states using iterative learning observers[J]. International Journal of Systems Science, 2007, 38(1): 39-45.

[8] WU Q, SAIF M. Repetitive learning observer based actuator fault detection, isolation, and estimation with application to a satellite attitude control system[C]//Proceedings of the 2007 American Control Conference. Piscataway, NJ: IEEE Press, 2007: 414-419.

[9] 管宇, 張迎春, 沈毅, 等. 基于迭代學習觀測器的衛星姿態控制系統的魯棒容錯控制[J]. 宇航學報, 2012, 33(8): 1080-1086.

GUAN Y, ZHANG Y C, SHEN Y, et al. Fault-tolerant control for satellite attitude control system based on iterative learning observer[J]. Journal of Astronautics, 2012, 33(8): 1080-1086 (in Chinese).

[10] 賈慶賢. 基于學習觀測器的衛星姿態控制系統故障重構研究[D]. 哈爾濱: 哈爾濱工業大學, 2015: 55-65.

JIA Q X. Research on learning observer-based fault reconstruction for satellite attitude control system[D]. Harbin: Harbin Institute of Technology, 2015: 55-65 (in Chinese).

[11] 賈慶賢, 張迎春, 沈毅, 等. 基于迭代學習-未知輸入觀測器的衛星姿控系統魯棒故障重構[J]. 系統工程與電子技術, 2012, 34(1): 120-124.

JIA Q X, ZHANG Y C, SHEN Y, et al. Robust fault reconstruction method for satellite attitude control system based on iterative learning-unknown input observer[J]. Systems Engineering and Electronics, 2012, 34(1): 120-124 (in Chinese).

[12] JIA Q X, CHEN W, ZHANG Y C, et al. Fault reconstruction and fault-tolerant control via learning observer in Takagi-Sugeno fuzzy descriptor systems with time delays[J]. IEEE Transactions on Industrial Electronics, 2015, 62(6): 3885-3895.

[13] GAO Z F, JIANG B, SHI P, et al. Sensor fault estimation and compensation for microsatellite attitude control system[J]. International Journal of Control, Automation, and Systems, 2010, 8(2): 228-237.

[14] ZHANG J, SWAIN A K, NGUANG S K. Robust sensor fault estimation scheme for satellite attitude control systems[J]. Journal of the Franklin Institute, 2013, 350(9): 2581-2604.

[15] SOBHANI-TEHRANI E, KHORASANI K. Fault diagnosis of nonlinear systems using a hybrid approach[M]. Berlin: Springer, 2009: 19-117.

[16] 俞立. 魯棒控制——線性矩陣不等式處理方法[M]. 北京: 清華大學出版社, 2002: 6-29.

YU L. Robust control-linear matrix inequality method[M]. Beijing: Tsinghua University Press, 2002: 6-29 (in Chinese).

[17] LIU C, YANG H, CHEN W, et al. A novel design of iterative learning observer for fault estimation[C]//2011 ASME/IEEE International Conferences on Mechatronic and Embedded Systems and Applications. Washington, D.C.: ASME, 2011: 435-439.

[18] JIA Q X, CHEN W, ZHANG Y C, et al. Robust fault reconstruction via learning observers in linear parameter-varying systems subject to loss of actuator effectiveness[J]. IET Control Theory and Applications, 2014, 8(1): 42-50.

[19] XU J X, PANDA S K, LEE T H. Real-time iterative learning control[M]. Berlin: Springer, 2009: 7-26.

[20] TAN C P. Sliding mode observer for fault detection and isolation[D]. Leicester: University of Leicester, 2002: 35-142.

[21] EDWARDS C, YAN X G, SPURGEON S K. On the solvability of the constrained Lyapunov problem[J]. IEEE Transactions on Automatic Control, 2007, 52(10): 1982-1987.

[22] 賈慶賢, 張迎春, 陳雪芹, 等. 衛星姿態控制系統故障重構觀測器設計[J]. 宇航學報, 2016, 37(4): 442-450.

JIA Q X, ZHANG Y C, CHEN X Q, et al. Observer design for fault reconstruction in satellite attitude control system[J]. Journal of Astronautics, 2016, 37(4): 442-450 (in Chinese).

[23] 張迎春, 賈慶賢, 李化義, 等. 基于比例積分觀測器的衛星姿控系統魯棒故障重構[J]. 系統工程與電子技術, 2014, 36(9): 1810-1818.

ZHANG Y C, JIA Q X, LI H Y, et al. Robust fault reconstruction design for satellite attitude control systems based on proportional integral observer[J]. Systems Engineering and Electronics, 2014, 36(9): 1810-1818 (in Chinese).

(責任編輯： 張玉， 王嬌)

PD-type learning observer based fault reconstruction forspacecraft attitude control systems

ZHANGKe1,2,*,HANZhiguo1,2,GUOXiaohong3,LYUMeibo1,2

1.SchoolofAstronautics,NorthwesternPolytechnicalUniversity,Xi’an710072,China2.NationalKeyLaboratoryofAerospaceFlightDynamics,NorthwesternPolytechnicalUniversity,Xi’an710072,China3.ChinaXi’anSatelliteControlCenter,Xi’an710043,China

A fault reconstruction method based on PD-type iterative learning observer is proposed to deal with actuator additive faults, space external disturbances and measurement noises existing in the nonlinear systems such as spacecraft attitude control systems, which satisfy Lipschitz conditions. The method has the desired robust performance index, and can achieve accurate reconstruction of abrupt faults, time-varying faults, etc. in the presence of space external disturbances and measurement noises. The designed method of PD-type iterative learning observer is given based on linear matrix inequality technique, and the stability condition of the method is proved according to the Lyapunov stability theory. The influence of space external disturbances and measurement noises on actuator additive faults reconstruction is suppressed using robust technology and also linear matrix inequality toolkit solving observer parameter matrix. The method is applied to spacecraft attitude control system. Simulation results show the effectiveness of the proposed method.

fault reconstruction; iterative learning; nonlinear system; attitude control system; spacecraft

2016-07-20；Revised2016-08-29；Accepted2016-09-21；Publishedonline2016-10-081518

URL：www.cnki.net/kcms/detail/11.1929.V.20161008.1518.002.html

s：NationalNaturalScienceFoundationofChina(61502391);ChinaSpaceFoundation(N2015KC0121)

2016-07-20；退修日期2016-08-29；錄用日期2016-09-21； < class="emphasis_bold">網絡出版時間

時間：2016-10-081518

www.cnki.net/kcms/detail/11.1929.V.20161008.1518.002.html

國家自然科學基金 (61502391)； 航天支撐基金 (N2015KC0121)

*

.E-mailzhangke@nwpu.edu.cn

張科， 韓治國， 郭小紅， 等． 航天器姿控系統的PD型學習觀測器故障重構J． 航空學報,2017,38(6):320629.ZHANGK,HANZG,GUOXH,etal.PD-typelearningobserverbasedfaultreconstructionforspacecraftattitudecontrolsystemsJ.ActaAeronauticaetAstronauticaSinica,2017,38(6):320629.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0259

V448.2

A

1000-6893(2017)06-320629-09

*Correspondingauthor.E-mailzhangke@nwpu.edu.cn