適用于參數可調結構的非定常氣動力降階建模方法

王梓伊， 張偉偉

西北工業大學 航空學院， 西安 710072

適用于參數可調結構的非定常氣動力降階建模方法

王梓伊， 張偉偉*

西北工業大學 航空學院， 西安 710072

基于計算流體力學(CFD)的非定常氣動力降階模型(ROM)可以極大提高氣動彈性分析效率，然而現有的ROM只能針對固定參數結構，即只適合于固定模態振型，這使得現有ROM在氣動彈性優化設計和不確定性分析等結構變參問題中應用受限。針對該問題，在文獻[20]基礎上提出了一種新的適用于任意模態振型的非定常氣動力建模方法。首先將待設計/分析的結構進行參數化抽樣和模態分析，之后通過主成分分析(PCA)得到若干基振型，再將這些基振型線性疊加即可擬合抽樣空間內任何參數下結構的前若干階振型。當結構參數改動時，僅僅是疊加系數發生變化。算例表明，僅用很少的基振型就能達到理想的擬合精度。經典的氣動力降階方法可用于基振型坐標下的氣動力降階，進一步變換可得到適用于不同結構的ROM，這意味著，結構參數可以在抽樣空間內任意調節改動，而ROM卻是通用的。該方法能廣泛用于氣動彈性優化設計和不確定性分析工作，可提高顫振分析精度和效率。

結構優化； 參數變動； 降階模型(ROM)； 跨聲速流； 顫振； 非定常氣動力

為了提高氣動彈性分析的效率，工程上常借助線化勢流理論來計算氣動力，然而，該方法并不適用于跨聲速和大迎角的情況。由于大型客機和大型運輸機等飛行器的巡航速度處于跨聲速區，并且很多殲擊機也需要在跨聲速區保持必要的作戰性能，在這種情況下，基于線化理論的非定常氣動力建模方法便不再適用。隨著CFD技術的發展，直接基于CFD的求解方法為跨聲速區氣動彈性問題提供了新的解決思路，但由于該方法需要消耗大量的計算資源和時間成本，因此目前主要用作后期驗證。

為了降低CFD方法分析氣動彈性問題的計算成本，很多學者進行了氣動力降階方法相關研究。Dowell[1]、Lucia[2]、張偉偉[3]和陳剛[4]等對非定常氣動力降階建模方法及其在氣動彈性分析中的應用做了詳細論述。可以看到，在非定常氣動力降階中，主要應用了兩種方法：本征正交分解(Proper Orthogonal Decomposition, POD)法和系統辨識方法。系統辨識方法包括積分方法和差分方法，比如Volterra級數方法屬于積分方法，而ARX(Auto Regressive with eXogenous input)模型則屬于差分方法。在文獻[5-7]中，基于ARX模型的非定常氣動力降階建模方法已經應用于帶操縱面機翼的跨聲速顫振分析[5]、大迎角顫振分析[6]、跨聲速顫振主動抑制控制率設計[7]等實際問題。在文獻[8-10]中，非定常氣動力降階建模方法已經應用于跨聲速極限環振蕩分析。在這些分析中，非定常氣動力降階模型(ROM)(如POD[8]、Volterra級數[9]、ARX模型[10])是靜態非線性、動態線性的，極限環振蕩的非線性來源于結構的非線性。對于跨聲速流動中小振幅的顫振分析，這些非定常氣動力降階模型是適用的。在文獻[11-15]中，徑向基函數神經網絡模型已經用于構建跨聲速流動中動態非線性的非定常氣動力降階模型。這些非定常氣動力降階模型成功預測了結構線性、氣動力動態非線性的極限環振蕩。

盡管取得很大進展，但上述ROM方法只能針對給定結構。當結構發生改動時，模態頻率和模態振型一般都會隨之變化。目前，模態坐標下的氣動力模型能夠適應模態質量或模態頻率的變化[16-17]，卻不能適應模態振型的變化。文獻[18-19]表明，如果僅考慮模態頻率而忽視模態振型的變化，顫振預測的結果將不可信。換言之，一旦結構改動并引發振型變化，就必須重新建立適用于新振型的ROM，這就需要再次啟動CFD求解器以采集訓練數據。在氣動彈性優化設計中，如果將顫振速度作為優化問題的一個約束條件來優化結構參數(如梁的位置、蒙皮厚度等)，那么，優化過程中需要不斷地計算不同結構參數下的顫振速度，也就必須不斷地調用CFD求解器，計算量極大；此外，在考慮到氣動彈性問題的不確定性設計中，同樣會面臨計算量巨大的挑戰。

為解決這個問題，文獻[20]提出了一種適用于任意振型的非定常氣動力降階方法(ROM suitable for Arbitrary Mode Shapes, ROM-AMS)。首先尋找一組數學意義上的基模態振型，這些基模態振型以正確的系數線性疊加，可以復現出真實振型。文獻[20]中的基模態振型為一組分布在機翼平面上具有不同中心位置的徑向基函數。之后在基模態坐標下，構建基振型的非定常氣動力模型，在基模態空間和模態空間之間變換后，該模型就可以取代非定常CFD求解器，進而用于顫振分析。同時，該模型繼承了之前ROM在較寬頻率內對不同模態頻率的適應能力。在保證精度的前提下，該方法計算量僅為秒級。

然而，上述方法使用基振型數量較多，在模型訓練和辨識中會消耗較多時間，并且對于高階振型或復雜外形的擬合精度不足，可能導致顫振速度誤差放大。對此，本文利用主成分分析(PCA)方法來構建基振型。首先選取若干具有代表性的結構樣本，通過PCA分析得到基振型，同文獻[20]一樣，這里的基振型僅具有數學意義。分析表明，只需要很少的基振型就能達到較高精度的擬合，減少了計算量。之后，沿用文獻[20]的思路，構建適用于不同結構參數的非定常氣動力降階模型。

1 非定常氣動力降階模型

1.1 適用于給定振型的非定常氣動力降階模型

首先選擇可能發生顫振耦合的前n階法向振型Φ1(p)，Φ2(p)，…，Φn(p)，p為有限元節點坐標。為每階振型設計激勵信號ξ1，ξ2，…，ξn，之后調用CFD求解器，并使物面邊界網格按給定的運動形式做強迫運動，運動形式為

(1)

求解該運動形式下流場的前階氣動力響應(振型的廣義氣動力系數)F1，F2，…，Fn：

(2)

式中：p為當地壓強；q為來流動壓；ds為面積微元。于是得到了用于訓練氣動力模型的激勵響應數據對。之后選擇離散型多輸入多輸出差分模型建立基于振型的非定常氣動力降階模型：

(3)

式中：k′為時間步；F為系統輸出向量(n階廣義氣動力系數)；ξ為系統輸入向量(n階廣義位移)；Ai和Bi為待辨識矩陣；na和nb為由用戶決定的模型延遲階數。利用獲得的訓練數據，通過最小二乘方法求出式(3)中的待辨識矩陣，建立基于振型的非定常氣動力降階模型。

由于必須事先給定振型，因此，式(3)中的模型被稱為適用于給定結構(即給定振型)的非定常氣動力降階模型，即ROM-PMS，將該模型應用于顫振分析(見1.4節)，可以快速預測機翼的顫振特性。但當模態振型隨內部結構改動而發生改變時，就需重新調用CFD求解器采集訓練數據，并建立基于新模態振型的氣動力模型，這使得在氣動彈性優化設計和氣動彈性不確定性設計等應用中，ROM-PMS方法的計算量依然巨大。因此，需設法建立適用于任意振型的非定常氣動力降階模型，即ROM-AMS。

1.2 構建基振型

文獻[20]用徑向基函數法生成基振型，見圖1。如圖2所示，在機翼平面上選擇若干節點，每個節點上設置一個徑向基函數。按照正確的系數線性疊加后，這些徑向基函數就能擬合出完整的模態振型。當結構改變引起振型改變時，只需要修正疊加系數，就能擬合出新的振型，而徑向基函數本身不變。于是，在某個節點處按照圖1形狀隆起的機翼平面就可以作為基振型。不同基振型在不同的節點處隆起，顯然，節點越密集，所需基振型越多，擬合精度越高。

為保證擬合精度，該方法需要較多的基振型，即便如此，高階模態或復雜氣動外形擬合精度依然不足。因此，本文使用PCA方法生成基振型。

圖1 機翼表面徑向基函數Fig.1 Radial basis function of wing surface

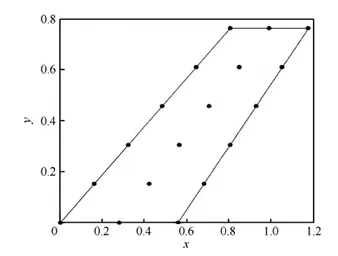
圖2 機翼表面節點分布Fig.2 Locations of basis points of wing surface

首先，在設計變量構成的空間內進行抽樣，得到n個結構樣本，進行模態分析后，每個樣本取前k階模態振型，于是得到了kn個振型Φi(p)，i=1,2,…,kn，并將其作為PCA分析的輸入向量。分析完成后，取對應特征值較大的前m個特征向量作為基振型φi(p)，i=1,2,…,m，m的大小取決于擬合精度要求。相比于徑向基函數法，PCA方法所需基振型數量很少，擬合精度高，但需要在優化開始前在變量空間內進行抽樣，并且抽樣質量會影響擬合效果。

1.3 適用于任意振型的非定常氣動力降階模型

記某結構的j階模態振型為Φj(p)，其中j=1,2,…,k,k為需要分析的模態總階數。Φj(p)可用基振型φi(p)表示為

(4)

式中：γij為用來擬合j階模態振型的第i個基振型的疊加系數。該系數實際上就是振型向量在基振型坐標下各軸上的投影。

之后用經典的氣動力降階方法建立基振型的ROM。首先為每個基振型設計激勵信號，這里的信號需要有足夠寬的頻帶。基振型乘以相應的激勵信號，相加得到激勵過程中動網格的變動位移。這里同樣使用ARX模型建立非定常氣動力降階模型

(5)

式中：t為時間步；f為輸出量，即基模態廣義氣動力系數；u為輸入量，即基模態廣義位移。調用CFD求解器得到各階基模態的響應后，即可通過最小二乘法得到式(5)中的待辨識矩陣。

需要注意，當前的氣動力模型只能由基模態的廣義位移計算出關于基模態的廣義氣動力系數，若要用于任意結構的顫振分析，氣動力模型還必須包含兩步轉化：

1) 將廣義位移轉化為基廣義位移(對應圖3中的Transformation 1)。

已知某機翼的k階模態振型Φ1(p),Φ2(p),…,Φk(p)，以及對應的k個廣義位移ξ1,ξ2,…,ξk，式(1)重寫為

(6)

將式(4)代入式(6)，得

(7)

式中：

(8)

其中：u1,u2,…,um被定義為基廣義位移，輸入到基振型ROM中。

2) 將基廣義氣動力系數轉化為廣義氣動力系數(對應圖3中的Transformation 2)。

基模態的廣義氣動力系數定義為

(9)

得到關于基振型的響應f1,f2,…,fm后，按式(10)轉化為真實模態的廣義氣動力響應F1,F2,…,Fk：

(10)

上述兩步轉化的實質是輸入與輸出在模態坐標系和基模態坐標系之間的變換，這使得氣動力模型具備了由廣義位移計算出真實振型的廣義氣動力系數的能力。而當結構發生變動時，僅僅是式(8)和式(10)中的系數發生變化，因此，ROM-AMS能極大提升氣動彈性優化設計和不確定性分析的效率。具體流程圖見圖3。

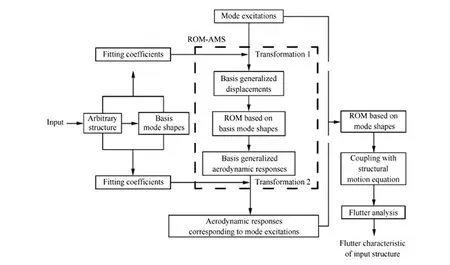
圖3 ROM-AMS的顫振分析流程Fig.3 Flowchart of flutter analysis through ROM-AMS

1.4 顫振分析方法

將氣動力模型轉化為連續形式的狀態空間方程，得

(11)

在模態坐標系下，結構運動方程為

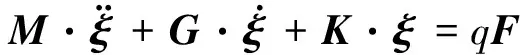
(12)

式中：M、G、K由該結構的有限元分析結果確定。將式(12)轉化為連續型狀態空間方程

(13)

式中：xa和xs為狀態空間變量；Aa、As、Ba、Bs、Ca、Cs、Da和Ds均為狀態空間方程矩陣。

耦合式(11)和式(13)，得到氣動彈性系統的狀態空間方程

(14)

這樣，氣動彈性系統的穩定性分析可轉化為求解系統穩定性判斷矩陣A的特征值問題。通過求解不同動壓下A的特征值，制成v-g圖和v-ω圖，進而研究機翼的顫振特性。具體的推導過程見文獻[6]。

2 算 例

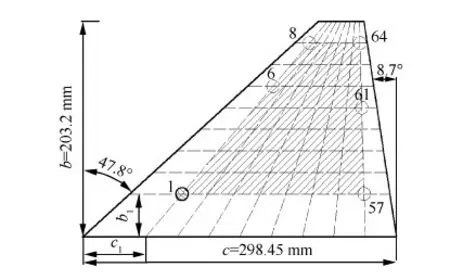
圖4 切尖三角翼試驗模型和配重掛載位置Fig.4 Clipped delta wing test model and positions of concentrated mass

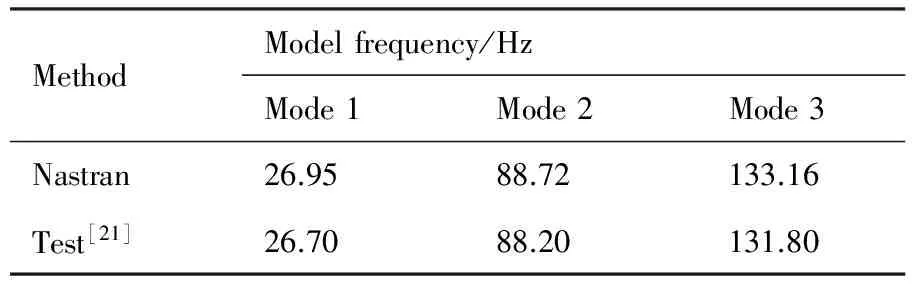
表1 原試驗模型的模態頻率Table 1 Modal frequency of original test model

選擇切尖三角翼試驗模型作為研究算例[21]，通過掛載配重并改變其位置來模擬結構的變化。如圖4所示，機翼的二元板結構被圓形實線分割成兩個部分：圓形的配重和機翼其余部分。圖中c為弦長，b為展長。配重的圓心位置由弦向和展向的虛線交叉確定，通過改變虛線位置參數b1和c1進而改變配重的位置。配重質量約為0.1 kg，機翼其余部分質量約為0.24 kg。表1對比了原試驗模型模態頻率f的Nastran數值解和試驗解[21]，說明Nastran進行結構分析精度足夠。圖5對比了樣本6和樣本61的前兩階模態振型，可以看到，配重位置的改變會對振型產生較大影響，而后兩階振型變化更大，限于篇幅并未展示。這樣的改變程度足以模擬工程中的復雜結構變動帶來的振型變化。

首先需要找出一組基振型，使得無論將配重掛載于圖4陰影區域的哪個位置，對應結構的前4階模態振型都能由基振型線性疊加擬合得到。如圖4所示，改變b1和c1生成64個掛載點各異的樣本。例如，6號結構的掛載點位于陰影區域左側邊線(標有“6”的位置)，61號結構的掛載位置為該區域右側邊線。獲得這些樣本結構的前4階振型后，進行PCA分析，選取對應特征值較大的前6個特征向量作為基振型，如圖6所示。

為了表征基振型擬合實際振型的精度，這里引入MAC(Modal Assurance Criteria)值[20]。

圖5 典型結構的前2階模態振型云圖Fig.5 The first 2 mode contour of vibration shapes of typical structures

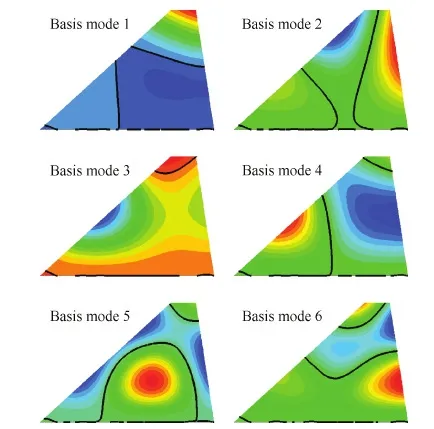
圖6 前6階基模態振型Fig.6 Mode vibration shapes of first 6 basis modes

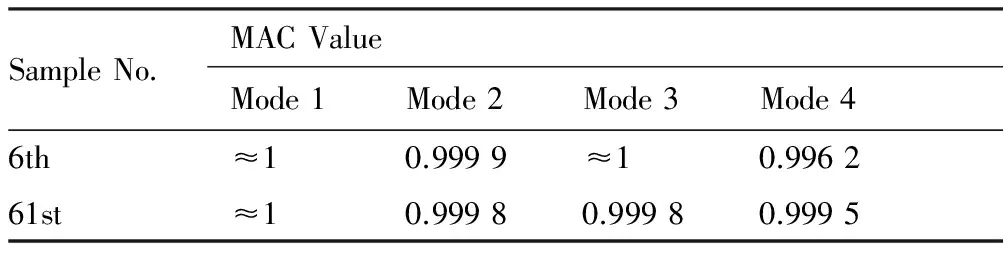
表2 樣本6和樣本61的MAC值Table 2 MAC value of the 6th and the 61st samples

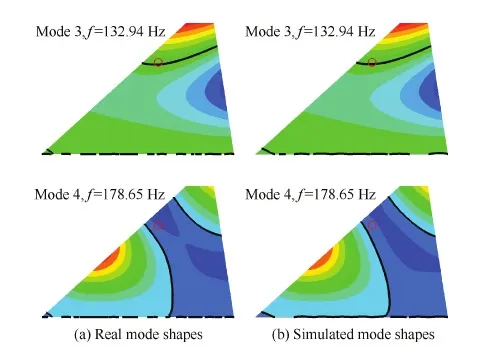
圖7 樣本6的3、4階模態振型Fig.7 The 3rd and 4th mode of vibration shapes of the 6th sample

式(15)中，Φ*為基模態擬合出的振型，Φ為對應的真實振型。MAC值越接近1，表示擬合精度越高。基振型的擬合效果見表2和圖7。由于3、4階振型擬合難度更大，故圖7僅顯示3、4階振型以說明問題。

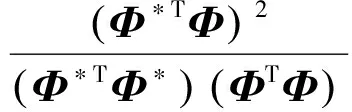
(15)

圖8為基振型數量對擬合精度的影響。以樣本6為例，可以看到，當基振型選取數量少于4時，各階振型擬合精度依然不足，尤其是高階振型，由于其形狀復雜，擬合精度更差。但隨著選取基模態階數的增加，4階模態都達到了較高精度，僅選取4個基模態時，4階振型的MAC值就已經接近1，這種效果是徑向基函數(RBF)方法難以達到的。算例選取了前6階基振型，因此擬合精度足夠。

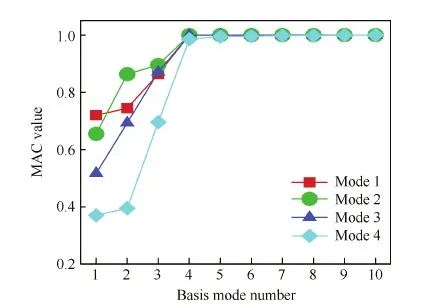
圖8 基振型選取數量對MAC值的影響(樣本6)Fig.8 Influence of selected basis mode number on MAC value (the 6th sample)

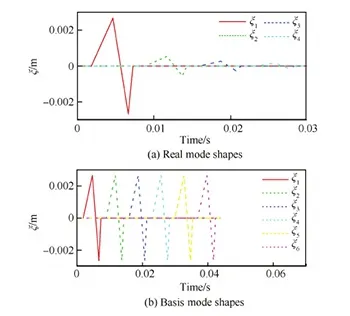
圖9 真實模態和基模態振型的激勵信號Fig.9 Excitations signal of real mode shapes and basis mode shapes

之后驗證ROM-PMS的準確性。使用圖9(a)中的信號激勵原試驗模型的前4階模態，用CFD求解Ma=0.87，來流密度為0.41 kg/m3時各階對應的廣義氣動力。顫振動壓實驗值為16 548 Pa[22]，而ROM-PMS結果為17 155 Pa，相對誤差僅為3.66%。

采用與ROM-PMS相同的流場條件，建立基振型的ROM。使用圖9(b)的信號激勵6階基模態，得到廣義氣動力響應后，訓練ARX模型，輸出輸入延遲階數均為12。圖10表明，ROM-AMS獲得的廣義氣動力系數響應具有較高的精度。

算例使用了7個參考樣本來驗證求解精度，如圖11所示。使用ROM-AMS方法得知，樣本6 和樣本61分別為顫振臨界速度最大和最小的樣本。圖12和表3對比了ROM-AMS和ROM-PMS進行顫振分析的結果，說明ROM-AMS方法具有較高的精度。最后，通過ROM-AMS方法得出的掛載點位置對顫振速度的影響如圖13所示。

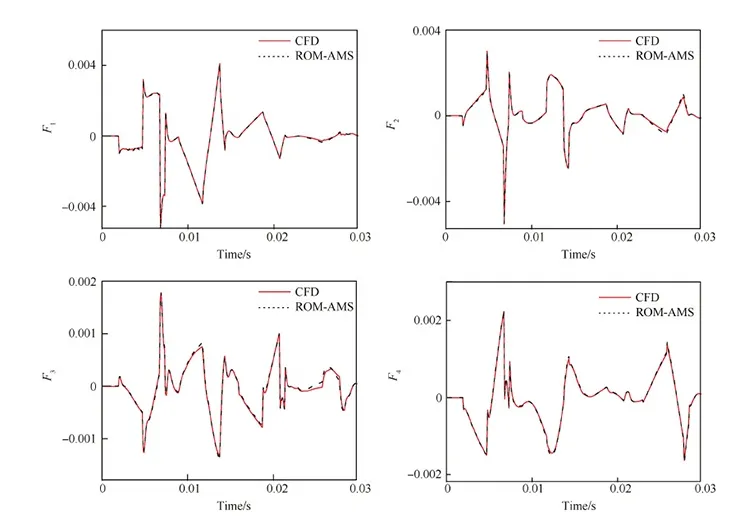
圖10 樣本6對應于圖9(a)中激勵的氣動力響應Fig.10 Aerodynamic responses corresponding to mode excitations presented in Fig.9(a) for the 6th sample

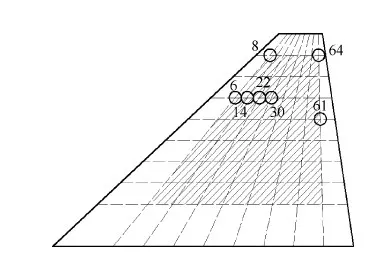
圖11 參考樣本的掛載點位置Fig.11 Positions of concentrated mass of reference samples

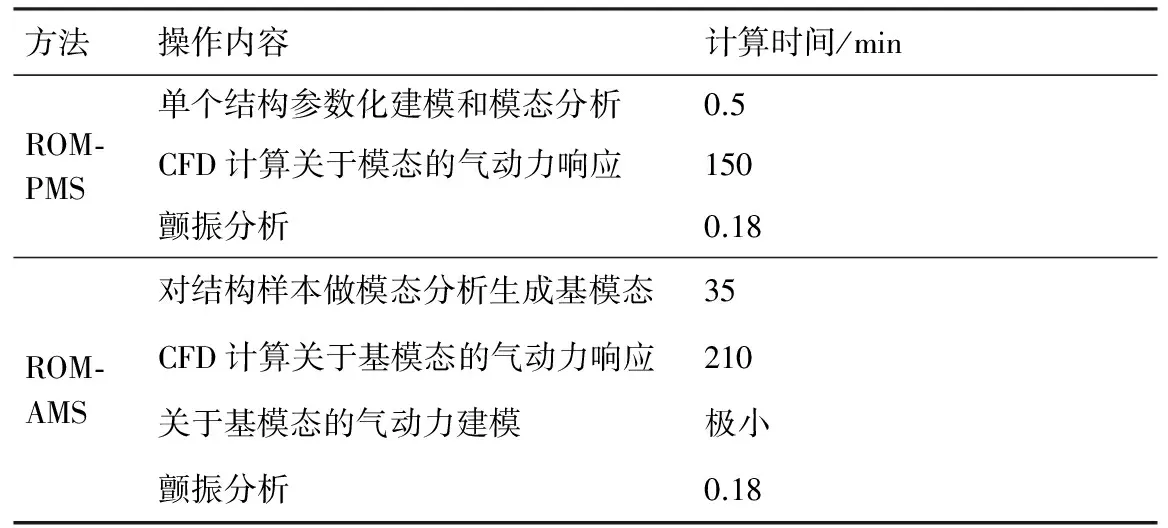
以上算例均在具有8核CPU、3.6 GHz主頻和8 G內存的工作機上運行，計算時間對比如表4 所示。可以看到，在計算單個結構的顫振特性時，ROM-AMS方法要比ROM-PMS方法多約60%的計算量，但如果需要計算1 000個結構，ROM-PMS方法需要消耗大約2 500 h，即104.1 d，而ROM-AMS僅需約15.5 h，因此，ROM-AMS方法適用于需要分析大量結構的氣動彈性優化設計和不確定性設計。

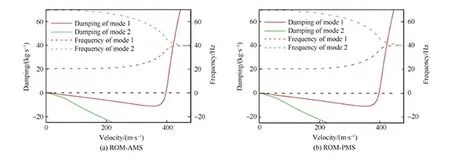
圖12 樣本6的顫振分析結果Fig.12 Flutter analysis results for the 6th sample

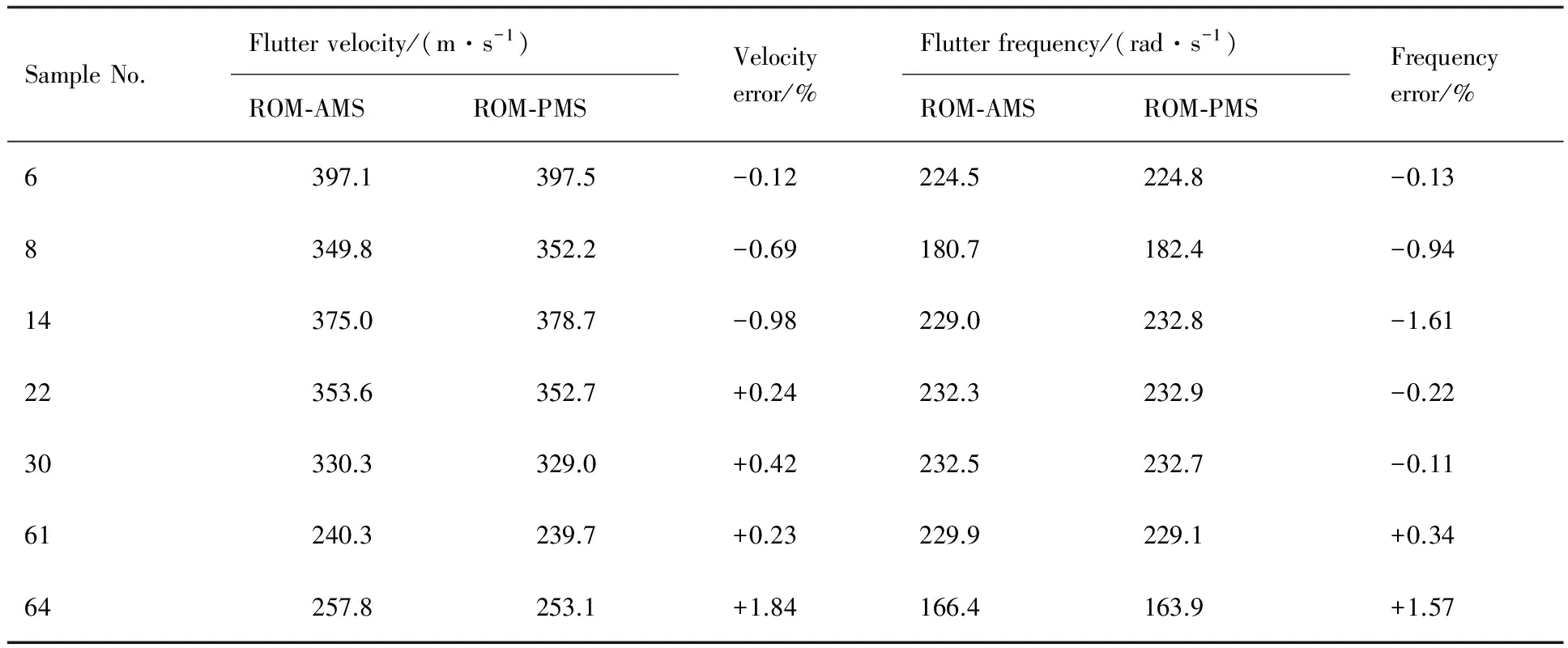
表3 ROM-AMS與ROM-PMS方法結果對比Table 3 Comparison of solutions of ROM-AMS and ROM-PMS methods

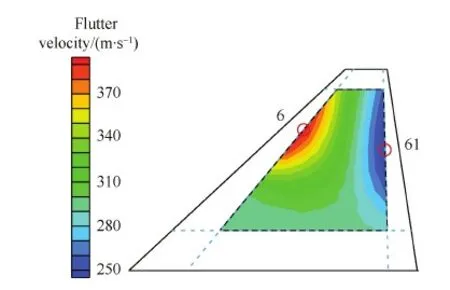
圖13 掛載點位置對顫振速度的影響Fig.13 Influence of concentrated mass position on flutter velocity

表4ROM-AMS和ROM-PMS方法顫振分析的計算時間

Table4ComputationalcostofROM-AMSandROM-PMSmethodsflutteranalysis

方法操作內容計算時間/minROM?PMS單個結構參數化建模和模態分析0．5CFD計算關于模態的氣動力響應150顫振分析0．18ROM?AMS對結構樣本做模態分析生成基模態35CFD計算關于基模態的氣動力響應210關于基模態的氣動力建模極小顫振分析0．18

3 結 論

1) 相比于徑向基函數法，PCA方法擬合抽樣空間內任意結構振型尤其是高階振型精度更高，同時使用基振型數量較少。

2) ROM-AMS不僅繼承了之前降階方法對模態頻率在較寬頻域內變化的適應能力，同時也能適應振型的較大變化，因此具有相同氣動外形下變結構的適應能力。

3) 適用于任意模態振型的氣動力建模方法，能夠快速準確地得到優化范圍內任意結構的顫振特性，且求解的顫振速度和頻率精度較高。

綜上，本文提出的氣動力建模方法能夠適用于變動參數的不同結構，為之后的氣動彈性優化設計和氣動彈性不確定性設計打下了基礎。

[1] DOWELL E H, HALL K C. Modeling of fluid-structure interaction[J]. Annual Review of Fluid Mechanics, 2001, 33(1): 445-490.

[2] LUCIA D J, BERAN P S, SILVA W A. Reduced-order modeling: New approaches for computational physics[J]. Progress in Aerospace Sciences, 2004, 40(1-2): 51-117.

[3] 張偉偉, 葉正寅. 基于CFD的氣動力建模及其在氣動彈性中的應用[J]. 力學進展, 2008, 38(1): 77-86.

ZHANG W W, YE Z Y. On unsteady aerodynamic modeling based on CFD technique and its applications on aeroelastic analysis[J]. Advances in Mechanics, 2008, 38(1): 77-86 (in Chinese).

[4] 陳剛， 李躍明. 非定常流場降階模型及其應用研究進展與展望[J]. 力學進展, 2011, 41(6): 686-701.

CHEN G, LI Y M. Advances and prospects of the reduced order model for unsteady flow and its application[J]. Advances in Mechanics, 2011, 41(6): 686-701 (in Chinese).

[5] 張偉偉, 葉正寅. 操縱面對跨聲速機翼氣動彈性特性的影響[J]. 航空學報, 2010, 66(7): 999-1007.

ZHANG W W, YE Z Y. Effect of control surface on airfoil flutter in transonic flow[J]. Acta Aeronautica et Astronautica Sinica, 2010, 66(7): 999-1007 (in Chinese).

[6] ZHANG W W, YE Z Y. Reduced-order-model-based flutter analysis at high angle of attack[J]. Journal of Aircraft, 2007, 44(6): 2086-2089.

[7] ZHANG W W, YE Z Y. Control law design for transonic aeroservoelastic[J]. Aerospace Science and Technology, 2007, 11(2-3): 136-145.

[8] DOWELL E H, THOMAS J P, HALL K C. Transonic limit cycle oscillation analysis using reduced order aerodynamic models[J]. Journal of Fluids and Structures, 2004, 19(1): 17-27.

[9] BERAN P S, LUCIA D J, PETTIT C L. Reduced-order modeling of limit-cycle oscillation for aeroelastic systems[J]. Journal of Fluids and Structures, 2004, 19(5): 575-590.

[10] JONES D P, ROBERTS I, GAITONDE A L. Identification of limit cycles for piecewise nonlinear aeroelastic systems[J]. Journal of Fluids and Structures, 2007, 23(7): 1012-1028.

[11] ZHANG W W, WANG B B, YE Z Y, et al. Efficient method for limit cycle flutter analysis by nonlinear aerodynamic reduced-order models[J]. AIAA Journal, 2012, 50(5): 1019-1028.

[12] MANNARINO A, MANTEGAZZA P. Nonlinear aeroelastic reduced order modeling by recurrent neural networks[J]. Journal of Fluids and Structures, 2014, 48: 103-121.

[13] 寇家慶, 張偉偉, 葉正寅. 基于分層思路的動態非線性氣動力建模方法[J]. 航空學報, 2015, 36(12): 3785-3797.

KOU J Q, ZHANG W W, YE Z Y. Dynamic nonlinear aerodynamics modeling method based on layered model[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(12): 3785-3797 (in Chinese).

[14] KOU J Q, ZHANG W W. An approach to enhance the generalization capability of nonlinear aerodynamic reduced-order models[J]. Aerospace Science and Technology, 2016, 49: 197-208.

[15] ZHANG W W, KOU J Q, WANG Z Y. Nonlinear aerodynamic reduced-order model for limit-cycle oscillation and flutter[J]. AIAA Journal, 2016, 54(10): 3302-3310.

[16] WANG Z C, ZHANG Z C, LEE D H, et al. Flutter analysis with structural uncertainty by using CFD-based aerodynamic ROM[C]//49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Reston: AIAA, 2008.

[17] SONG S F, LU Z Z, ZHANG W W, et al. Uncertainty importance measure by fast fourier transform for wing transonic flutter[J]. Journal of Aircraft, 2011, 48(2): 449-455.

[18] MARQUE S, BADCOCK K J, KHODAPARAST H H, et al. Transonic aeroelastic stability predictions under the influence of structural variability[J]. Journal of Aircraft, 2010, 47(4): 1229-1239.

[19] MARQUE S, BADCOCK K J, KHODAPARAST H H, et al. How structural model variability influences transonic aeroelastic stability[J]. Journal of Aircraft, 2012, 49(5): 1189-1199.

[20] ZHANG W W, CHEN K J, YE Z Y. Unsteady aerodynamic reduced-order modeling of an aeroelastic wing using arbitrary mode shapes[J]. Journal of Fluids and Structures, 2015, 58: 254-270.

[21] SCHAIRER E T, HAND L A. Measurements of unsteady aeroelastic model deformation by stereo photogrammetry[J]. Journal of Aircraft, 1999, 36(6): 1033-1040.

[22] GORDNIER R E. Computation of limit-cycle oscillations of a delta wing[J]. Journal of Aircraft, 2003, 40(6): 1206-1208.

(責任編輯： 李明敏)

Unsteady aerodynamic reduced-order modeling method forparameter changeable structure

WANGZiyi,ZHANGWeiwei*

SchoolofAeronautics,NorthwesternPolytechnicalUniversity,Xi’an710072,China

Computational fluid dynamics (CFD) based unsteady aerodynamic reduced-order model (ROM) can make significant improvement of efficiency of transonic aeroelastic analysis. However, the existing ROM is applicable only to structures with fixed parameters, namely prescribed model shapes (ROM-PMS). When structural parameters should be altered such as structure optimization and uncertainty analysis, ROM-PMS is no longer feasible. To settle the problem, a new unsteady aerodynamic modeling method for arbitrary model shapes is developed based on Ref.[20]. Parametric sampling and modal analysis are conducted on the structure to be designed and analyzed. The basic mode shapes are then obtained through principal component analysis (PCA). Real model shapes of arbitrary structure in the sample space can be synthesized by linearly superimposing basic mode shapes with correct coefficients. The coefficients of superposition change with the alteration of structure parameters. The analysis shows that just small number of basic modes can reach desirable accuracy. Classical modeling method can be used to construct ROM in basic mode shape coordinate. The ROM applicable for various structures can be developed from ROM in basic mode coordinate, which means that structural parameters can be arbitrarily altered in the sample space, while ROM is universal. This method can be widely applied to aeroelastic optimization design and uncertainty analysis, with great improvement in computational efficiency.

structure optimization; parameter variation; reduced-order model (ROM); transonic flow; flutter; unsteady aerodynamics

2016-10-01；Revised2016-11-21；Accepted2017-01-05；Publishedonline2017-01-091550

URL：www.cnki.net/kcms/detail/11.1929.V.20170109.1550.008.html

s：NationalNaturalScienceFoundationforExcellentYoungScholar(11622220);SeedFoundationofInnovationandCreationforGraduateStudentsinNorthwesternPolytechnicalUniversity(z2016002)

2016-10-01；退修日期2016-11-21；錄用日期2017-01-05； < class="emphasis_bold">網絡出版時間

時間：2017-01-091550

www.cnki.net/kcms/detail/11.1929.V.20170109.1550.008.html

國家自然科學基金優秀青年基金 (11622220)； 西北工業大學研究生創意創新種子基金 (z2016002)

*

.E-mailaeroelastic@nwpu.edu.cn

王梓伊， 張偉偉． 適用于參數可調結構的非定常氣動力降階建模方法J． 航空學報,2017,38(6):220829.WANGZY,ZHANGWW.Unsteadyaerodynamicreduced-ordermodelingmethodforparameterchangeablestructureJ.ActaAeronauticaetAstronauticaSinica,2017,38(6):220829.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.120829

V211.3

A

1000-6893(2017)06-220829-10

*Correspondingauthor.E-mailaeroelastic@nwpu.edu.cn