RV減速器擺線齒輪熱分析

李威，胡岳龍

(北京科技大學 機械工程學院，北京 100083)

RV減速器擺線齒輪熱分析

李威，胡岳龍

(北京科技大學 機械工程學院，北京 100083)

為了提高RV(Rotate Vector)減速器的傳動能力及傳動精度，本文分析了RV減速器中擺線針輪傳動部分的傳動原理和齒廓形成，計算了擺線輪接觸齒面摩擦熱流量所需的各種參數，得出嚙合接觸區域的摩擦熱流量及對流邊界條件。通過三維建模，并運用有限元軟件Ansys Workbench進行分析，得出了擺線輪齒在實際傳動過程中的穩態溫度場分布，考慮了不同輸入功率和接觸區條形區域劃分數量對實際結果精度產生的影響，得出了最佳的條形區域劃分數量為32。為提高機構整體傳動精度、避免輪齒膠合、指導輪齒修形等更深入的研究奠定了基礎。

RV減速器； 擺線針輪傳動； 摩擦熱流量； 有限元分析； 溫度場； 條形區域

RV減速器以其體積小、速比大、運動精度高、回轉誤差小等優點被廣泛應用于機器人的關節處。作為RV減速器重要組成部分的擺線針輪傳動機構，對于RV減速器整體性能，尤其是傳動精度的影響是不容忽視的。擺線針輪傳動機構是由擺線輪與若干針齒相互嚙合傳動，在傳動過程中會產生摩擦熱，進而產生熱變形，從而對整體的傳動精度產生影響，甚至在嚙合處發生熱膠合。所以對擺線針輪傳動部分進行相關熱分析，對于提高RV減速器的整體傳動精度是十分必要的。

目前國內外對于擺線針輪傳動機構熱分析的相關研究還少有報道，但是對于齒輪以及行星齒輪系的溫度場及熱分析已經有學者進行了相關的研究，方法主要有解析法[1]、試驗方法[2-4]、有限元法[5-6]。解析法做了一定簡化，與工程實際往往相差較大；試驗法雖然可以得出比較準確的溫度值，但對設備要求較高，成本較大，適合科學研究，但缺乏通用性。有限元法仿真結果取決于準確的摩擦熱流量和對流邊界條件的施加，簡單有效。本文將在此基礎上，運用有限元的方法，將其應用于擺線針輪傳動機構上，通過理論計算分析得出溫度場，從而為后續的相關研究奠定基礎。

1 擺線針輪傳動原理及擺線輪齒廓的形成

RV減速器中擺線針輪傳動機構的傳動原理如圖1所示，擺線輪安裝在有一定偏心距的輸入軸上。當輸入軸轉動時，擺線輪不僅繞其自身自轉，同時還會隨著輸入軸一起繞著針齒輪中心公轉。所以在行星輪系中，把擺線輪稱為行星輪，而把相對固定的針齒輪稱為中心輪或太陽輪。針齒輪是由若干個針齒銷均勻分布固定在半徑為rp的圓周上，針齒銷上套有針齒套共同組成了針齒，擺線輪齒數比針齒數少一個，圖中針齒數為18個。

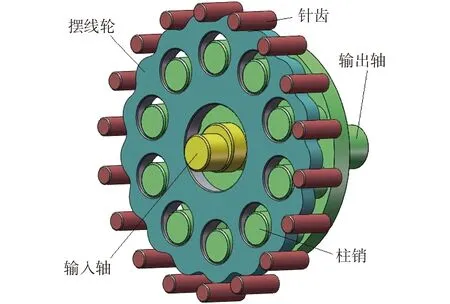
圖1 擺線針輪傳動機構Fig.1 The transmission of pin-cycloid planetary gearing

以擺線輪的幾何中心為原點，通過原點并以擺線輪齒槽的對稱軸所在直線為x軸，建立坐標系，可得擺線輪齒廓(即：短幅外擺線齒廓)的標準齒形方程式為[7]

(1)

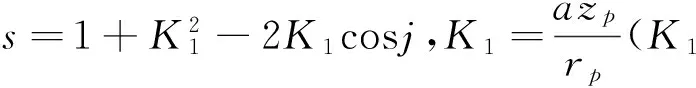
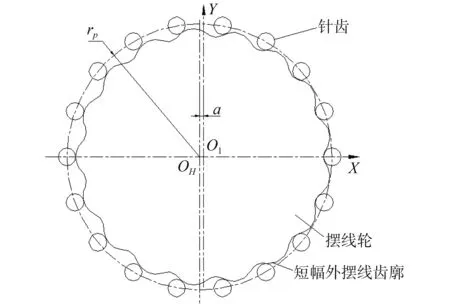
圖2 短幅外擺線齒廓Fig.2 The curtate epicycloid tooth profile

2 摩擦熱流量的計算

在擺線輪與針齒嚙合傳動中，它們的嚙合面處會產生大量的摩擦熱，這會導致擺線輪齒的溫度逐漸升高；然而又由于齒面潤滑油和空氣等其他因素，使擺線輪齒同時會散失熱量。最終，傳動中的擺線輪齒會達到一個熱平衡狀態，此時的溫度將不再發生劇烈的變化，稱為擺線輪齒的穩態溫度(也叫本體溫度)。

本文將通過有限元的方法模擬三維擺線輪在傳動過程中，輪齒嚙合處摩擦熱的產生及傳遞過程，并在相應位置施加對流邊界條件，進而求解計算獲得整個擺線輪齒的穩態溫度場分布。所選取的擺線針輪傳動模型參數如表1所示。

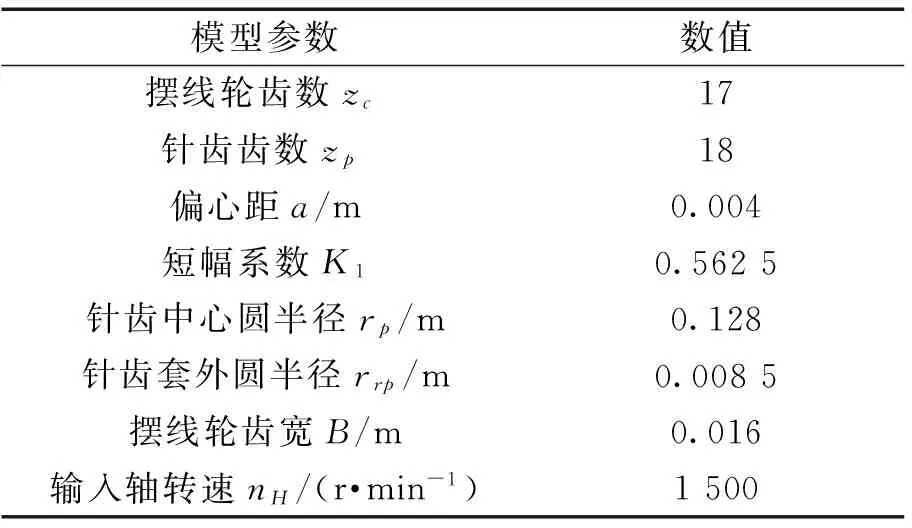
表1 模型主要參數

由于在傳動過程中，擺線輪齒每個齒的受載和傳熱、散熱情況基本相同，因此各個齒的穩態溫度場分布差別不大，所以可以建立單齒模型來分析整個擺線輪齒的穩態溫度場。

從擺線輪模型上切出一個輪齒如圖3，其接觸區域為輪齒的一半齒面[8](區域EFJH)。將接觸區域沿齒寬方向等分出若干條形區域并編號(0、1、2…31、32)，這里分出32個條形區域。其中的每一條等分線即為擺線輪齒與針齒在不同嚙合位置處的理論嚙合線，而每一條嚙合線的位置由上文中提到的嚙合相位角φ來決定(其對應關系如圖4)，嚙合線上的每一點即為它們的嚙合點。

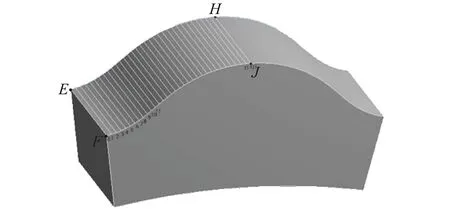
圖3 擺線輪齒模型Fig.3 The model of cycloidal gear tooth

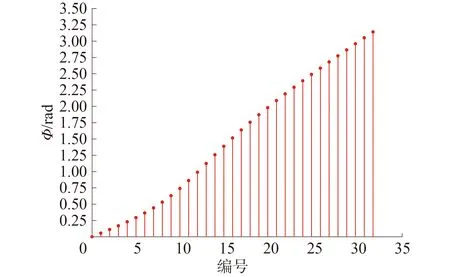
圖4 不同嚙合位置處的嚙合相位角Fig.4 The phase angles of meshing for different engaging positions

由擺線針輪傳動機構的傳動原理可知，擺線輪與針齒套接觸，針齒套與針齒銷接觸，它們兩兩之間均存在相對滑動和滾動。為了便于計算，這里假設針齒套與針齒銷固結在一起(下文統稱針齒，其半徑用rrp表示，即針齒半徑等于針齒套半徑)。因此，擺線輪齒與針齒嚙合處的摩擦熱主要由它們之間的相對滑動產生。

擺線輪齒與針齒不同嚙合處的摩擦熱流量q由它們之間的接觸應力σp、相對滑動速度vr、摩擦系數f和能量轉化系數γ決定[5，9-10]，計算公式為

q=spvrfg

(2)

對于σp、vr和f的求解過程將在下文中介紹，γ為摩擦能轉化為熱能的能量轉化系數，一般取0.9～0.95[6，11]。

2.1平均接觸應力σp

針齒齒廓為圓，擺線輪齒廓為曲線，擺線輪齒廓上各點的曲率半徑都不一樣。當針齒與擺線輪齒接觸并傳動時，可近似認為是兩個瞬時圓柱體在接觸。所以，擺線輪齒與針齒間的最大接觸應力σH及接觸區產生的寬度L可以根據Hertz公式來近似計算[8，12],其平均接觸應力σp為最大接觸應力σH的π/4倍[5，13-14]。

(3)

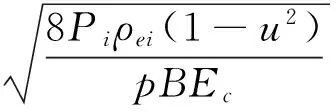
(4)

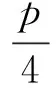
(5)

式中：Pi為擺線輪齒與針齒嚙合處的法向應力(i=0，1，2…32)；Ec為擺線輪齒與針齒嚙合處的當量彈性模量；B為擺線輪齒寬度；υ為擺線輪齒與針齒的泊松比(這里取0.3)；ρei為擺線輪齒與針齒嚙合處的當量曲率半徑(i=0，1，2…32)。

為了求得擺線輪齒與針齒嚙合的平均接觸應力σp，還需要求出它們在不同位置處的法向應力Pi、當量彈性模量Ec和當量曲率半徑ρei。

2.1.1 當量曲率半徑ρei

擺線輪標準齒形的理論齒廓曲線的曲率半徑ρ0i，由微積分公式可求得[8]

(6)

φi同上文φ，即不同的嚙合位置處(i=0，1，2…32)。實際齒廓曲線的曲率半徑ρi為[12]

(7)

針齒與擺線輪齒接觸點的當量曲率半徑ρei為[12]

(8)

由式(8)可知，當量曲率半徑的值是隨著φ的變化而變化，而φ值對應著擺線輪齒沿齒廓方向的嚙合位置，并且在相同的位置沿齒寬方向的值相同。擺線輪齒接觸區域的等分線處的當量曲率值可由圖5表示。

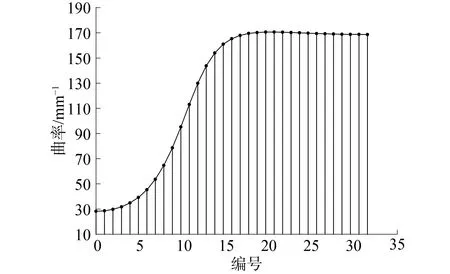
圖5 不同嚙合位置處的當量曲率Fig.5 The equivalent curvatures for different engaging positions

2.1.2 當量彈性模數Ec

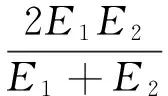
(9)

式中：E1、E2分別為擺線輪與針齒的彈性模數[12]。在擺線針輪傳動中，擺線輪與針齒(套)材料相同，且均為軸承鋼，所以有

Ec=E1=E2=2.06×105MPa

(10)

2.1.3 法向接觸壓力Pi

Pi為標準齒形下的擺線輪與針齒嚙合時的瞬時法向接觸壓力，其值為[8，15]

(11)

式中：Mv為擺線針輪傳動部分的輸出軸阻力矩。由式(11)可知，Pi的值也是隨著嚙合位置(即φ的值)的變化而變化，可由圖6表示。

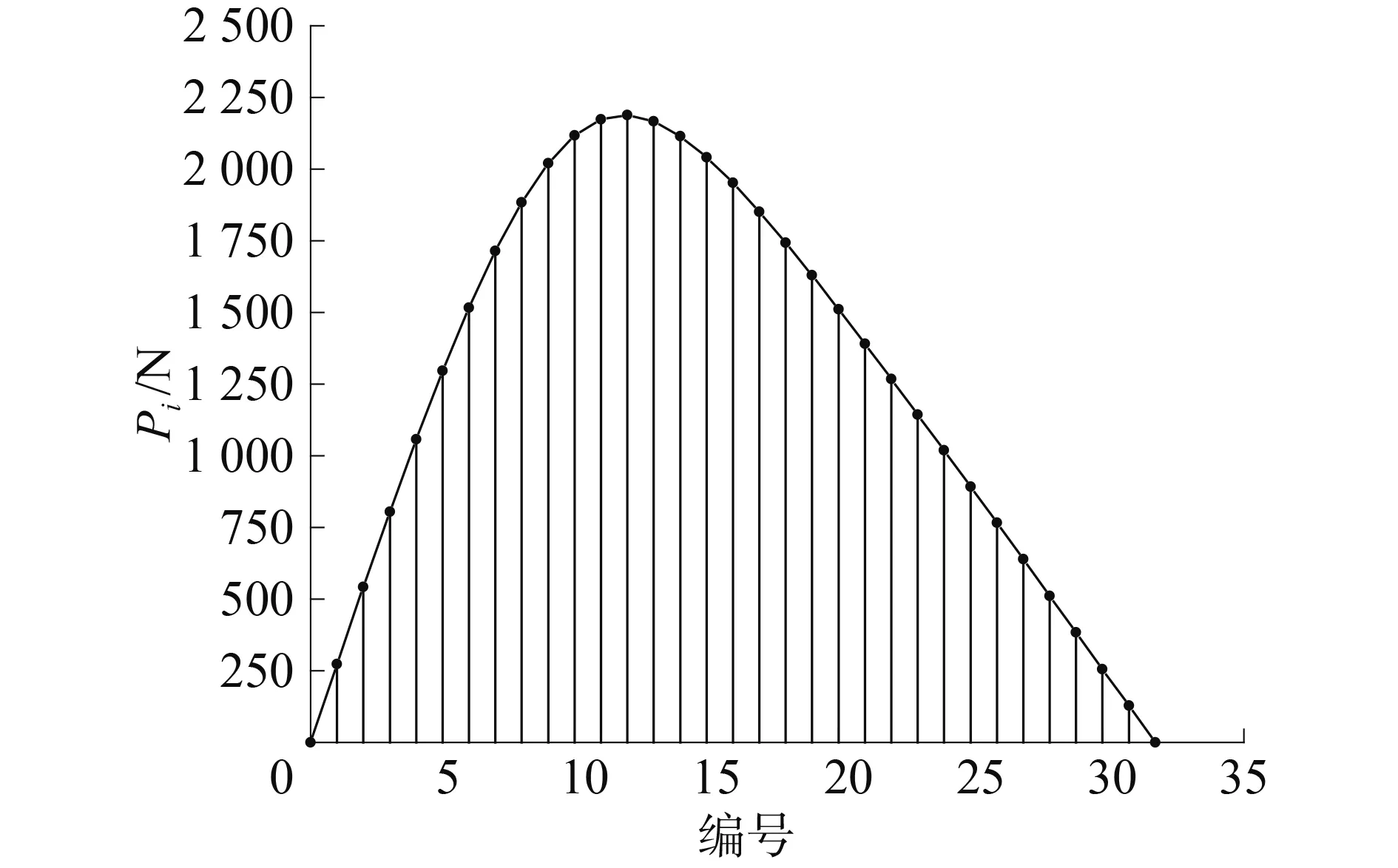
圖6 不同嚙合位置處的法向接觸壓力Fig.6 The normal contact pressure for different engaging positions

最終求出的在擺線輪齒接觸區域的平均接觸應力σp沿齒廓方向的值如圖7所示。其值沿擺線輪齒寬方向不發生變化，只是隨著嚙合線位置的不同，沿齒廓方向發生變化。

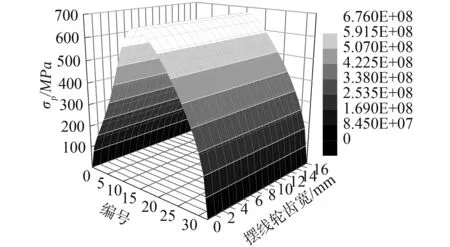
圖7 不同嚙合位置處的平均接觸應力Fig.7 The average contact stress for different engaging positions

2.2相對滑動速度vr

在擺線輪與針齒嚙合傳動過程中，擺線輪齒與針齒在嚙合線切線方向有相對滑動，產生相對滑動速度vr。本文已假設針齒套與針齒銷固結在一起并統稱針齒，所以針齒認為是固定不動的。正是因為vr的存在造成了擺線輪齒上摩擦熱的產生，其值如下[16-17]

(12)

式中：wH為擺線針輪傳動部分輸入軸的角速度；nH為擺線針輪傳動部分輸入軸轉速。負號表明擺線輪與輸入軸(轉臂)的轉向相反。

2.3摩擦系數f

擺線輪齒與針齒接觸處的摩擦系數f會受很多因素的影響，如材料、粗糙度、潤滑油特性等。所以可以采用實驗的方法具體測定某工作條件下的摩擦系數f。根據國內和國際上在齒輪膠合強度計算中采用的方法[9，18]，擺線輪齒與針齒嚙合位置處的摩擦系數f可表示為

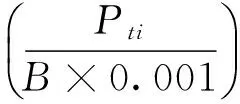
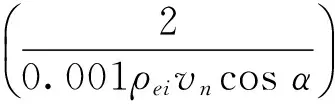
(13)

式中：X為擺線輪齒與針齒嚙合處的粗糙度因子；ρei為嚙合處的當量曲率半徑；η為潤滑油的動力粘度系數；Pti為嚙合處的切向載荷；vn為切向速度。

其中粗糙度因子X可表示為

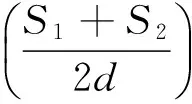
(14)

式中:S1、S2分別為擺線輪齒與針齒的表面粗糙度；d為擺線輪齒分度圓直徑。

為了得出擺線輪齒面的摩擦熱流量，分析計算其所需的各種參數，所得出的摩擦熱流量q的值如圖8所示。

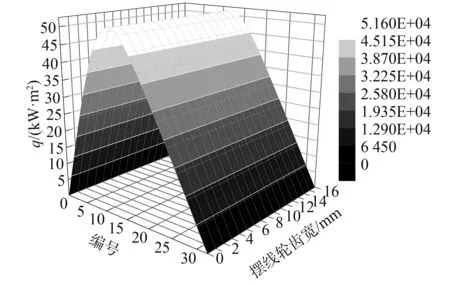
圖8 接觸齒面摩擦熱流量的分布Fig.8 The distribution of friction heat flux for contact tooth surface

3 對流換熱系數

在擺線輪與針齒嚙合傳動中，擺線輪齒同時和潤滑油以及空氣發生對流換熱而散失一部分熱量，其對流換熱系數的分析和計算目前還不是十分成熟，沒有一個較為精確的計算方法。由于擺線輪齒面和端面的對流換熱系數差別不大，在這里取它們相同，均以齒面與潤滑油及空氣的對流換熱系數h代替。h的計算方法可以參考對于齒輪齒面對流換熱系數的求法[9]。采用與參考文獻相同的潤滑油，其性能參數見表2。

(15)

式中：λ為導熱率，P為普朗特數，w為擺線輪自轉的角速度，v為運動粘度。

表2 潤滑油性能參數

4 擺線輪齒溫度場有限元分析

4.1擺線輪齒模型的建立和導入

用三維繪圖軟件Solidworks根據擺線輪齒廓的標準齒形方程式建立擺線輪的三維模型，并切出一個擺線輪齒導入到Ansys Workbench中，再進行擺線輪齒接觸區域條形區域的劃分，如第2章所述。同時在Workbench的此工程項目中設置好材料參數，并對此單齒模型進行網格劃分，如圖9所示。

圖9 擺線輪齒的網格劃分Fig.9 The mesh generation of the cycloidal gear tooth

4.2擺線輪齒摩擦熱流量的施加

對于擺線輪齒，由文中摩擦熱流量的求解過程可知，其值僅由于嚙合位置的不同沿著擺線輪齒齒廓方向發生變化，而在同一嚙合位置處沿齒寬方向沒有變化。所以，可在齒面平行于齒寬方向等分出若干條形區域，并將每條等分線編號，如圖3所示。再分別將每個條形區域兩側的等分線上的摩擦熱流量取平均值，將此平均值作為此條形區域的摩擦熱流量來施加。(例如：如圖3所示，分別求出1處和2處的摩擦熱流量，再取平均值，作為其間條形區域的摩擦熱流量)此等分線其實就是擺線輪齒與針齒的理論嚙合線，其上各點的摩擦熱流量是相同的(沿齒寬方向沒有變化)，其值等于此嚙合線上任一點的摩擦熱流量，可由上文摩擦熱流量的求解過程求出。

在這里需要特別注意的是，求出的摩擦熱流量是擺線輪齒與針齒嚙合傳動時，嚙合點在單位時間單位面積上產生的摩擦熱量。但在實際傳動中，此熱量并不是一個隨時間恒定不變的值，而是以一定時間t2為周期(此周期與擺線輪公轉有關)，周期性產生的。也就是說，在每一個周期內，擺線輪齒與針齒在每一條理論嚙合線上的嚙合點處只參與嚙合一次，也只有在這個短暫的嚙合時間段t1內，在此嚙合點處產生熱量q[6]。

在擺線輪與針齒的某處嚙合位置，其齒面接觸寬度L可由上文求得，所以在此位置產生摩擦熱流量的時間t1為

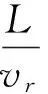
(16)

式中：vr為上文中的相對滑動速度。

由擺線輪與針齒嚙合傳動的原理可知，擺線輪繞針齒分布中心公轉的同時，也進行自轉，類似于行星輪系中的行星輪，并且擺線輪齒數比針齒數少一個。所以某一個擺線輪齒距下一次嚙合的時間周期t2等于擺線輪公轉(zp-1)個針齒所用的時間，其中zp、wH的含義同上文(wH為輸入軸角速度同時也是擺線輪繞針輪中心的公轉角速度)，則t2為

(17)

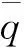
(18)

式中：q為擺線輪齒條形區域的摩擦熱流量；Λ為擺線輪與針齒嚙合的熱分配系數，這里近似取0.5[6]。針齒(銷套)在獲得熱量后溫度也會上升，但是由于其與擺線輪齒在某一嚙合位置的嚙合時間t1非常短暫，擺線輪齒的穩態溫度場受到的影響相對較小。

4.3擺線輪齒對流邊界條件的設定

在4.2節已經在接觸面EFJH上進行了摩擦熱流量的施加，這里再在齒廓曲面EFGI和輪齒的兩個側面FBCG、EADI上施加對流邊界條件，如圖10所示，其對流換熱系數值可由第3節求出。

4.4有限元計算分析

4.4.1 輸入功率對結果的影響

當擺線針輪傳動部分輸入功率分別為7.5、11.25、15 kW時，分析計算出的擺線輪齒溫度場分布如圖11所示。

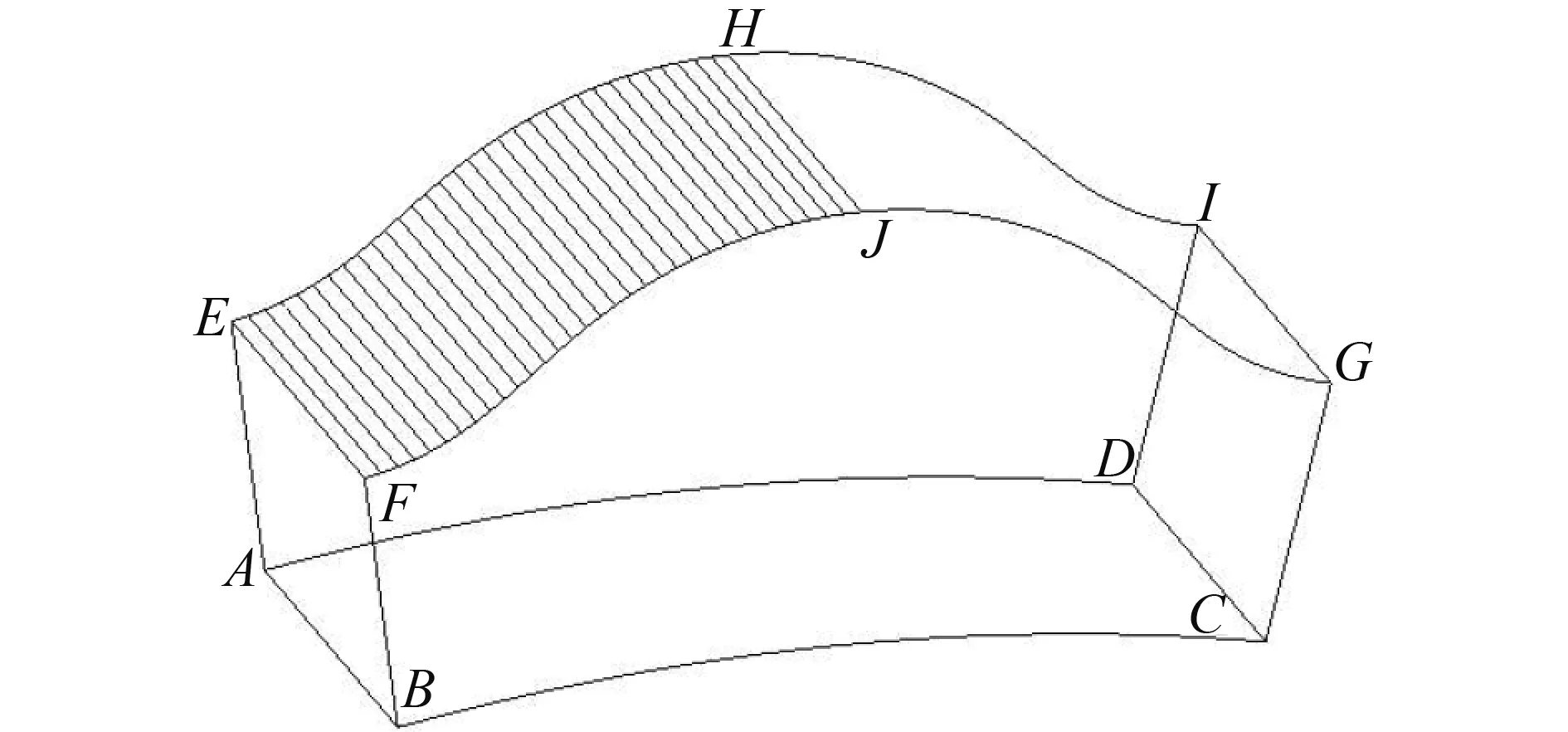
圖10 擺線輪齒Fig.10 The cycloidal gear tooth

由圖11可以看出，隨著輸入功率的增加擺線輪齒整體溫度上升，但擺線輪齒溫度分布規律大致不變；擺線輪齒接觸區域的最高溫度隨載荷的增加也顯著提高。這是因為隨著輸入功率的增加，擺線輪齒與針齒之間的摩擦熱流量也相應提高，導致溫度上升；但是對流換熱系數的影響相對較小，所以散熱狀況變化不大。這些均與實際情況相吻合。

擺線輪齒面從接觸區域一側到非接觸區域，溫度逐漸降低，形成了鮮明的溫度梯度；并且在輪齒接觸區域，齒面溫度整體高于齒體溫度。這是由于在接觸區域產生摩擦熱流量使齒面溫度上升，而在非接觸區域僅發生對流換熱降低了溫度所致。而正是這種溫度分布的不均勻性，嚴重減低了擺線針輪傳動部分以及整個RV減速器的傳動精度和承載能力，引起沖擊和振動，在實際傳動中需要進行充分考慮。

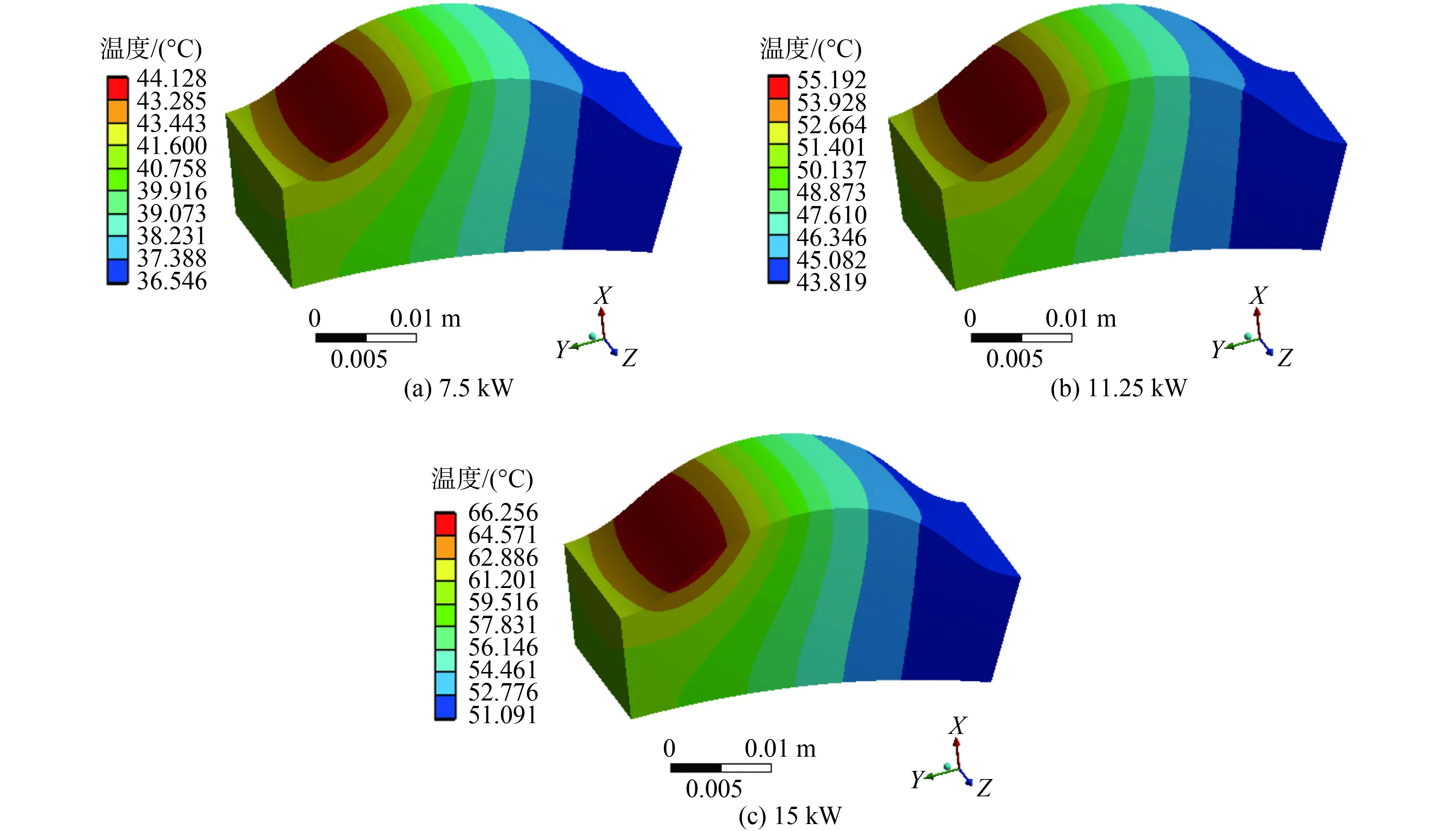
圖11 當輸入功率為7.5,11.25,15 kW時的溫度場分布Fig.11 The distribution of temperature fields when the input powers are 7.5, 11.25, 15 kW

擺線輪齒溫度場沿齒寬方向呈對稱分布，中間溫度偏高、兩端偏低，且最高溫度均出現在接觸區域靠中間的位置。這是由于在沿齒寬方向的嚙合線上，摩擦熱流量并未發生變化，它只是沿著齒廓方向隨著嚙合位置的不同而發生變化；并且擺線輪齒與潤滑油及空氣的對流邊界條件沿齒寬方向對稱分布，越靠近輪齒兩側對流換熱狀況越好，而越靠近中間狀況越差；擺線輪齒中間位置摩擦熱流量較大，散熱較小，所以最高溫度出現在擺線輪齒接觸面一側靠近中間的位置。而這種沿齒寬方向的溫度變化所產生的熱變形，將直接導致擺線輪齒與針齒嚙合接觸線長度的減少，降低傳動精度及承載能力。

4.4.2 條形區域劃分數量對結果精度的影響

考慮到上文中擺線輪齒面接觸區劃分的條形區域數量對最終結果可能產生的影響，在輸入功率為11.25 kW的情況下，分別劃分條形區域數為8、16、32、64，按上文方法進行計算分析，所得出的溫度場分布及最高溫度值如圖12所示。

由圖12可知，當擺線輪齒接觸區域劃分不同數量的條形區域時，溫度場分布規律大致不變，但整體溫度呈上升趨勢，齒面最高溫度和最低溫度的數值是不同的，但是隨著劃分區域數量的增加，溫度變化幅度越來越小，并且趨于平緩，其分布規律可由圖13表示。

由圖13溫度分布規律可以看到，當條形區域數為32時，擺線輪齒面最高溫度和最低溫度的變化開始趨于平緩，并且趨于恒定的數值，這個數值可以認為就是擺線輪齒的穩態溫度，因此所得出的溫度場分布結果較為精確。

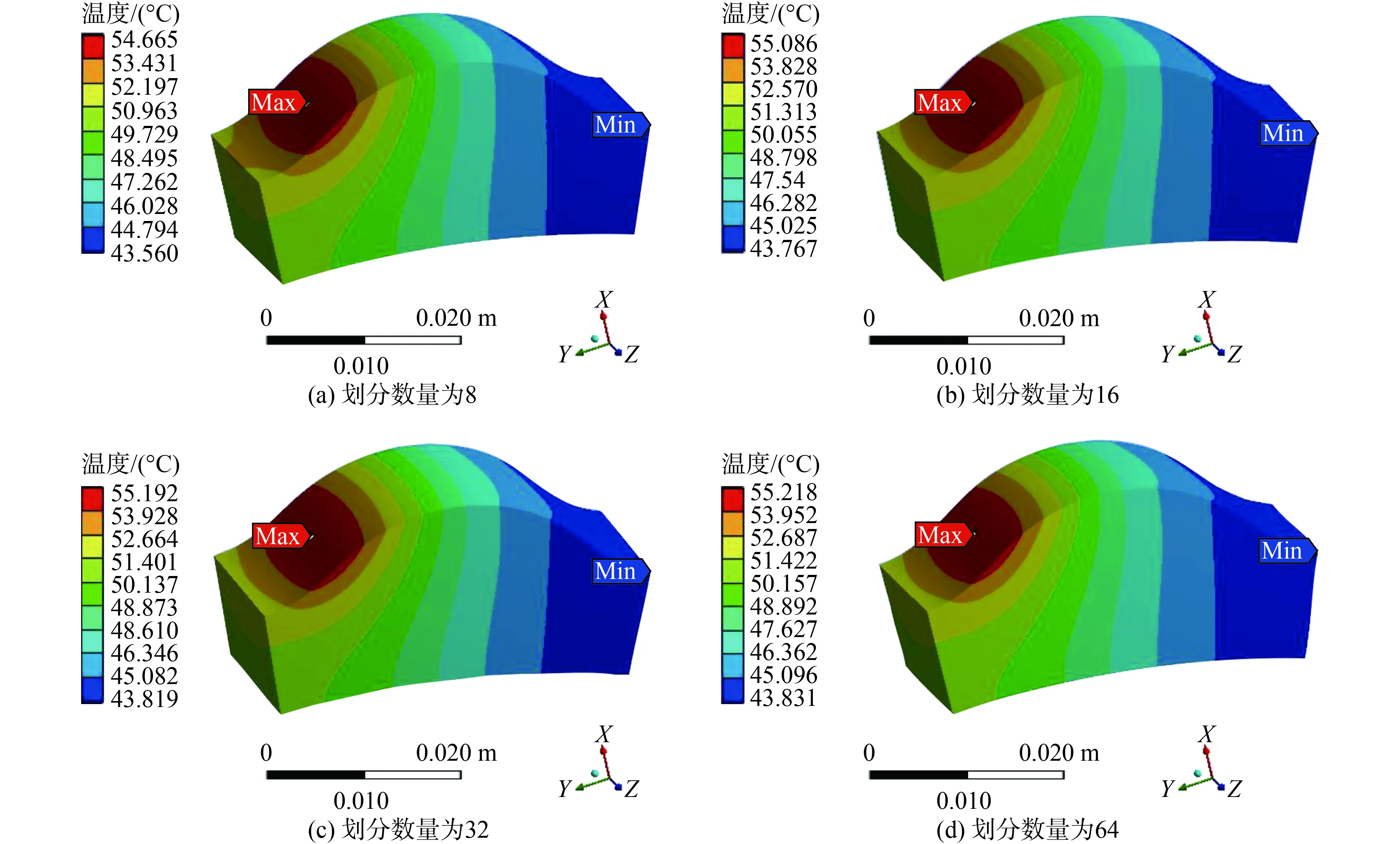
圖12 條形區域劃分數量為8、16、32、64的溫度場分布Fig.12 The number of bar area division are 8, 16, 32, 64

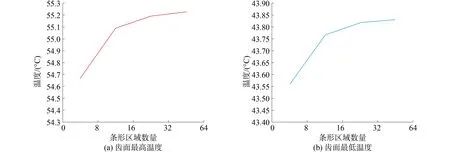
圖13 不同條形區域劃分時的溫度變化規律Fig.13 The temperature variation regularity for different bar area division

5 結論

1)驗證了隨著輸入功率的變化，擺線輪齒溫度場的變化規律與實際情況相吻合。

2)為了更加接近實際情況，充分考慮了摩擦熱流量的施加過程中，擺線輪齒接觸區條形區域的劃分數量對最終結果的影響，得出了更加準確的溫度場分布結果。

本文研究內容為今后的提高機構傳動精度、避免輪齒膠合、輪齒降溫、輪齒修形等更為深入的研究奠定了基礎。

[1] MAO K. A numerical method for polymer composite gear flash temperature prediction[J]. Wear, 2007, 262(11): 1321-1329.

[2] SUTTER G, RANC N. Flash temperature measurement during dry friction process at high sliding speed[J]. Wear, 2010, 268(11): 1237-1242.

[3] LETZELTER E, GUINGAND M, VAUJANY J P, et al. A new experimental approach for measuring thermal behaviour in the case of nylon 6/6 cylindrical gears[J]. Polymer testing, 2010, 29(8): 1041-1051.

[4] 趙建平, 杜鴻家. 艦船齒輪潤滑狀態研究[J]. 機械傳動, 1996(1)：70-71.

ZHAO Jianping, DU Hongjia.Research on lubrication modes of ship gears[J]. Journal of mechanical transmission,1996(1)： 70-71.

[5] 肖望強, 李威, 韓建友. 非對稱齒廓漸開線齒輪傳動的熱分析[J]. 農業機械學報, 2006, 37(12): 164-167.

XIAO Wangqiang, LI Wei, HAN Jianyou. Thermal analysis of involute gear transmission with unsymmetric tooth profile[J]. Transactions of the Chinese society for agricultural machinery, 2006, 37(12): 164-167.

[6] 龍慧, 張光輝, 羅文軍. 旋轉齒輪瞬時接觸應力和溫度的分析模擬[J]. 機械工程學報, 2004, 40(8): 25-26.

LONG Hui, ZHANG Guanghui, LUO Wenjun. Modeling and analysis of transient contact stress and temperature of involute gears[J]. Chinese journal of mechanical engineering, 2004, 40(8): 25-26.

[7] 何衛東, 李力行. 高精度 RV 減速器中擺線輪齒形的優化修形[J]. 大連鐵道學院學報, 1999, 20(2): 54-58.

HE Weidong, LI Lixing. The optimized modification of cycloidal gear of high precision RV reducer [J]. Journal of Dalian Railway Institute, 1999, 20(2):54-58.

[8] 鄭州工學院機械原理及機械零件教研室. 擺線針輪行星傳動[M]. 北京: 科學出版社, 1978: 64,74-75.

Department of mechanical engineering and mechanical parts in Zhengzhou Institute of Technology. The pin-cycloid planetary gearing[M]. Beijing: Science Press,1978,64: 74-75.

[9] 薛建華, 李威. 齒輪系統的溫度場預測方法[J]. 北京科技大學學報, 2014(2): 18.

XUE Jianhua, LI Wei. Prediction methods of gear system temperature fields[J]. Journal of University of Science and Technology Beijing, 2014(2): 18.

[10] LIN H T, LIN L K. Heat transfer from a rotating cone or disk to fluids of any Prandtl number[J]. International communications in heat and mass transfer, 1987, 14(3): 323-332.

[11] HANDSCHUH R F. Thermal behavior of spiral bevel gears[D]. Washington: Case Western Reserve University, 1993.

[12] 朱孝錄,何衛東,李威，等. 齒輪傳動設計手冊[M]. 北京: 化學工業出版社, 2004: 798, 772-773.

ZHU Xiaolu, HE Weidong, LI Wei,et al. Handbook of gear design[M]. Beijing: Chemical Industry Press, 2004: 798, 772-773.

[13] BLOK H. The thermal network method for predicting bulk temperatures in gear transmissions[C]∥Proc 7th Round Table Discussion on Marine Reduction Gears. Stal-Laval, Finspang, Sweden, 1969: 3-25.

[14] LONG H, LORD A, GETHIN D T, et al. Operating temperatures of oil-lubricated medium-speed gears: numerical models and experimental results[J]. Proceedings of the institution of mechanical engineers, Part G: Journal of aerospace engineering, 2003, 217(2): 87-106.

[15] 張東生, 關天民. 擺線針輪傳動動態受力分析理論[J]. 機械設計, 2006, 23(10): 35-37.

ZHANG Dongsheng, GUAN Tianmin. Dynamic force bearing analytical theory of cycloidal pinwheel transmission[J].Journal of machine design, 2006, 23(10): 35-37.

[16] 李充寧. 擺線針齒行星傳動輪齒的相對運動及滑動系數[J]. 機械傳動, 1998, 22(3): 19-21.

LI Chongning. Relative motion and sliding coefficient of gear teeth ofpin-cycloid planetary gearing[J]. Journal of mechanical transmission,1998, 22(3): 19-21.

[17] 機械系機械基礎實驗室. 關于擺線針輪行星傳動中幾個問題的討論[J]. 東北大學學報: 自然科學版, 1976(2): 84.

Mechanical basic laboratory. Discussion on several problems of thepin-cycloid planetary gearing [J]. Journal of Northeastern University: natural science, 1976(2): 84.

[18] BOBACH L, BEIICKE R, BARTEL D, et al. Thermal elastohydrodynamic simulation of involute spur gears incorporating mixed friction[J]. Tribology international, 2012, 48: 191-206.

本文引用格式：李威，胡岳龍. RV減速器擺線齒輪熱分析[J]. 哈爾濱工程大學學報， 2017， 38(10): 1560-1567.

LI Wei, HU Yuelong. Thermal analysis of cycloidal gear for the RV reducer[J]. Journal of Harbin Engineering University， 2017， 38(10): 1560-1567.

ThermalanalysisofcycloidalgearfortheRVreducer

LI Wei, HU Yuelong

(College of Mechanical Engineering, University of Science and Technology Beijing, Beijing 100083, China)

To improve the transmission capability and precision of the RV reducer, this paper analyzed the transmission principle and the tooth profile formation of pin-cycloid planetary gearing part for the RV reducer, calculated various parameters needed for the friction heat flux of the contact tooth surfaces of the cycloidal gear tooth, and obtained the friction heat flux and the convective boundary condition of the contact tooth surface. Through three-dimensional modeling and with the use of finite element analysis software ANSYS Workbench, this paper obtained the steady-state temperature field of the cycloidal gear tooth in the actual transmission process. Taking into account the effect of different input power and the number of bar area division in the contact tooth surface, this paper derived that the optimal number of bar area division is 32. This paper establishes the foundation for further research to improve the overall transmission accuracy of the mechanism, avoid tooth scuffing, and guide the tooth profile modification.

RV reducer; pin-cycloid planetary gearing; frictional heat flux; finite element analysis; temperature field; bar area

10.11990/jheu.201605085

http://www.cnki.net/kcms/detail/23.1390.U.20170816.1445.002.html

TH132.414

A

1006-7043(2017)10-1560-08

2016-05-25. < class="emphasis_bold">網絡出版日期

日期：2017-08-16.

國家自然科學基金項目(51275035);北京科技大學研究生教育發展基金項目(06400053).

李威(1967-), 男, 教授,博士生導師；胡岳龍(1989-), 男, 碩士研究生.

胡岳龍，E-mail：m17801024250@163.com.