基于熱載體焓?為判據的環冷機熱工參數仿真優化

張晟，馮軍勝，董輝

（東北大學國家環境保護生態工業重點實驗室，遼寧 沈陽 110819）

基于熱載體焓?為判據的環冷機熱工參數仿真優化

張晟，馮軍勝，董輝

（東北大學國家環境保護生態工業重點實驗室，遼寧 沈陽 110819）

以某冷卻面積為405 m2的環冷機為研究對象，基于多孔介質和局部非熱力學平衡理論，建立了環冷機二維穩態數值計算模型。借助 COMSOL軟件的自定義函數功能，將環冷臺車沿運行方向的移動速度定義到數值模型中，研究并分析影響燒結礦余熱回收的主要因素及其影響規律。以環冷機出口冷卻空氣的焓?作為參數優化指標，并采用正交試驗設計方法，得出環冷機一二段適宜的操作參數組合。結果表明：當其他操作參數不變時，隨著入口風速的增加，出口冷卻空氣所攜帶的焓?呈現先增大后減小的趨勢。環冷機一二段適宜的操作參數為：冷卻空氣進口標況流量8.3×105m3·h-1、料層高度1.6 m和進口風溫424 K，此工況下出口熱載體焓?值比現有實際工況的提高了11.09%。

燒結；傳熱；?；數值模擬；正交試驗

引 言

目前，燒結環冷機的設計與運行主要基于燒結礦的冷卻，而非燒結礦顯熱的回收，因此，現存環冷機操作參數的設置不一定滿足于燒結礦余熱的高效回收。針對此，國內外一些學者利用數值模擬的方法對環冷機中燒結礦的冷卻過程進行了研究。Caputo等[1]簡化建立了環冷機一維穩態模型，提出不同操作參數下氣固穩態仿真模型，用效能傳熱單元數法進行計算。Jang等[2]將4行球體堆積出來的模型當作環冷機固體料層的簡化模型，建立三維湍流模型，對內部換熱及流動過程進行了模擬計算。Prommas等[3]建立實驗平臺，通過多孔介質干燥實驗研究顆粒大小、物料填充方式與進口參數對能量傳遞與?傳遞規律的影響。Hajipour等[4]用數值模擬與解析相結合的方法，研究模型中黏性力項與慣性力項對床層內氣體流動與換熱的影響。Lemos[5]利用非熱力學平衡模型討論湍流流體穿過多孔介質的傳熱傳質現象，認為湍流與固體介質間存在兩種動量傳遞驅動機制。張欣等[6]根據能量守恒定律建立燒結礦氣固換熱一維非穩態數學模型，分析進口風速與臺車速度對環冷機冷卻過程影響。張家元等[7-8]和李茂等[9]結合 Fluent軟件中 UDF、UDS兩項功能，構建了多孔介質非熱力學雙能量方程模型，優化分層布料形式及工藝參數，以提高余熱回收利用率。趙斌等[10]比較了8組環冷機實驗工況，得到了 Nusselt數與孔隙率、Reynolds數的關系，并得到擬合曲線，為環冷機優化提供依據。夏建芳等[11]基于冷卻能耗理論采用控制變量法對單因素進行研究，利用正交法得到環冷機適宜運行參數。Liu 等[12]綜合考慮出口冷卻氣體的熱量與品質，對環冷機操作參數進行優化分析。以上關于環冷機床層內氣固傳熱的研究尚存在不足之處。首先，采用傳統Ergun公式計算料層阻力損失，忽略燒結礦床層阻力損失的特殊性；其次，采用普適經驗公式計算床層內氣固傳熱系數，沒有對床層內氣固傳熱進行針對性分析；最后，以環冷機出口熱載體的?值作為判據，考慮到了回收余熱的品質，但未考慮在余熱回收過程中產生的能耗問題。

根據本課題組對燒結礦床層的已有研究[13-15]，本文以多孔介質模型和局部非熱力學平衡理論為基礎，建立適用于燒結礦冷卻過程的二維穩態氣固交叉錯流傳熱模型。采用多物理場仿真軟件COMSOL對環冷機內的氣固傳熱過程進行數值計算，利用軟件 UDF功能將料層阻力系數與氣固傳熱系數編入模型當中，研究并分析影響環冷機內氣固傳熱的主要影響因素及其影響規律，并在此基礎上，以環冷機一二段出口熱載體所攜帶的焓?作為評價指標，采用正交試驗的方法得出環冷機一二段適宜的熱工參數，該研究將對現行環冷機的運行操作具有指導性意義。

1 操作參數優化判據——出口熱載體焓?

環冷機出口熱載體的熱量不可能全部轉化為功；相同熱量因能級不同也會導致后續發電量的差異；在余熱回收的過程中會產生耗能問題。基于以上3個因素，本文提出將出口熱載體焓?作為環冷機結構與操作參數的優化評價指標[16]。此方法建立在熱力學第一定律與熱力學第二定律基礎上，可以在偏離環境狀態的情況下，更好地分析解釋工質的做功能力，揭示系統內部損失的實質，對于整個系統的熱力學完善具有指導意義。

焓?是溫度?與壓力?之和。式（1）為焓?表達式

溫度?的表達式為

壓力?的表達式為

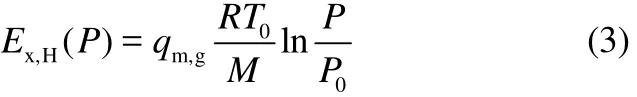
通過環冷機的冷卻氣體，與熾熱的燒結礦換熱后溫度上升，其攜帶的溫度?升高，表現為后續發電；燒結床層可看作多孔介質，氣體經過床層時勢必會產生壓力損失，對焓?值產生負影響，表現為環冷機下部鼓風機的耗電。因此采用焓?來評價出口熱載體的可用性是較為準確和完善的，可以更好地體現環冷機余熱回收的節能效益。

2 模型的建立及驗證

2.1 物理模型

以某企業 360 m2大型燒結機配套環冷機為研究對象。環冷機的冷卻面積為405 m2，沿著臺車運行方向，冷卻段依次分為環冷一段、二段，直至五段，每段長度為24 m。由于環冷機前兩段出口冷卻空氣的溫度較高，具有較高的余熱回收價值，設置集風罩將出口冷卻空氣送入余熱鍋爐系統進行發電，經鍋爐換熱后的冷卻廢氣被循環利用，由環冷機臺車底部進風口鼓入臺車內。由于環冷機的后三段出口冷卻廢氣的溫度較低，余熱回收的價值不高，其主要目的是完成燒結礦的冷卻。因此，本文針對環冷機的一、二段建立物理模型，旨在探索環冷機一、二段的最佳操作參數，以提高環冷機余熱回收系統的噸礦發電量，如圖1所示。

圖1 環冷機余熱回收段示意圖Fig.1 Schematic diagram of period of recovery of waste heat

2.2 基本假設

燒結礦經燒結機燒結，破碎機破碎之后，形成大小不同、形狀不規則的塊狀顆粒。在保證其求解精度的前提下，對環冷機進行簡化處理。目前通常采用的方法是統計平均法[17-18]，經過此方法處理之后，燒結礦冷卻可被看作是多孔介質氣固換熱過程[19]。由此對環冷機的物理模型進行以下簡化處理。

（1）環冷機運行狀況穩定且所有相關設備運行參數恒定；

（2）在穩定狀況下，所有風道口的鼓風量、風速與分壓都是相同的；

（3）燒結礦的體積隨溫度變化熱脹冷縮很小，忽略不計，且顆粒內外溫度一致，沒有溫度梯度；

（4）環冷機的冷卻過程中，輻射傳熱所占比例很小，因此忽略輻射傳熱的影響，只考慮氣體的導熱過程、燒結礦間的導熱過程以及氣體與固體間的對流換熱過程。

2.3 數學模型

利用COMSOL流動模塊中的湍流k-ε應用模式對冷卻氣體流經燒結礦床層過程中的質量守恒及動量守恒進行控制，利用傳熱模塊中的固體傳熱與流體傳熱對燒結礦冷卻過程中的能量守恒進行控制，兩種模塊進行耦合可以對冷卻氣體流經燒結礦的冷卻過程進行傳熱及傳質進行模擬。

（1）連續性方程

（2）動量方程

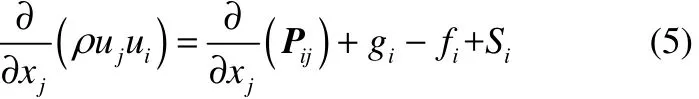
為描述流體在多孔介質內的流動，需要在動量方程中增加一個源項[20]。該源項由兩部分組成，分別為黏性損失項與慣性損失項，分別為式（6）右邊第1項與第2項。

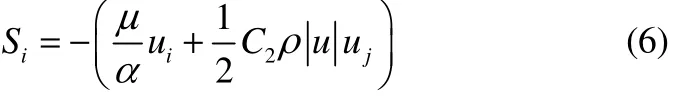
為了確定該源項，需要得出黏性阻力系數和慣性阻力系數，實踐證明，傳統Ergun公式[21]具有很好的普適性，但由于其為半經驗公式，存在一定的誤差，因此本文采用課題組內以燒結礦床層為研究對象得到的修正Ergun公式來來確定黏性阻力系數和慣性阻力系數[22]，分別為

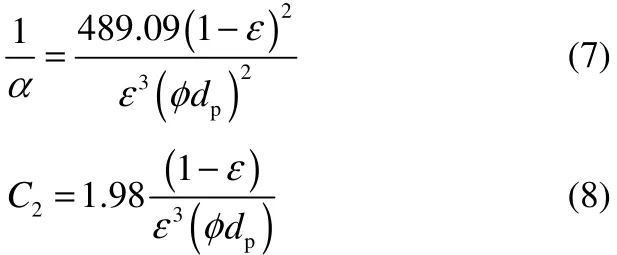
（3）能量方程

采用局部非熱力學平衡雙能量方程來求解多孔介質內的傳熱過程[23-26]。

固相

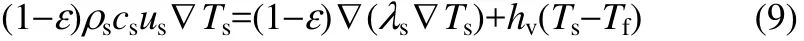
氣相

hv可由Achenbach 準則關系式[27]確定

此處h的確定摒棄前人常用的經驗Nu公式，采用本課題組針對燒結礦床層中氣固傳熱系數的研究結果，得到h由式（12）確定[28]

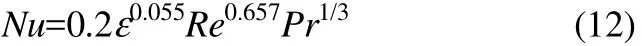
在模擬過程中，余熱回收的量利用空氣顯熱量Q來表示。回收氣體熱量Q采用式(13)進行計算[29]

2.4 邊界條件

以環冷機的工作原理作為基礎，模型分為以下幾個邊界：冷卻氣體入口，冷卻氣體出口，燒結礦入口，燒結礦出口。計算區域的氣體入口采用速度邊界條件，根據實際情況確定入口速度，進入余熱回收區的冷卻氣體是來自余熱鍋爐的循環氣體，溫度為404 K；氣體出口采用壓力出口邊界條件，相對壓強大小根據實際測試給出，環冷機入口處采用溫度邊界條件，賦予燒結礦進入環冷機的初始溫度。

2.5 模型計算結果驗證

結合實際現場的生產，對應環冷機模型的標況條件下，通過測試現場環冷機余熱利用區出口氣體溫度來驗證模型的可靠性。將環冷機余熱回收區平均分成8段，除起點外共設立8個測點；出口空氣的溫度利用熱電偶來進行測量。每個測點在臺車的上平面上設置3個測量點，每個位置測3次，取平均值[30]。

由圖2可知環冷機余熱回收區出口空氣溫度的模擬結果，結果平均誤差為3.7%，與實際測量結果相比最大誤差小于 8%，模擬所得環冷機進口端與出口端燒結礦溫度與實際情況也基本相符，因此認為本文所建立的模型以及計算結果是可靠的。

圖2 出口氣體實測平均溫度與仿真結果對比Fig.2 Comparison of measured and simulated outlet air average temperatures

3 模擬結果與分析

模擬計算以某鋼廠年產量 3.9×106t燒結機的配套405 m2環冷機作為基準工況[31]，經現場測定得到各項參數，其具體數值如表1所示。

通過改變體積流量（進口風速）、料層高度和余熱利用區的進口風溫，研究單一參數對環冷機冷卻過程的影響。

3.1 進口風速的影響

出口氣體溫度及熱量隨進口風速變化如圖3所示。當進口風速由1.923 m·s-1增加至3 m·s-1時，出口氣體的體積流量不斷增加，出口空氣的平均溫度不斷降低，由637.6 K下降至572.0 K。雖然溫度降低，但由于其流量增大，單位時間內出口氣體所攜帶的顯熱量不斷增加。由于燒結礦溫度不斷降低，氣體與其進行熱交換的難度提升，由圖3可以看出出口氣體熱量增加速率逐漸減緩。

表1 環冷機標況參數Table 1 Standard condition of sinter annular cooler

圖3 出口氣體溫度及熱量隨進口風速變化曲線Fig.3 Temperature and heat quantity of outlet air vary with inlet air speeds

出口氣體焓?、溫度?及壓力?隨進口風速變化如圖4所示。由圖4可知隨著進口風速的增加，出口氣體的焓?不斷增大，但是增加的速度不斷減緩，在達到峰值之后開始逐漸回落。這是由于出口氣體的焓?中，溫度?占主導作用，且溫度?受熱量與能級兩個因素影響。隨著進口風速增加，空氣與燒結礦換熱充分，出口氣體攜帶的熱量不斷增加，但是由于溫度降低，能級不斷減小。在溫度?達到頂峰前，熱量的增加占主導地位，表現為溫度?上升。但逐漸能級的下降起主導作用，表現為溫度?下降。同時由于壓力?的存在，使得溫度?的拐點提前。由此在考慮焓?的情況下，確定標準工況最佳進口風速為2.3 m·s-1。

圖4 出口氣體焓?、溫度?及壓力?隨進口風速變化曲線Fig.4 Enthalpy exergy, temperature exergy and pressure exergy of outlet air vary with inlet air speeds

3.2 料層高度的影響

由于集風罩和風箱之間距離的限制，環冷機臺車的壁面高度只能達到 1.6 m，所以探究料層高度不宜超過該值。環冷機作為燒結機的附屬裝置，在改變環冷機中燒結礦的料層高度時，為了不改變燒結機的產量，環冷機臺車的前進速度也需要進行相應改變。現行工況料層高度為 1.4 m，臺車的前行速度為0.022 m·s-1；以1.2、1.3、1.5、1.6 m料層高度作為研究對象時，對應的臺車前進速度分別為0.0259、0.0239、0.0207、0.0194 m·s-1。

出口氣體溫度及熱量隨料層高度變化如圖5所示。隨著料層高度的增加，氣體穿過料層的時間增加，意味著與燒結礦的換熱時間增長，出口氣體的平均溫度不斷升高，由627.98 K上升至642.15 K。出口氣體攜帶的熱量也不斷增加，由 233.3×106kJ·h-1提高至 251.2×106kJ·h-1。

圖5 出口氣體溫度及熱量隨料層高度變化曲線Fig.5 Temperature and heat quantity of outlet air vary with height of sinter

出口氣體焓?、溫度?及壓力?隨料層高度變化如圖6所示。由圖6可知，隨著料層高度的增加，出口氣體所攜帶的溫度?不斷增加，空氣經過料層產生的阻力損失也隨之增加，壓力?不斷減小，但由于溫度?增加占主導影響，出口空氣的焓?不斷增加。在生產條件允許條件下盡量提高料層高度，有利于余熱的回收利用。

圖6 出口氣體焓?、溫度?及壓力?隨料層高度變化曲線Fig.6 Enthalpy exergy, temperature exergy and pressure exergy of outlet air vary with sinter heights

3.3 進口風溫的影響

余熱利用區的進口空氣來自于余熱鍋爐，標準工況下來自余熱鍋爐的廢氣溫度為404 K，為不影響余熱鍋爐的正常生產，在與企業技術人員進行交流研究后，將溫度允許波動范圍限制在±20 K以內。

出口氣體溫度及熱量隨進口風溫變化如圖7所示。隨著進口風溫的不斷增加，出口空氣的平均溫度不斷上升，由627 K上升至657 K。由于進口風溫的增加，氣體與燒結礦之間的溫差減小，傳熱條件惡化，從而導致出口氣體熱量不斷提高，但上升趨勢逐漸減緩。

圖7 出口氣體溫度及熱量隨進口風溫變化曲線Fig.7 Temperature and heat quantity of outlet air vary with temperatures of inlet air

出口氣體焓?、溫?及壓力?隨進口風溫變化如圖8所示。由于溫度的提高，能級也在不斷提高，出口熱載體具有的做功能力增強。與此同時，由于進口空氣溫度提高，相應的物性參數發生改變，氣流穿過料層的阻力損失降低，因此焓?值處于平穩上升的態勢。

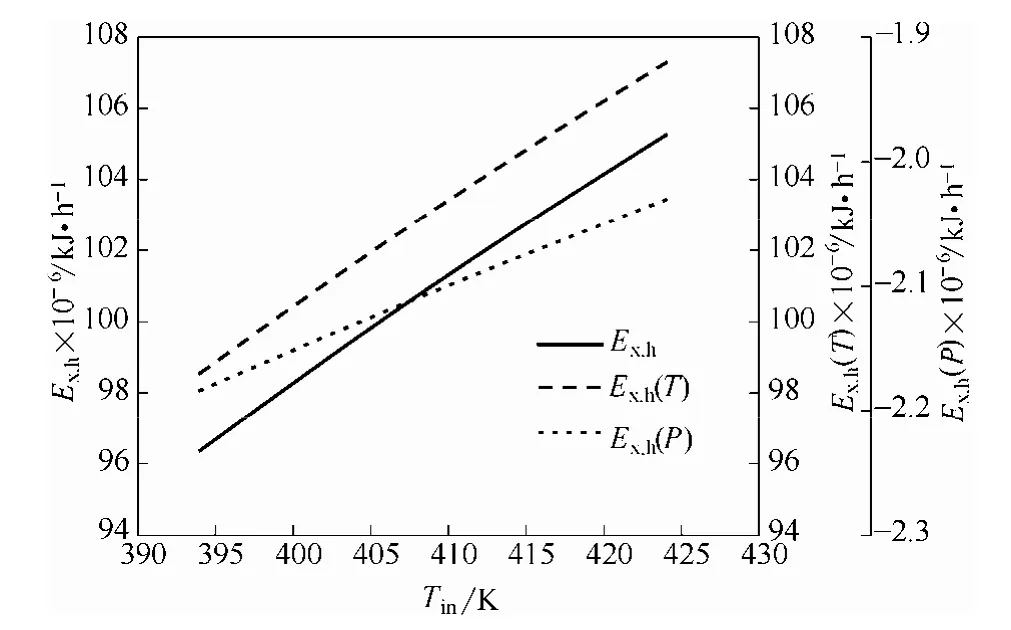
圖8 出口氣體焓?、溫度?及壓力?隨進口風溫變化曲線Fig.8 Enthalpy exergy, temperature exergy and pressure exergy of outlet air vary with inlet air temperatures

4 正交試驗仿真及優化

利用正交試驗法對空氣進口風速、料層高度和進口空氣溫度3個參數進行優化分析。進口風速取標況下最佳風速附近的4個水平，分別為2.1、2.2、2.3和2.4 m·s-1；料層高度與進口風速在工況限制條件下也分別取4個水平。表2列出了該正交試驗的因素與水平。

表2 正交試驗的因素與水平Table 2 Factors and levels of orthogonal experiments

選擇正交表L16（4 3）進行試驗分析，即3參數、4水平和16工況的正交試驗，試驗優化目標為環冷機余熱回收段出口熱載體的焓?，仿真結果如表3所示。

表4中Ⅰi表示參數i在1水平工況下的平均值；以此類推。由結果可知Ⅱ1>Ⅲ1>Ⅳ1>Ⅰ1，說明參數1即空氣進口風速在2.2 m·s-1時為最優水平；Ⅳ2>Ⅲ2>Ⅱ2>Ⅰ2，說明參數2即料層高度在1.6 m時為最優水平；Ⅳ3>Ⅲ3>Ⅱ3>Ⅰ3，說明參數3即進口氣體風溫在424 K時為最優水平。

表3 正交試驗結果Table 3 Orthogonal experimental results

表4 不同水平下各參數的平均值Table 4 Comprehensive value of parameters under different levels/kJ·h-1

Ri表示參數i的最優水平與最差水平之差，反映了該參數對結果的影響程度，差值越大表示影響程度越大。由表可知R3>R2>R1，因此參數3即進口空氣溫度對結果影響最大，參數2料層高度次之，參數1空氣進口速度對結果影響最小。由表4可知最優組合為進口風速2.2 m·s-1，料層高度1.6 m，進口空氣溫度424 K，此時出口氣體的焓?值最大為110.59×106kJ·h-1。

5 結 論

（1）著眼于環冷機-余熱鍋爐的能量回收利用環節，提出了環冷機結構與操作參數的優化判據——出口熱載體（即冷卻燒結礦的氣體）焓?。

（2）在環冷機標準工況基礎下，基于生產實際的可調性，進口風速在1.923～3 m·s-1范圍內，隨著入口風速的不斷增加，出口熱載體所攜帶的焓?呈現先增大后減小的趨勢，在風速為2.3 m·s-1時達到峰值；進口風溫在394～424 K范圍內，隨著溫度的增加出口熱載體的焓?逐漸增加，增加態勢平穩；料層高度在1.2～1.6 m范圍內，隨著料層高度的增加，出口熱載體所攜帶的焓?逐漸增加，增加的速率逐漸減小。

（3）以焓?作為評判指標，通過正交試驗法對影響環冷機冷卻過程的3個參數進行優化分析，得出以下結論：對于國內某405 m2環冷機而言，考慮其操作性與可接受性，較為理想的運行參數為：料層高度1.6 m，比現有增加14.3%，每臺鼓風機冷卻風量4.35×105m3·h-1，比現有增加14.4%；進口風溫提升至 424 K；則出口熱載體的焓?將由99.55×106kJ·h-1提升至 110.59×106kJ·h-1，提升了11.09%。假設噸礦發電量與出口熱載體焓?值正相關，則噸礦發電量將提高相應程度，達到我國燒結余熱發電先進水平。

符 號 說 明

cg,in,cg,out——分別為進口氣體與出口氣體比熱容，J·kg-1·K-1

cp——工質的比定壓熱容，kJ·kg-1·K-1

cs,cf——分別為燒結礦和空氣比熱容，J·kg-1·K-1

fi——作用在單位體積流體反方向上的阻力

gi——作用在單位體積流體i方向上的體積力

hv——氣固之間體積對流傳熱系數，W·m-3·K-1

M——氣體摩爾質量，kg·mol-1

P,P0——分別為工質壓力損失與環境壓力，Pa

Pij——表面力矢量，包括靜壓力與流體黏性壓力，Pa

Q——出口氣體熱量，kJ

qm,g——氣體質量流量，kg·h-1

R——理想氣體常數，8.3145 J·mol-1·K-1

Tin,Tout——分別為臺車下部進口氣體和上部出口氣體溫

度，K

Ts,Tf——分別為固體和氣體溫度，K

T0——環境溫度，K

us,uf——分別為燒結顆粒平移速度和氣體表觀流速，

m·s-1

λs,λf——分別為燒結礦和空氣熱導率，W·m-1·K-1

ρs,ρf——分別為燒結礦和空氣密度，kg·m-3

下角標

f ——氣體

s ——固體

[1] CAPUTO A C, CARDARELLI G, PELAGAGGE P M. Analysis of heat recovery in gas-solid moving beds using a simulation approach[J]. Applied Thermal Engineering, 1996, 16(16): 89-99.

[2] JANG J Y, CHIU Y W. 3-D Transient conjugated heat transfer and fluid flow analysis for the cooling process of sintered bed[J]. Applied Thermal Engineering, 2009, 29(14/15): 2895-2903.

[3] PROMMAS R, KEANGIN P, RATTANADECHO P. Energy and exergy analyses in convective drying process of multi-layered porous packed bed ☆[J]. International Communications in Heat & Mass Transfer, 2010, 37(8): 1106-1114.

[4] HAJIPOUR M, DEHKORDI A M. Transient behavior of fluid flow and heat transfer in vertical channels partially filled with porous medium: effects of inertial term and viscous dissipation[J]. Energy Conversion & Management, 2012, 61(5): 1-7.

[5] LEMOS M J S D. Analysis of turbulent double-diffusive free convection in porous media using the two-energy equation model[J].International Communications in Heat & Mass Transfer, 2014, 52(2):132-139.

[6] 張欣, 溫治, 樓國鋒, 等. 高溫燒結礦氣-固換熱過程數值模擬及參數分析[J]. 北京科技大學學報, 2011, 33(3): 339-345.ZHANG X, WEN Z, LOU G F,et al. Numerical simulation and Parameters analysis on the gas-solid heat transfer process of height temperature sinter[J]. Journal of University of Science and Technology Beijing, 2011, 33(3): 339-345.

[7] ZHANG X, CHEN Z, ZHANG J,et al. Simulation and optimization of waste heat recovery in sinter cooling process[J]. Applied Thermal Engineering, 2013, 54(1): 7-15.

[8] 張家元, 田萬一, 戴傳德, 等. 環冷機分層布料仿真與優化[J]. 化工學報, 2012, 63(5): 1385-1390.ZHANG J Y, TIAN W Y, DAI C D,et al. Simulation and optimization of sinter annular cooler layer-loading[J]. CIESC Journal, 2012, 63(5):1385-1390.

[9] 李茂, 母玉同, 張家元, 等. 燒結環冷機分層布料的數值模擬與優化[J]. 中南大學學報(自然科學版), 2013, 44(3): 1228-1234.LI M, MU Y T, ZHANG J Y,et al. Numerical simulation and optimization of sinter cooler in multilayered burden distribution[J].Journal of Central South University(Science and Technology), 2013,44(3): 1228-1234.

[10] 趙斌, 趙利杰, 屈婷婷, 等. 環冷機內燒結礦通道氣固傳熱實驗關聯式[J]. 熱科學與技術, 2013, 12(4): 302-306.ZHAO B, ZHAO L J, QU T T,et al. Experimental correlation of gas-solid heat transfer for sinter channel in circular cooler[J]. Journal of Thermal Science and Technology, 2013, 12(4): 302-306.

[11] 夏建芳, 喻向陽, 趙先瓊. 基于環冷機冷卻能耗最小目標的工藝參數優化[J]. 鋼鐵研究學報, 2016, 28(1): 13-19 XIA J F, YU X Y, ZHAO X Q. Optimization of process parameters based on minimum target of cooling energy consumption of sinter cooler[J]. Journal of Iron and Steel Research, 2016, 28(1): 13-19.

[12] LIU Y, YANG J, WANG J,et al. Energy and exergy analysis for waste heat cascade utilization in sinter cooling bed[J]. Energy, 2014, 67(4):370-380.

[13] 董輝, 趙勇, 蔡九菊, 等. 燒結-冷卻系統的漏風問題[J]. 鋼鐵,2012, 47(1): 95-99.DONG H, ZHAO Y, CAI J J,et al. Leakage of sintering-cooling system[J]. Iron and Steel, 2012, 47(1): 95-99.

[14] 孫用軍, 董輝, 馮軍勝, 等. 燒結-冷卻-余熱回收系統熱力學分析[J]. 鋼鐵研究學報, 2015, 27(1): 16-21.XUN Y J, DONG H, FENG J S,et al. Thermodynamic analysis of waster heat recovery for sinter-cooling system[J]. Journal of Iron and Steel Research, 2015, 27(1): 16-21.

[15] FENG J, DONG H, DONG H. Modification of Ergun’s correlation in vertical tank for sinter waste heat recovery[J]. Powder Technology,2015, 280(1): 89-93

[16] 傅秦生. 能量系統的熱力學分析方法[M]. 西安: 西安交通大學出版社, 2005: 98-107.FU Q S. Thermodynamic Analysis Method of Energy System[M].Xi`an: Xi'an Jiaotong University Press, 2005: 98-107.

[17] PELAGAGGE P M, CAPUTO A C, CARDARELLI G. Optimization criteria of heat recovery from solid beds[J]. Applied Thermal Engineering, 1997, 17(1): 57-64.

[18] PELAGAGGE P M, CAPUTO A C, CARDARELLI G. Comparing heat recovery schemes in solid bed cooling[J]. Applied Thermal Engineering, 1997, 17(11): 1045-1054

[19] HINKLEY J, WATERS A G, LITSTER J D. An investigation of pre-ignition[J]. International Journal of Mineral Processing, 1994,42(1/2): 37-52.

[20] 劉偉, 范愛武, 黃曉明. 多孔介質傳熱傳質理論與應用[M]. 北京:科學出版社, 2006: 28-32.LIU W, FAN A W, HUANG X M. Porous Media Theory and Application of Heat and Mass Transfer[M]. Beijing: Science Press,2006: 28-32.

[21] JIK C, LEONG, KAI W,et al. Effect of sinter layer porosity distribution on flow and temperature fields in a sinter cooler[J].International Journal of Minerals, Metallurgy and Materials, 2009,16(3): 265-272.

[22] 馮軍勝, 董輝, 李明明, 等. 燒結余熱回收豎罐內固定床層的阻力特性[J]. 中南大學學報(自然科學版), 2014, 45(8): 2566-2571.FENG J S, DONG H, LI M M,et al. Resistance characteristics of fixed bed layer in vertical tank for recovering sinter waste heat[J].Journal of Central South University(Science and Technology), 2014,45(8): 2566-2571.

[23] FENG J, DONG H, GAO J Y,et al. Numerical investigation of gas-solid heat transfer process in vertical tank for sinter waste heat recovery[J]. Applied Thermal Engineering, 2016, 107(25): 135-143.

[24] 李菊香, 涂善東. 考慮局部非熱平衡的流體層流橫掠多孔介質中恒熱流平板的傳熱分析[J]. 化工學報, 2010, 61(1): 10-14.LI J X, TU S D. Heat transfer of laminar flow over a plate embedded in porous medium with a constant heat flux under local non-equilibrium condition[J]. CIESC Journal, 2010, 61(1): 10-14.

[25] 陶斌斌, 楊歷, 劉春元. 多孔介質干燥的非平衡熱力學模型[J]. 河北工業大學學報, 2005, 34(1): 109-112.TAO B B, YANG L, LIU C Y. Porous media`s drying model of non-equilibrium thermodynamics[J]. Journal of Hebei University of Technology, 2005, 34(1): 109-112.

[26] PRAT M. Recent advances in pore-scale models for drying of porous media[J]. Chemical Engineering Journal, 2002, 86(1/2): 153-164.

[27] KYE S H, JAE H J, WON K L. Fixed-bed adsorption for bulk component system: non-equilibrium non-isothermal and non-adiabatic model[J]. Chemical Engineering Science, 1995, 50(5):813-825.

[28] 馮軍勝, 董輝, 劉靖宇, 等. 燒結礦余熱回收豎罐內氣固傳熱特性[J]. 化工學報, 2015, 66(11): 4418-4423.FENG J S, DONG H, LIU J Y,et al. Gas-solid heat transfer characteristics in vertical tank for sinter waster heat recovery[J].CIESC Journal, 2015, 66(11): 4418-4423.

[29] BISIO G. First- and second-law analyses of energy recoveries in blast-furnace regenerators[J]. Energy, 1996,21(2): 147-155.

[30] 張小輝, 張家元, 戴傳德, 等. 燒結礦冷卻過程數值仿真與優化[J].化工學報, 2011, 62(11): 3081-3087.ZHANG X H, ZHANG J Y, DAI C D,et al. Optimization and simulation of sinter cooling process[J]. CIESC Journal, 2011, 62(11):3081-3087.

[31] 常弘. 環冷機內氣固傳熱過程數值計算及其應用[D]. 沈陽: 東北大學, 2016.CHANG H. Numerical calculation of gas-solid heat transfer in a sinter cooler and its application[D]. Shenyang: Northeastern University, 2016.

date:2017-04-17.

Prof. DONG Hui, dong@mail.neu.ecu.cn

supported by the Science and Technology Project of Liaoning Province(2015307001).

Simulation and optimization of thermal parameter of sinter annular cooler based on enthalpy exergy of heat carrier

ZHANG Sheng, FENG Junsheng, DONG Hui
(SEP Key Laboratory of Eco-industry,Northeastern University,Shenyang110819,Liaoning,China)

With a 405 m2annular sinter cooler as research objects, the two-dimensional steady-state numerical model of annular sinter cooler was established on the basis of the porous media and local non-equilibrium thermodynamics theory. The moving speed along with the moving direction of sinter trolley was defined into the numerical model with the help of user-defined functions in COMSOL. The main factors influencing the sinter waste heat recovery and influence laws were analyzed. The enthalpy exergy of outlet cooling air of annular sinter cooler was taken as the evaluation index of parameter optimization, and the suitable operating parameters combination of first and second stages in annular sinter cooler were obtained through the method of orthogonal experiment. The results show that when the other operating parameters are constant, the enthalpy exergy of outlet cooling air first increases and then decreases with the increase of inlet air velocity. The suitable operating parameters are as follows. The standard flow of inlet cooling air is 8.3×105m3·h-1. The height of sinter bed layer is 1.6 m and the temperature of inlet cooling air is 424 K. Under this condition, the exergy of outlet heat carrier increases by 11.09% than existing working condition.

sintering; heat transfer; exergy; numerical simulation; orthogonal experiment

TF 046.4；TK 11+5

A

0438—1157（2017）11—4129—08

10.11949/j.issn.0438-1157.20170406

2017-04-17收到初稿，2017-08-02收到修改稿。

聯系人：董輝。

張晟（1993—），男，碩士研究生。

遼寧省科技計劃項目（2015307001）。