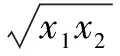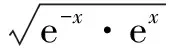函數極值點偏移的判定和應用
尹愛國
(湖南省長沙市明德中學,湖南 長沙 410000)
函數極值點偏移的判定和應用
尹愛國
(湖南省長沙市明德中學,湖南 長沙 410000)
綜述函數的極值條件,結合極值點偏移的性質,提出極值點偏移的判定方法.
函數極值點;判定方法;應用
問題引入:(2016·全國卷Ⅰ·理21)已知函數f(x)=(x-2)ex+a(x-1)2有兩個零點.
(Ⅰ)求實數a范圍;
(Ⅱ)設x1、x2是f(x)的兩個零點,證明:x1+x2<2
解析(Ⅰ)答案:a>0.
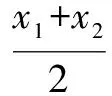
筆者在多年的教學中發現類似問題在高考壓軸題中頻頻出現,因此對此類問題進行了研究,找出了解決此類問題的一種通法,供大家參考.
一、極值點偏移的判定方法.
設已知函數y=f(x),在區間x∈D上滿足:x=a是函數的唯一極值點,x1,x2∈D,x1≠x2,f(x1)=f(x2)
第一步:判斷曲線在D上的開口方向.
類似于拋物線,若曲線f(x)在D上存在唯一極值點,則曲線在D上存在開口方向問題.若x=a為y=f(x)的極小值點,則f(x)在D上的開口向上;若x=a是曲線y=f(x)的極大值點,則y=f(x)在D上的開口向下.
第二步:構造函數F(x)=f(x)-f(2a-x)或F(x)=f(a-x)-f(a+x).運用導數判定x 下面結合上述步驟解決文首提出問題的第二問. (Ⅱ)解由(Ⅰ)有:a>0,x=1為y=f(x)的唯一極值點,且為極小值點,函數定義域為R,∴f(x)的圖象在R上開口向上.構造函數F(x)=f(x)-f(2-x)=xe2-x+(x-2)ex. 求得F′(x)=(x-1)(ex-e2-x).x=1時,F′(x)=0,x≠1時,F′(x)>0,∴F(x)R上遞增. 又F(1)=0,∴x<1時,F(x) 例(2014·江蘇南通二模·20題)設函數f(x)=ex-ax+a(a∈R),其圖象與x軸交于點A(x1,0),B(x2,0)(x1 (Ⅰ)求a的取值范圍; 解析(Ⅰ)定義域為x∈R,f′(x)=ex-a. 當a≤0時,f′(x)>0,f(x)在R上遞增,函數不可能有兩個極值點.當a>0時,∵當x∈(-∞,lna)時,f′(x)<0,x∈(lna,+∞)時,f′(x)>0. ∴f(x)在(-∞,lna)上單調遞減,在(lna,+∞)上單調遞增. ∴當x=lna時,f(x)min=f(lna)=elna-alna+a=2a-alna. ∵f(x)的圖象與x軸有兩交點, ∴f(x)min=2a-alna<0, ∴a>e2. (Ⅱ)證明:由(Ⅰ)知:a>e2,x=lna為y=f(x)的唯一極值點,且為極小值點. ∴f(x)的圖象開口向上. ∴x1 ∴F(x)在(0,+∞)上單調遞減,∴F(x) [1]華東師范大學數學系.數學分析[M].北京:高等教育出版社,1991. [2]譚琨.多元函數極值的研究與應用[J].安慶師范學院學報,2005. [責任編輯:楊惠民] 2017-07-01 尹愛國,男,中學一級教師,碩士,長沙市骨干教師,從事高中數學教學研究. G632 A 1008-0333(2017)28-0027-02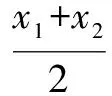
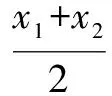
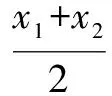

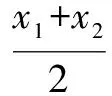
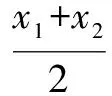
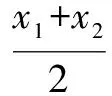
二、極值點偏移的性質
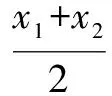
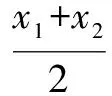
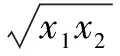
三、例題展示