導(dǎo)數(shù)，物理解題的一把利器

馮云周

(河北隆堯第一中學(xué)，河北 邢臺 055350)

導(dǎo)數(shù)，物理解題的一把利器

馮云周

(河北隆堯第一中學(xué)，河北 邢臺 055350)

運用數(shù)學(xué)知識處理物理問題是當今高考對學(xué)生的能力考查之一，而導(dǎo)數(shù)又是現(xiàn)行高中數(shù)學(xué)教材中的一項新增內(nèi)容，因此，如何把導(dǎo)數(shù)知識很好地運用到高中物理解題的實際中去，已經(jīng)成為了很多人正在積極探索和研究的一項新課題.本文在這方面做出了一些初步的嘗試.

導(dǎo)數(shù)；高中物理；解題

現(xiàn)行的高中數(shù)學(xué)課本中新增了對導(dǎo)數(shù)等內(nèi)容的學(xué)習(xí)，為中學(xué)生應(yīng)用高等數(shù)學(xué)知識來解決問題奠定了知識基礎(chǔ).實際上，許多高中物理題如果用導(dǎo)數(shù)來分析和求解，就會顯得思路簡捷，便于理解和接受，解題效果也會不同凡響.下面是我在平時的教學(xué)實踐中，嘗試運用導(dǎo)數(shù)來解中學(xué)物理題的一些初步的探索和體驗，現(xiàn)分享給大家，希望能給您帶來一些啟迪！

一、巧用導(dǎo)數(shù)，豁然開朗

題1 一物體沿x軸做簡諧運動，振幅為8cm，頻率為0.5Hz，在t=0時位移是4cm，且向x軸負方向運動，試寫出用正弦函數(shù)表示的振動方程.

這是最近我的學(xué)生們所做的一道練習(xí)題，所附解答如下：

設(shè)簡諧運動的表達式為：x=Asin(ωt+φ)

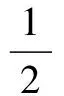
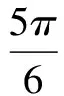
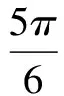
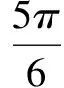
冥思苦想了一會兒，我忽然靈光一閃：“物體向x軸負方向運動”，說明此時速度為負，而位移對時間的一階導(dǎo)數(shù)不正是速度嗎！于是我得出了下面的解釋：

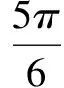
如此稍加點撥，是否有豁然開朗的感覺呢？

二、耳目一新，教學(xué)相長

題2 如圖1所示，為一單擺的共振曲線，該單擺的擺長約為多少？共振時單擺的振幅是多大？共振時擺球的最大速度和最大加速度各為多少？(g取10 m/s2)

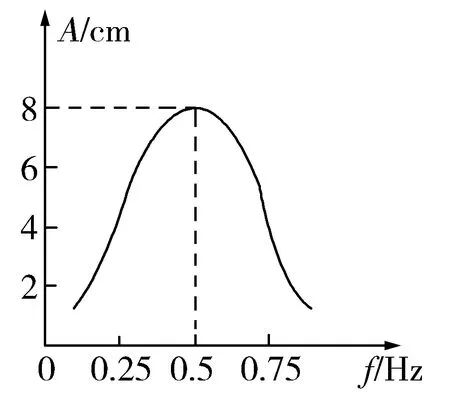
圖1

這是在學(xué)習(xí)共振時我給學(xué)生們講解的一道例題，這道題的重點和難點在最后一問，一般解法如下：

從共振曲線可知，單擺發(fā)生共振時，振幅A=8cm.設(shè)單擺的最大偏角為θ，擺球所能達到的最大高度為h，由機械能守恒定律得：

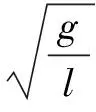
擺球在最大位移處加速度最大，有mgsinθ=mam

那么，這道題有沒有其他更好的解法呢？當我在辦公室里深入思考的時候，一向?qū)W習(xí)認真、善于思考的張同學(xué)輕聲打報告走了進來，向我展示了他的做法.整理如下：

單擺共振時做簡諧運動，若從平衡位置開始計時，則振動的位移x=0.08sin(2πft)=0.08sinπt，振動的速度v=x′(t)=0.08πcosπt，可見速度的最大值vm=0.08π=0.25 m/s；

振動的加速度a=v′(t)=-0.08π2sinπt，可見加速度的最大值am=0.08π2=0.80 m/s2.

這種解法怎樣？是否有耳目一新的感覺呢？所謂“教學(xué)相長”，我們這些當老師的是不是也應(yīng)該感謝我們的學(xué)生呢？

三、腦洞大開，躍躍欲試

位移x對時間t求導(dǎo)是速度

速度v對時間t求導(dǎo)是加速度

由此想開去——

功W對時間t求導(dǎo)是什么？是功率P！

功W對位移x求導(dǎo)又是什么？是力F！

還有——

動量的變化△p對時間t求導(dǎo)等于合力F

角度θ對時間t求導(dǎo)等于角速度ω

電荷量q對時間t求導(dǎo)等于電流I

磁通量Φ對時間t求導(dǎo)等于感應(yīng)電動勢E

繼續(xù)——

電勢φ對距離d求導(dǎo)等于電勢差U

電勢差U對距離d求導(dǎo)等于場強E

勢能Ep對距離r求導(dǎo)等于相應(yīng)的保守力F

……

總之，只要一個物理量是相對于另一個物理量的變化率，那么這個物理量就可以運用導(dǎo)數(shù)來分析求解.

怎么樣？腦洞大開了吧！是否有種躍躍欲試的沖動呢？那好，心動不如行動！下面再做兩題：

題3 如圖2所示，矩形線圈匝數(shù)為n，在勻強磁場中繞OO＇軸轉(zhuǎn)動，設(shè)線圈的兩個邊長分別是L1和L2，轉(zhuǎn)動時角速度是ω，在磁場的磁感應(yīng)強度為B.

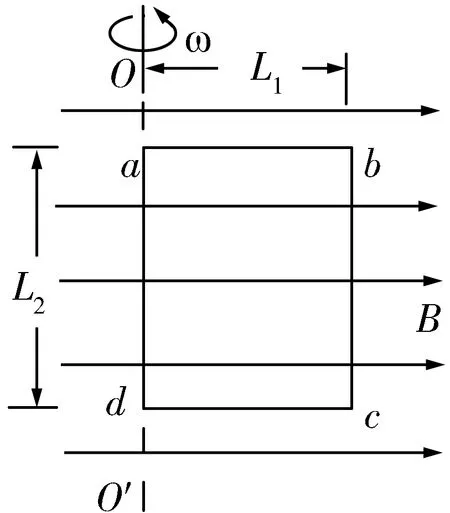
圖2

試證明：在圖示位置時，線圈中的感應(yīng)電動勢為E=nBSω，其中S=L1L2，為線圈面積.

本題一般做法如下：

線圈繞OO＇軸轉(zhuǎn)動，線圈中長為L2的邊都在切割磁感線，根據(jù)公式E=Blvsinθ可得：E=nBL2vsinθ，而圖示位置θ=90°，切割速度為v=ωL1，代入可得：E=nBSω，其中S=L1L2，為線圈面積.

下面再用求導(dǎo)的方法來做：

當線圈在磁場中轉(zhuǎn)動時，若從圖示位置開始計時，則穿過線圈平面的磁通量瞬時值表達式為：φ(t)=Φmsinωt=BL1L2sinωt

每匝線圈中產(chǎn)生的感應(yīng)電動勢e0(t)=φ′(t)=BL1L2ωcosωt

故n匝線圈中產(chǎn)生的總的感應(yīng)電動勢e(t)=nBL1L2ωcosωt

圖示位置t=0，E=nBSω，其中S=L1L2，為線圈面積.證畢.

兩種方法相比，你不覺得用求導(dǎo)的方法顯得更加簡捷而暢快嗎？

[1]張維善.普通高中課程標準實驗教科書物理選修3-2[M].北京：人民教育出版社，2010(4):18.

[2]任滿紅翰元設(shè)計系列.高二物理.四[M].北京：現(xiàn)代教育出版社，2016(6):15.

[責任編輯：閆久毅]

2017-07-01

馮云周，1970年2月，男，河北隆堯，河北隆堯一中 ，中學(xué)高級，本科，物理教育.

G632

A

1008-0333(2017)28-0050-02