基于Smith-PID的數字PCR檢測儀液路雙閉環比值控制系統的設計

陳慶明,劉經龍,李冬梅

廣東順德工業設計研究院(廣東順德創新設計研究院)a.精密儀器部;b.電子信息部,廣東 佛山 528311

基于Smith-PID的數字PCR檢測儀液路雙閉環比值控制系統的設計

陳慶明a,劉經龍b,李冬梅a

廣東順德工業設計研究院(廣東順德創新設計研究院)a.精密儀器部;b.電子信息部,廣東 佛山 528311

液路系統輸出液體的精度、速度、穩定性是數字PCR檢測儀實現功能的基礎.針對基于微流控芯片的數字PCR檢測儀中液路系統出現的大阻力、大滯后的問題,本文提出基于Smith-PID算法的雙閉環控制系統的液路結構.根據注射泵、控制對象的數學模型以及Smith預估控制器原理,構建雙閉環比值控制系統,并利用Simulink對于系統進行建模和仿真,得到相比于傳統PID較好的系統的響應曲線.在數字PCR檢測儀的液路系統驗證中,對比響應曲線發現,與傳統PID控制的雙閉環液路相比,Smith-PID控制的雙閉環比值控制系統的樣品調節時間減少2/3,稀釋液調節時間減少1/3,穩態誤差減少8%,提高了系統流量輸出的穩定性、準確性、快速性.

數字PCR;Smith-PID控制;雙閉環比值控制;液路系統

引言

液滴式數字PCR主要分成液滴生成、PCR擴增、熒光檢測3個部分,數字PCR檢測儀是的熒光信號檢測分析部分.液路系統作為數字PCR檢測儀的重要部分,將含有熒光染色的DNA片段的液滴,與作為稀釋液的油,按照一定關系注入檢測的微流控芯片,利用微流控芯片的結構以及液滴和稀釋油關系,使得液滴按依次單個通過微流控芯片的檢測段[1-2].控制液滴和稀釋油的流速是保證液滴完整、保證液滴單個通過微流控芯片的前提,也是后續信號檢測的保證,是整個基于微流控芯片的數字PCR檢測儀的核心技術之一[3-4].

傳統的液流系統主要采用傳統的PID控制器或者模糊PID控制方法,此方法在較大的通道、阻力較小、滯后效應不嚴重的液流系統是有效的[5-6].但是,在醫療設備的小體積、少樣品、精密化的過程中,微流控芯片技術作為創新有效的技術引入到醫療器械中.微流控芯片的結構和流道相比于傳統的流道小得多,管道尺寸在毫米量級,因此,微流控芯片的阻力比起傳統的管路阻力要大得多,傳統液路出現的問題以及解決的方法,并不完全適用于基于微流控芯片檢測的液路系統[7-8].

數字PCR檢測儀是基于微流控芯片研制的醫療檢測設備,其中的液流系統是大阻力、大滯后的非線性系統,并且作為動力源的注射泵輸出存在脈動,對液流系統控制流量存在干擾,反饋調節參數滯后,特別在阻力很大的微流控液路系統中,實時精確控制液滴和稀釋液的流速存在困難[9-12].

為解決以上問題,本文研究將Smith-PID控制器與液路系統的結構相結合,建立Smith-PID雙閉環比值控制系統,建立基于Smith-PID的雙閉環比值控制系統仿真模型,結果顯示該控制對于液滴樣本和稀釋液兩者的流速控制有很好的準確性,增強液滴樣本和稀釋油之間的聯系,減輕原系統的嚴重滯后現象.

1 數字PCR檢測儀液路雙閉環控制系統結構

數字PCR檢測儀液路系統的流量流速的設定由控制界面輸入,經過控制器的處理,控制信號經過驅動器驅動注射泵的步進電機,通過控制信號的變化達到流體流量速度的目的.又經過流量傳感器,將反饋值與設定值比較,實時調節,實現輸出的流量速度控制在目標穩定值.簡化液路系統模型,進行建模,單液路控制原理,見圖1.

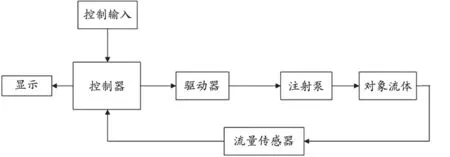
圖1 液路系統單回路控制原理圖

為克服液流的滯后問題,實現液路系統輸出的流量速度的精確控制和解決樣本液滴與稀釋油之間的相關性問題,使用流量傳感器的流量反饋,在系統中建立起樣本和稀釋液的各自的閉環控制以及樣本與稀釋液之間的比值控制,其中,控制算法采用Smith-PID算法,雙閉環比值控制的結構,見圖2.

2 數字PCR檢測儀控制系統的數學模型

注射泵和驅動器的傳遞函數[13-14]:

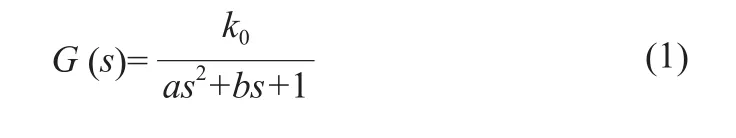
查詢所用電機參數[15],經過換算得到電機的傳遞函數為:

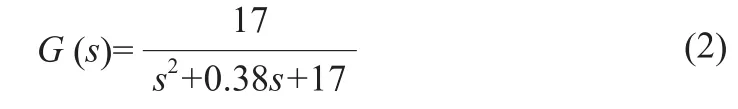
流量傳感器是比例環節[16],設為k1;

液體的流量速度關系[17-18],根據泊肅葉公式:

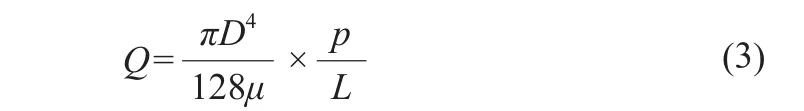
D是管路直徑;p是壓力;L是管路長度;μ是液體的粘度;Q是流量速度.

可以簡化成:

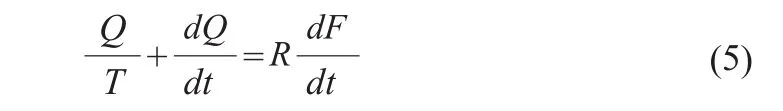
拉普拉斯轉換[19],化得理想狀態下控制對象的傳遞函數:

因此,

根據上述結構的數學模型和傳遞函數,對應圖2的數字PCR檢測儀的雙閉環比值控制系統,整理并化簡框圖,得到框圖,見圖3.

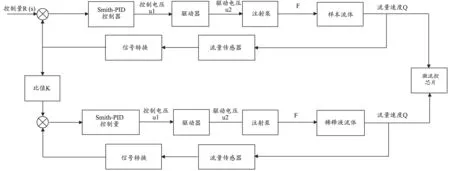
圖2 數字PCR檢測儀液路系統雙閉環比值控制系統結構

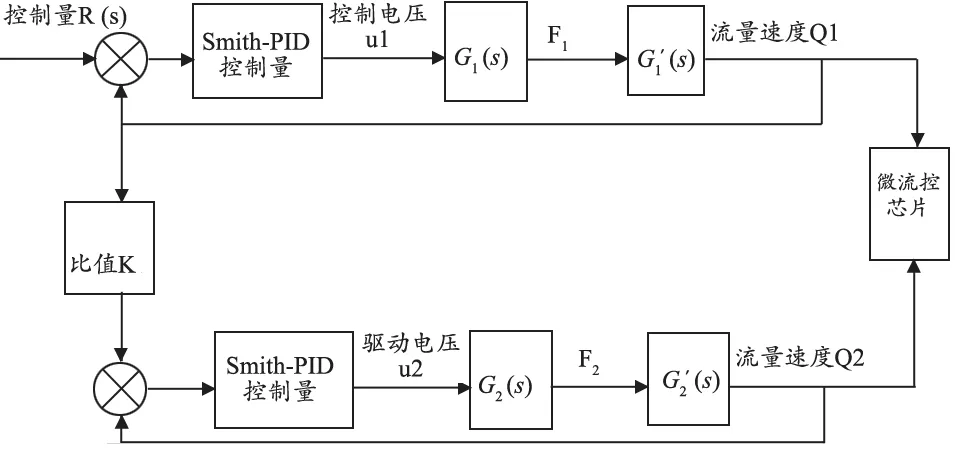
圖3 液路系統雙閉環比值控制系統數學模型

其中:

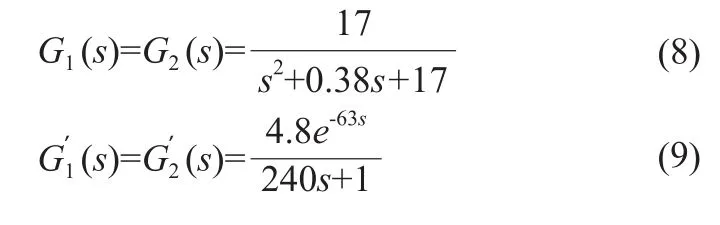
3 數字PCR檢測儀液路系統的Smith-PID控制算法的研究

3.1 Smith-PID控制原理

在兩個閉環回路中主要采用是Smith-PID控制,Smith-PID預估控制是在原來PID控制器的基礎上,針對大時延過程的預估補償,其原理是按照客觀過程的特性預估出一種模型加入到反饋PID控制系統中,使被延時了τ時間的被控量超前反映到調節器的輸入端,使調節器提前動作,從而明顯地減小超調量和加速調節過程.Smith-PID控制系統模型,見圖4.

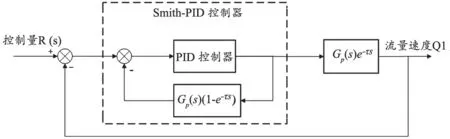
圖4 Smith-PID控制系統模型

對照圖3建立的控制系統及其數學模型,單閉環控制系統中:

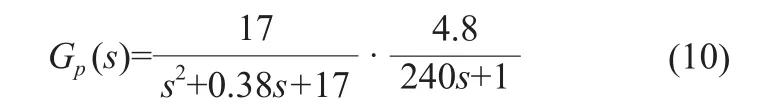
PID控制器的傳遞函數為:

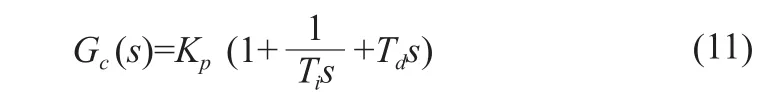
此時單回路的閉環傳遞函數為:

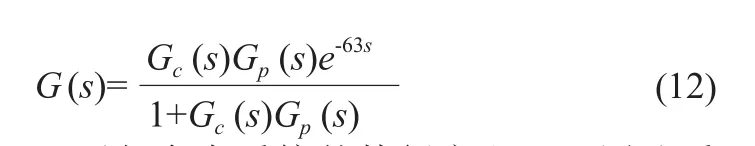
可以看出,已不包含在系統的特征方程里,因此系統性能完全不受純時延環節的影響.從原理上,設計的Smith-PID閉環控制系統完全不存在滯后效應..

3.2 數字PCR檢測儀液路系統的Smith-PID控制算法研究及仿真

Smith-PID控制算法是在PID控制算法基礎上,針對數字PCR檢測儀的滯后問題,把Smith預估控制增加進控制系統里面,目的是減少系統控制的滯后.本文主要在Simulink上仿真來研究算法的優劣,首先在仿真調節基于PID算法的單閉環控制系統[20],見圖5 ,依次調節好比例、積分和微分控制器的參數,不斷修改和仿真,最終得到的響應輸出,見圖6.

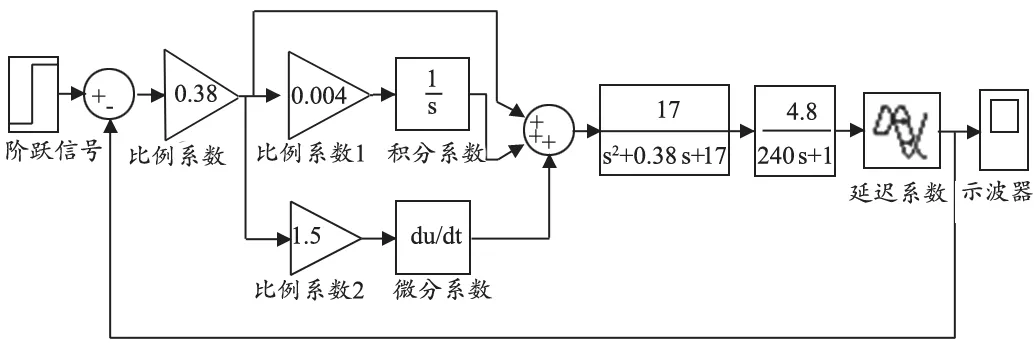
圖5 基于PID算法的單閉環控制系統

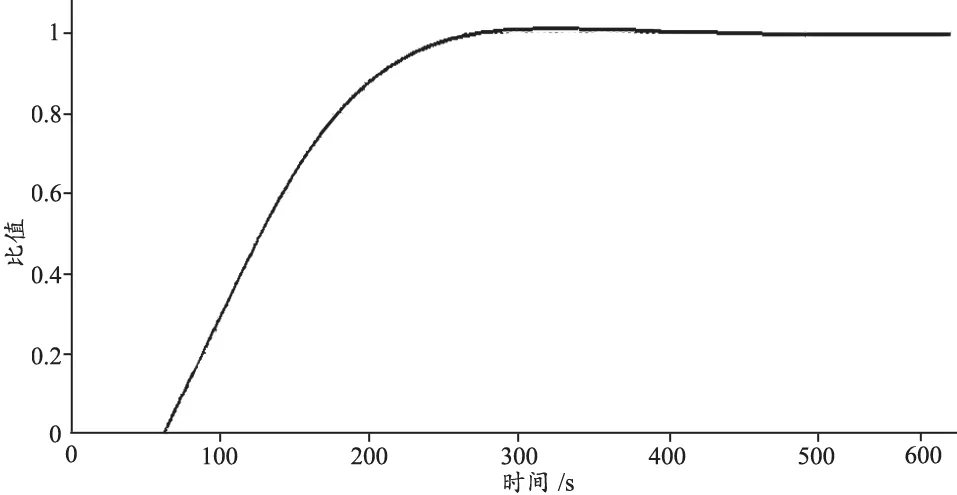
圖6 基于PID算法的單閉環控制系統輸出響應

從以上仿真結果可以看出,系統的靜差為ess=0,超調量σ=1.9%,調節時間ts=285 s,這是整體效果較好的PID參數.在這基礎上如果增加比例環節或者微分環節,加快調節速度,會增加系統從超調量,對于儀器設備來說會有損耗,甚至會對系統的穩定性造成影響.

在圖5設置的較好的PID參數基礎上,增加Smith預估控制環節,見圖7,進一步優化調節PID參數,得到較好的結果,見圖8.

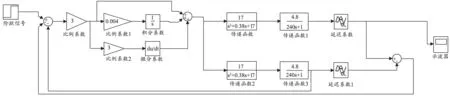
圖7 基于Smith-PID算法的單閉環控制系統

圖8 基于Smith-PID算法的單閉環控制系統輸出響應

系統的靜差為ess=0,超調量σ=0,調節時間ts=134 s.對比圖6和圖8兩種算法輸出響應可以看出,在基于微流控芯片的數字PCR檢測儀的液路系統中,Smith-PID控制算法比傳統的純PID控制算法具有更快的調節速度,縮短調節時間,有效減輕液路系統的滯后現象,控制效果更好.

4 基于Smith-PID的液路控制系統的驗證和結果分析

4.1 基于Smith-PID的數字PCR檢測儀液路雙閉環比值控制系統仿真驗證

在數字PCR檢測儀的液路雙閉環比值控制結構上,Simulink中建立傳統PID控制算法的雙閉環比值控制仿真模型,見圖9,其中結合實際需要,比值為2.仿真效果,見圖10.

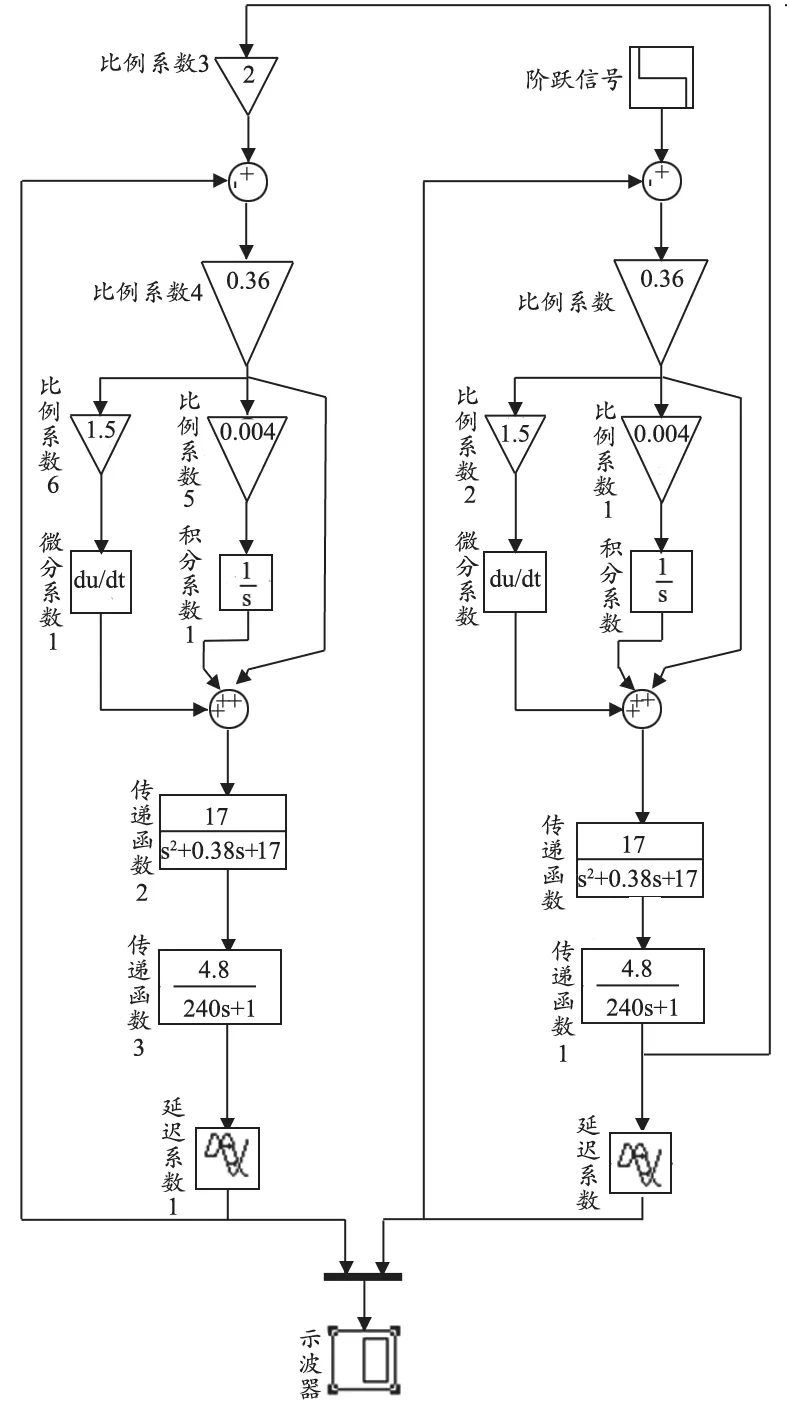
圖9 基于PID算法的雙閉環比值控制系統

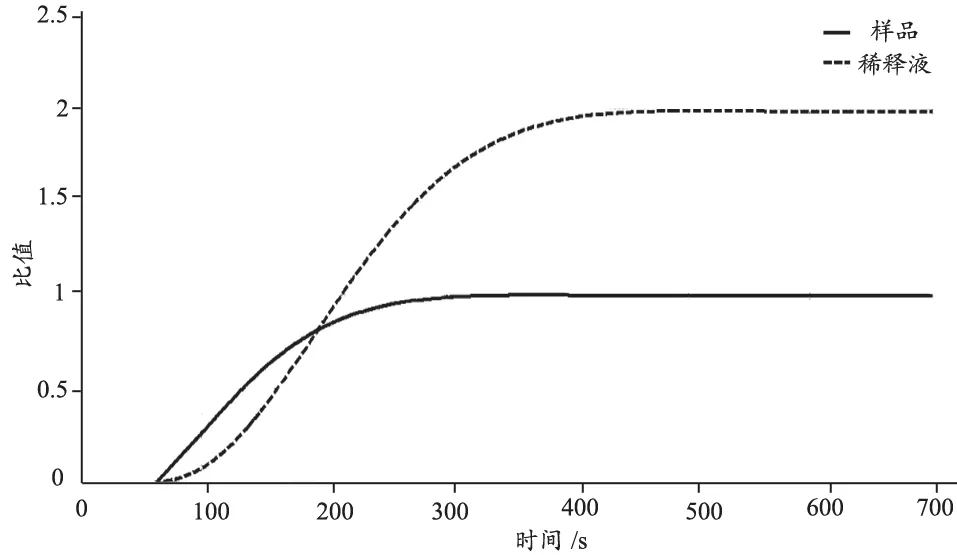
圖10 基于PID算法的雙閉環比值控制系統輸出響應

圖10為傳統PID雙閉環比值控制系統的輸出響應Simulink仿真圖,主回路-樣品控制回路的調節時間為,ts=285 s由于副回路目標值較高是主回路的兩倍,所以會增加調節時間,最終稀釋液調節時間為ts=404 s.

在對數字PCR檢測儀的液路雙閉環比值控制系統結構研究,以及數學模型和單閉環Smith-PID最優參數的基礎上,本文提出基于Smith-PID的數字PCR檢測儀液路雙閉環比值控制系統,建立基于Smith-PID控制算法的雙閉環比值控制仿真系統,見圖11,其中結合實際需要,比值為2.仿真的輸出效果,見圖12.

如圖12為基于Smith-PID算法的雙閉環比值控制系統的輸出響應Simulink仿真圖,其中主回路-樣品控制回路保持了Smith-PID算法的單閉環控制算法的控制效果,樣品的調節時間為ts=134 s,由于副回路目標值較高是主回路的兩倍,所以會增加調節時間,最終稀釋液調節時間為ts=168 s.

從Simulink的仿真圖圖10和圖12對比可以得出,控制系統從傳統PID算法改進到Smith-PID控制算法時候,樣品調節時間從285 s減少到134 s,減少了151 s;稀釋液的調節時間從404 s減少到168 s,減少了236 s,很大提高控制性能.

4.2 數字PCR檢測儀液路控制系統的驗證

根據液路系統雙閉環比值控制原理,系統主要由注射泵、電磁閥、微流控芯片、流量傳感器、管路、接頭等組成.系統工作如下:樣本注射泵和稀釋液注射泵對液體推進,樣品液和稀釋液進入微流控檢測芯片,根據樣品的流量,計算機控制注射泵的速度,按比值調節稀釋液的流量;調節過程中,一方面樣品流量根據設定值,運用Smith-PID控制算法,不斷調節達到目標值,另一方面,稀釋液根據樣品流量,運用Smith-PID控制算法,不斷調節達到樣品流量的某個比值.

在數字PCR檢測儀的測試液路系統中,采用傳統PID的雙閉環比值控制,如同圖9的仿真模型,采集的流量輸出響應得到響應曲線,見圖13.

圖13上可以得出傳統PID控制系統性能參數,控制系統中樣品調節時間為ts=302 s,稀釋液調節時間為ts=358 s,與仿真的輸出響應基本吻合;此外,可能因為積分飽和的原因,存在約為10%輸出靜差.

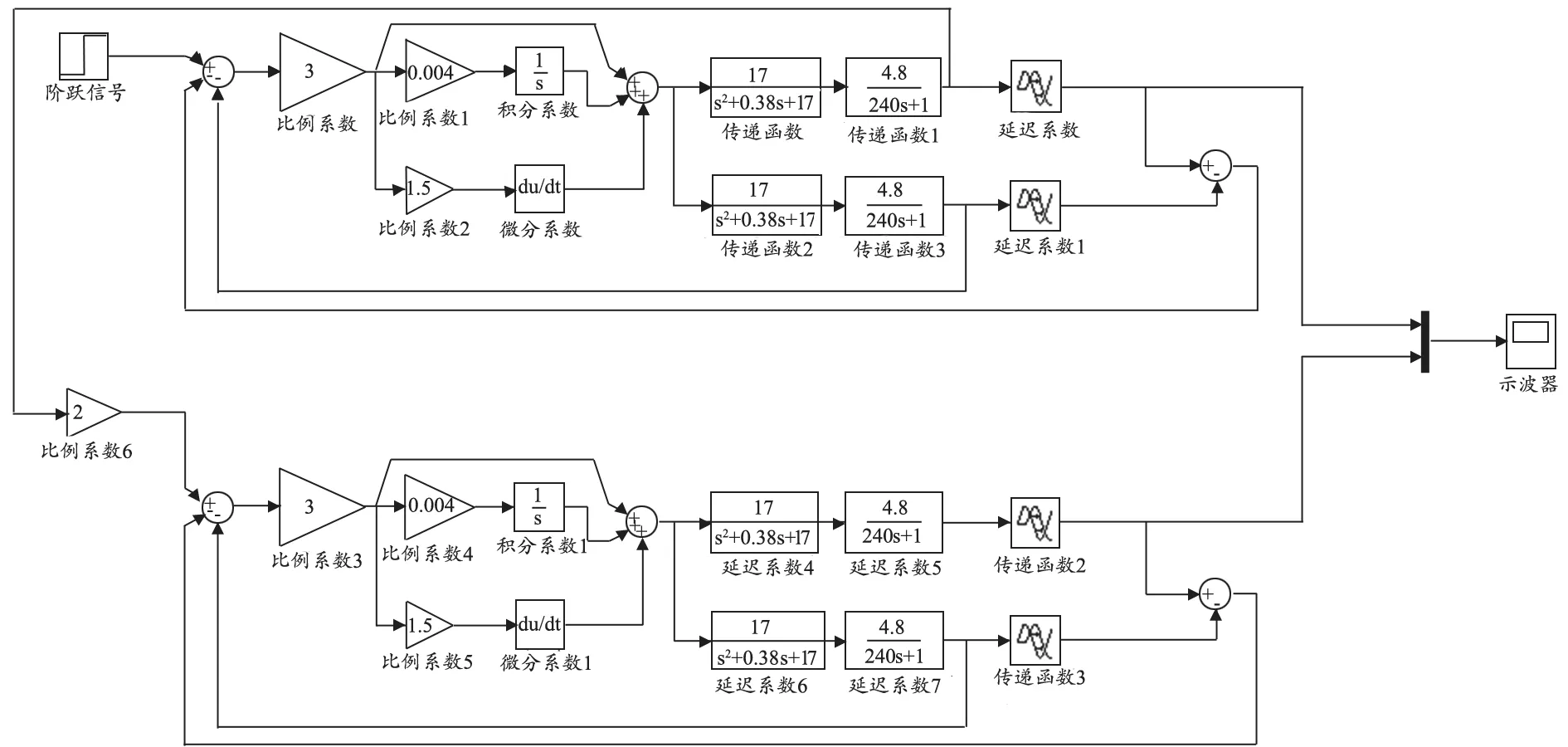
圖11 基于Smith-PID算法的雙閉環比值控制系統

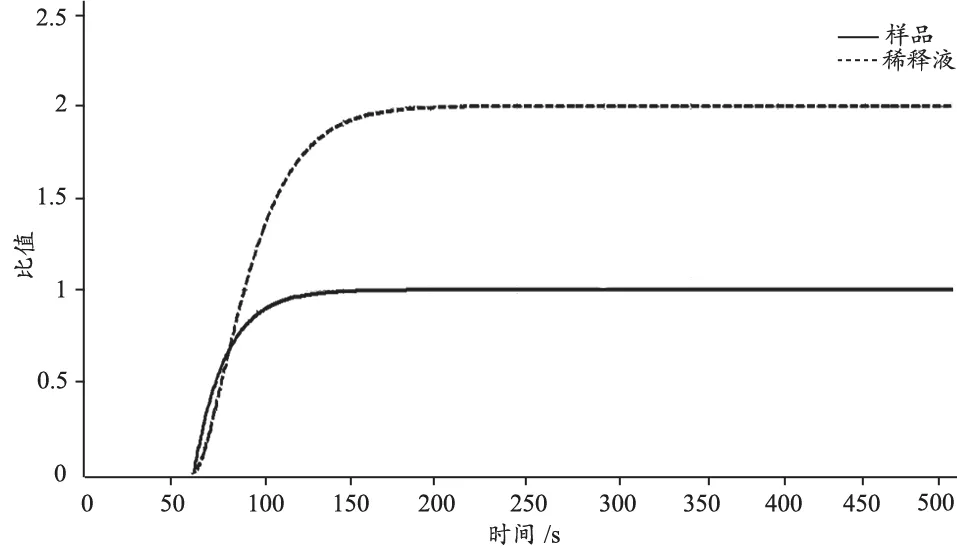
圖12 基于Smith-PID算法的雙閉環比值控制系統輸出響應

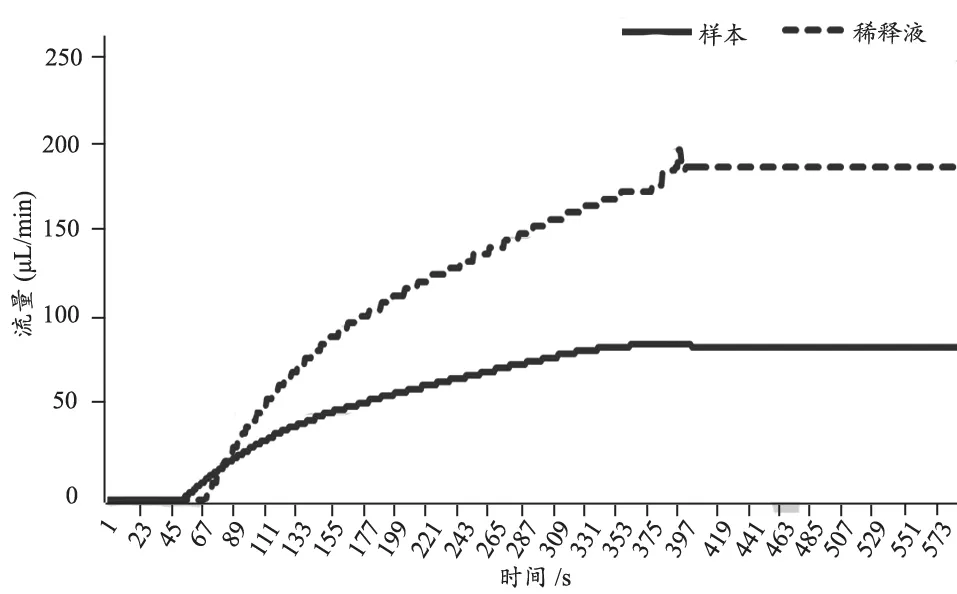
圖13 傳統PID控制下液路流量的輸出響應

在數字PCR檢測儀的測試液路系統中,采用Smith-PID的雙閉環比值控制,如同圖11仿真模型,采集的流量輸出響應得到響應曲線,見圖14.

如圖14的數字PCR檢測儀的液路流量響應曲線,趨勢上與仿真一致,但是在樣本回路即主回路中,調節時間為ts=111 s,中間由于電機脈沖和傳感器的影響,輸出流量存在一定的脈動,但是脈動沒有超過2%,對于儀器的檢測效果沒有影響;而稀釋液回路即副回路中,實際上的超調時間ts=193 s,此誤差更多是因為在樣本進入芯片過程中對于稀釋液回路的影響,本文在建模過程中簡化了樣本與稀釋液之間的作用.

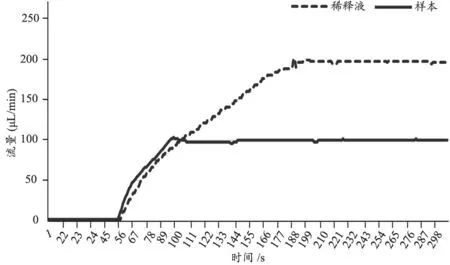
圖14 Smith-PID控制下液路的輸出響應

4.3 驗證的結果分析及討論

從式(3)泊肅葉公式可以看出,在基于微流控的數字PCR液路系統中,因為內徑小在幾十微米的數量級,而且油的粘度大,粘度大約為水粘度的300多倍,這樣的對象系統下,流體的阻力較大大,流體滯后現象較為嚴重;從圖13也可以看出,在樣品給定階躍為100,稀釋液與樣品比值為2的控制給定值下,在微流控芯片的液路控制中,采用的傳統PID控制存在著響應速度仍然較慢,穩態誤差較為嚴重.

同樣的給定值和比值控制,對比圖13和圖14可以看出,與傳統的PID控制器相比,加入了Smith-PID控制器的PCR檢測儀的液路系統在性能上有很大的提高,樣品的調節調節時間從由302 s減少為111 s,縮短了約2/3時間;稀釋液的調節時間由359 s減少為193 s,縮短了約1/3時間;輸出的靜態誤差從10%減小到2%,減少了8%.此外,縮短調節時間不僅提高儀器的整體性能,而且還有利于消減積分飽和,減小系統的穩定誤差,使得系統更加穩定.

本文主要針對微流控芯片中流體控制的大阻力、大滯后的問題,提出與傳統液路系統不同的新型微流控液路系統中的滯后問題的解決方法,采用Smith-PID控制比起常用的純PID也有更好的效果.不足之處,本文研究的算法沒法克服PID本身的缺點,以及Smith預估對于模型的要求,如果建立的模型不夠準確或者簡化某些環節,可能存在圖14中的穩態偏差.因此,在使用改算法和控制系統,需要對于對象的數學模型的深入了解和長時間的實際試驗及修正.

5 總結

針對基于微流控芯片的數字PCR檢測儀中,相較于傳統PID控制下的液路系統流量的控制,Smith-PID控制器能夠更好的克服流體的大阻力、大滯后問題.引入Smith-PID控制器的液路雙閉環比值控制系統,較好的克服微流控芯片中流體的大阻力、大滯后問題;同時相較于傳統的PID控制下,輸出樣品的調節時間縮短了約2/3,稀釋液的調節時間縮短了約1/3, 穩態誤差減小8%,減少了調節時間,提高了調節的效率,有利于減小積分飽和對于系統的影響,提高系統輸出流量的精度和穩定性.因此,在數字PCR檢測儀的液路中,引入基于Smith-PID控制器的雙閉環比值液路控制系統,在系統的穩定性、準確性、快速性都有很好的控制效果.

[1] 吳堅,曹文祺.聚合酶鏈式反應(PCR)熒光檢測研究[J].計量學報,2002,23(2):151-156.

[2] 薛巍,姜雯,蘇榮國.微流控芯片檢測技術進展[J].化學分析計量,2007,16(3):77-79.

[3] 馮眾穎,周兆英,葉雄英.微流體驅動與控制技術研究進展[J].液壓與氣動,力學進展,2002,32(1):1-15.

[4] Sugiura S,Edahiro J,Kikuchi K,et al.Pressure-driven perfusion culture microchamber array for a parallel drag cytotoxicity assay[J].Biotechnol Bioeng,2008,100(6):1156-1165.

[5] 王志超,董明利,劉超.基于模糊PID的流式細胞儀液流主從控制系統[J].液壓與氣動,2017,(2):45-50

[6] 趙國普.液壓元件試驗臺計算機輔助檢測系統的研究[J].機床與液壓,1999,5:77-80.

[7] El-Ali J,Sorger PK,Jensen KR.Cells on chips[J].Nature,2006,442(7701):403-411.

[8] Muto T,Yamada H,Suematsu Y.Digital control of hydraulic actuator system operated by differential pulse width modulation[J].JSME Int,1990,33(4):641-648.

[9] Owens DH,Raya A.Robust stability of smith predictor controllers for time delay systems[J].IEE Proc. Part D,1982,129(6):298-304.

[10] 張峻穎,楊馬英,謝啟.含有純滯后系統的控制方法[J].控制工程,2002,9(6):91-93.

[11] 程啟明,王勇浩.基于Smith預估的模糊/PID串級主汽溫控制系統仿真[J].電工技術學報,2007,22(3):143-147

[12] 陳莉,張鋒.串級-Smith預估控制在溫度大滯后系統中的應用[J].儀表技術,2007,(2):37-39.

[13] 程樹康,劉寶延.步進電動機及其驅動控制系統[M].哈爾濱:哈爾濱工業大學出版社,2007.

[14] 姜德美,謝守勇,甘露萍.步進電機啟動控制算法設計[J].西南大學學報(自然科學版),2007,(5):129-132

[15] 王邦繼,劉慶想,周幕,等.步進電機速度曲線的設計與FPGA實現[J].微電機,2012,45(8):67-71.

[16] 耿德根.AVR高速嵌入式單片機原理與應用[M].北京:北京航空航天大學出版社,2002.

[17] 邵裕森.過程控制及儀表[M].上海:上海交通大學出版社,2008.

[18] 陳偉,張聯志,徐蒙.灌漿壓力穩定性控制的流體力學模型研究[J].應用力學學報,2013,30(1):65-69.

[19] 王建輝,顧樹生.自動控制原理[M].北京:清華大學出版社,2005.

[20] 陳永清,黃金.基于Simulink的復合節流調速系統仿真分析[J].液壓與氣動,2011,(10):15-17.

本文編輯 袁雋玲

Design of Double Closed Loop Ratio Control System of the Digital PCR Detector Based on Smith-PID

CHEN Qingming, LIU Jinglong, LI Dongmei
a.Department of Precision Instrument; b.Department of Electronic Information, Guangdong Shunde Industrial Design Institute(Guangdong Shunde Innovative Design Institute), Foshan Guangdong 528311, China

The precision, speed and stability of the liquid output of the liquid system are the basis of the function of the digital PCR detector. In order to solve the problem of large resistance and large delay in the liquid circuit system of the digital PCR detector,the structure of the double closed loop control system based on the Smith-PID algorithm was proposed. A double closed loop ratio control system was constructed according to the injection pump, the control object model and Smith controller principle. In addition,modeling and simulation was performed on the system for the use of Simulink, and a better response curve was obtained compared to the traditional PID. In the digital PCR detector liquid circuit system verification, we found that compared with the traditional double closed loop liquid path of PID control, the settling time of the double closed loop ratio control system Smith-PID control samples reduced 2/3, dilution adjustment time reduced 1/3, the steady-state error reduced 8%. In conclusion, the Smith-PID control algorithm can improve the rapidity, accuracy and stability of the flow output system.

digital PCR; Smith-PID control; double closed loop ratio control; liquid system

TP27;TP774 < class="emphasis_bold">[文獻標識碼] A

A

10.3969/j.issn.1674-1633.2017.10.009

1674-1633(2017)10-0033-06

2017-05-08

2017-05-23

作者郵箱:653911982@qq.com