徑向點插值法局部形參的改進校準方法

禹忠 楊劉偉 柯熙政

(1. 西安理工大學,西安 710048;2. 西安郵電大學,西安 710121)

徑向點插值法局部形參的改進校準方法

禹忠1,2楊劉偉2柯熙政2

(1. 西安理工大學,西安 710048;2. 西安郵電大學,西安 710121)

徑向點插值法(Radial Point Interpolation Method,RPIM)中基函數形參、支持域大小和平均節點間距等因素直接影響算法的精度與計算效率,而過小形參會引起插值不穩定現象. 針對此問題,提出一種基于局部形參校準法(Local Shape Factor Calibration Method,LSFCM)改進的形參優化算法,研究RPIM應用于電磁場問題中插值精度的影響因素,在不同形參、支持域大小和節點距離時的全局均方根插值誤差曲線上,根據插值精度和計算效率靈活選擇全局形參,簡化形參設置與節點插值計算過程,提高計算效率. 數值試驗結果驗證了所提方法的有效性.

無網格法;徑向點插值;徑向基函數;支持域;形參校準

引 言

近年來,徑向點插值法(Radial Point Interpolation Method,RPIM)成為時域電磁場數值計算方法的研究熱點之一. 相對于目前廣泛應用的時域有限差分[1](Finite Difference Time Domain ,FDTD)法和有限元法[2](Finite Element Method,FEM),其不需要生成復雜的網格結構, 可以靈活設置節點位置和密度,網格法中的網格重建亦可以通過自適應的節點分布來代替,因此在處理復雜多尺度結構問題時具有很多優勢[3-6].

RPIM是一種高效的數值計算方法,其計算點場值由支持域中其他節點場值采用徑向基函數插值近似獲得,因其優異的插值特性被引入于電磁場領域求解偏微分方程問題,但RPIM中基函數形參、支持域大小和平均節點間距等因素對插值精度影響較大. 傳統RPIM參數選擇優化算法的研究集中在交叉驗證(Leave-One-Out Cross Validation,LOOCV)法,但其多適用于全局插值或分區域插值[7-10]．局部形參校準法(Local Shape Factor Calibration Method,LSFCM)雖可獲取各支持域最優形參[11],但每個支持域設置不同形參較為繁瑣.

本文中,采用改進的LSFCM設置校準函數,RPIM計算支持域插值,結合均方根誤差(Root Mean Square Error,RMSE)函數,計算獲得不同情況下全局插值RMSE曲線,確定合適的最大誤差,即可獲得全局最優形參或符合精度的形參范圍. 通過分析RPIM應用于二維交錯節點分布時,不同支持域大小、不同節點間距對插值精度的影響,測試各種情況下獲得的最優形參范圍,為RPIM的形參選擇提供參考.

1 徑向點插值法

計算域中位置X處場分量u(X)可由其支持域中N個節點插值近似[12]為

=rT(X)a+pT(X)b.

(1)

式中:rn(X)為徑向基函數;pm(X)為單項式基函數;an和bm為相應插值系數.

實際應用中存在多種徑向基函數,而求解電磁場問題時,高斯徑向基函數具有更好的性能,其為節點距離的指數函數,即

(2)

式中:形參αc控制基函數平滑度及插值精度;dc表示支持域中節點的平均距離.

低階多項式基函數項pm(X),可改善局部基函數的收斂特性,增加插值近似的精度.

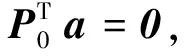
(3)

式中,插值系數矢量a和b由下式計算:

(4)

式(4)代入式(1),即可獲得RPIM形函數Φ(X):

=Φ(X)Us.

(5)

形函數Φ(X)滿足Kronecker delta函數特性,保證了對節點場值的準確擬合插值. 形函數沿κ=x,y方向空間導數可表示為

=?κΦ(X)Us.

(6)

RPIM應用于一階麥克斯韋微分方程時,其形式類似于FDTD,時域微分由中心差分形式離散,而空間導數則由式(6)插值近似獲得,二維TM波更新方程形式如下:

(7)

2 插值精度的影響因素

2.1徑向基函數

目前,應用于無網格RPIM中的徑向基函數有很多種[13]:復合二次(Multi-Quadrics, MQ)函數、高斯(Exponential, EXP)函數、薄板樣條(Thin Plate Spline, TPS)函數、對數型函數和緊支徑向基函數(Compactly Supported Radial Basis Function, CSRBF)等. 其中MQ和EXP應用最為廣泛,MQ基函數多用于固體力學領域,而EXP基函數更多應用于電磁場領域. 這些基函數均含有部分形參,且形參對其插值精度影響較大. EXP基函數中,形參αc控制徑向基函數的平滑度,如圖1所示[10].

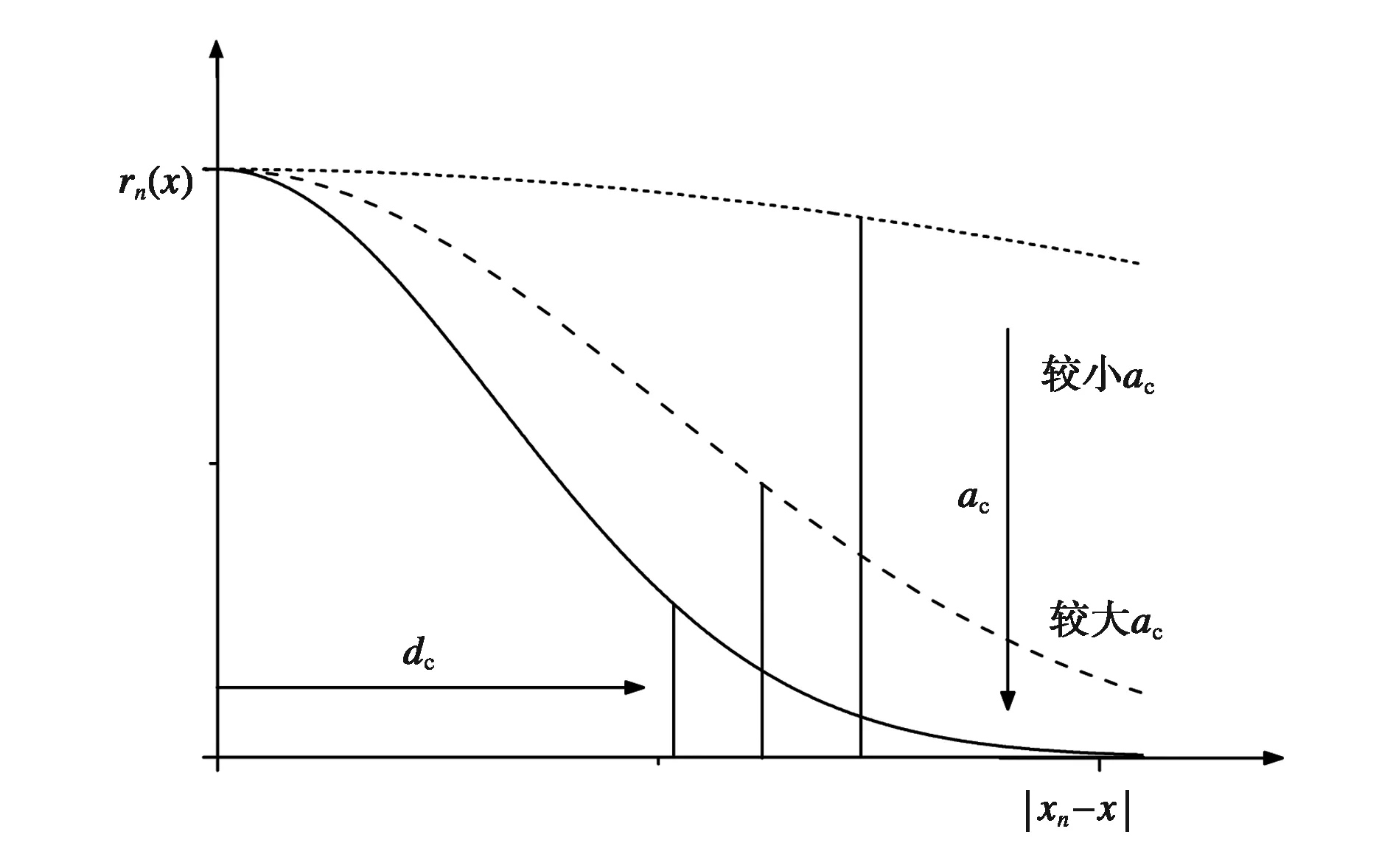
圖1 形參對EXP基函數的影響及支持域選擇

研究表明:αc越小,EXP基函數越平坦,RPIM插值近似精度越高;但隨著αc趨于0,式(4)中求解形函數的矩量矩陣G條件數急劇增大(指數階),從而導致矩陣求逆困難,徑向點插值會在αc趨于零時產生嚴重的不穩定現象. 因此,最優形參αc的選擇是對穩定性和精度的綜合考慮.

2.2最優形參

經過研究,RPIM全局最優形參αc通常選擇接近于0的較小值,一般小于1,如取αc=0.01[12],但由于矩陣求逆困難問題,此形參值并非對每一個支持域都可以獲得較好的插值精度. 因此,Rippa、Kaufmann等[5-6,14-15]采用了LOOCV法進行RMSE分析,獲得了全局或分區域插值最優形參. 而Machdo等[11]通過實驗獲得最優形參,分別測試了αc=0.1、αc=7.4和αc=8.5的百分比誤差,并提出了LSFCM,獲得各支持域的局部最優形參,避免矩陣求逆困難問題,減小了插值誤差．

相對于之前的LOOCV法,本文中改進的形參校準方法選取插值誤差曲線極小值點作為最優形參,避免了過小形參引起的矩陣求逆困難問題;又不同于局部形參校準法,采用了全局插值誤差曲線,獲得計算域統一的最優形參,簡化了形參設置與支持域插值計算過程.

3 局部形參校準方法

本文采用改進的LSFCM設置校準函數,通過RPIM計算支持域插值,結合RMSE函數,計算不同情況下全局插值誤差,確定合適的最大誤差即可獲得最優形參值選擇范圍. 并進一步分析二維交錯節點分布時,電磁場計算中不同支持域大小、不同節點距離對插值精度的影響,測試各種情況下獲得的最優形參范圍,為RPIM的應用提供參考.

3.1改進的形參校準方法

改進的LSFCM首先設置二維計算域Ω中校準函數:

C(ui)=sin(Kxi)cos(Kyi).

(8)

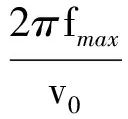
采用RPIM局部方案對計算域各節點插值近似,為確定最優形參值αc,定義各節點插值誤差為

ξi(c)=C(c,ui)-C(ui).

(9)

式中,C(c,ui)為形參αc取c時,對校準函數C(ui)計算域中第i個節點的插值,由式(1)獲得. 取計算域各節點插值誤差,計算全局插值誤差:

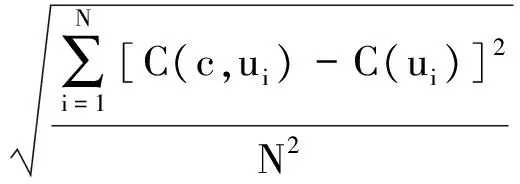
(10)

獲得插值誤差曲線,形參優化方法通過檢測誤差函數極小值點,即可獲得全局的最優形參值或符合精度要求的形參選擇范圍．其整個計算域只需設置同一個最優形參,可以簡化形參設置與節點插值計算過程,提高計算效率,優化RPIM．

3.2數值分析

本文采用電磁場問題交錯節點分布[16-17],設置校準函數中最高頻率fmax=3 GHz,計算域大小為600×600節點.

3.2.1 支持域半徑對插值精度影響

首先考慮支持域半徑對插值精度的影響,支持域分別選擇4節點(1.0dc)、12節點(2.0dc)、32節點(3.0dc)、80節點(5.0dc),節點間距選擇λ/20(5 mm),獲得了不同支持域半徑時插值誤差曲線,如圖2所示．

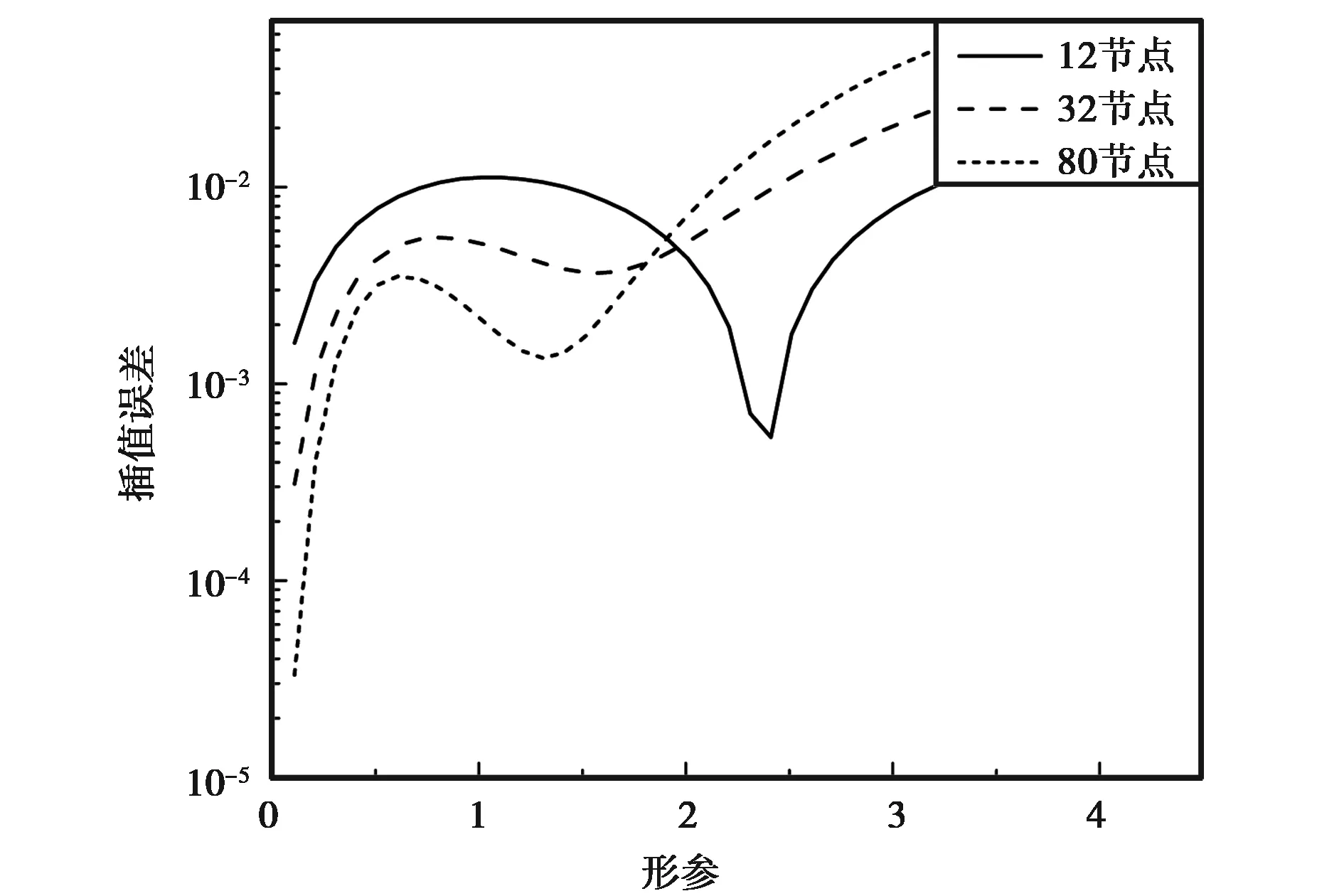
圖2 支持域半徑對插值精度影響

分析數據可知:形參αc選擇0.01,支持域選取12節點時,插值誤差為1.26×10-4,而32節點和80節點時均出現不穩定現象;形參αc選取0.1時,支持域半徑越大,節點數越多,插值誤差越小,80節點時可達到3.31×10-5;檢測誤差曲線極小值點,支持域取12節點,極小值點αc=2.4時,其插值誤差為5.37×10-4,為三者中最小,32及80節點時,支持域半徑越大,極小值點越靠近零值,且插值誤差越小,分別達到3.65×10-3(αc=1.6)和1.35×10-4(αc=1.3);從總體分布來看,支持域半徑越大,誤差函數在形參取零值到極小值點間的誤差越小,而取大于極小值點時,誤差函數正好相反. 支持域選取4節點時,由于支持域半徑過小,其插值誤差為1.22×10-2,插值精度極低,不建議采用.

綜合以上分析可獲得以下結論:1) 形參取接近零值時,αc越小,插值精度越高;2) 增大支持域半徑,可提高形參取接近零值時的插值精度,但αc過小會引起插值不穩定現象;3) 形參優化方法中,形參取誤差函數極小值點,可有效避免過小形參引起的插值不穩定現象,并可達到近零點的計算精度;4) 增大支持域半徑,可減小誤差函數極小值點插值誤差,但對插值精度的提升不明顯;5) 綜合考慮計算精度和計算效率,12節點(2.0dc)為支持域半徑最優選擇,而交錯節點分布下支持域選擇1.5dc～3.0dc時,計算效率較高,插值誤差較小.

3.2.2 平均節點間距對插值精度的影響

首先選取支持域半徑為2.0dc(12節點),平均節點間距分別設置為λ/10(10 mm)、λ/14(7 mm)、λ/20(5 mm)、λ/30(3 mm)、λ/50(2 mm),應用形參優化方法,分別獲得不同平均節點間距時插值誤差曲線,如圖3所示.

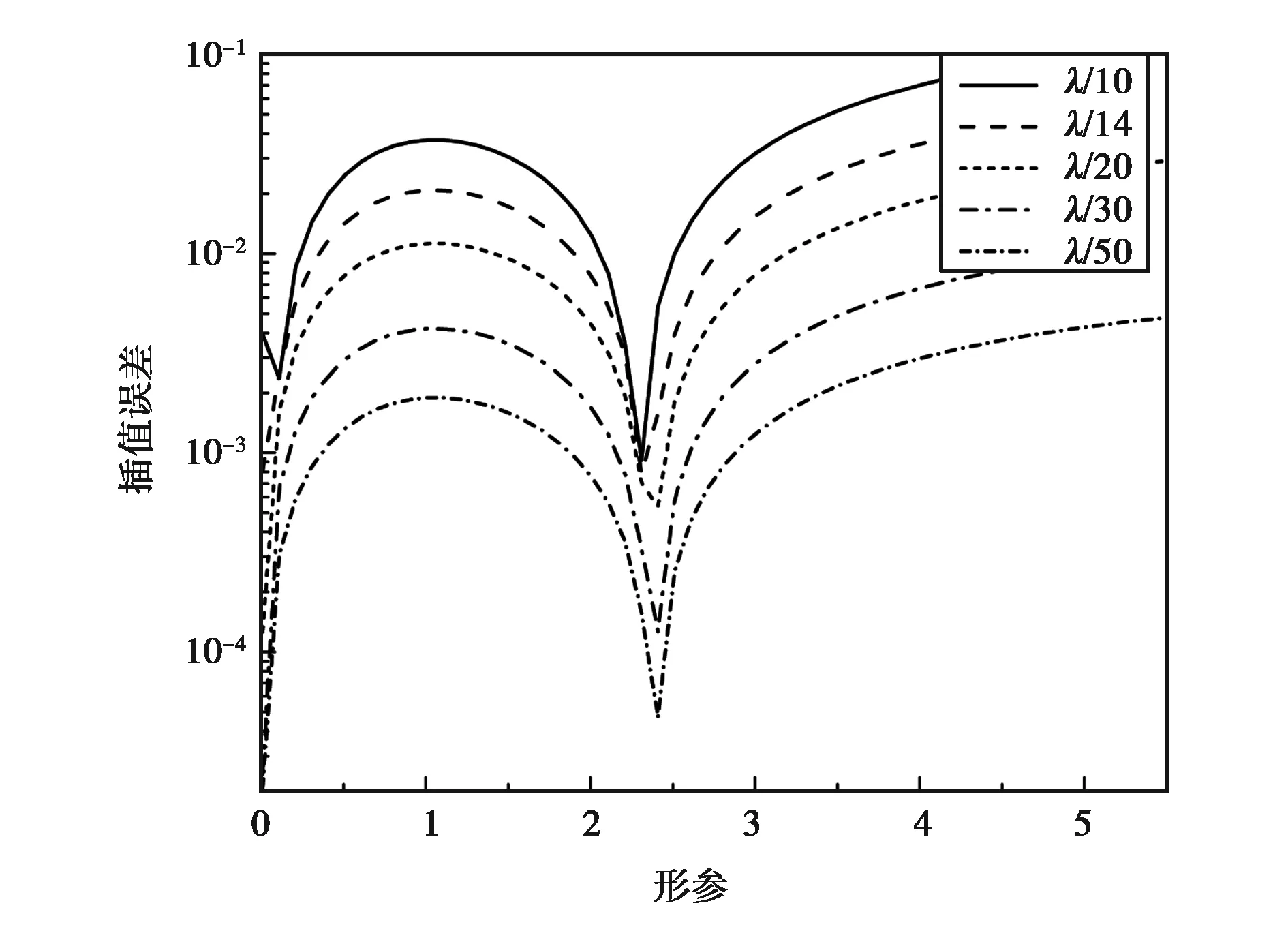
圖3 平均節點間距對插值精度影響

分析數據可知:形參αc選取0.01時,插值誤差最小達2.07×10-5,最大為3.93×10-3,均可穩定插值;而選取極小值點時,不同平均節點間距的極小值點集中于2.3～2.4,且插值誤差最小為4.69×10-5,最大為9.17×10-4,均可達到較高精度．總體來看,平均節點間距越小,插值誤差越小.

綜合以上分析可得以下結論:1) 平均節點間距越小,插值誤差越小;2) 平均節點間距對極值點位置影響較小,即對最優形參值影響較小;3) 采用形參優化方法獲得極值點最優形參可獲得較高的插值精度.

3.2.3 數值驗證

綜合考慮以上結論,選取支持域半徑為2.0dc(12節點),平均節點間距為λ/20(5 mm),其插值誤差為5.37×10-4,具有較高插值精度,對校準函數應用RPIM插值近似,獲得了良好效果,如圖4所示.

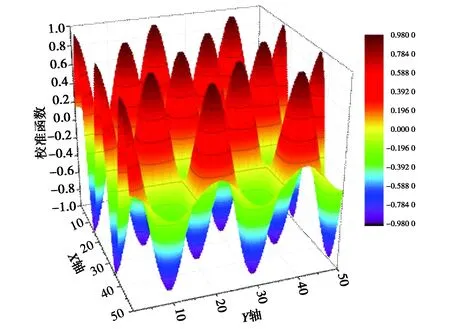
(a) 校準函數

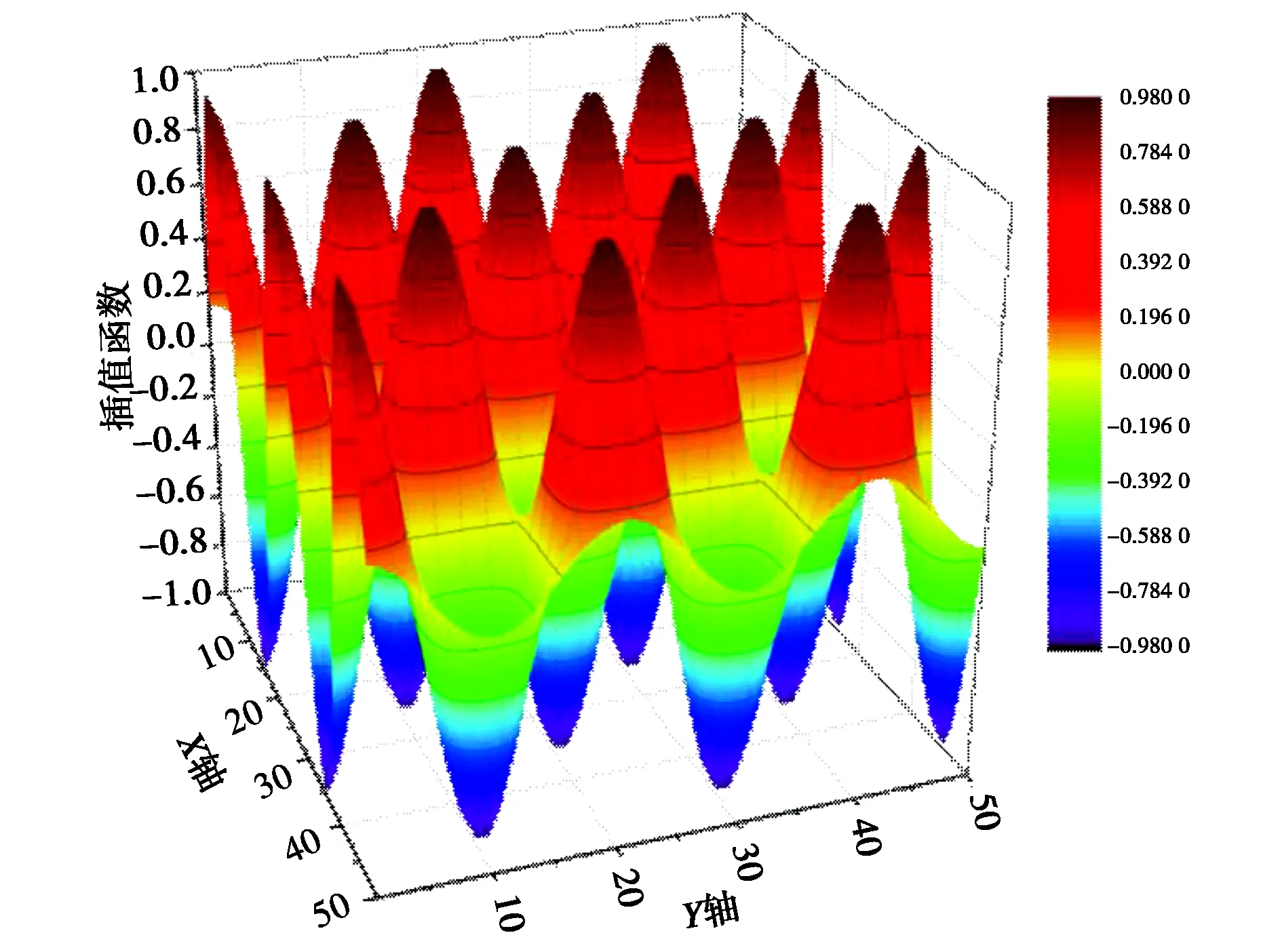
(b) 徑向點插值圖4 校準函數驗證

為驗證形參優化方法,參考文獻[4]設置二維計算域中高斯點輻射源:

(11)

式中:τ=5.33e-9s;t0=0.8τ. 采用規則交錯節點分布,支持域半徑為2.0dc(12節點),節點距離d=0.01 m,計算域設置足夠大(600×600節點)以避免反射誤差,在距離輻射源一倍節點距離處設置觀察點. 參考解析解形式如下:

(12)

由RPIM和FDTD方法獲得的時域結果如圖5所示．與FDTD對比,RPIM更為接近解析解,具有較好精度.

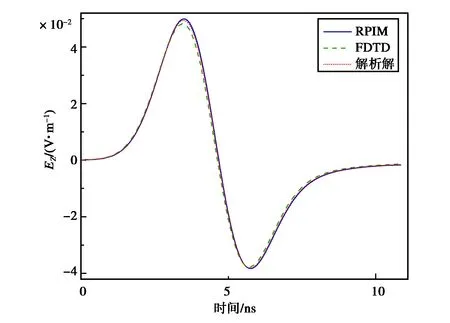
圖5 觀察點時域波形

表1中列出RPIM和FDTD的計算消耗及節點插值的均方根誤差．對比數據可知,在相同的時間步進和節點數時,RPIM內存消耗略微高于FDTD,但計算時間遠小于FDTD,且插值誤差亦小于FDTD.

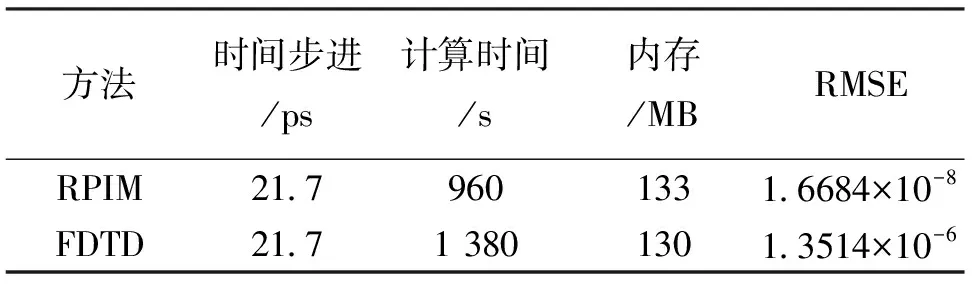
表1 計算效率

注:文中所有結果均使用配置為主頻2.93 GHz、Intel i5 CPU、4GB RAM的計算機獲得,采用Intel MKL LAPACK進行矩陣運算和方程組求解.

4 結 論

本文采用LSFCM改進的形參優化方法,解決RPIM應用于求解電磁場問題中的最優形參選擇問題. 主要分析了采用二維交錯節點分布時,支持域半徑和平均節點間距等因素對插值精度的影響,并通過數值試驗驗證了形參優化方法的有效性.

相對于目前主要采用的實驗方法或交叉驗證法,改進的形參校準方法由RMSE函數極小值點獲取最優形參,更準確快捷,避免了過小形參引起的插值不穩定現象;又不同于之前的形參校準法,其計算域選取統一的最優形參,簡化了誤差計算與形參設置,提高了計算效率.

數值試驗結果表明,二維交錯節點分布時,支持域半徑選擇1.5dc～3.0dc可獲得較高精度,而支持域半徑選取2.0dc(12節點)為最優選擇. 平均節點間距越小精度越高,可根據計算效率和內存消耗靈活選擇,建議平均節點間距選取λ/20,可減少內存消耗,同時可獲得較高的插值精度. 本方法亦可擴展到三維領域,而完全不規則節點分布的應用需要進一步研究．

[1] 蘇卓, 譚峻東, 張俊, 等. 基于高階時域有限差分算法的電磁波傳播計算[J]. 電波科學學報, 2014, 29(3): 431-436.

SU Z, TAN J D, ZHANG J, et al. An electromagnetic wave propagator based on higer-order FDTD method[J]. Chinese journal of radio science, 2014, 29(3): 431-436. (in Chinese)

[2] 彭文峰, 宛汀, 郁美艷. 復雜媒質目標電磁散射問題的有限元分析[J]. 電波科學學報, 2013, 28(1): 76-81.

PENG W F, WAN T, YU M Y. Applying the finite element method to analyze EM scattering of the complex media targets[J]. Chinese journal of radio science, 2013, 28(1): 76-81. (in Chinese)

[3] ZHANG X, CHEN Z D, YU Y. Numerical simulation of coupled transient electrothermal fields with the meshless RPIM[C]//IEEE International Symposium on Antennas and Propagation &USNC/URSI National Radio Science Meeting, 2016: 625-626.

[4] ZHANG X, CHEN Z, YU Y. An unconditional stable meshless ADI-RPIM for simulation of coupled transient electrothermal problems[J]. IEEE journal on multiscale and multiphysics computational techniques, 2016, 1: 98-106.

[5] TANAKA Y, WATANABE S, OKO T. Study of eddy current analysis by a meshless method using RPIM [J]. IEEE transactions on magnetics, 2015, 51(3): 1-4.

[6] ZHU H, GAO C, CHEN H. An unconditionally stable radial point interpolation method based on Crank-Nicolson scheme [J]. IEEE antennas and wireless propagation letters, 2017, 16: 393-395.

[7] RIPPA S. An algorithm for selecting a good value for the parameter c in radial basis function interpolation[J]. Advances in computational mathematics, 1999, 11(2): 193-210.

[8] FASSHAUER G E, ZHANG J G. On choosing “optimal” shape parameters for RBF approximation [J]. Numerical algorithms, 2007, 45(1): 345-368.

[9] WEI YX, XU L, CHEN X Q. The Radial Basis Function shape parameter chosen and its application in engineering [C]//IEEE International Conference on Intelligent Computing and Intelligent Systems. Shanghai, November 20-22, 2009: 79-83.

[10] KAUFMANN T, ENGSTROM C, FUMEAUX C, et al. Eigenvalue analysis and longtime stability of resonant structures for the meshless radial point interpolation method in time domain[J]. IEEE transactions on microwave theory and techniques, 2010, 58(12): 3399-3408.

[11] MACHADO P L, OLIVEIRA R, SOUZA W C, et al. An automatic methodology for obtaining optimum shape factors for the radial point interpolation method [J]. Journal of microwaves, optoelectronics and electromagnetic applications, 2011, 10: 389-401.

[12] WANG J G, LIU G R. A point interpolation meshless method based on radial basis functions [J]. International journal for numerical methods in engineering, 2002, 54(11): 1623-1648.

[13] LIU G R, GU Y T. An introduction to meshfree methods and their programming [M]. Netherlands: Springer, 2005: 276-283.

[14] FASSHAUER G F. Meshfree approximation methods with MATLAB[M]. World Scientific, 2007: 376-382.

[15] KAUFMANN T, ENGSTROM C, FUMEAUX C. Residual-based adaptive refinement for meshless eigenvalue solvers[C]//International Conference on Electromagnetics in Advanced Applications. Sydney, September 20-24, 2010: 244-247.

[16] LEE J F, LEE R, CANGELLARIS A. Time-domain finite-element methods[J]. IEEE transactions on antennas & propagation, 1997, 45(3): 430-442.

[17] BARBER C B, DOBKIN D P, HUHDANPA A H. The quickhull algorithm for convex hulls[J]. ACM transactions on mathematical software, 1996, 22(4): 469-483.

禹忠(1973—),男,陜西人,副教授,主要研究方向為計算電磁學、天線與微波器件、無線通信信道、移動互聯網技術．

楊劉偉(1990—),男,陜西人,碩士研究生,研究方向為計算電磁學．

Theoptimizedcalibrationmethodforthelocalshapefactorsofradialpointinterpolationmethod

YUZhong1, 2YANGLiuwei2KEXizheng2

(1.Xi’anUniversityofTechnology,Xi’an710048,China;2.Xi’anUniversityofPosts&Telecommunication,Xi’an710121,China)

In the radial point interpolation method (RPIM), the shape factors such as the parameters of basis function, the support domain size and the average node distance directly affect the interpolation precision and computational efficiency, and the small shape parameter may lead to interpolation instability. In order to optimize parameter selection in RPIM, the algorithm based on the local shape factor calibration method(LSFCM)is proposed in the electromagnetic field problem. The global root mean square (RMS) interpolation error curve with different support domain size, node distance and different parameters can simplify the process of the shape parameter selection and node interpolation. The numerical results show the algorithm has improved the interpolation precision and computational efficiency.

meshless method;radial point interpolation method; radial basis functions; support domain; shape parameter calibration

禹忠, 楊劉偉, 柯熙政.徑向點插值法局部形參的改進校準方法[J]. 電波科學學報,2017,32(4):410-415.

10.13443/j.cjors.2017033001

YU Z, YANG L W, KE X Z. The optimized calibration method for the local shape factors of radial point interpolation method[J]. Chinese journal of radio science,2017,32(4):410-415. (in Chinese).DOI: 10.13443/j.cjors.2017033001

O441.4

A

1005-0388(2017)04-0410-06

DOI10.13443/j.cjors.2017033001

2017-03-30

國家自然科學基金(No.61377080)

聯系人： 禹忠 E-mail: zhongyu@mail.xjtu.edu.cn