基于短時分數(shù)階傅里葉變換的譜分割算法

盧廣闊

(中國西南電子技術研究所,成都 610036)

基于短時分數(shù)階傅里葉變換的譜分割算法

盧廣闊

(中國西南電子技術研究所,成都 610036)

多分量非線性調頻信號在現(xiàn)代通信和雷達系統(tǒng)中應用越來越廣泛,而對其進行有效分析識別的常用算法就是短時分數(shù)階傅里葉變換(Short Time Fractional Fourier Transform, STFRFT)．文章首先討論了STFRFT的圓特性,證明了它基于高斯旋轉窗的非圓性并給出了修正的圓的STFRFT定義;在此基礎上研究了時頻變換后不同時頻點的譜峭度,進而推導出了區(qū)域集的譜峭度,并將該區(qū)域譜峭度作為譜圖上某區(qū)域內是否含有信號點的檢測因子;最后基于區(qū)域集譜峭度的區(qū)域增長算法被用于從譜圖中盲分割識別出各個非線性調頻分量信號．仿真實驗驗證了所提算法的有效性和魯棒性．

短時分數(shù)階傅里葉變換(STFRFT);非線性調頻信號;區(qū)域增長算法;譜峭度

引 言

非線性調頻(Nonlinear Frequency Modulation, NLFM)[1]信號指的是瞬時頻率隨時間非線性變化的一類非平穩(wěn)信號,它廣泛存在于現(xiàn)代雷達、語音、生電和地震物理等領域中．由于多個NLFM信號的分析識別技術具有重大的實用價值,國內外學者對此進行了大量的研究和探索．但該類信號的形式復雜多變,且常常被淹沒在噪聲之中,這使得對該類信號的分析識別首先需要將信號分量從噪聲中檢測出來,其次需要將多個NLFM信號分離開來．顯然,這是一個非常有難度的問題,因為現(xiàn)有的各類時頻分析方法在此類應用中常常存在這樣那樣的缺陷和不足[2]．短時分數(shù)階傅里葉變換(Short Time Fractional Fourier Transform, STFRFT)[3]是一種新提出的較為有效的時頻表示方法,它對于NLFM信號具有較好的時頻聚焦性,并對交叉項也具有較強的抑制作用．另外,基于短時傅里葉變換(Short Time Fourier Transform, STFT)的譜分割算法作為一種有效地從譜圖中自適應提取信號分量的新算法[4],已經成功地應用于自適應語音識別之中．在本文中,為了將STFRFT用于多分量NLFM信號的盲分析識別,本文擬將譜分割算法[5]引入其中,研究基于STFRFT的譜分割新算法．

本文的第一部分給出了將多分量NLFM信號建模成確定性信號分量的混合模型,并討論了為什么時頻變換要滿足圓特性．第二部分主要研究了STFRFT的變換特性,給出了高斯白噪聲和NLFM信號分量經過變換后的統(tǒng)計特性;為了更好地用于譜分割,我們給出了一個修正的圓的STFRFT,它使得變換后的所有復高斯噪聲變量都是圓的．第三部分進一步討論了修正STFRFT后噪聲點和含信號分量點的譜峭度差異,并推導出了區(qū)域譜峭度的表達式．最后給出了基于區(qū)域增長的STFRFT譜分割算法,并進行了仿真驗證．

1 信號模型

x(n) =s(n)+w(n)

n=0,1,…,N-1.

(1)

式中:s(n)為混合信號分量;l為各分量信號的對應序號;bl為各分量信號的幅度;ail(i=0,1,2,3)為第l個NLFM信號的相位系數(shù);N為采樣點數(shù)．

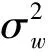
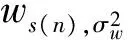
(2)

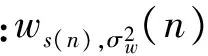
(3)

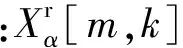
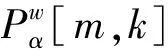
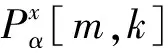
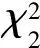
2 STFRFT的圓特性

作為分析NLFM信號的一種有效方法,STFRFT算法可以通過改變其窗函數(shù)的寬度和調頻斜率來提高時頻聚焦性．其基于時頻域的一般定義為[9]

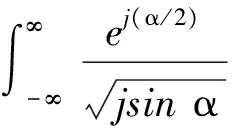
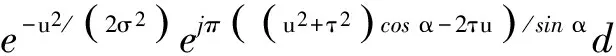
(4)

式中:u為分數(shù)階傅里葉域的索引;hα,σ(τ)為高斯旋轉窗函數(shù),該窗函數(shù)可以通過改變參數(shù)σ和α來分別控制窗的寬度和調頻斜率,進而改變STFRFT算法對時頻域多分量信號的分析識別性能．

顯然,選擇一個最優(yōu)的窗參數(shù)是該變換算法的核心,為此研究人員提出了各種選取準則．其中從時頻聯(lián)合分布的角度出發(fā),選擇最優(yōu)窗參數(shù)一般是基于最大時頻分辨率和最小時頻支撐兩種準則[6]．在理論分析中,由第一種準則可推出,當且僅當窗函數(shù)為高斯窗時,STFRFT具有最大時頻分辨率2/|sinα|;而考慮第二種準則,當信號具有最小時頻支撐時,可得窗函數(shù)[10]

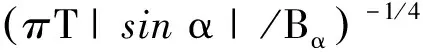
exp-Bαt2/(2T|sinα|)．

(5)

式中:T為時寬;Bα為信號在α階分數(shù)階傅里葉域的頻寬．

2.1旋轉高斯窗的譜密度

對離散時間序列x(n)進行M次STFRFT,則其時頻譜可以認為由M次復值傅里葉變換構成,取冗余點數(shù)為0,則表示為

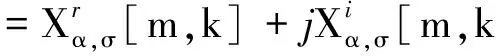
(6)

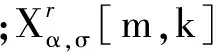
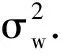
(7)

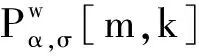
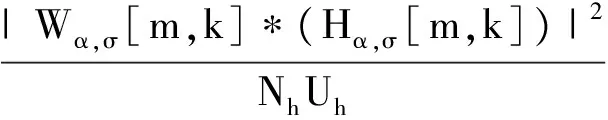
=wTγ[m,k]w

(8)

式中:0矩陣的大小可以調節(jié)與窗寬配對;C和S來自變換核的正弦和余弦,且有

Ω=diag(hα,σ(n))(Cm,k+Sm,k)i,j

(9)

向量w=[w0,w1,…,wNh-1]是由零均值高斯分布

函數(shù)構成的協(xié)方差矩陣向量;Wα,σ[m,k]和Hα,σ[m,k]分別表示噪聲信號w(n)和分析窗函數(shù)hα,σ(n)的離散傅里葉變換(Discrete Fourier Transform, DFT);*表示卷積．

對于高斯旋轉窗,定義γ[m,k]矩陣滿足

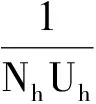
(10)

對γ[m,k]進行特征值分解,可得其非零特征值λα,σ滿足[8]

(11)

為了描述旋轉高斯窗的非零特征值隨時間和頻率的變化情況,進一步取λα,σ(γ[m,k])=max(λ1,λ2),并對其做仿真,仿真結果如圖1所示．其中,橫坐標為采樣點數(shù)m,縱坐標為頻點k,不同顏色表示不同時頻點的非零特征值λα,σ(γ[m,k]),其中深紅色表示值為1,白色表示值為0.5．

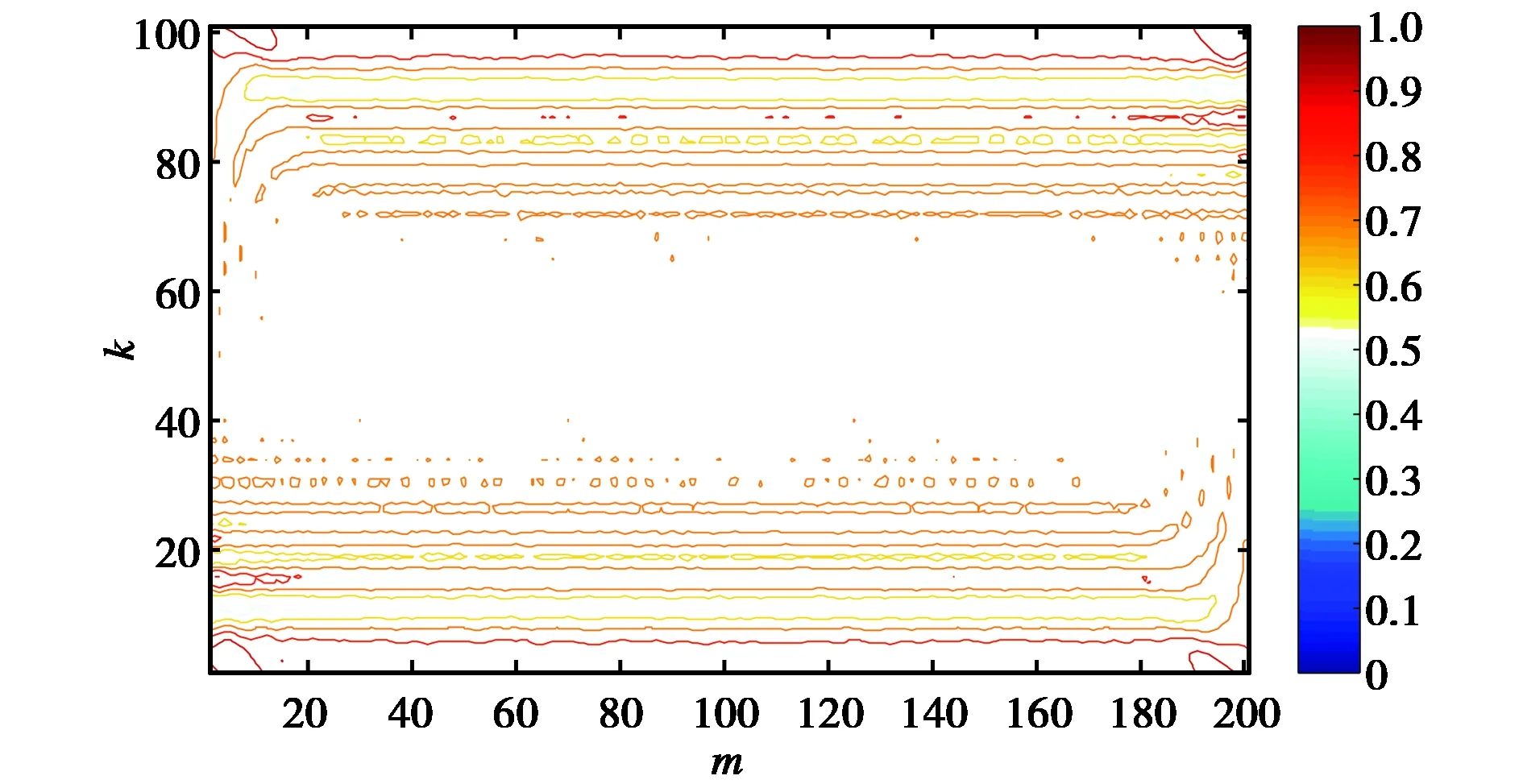
圖1 旋轉高斯窗的λα,σ[m,k]隨參數(shù) m和k的變化

從圖1可以看出:越是接近旋轉高斯窗頻域中間的點,其非零特征值越逼近0.5,則(λ1,λ2)越對稱;相反,越是遠離旋轉高斯窗頻域中心的點,其非零特征值越逼近1,則(λ1,λ2)越不對稱．

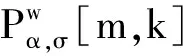
(12)

式中:U(·)表示均勻分布;I0為貝塞爾函數(shù)．

2.2基于旋轉高斯窗的STFRFT的非圓特性及修正

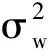
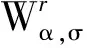
(cos(-2πkn/Nh))2;

綜上所述，我國城市化進程的不斷加快，極大地帶動了我國建筑行業(yè)的發(fā)展。為了緩解城市交通壓力，使我國地鐵工程大力發(fā)展，地鐵隧道工程施工也得到了越來越多人們的關注。本文通過對某市地鐵施工工程進行分析，從超前支護技術、二次襯砌技術、隧道開挖技術、初期支護技術4個方面對地鐵隧道施工技術進行了全面的分析，進而不斷提高我國地鐵隧道施工技術的應用水平，并且在此基礎上不斷創(chuàng)新，促進地鐵施工技術的發(fā)展。

(13)

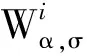
(sin(-2πkn/Nh))2.

(14)

式中,var(·)表示取方差．

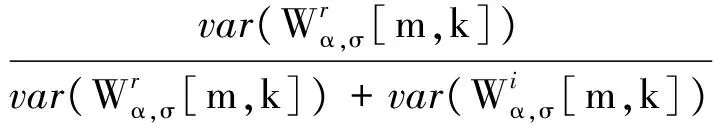
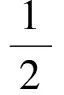
(15)

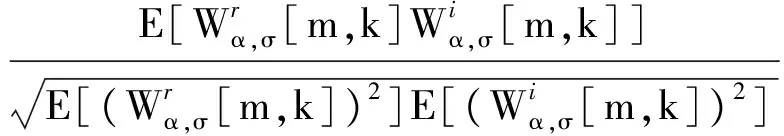
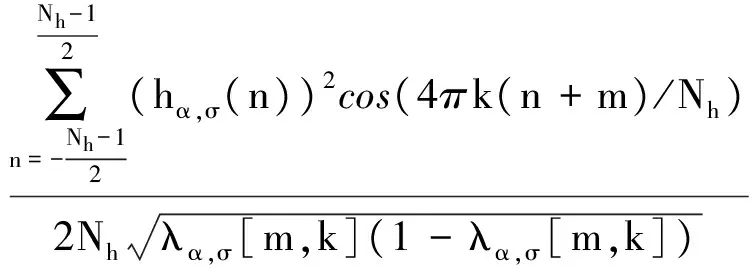
(16)

同樣的,上述兩式可以重寫成:

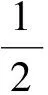
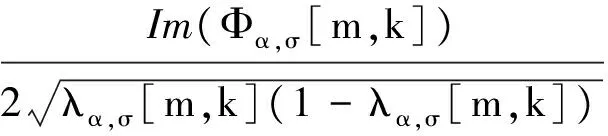
(17)

式中,函數(shù)Φα,σ[m,k]滿足

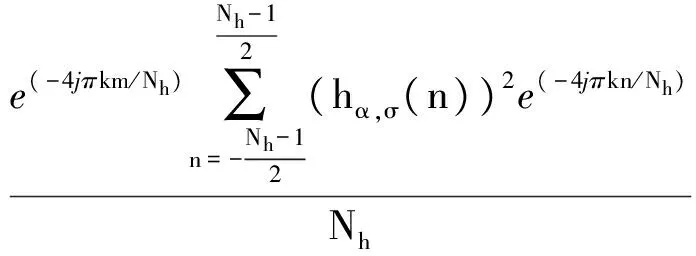
(18)

顯然,對于任何一個時頻點[m,k],當且僅當Φα,σ[m,k]等于0時,才有λα,σ[m,k]等于1/2,ρα,σ[m,k]等于0,此時才有離散STFRFT的系數(shù)Wα,σ[m,k]是圓的,這也就意味著基于高斯旋轉窗的STFRFT在該時頻點上是圓的．因此,討論函數(shù)Φα,σ[m,k]的性質非常有必要．

由式(18)可得,Φα,σ[m,k]由兩部分構成:相位系數(shù)e(-4jπkm/Nh)和離散窗函數(shù)平方(hα,σ(n))2的DFT．對于確定的m和k,相位系數(shù)的值是保持不變的,因此函數(shù)Φα,σ[m,k]的特性主要取決于離散窗函數(shù)的特性．而高斯旋轉窗的特性在2.1節(jié)中詳細討論過,不幸地是,其在大部分點上不滿足λα,σ[m,k]等于1/2．此時,即使有ρα,σ[m,k]等于0,函數(shù)Φα,σ[m,k]的實部也不等于0,則函數(shù)Φα,σ[m,k]也不為0．因此,基于旋轉高斯窗函數(shù)hα,σ(n)的STFRFT在大部分點上都是非圓的．

由第一節(jié)可知,當且僅當離散STFRFT是圓的時,零均值高斯白噪聲w(n)的功率譜系數(shù)才滿足中心χ2分布,含有信號能量的噪聲點的功率譜系數(shù)才滿足非中心χ2分布．因此,只有離散STFRFT滿足圓特性,這種不同時頻點的概率分布不同的特性才能被應用于分離信號和噪聲．為此,我們需要重新定義STFRFT如下[10]:

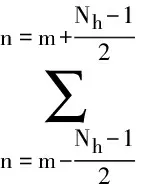
(19)

式中,hα,σ(n)為奇數(shù)窗．此時,Φα,σ[m,k]變?yōu)?/p>

Φα,σ[m,k] =Φα,σ[0,k]

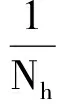
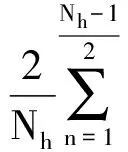
(20)

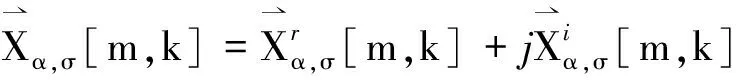
(21)

此時,當修正STFRFT取奇數(shù)窗時,在除邊緣點以外的所有點上都是圓的,因此有Φα,σ[m,k]等于0,對其做仿真,結果如圖2所示．不同顏色表示不同時頻點的Φα,σ[m,k]值,圖中深紅色表示值為1,白色表示值為0．由圖2可看出:除了邊緣點的值逼近1之外,其他點的值都逼近0,這證明了該修正定義的有效性和修正后STFRFT的圓性;邊緣點為1,是因為此處的噪聲為實高斯變量,不滿足圓性．

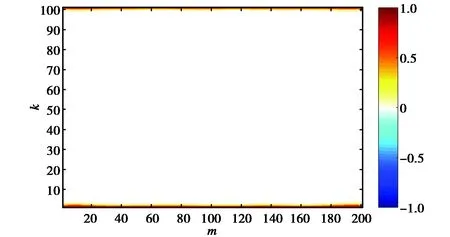
圖2 修正后Φα,σ[m,k]隨著參數(shù)m和k的變化

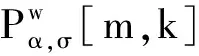
(22)

3 修正STFRFT的譜峭度

一般來說,時頻圖上的每個點都可以視為具有能量值的點,相鄰的點聚集起來可以視為某個信號的能量譜．而要想將需要的信號分量從噪聲或者其他分量信號中分離提取出來,只需要在時頻圖上將該信號分量的點區(qū)域分割出來,這就是時頻分割算法的用途．時頻分割就是通過分辨哪些點含有確定性信號分量、哪些點只含有噪聲來分割信號和噪聲區(qū)域的,甚至根據(jù)其他信息可以分割不同的信號分量．顯然,要想有效分割噪聲和信號以及信號和信號,只有能量值信息是遠遠不夠的,這是因為

1) Heisenberg-Gabor不等式使得信號在時頻點的能量值受到該點鄰域的影響,因此該點的時頻變換系數(shù)無法完全描述信號在該點的所有信息;

2) 信號的功率譜是隨機嵌入噪聲功率的,這使得該點的能量值具有隨機因素．

綜上所述,需要考慮使用其它的統(tǒng)計特征量來代替能量值作為時頻分割的檢測因子．另外,考慮到時頻表示不確定原理,一個點的譜系數(shù)無法完全表示該點的全部信息,因此需要考慮一組點的譜系數(shù),也就是說需要考慮一個包含點數(shù)目相對較小卻能描述某個時頻點所有信息的區(qū)域集．研究該區(qū)域的統(tǒng)計特征來作為新的區(qū)分噪聲或者加噪信號的標準,從而將信號分量從周圍噪聲中以及其他信號分量中分離出來．這就是本文的研究思路,而在本文中,選取的統(tǒng)計特征就是區(qū)域集的譜峭度．

由2.2節(jié)可得

ρα,σ[m,k]=0.

(23)

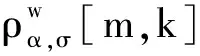
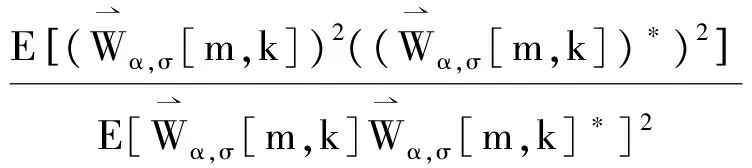
(24)

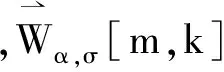
(25)

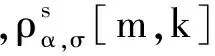
進一步的,選取一個擁有Nh個點的區(qū)域,并假定該區(qū)域內里有Uα點含有信號的能量,其他點為噪聲點,那么有

(26)

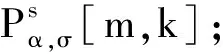
(27)

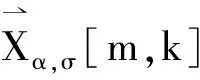
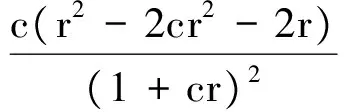
(28)

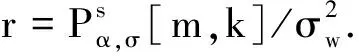
4 基于STFRFT譜的譜分割算法

4.1算法原理

多個NLFM信號的分析識別主要分為兩部分,首先運用第二節(jié)所提修正STFRFT算法將混合信號變換到時頻域,然后運用基于區(qū)域譜峭度的譜分割算法將所含噪信號點和噪聲點一一分離,最終提取出想要的分量信號,其算法流程具體如下[3]:

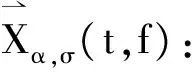
Nh=6σfs,

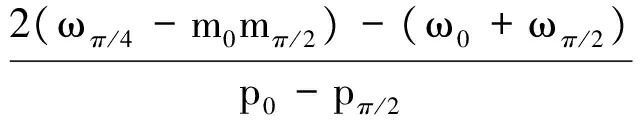
(29)

式中,mα、ωα和pα分別表示旋轉α后的一階矩、二階

矩和二階中心矩．

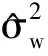
(30)

式中,MK為含有信號能量的點數(shù)．然后,給定噪聲方差的較大估計值并將觀測信號的STFRFT譜分割成H0和H1兩部分．其中H1部分對應二階統(tǒng)計量大于給定門限值的時頻區(qū)域,其余部分為H0．在初次迭代中,H0部分中大部分點為噪聲點,但有部分點含有信號成分．再次給定較小的噪聲方差估計值,對H0部分進行二次分割．隨著迭代進行,給定的噪聲方差估計值越來越小,越來越逼近真正的噪聲方差．

3) 由第三節(jié)可得,時頻圖中混合區(qū)域的譜峭度為正,噪聲區(qū)域的譜峭度為0,因此可用譜峭度作為時頻分割算法的迭代終止準則．此時,選取區(qū)域譜峭度的二次標準偏差為門限值[4]:

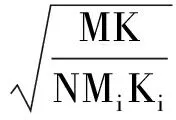
(31)

式中,MiKi為第i次迭代時噪聲的點數(shù)．當H0部分的譜峭度小于門限值tFRFSK時迭代停止,此時可以認為剩余點只有復圓高斯分布的噪聲了,而相對的H1部分可以認為只剩下信號分量了．

4) 最后,對H1部分應用圖像分割算法[14]中的區(qū)域增長算法[15]．首先選取H1部分中二階統(tǒng)計量最大的點作為種子,搜索其周圍8-鄰域的相似點,當所有相似點搜索完畢后將其標記為 label 1;然后再設置另一個種子,繼續(xù)搜索標記為label 2,最后將時頻圖內所有的信號分量一一進行識別標記．

4.2仿真實驗

為驗證所提算法,選取多個NLFM信號組成的多分量信號疊加高斯白噪聲作為混合信號,其中加性高斯白噪聲w(n)的均值為0、方差為1,信噪比為0 dB．顯然,NLFM多分量信號形式非常復雜,需要時頻聚焦性較高的時頻變換算法才能分辨．下面分別用STFT、魏格納-威廉分布(Wigner-Ville Distribution, WVD)、改進B分布以及本章所提STFRFT算法對其進行時頻分析,仿真結果如圖3所示．

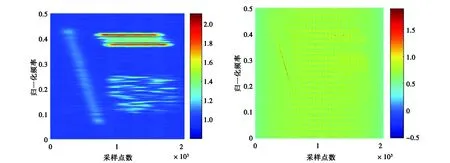
(a) STFT (b) WVD

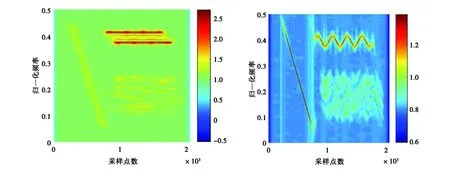
(c) 改進B分布 (d) STFRFT圖3 多個NLFM信號分量的時頻圖

從圖3可以看出:STFT算法雖然沒有受到交叉項的影響,但對信號的聚焦性一般;而WVD算法可以達到時頻聚焦性的下限,但它產生了大量的自交叉項和互交叉項且對噪聲極為敏感;作為保留時頻聚焦性的同時去除噪聲和交叉項的一個折衷算法,改進B分布是目前核函數(shù)類時頻分析方法中最好的變換,但是仍然比不上STFRFT算法的聚焦性,因此這證明了本文所提算法時頻聚焦性優(yōu)于其它算法．

在對多分量混合信號進行STFRFT后,得到了該混合信號的時頻圖．接著,運用基于區(qū)域譜峭度的譜分割算法來提取時頻圖中的信號分量,并用不同的顏色分別進行標記．具體步驟見4.1節(jié),仿真結果如圖4所示,三個不同的信號分量被成功提出,并且用不同顏色一一標記．其中,大部分噪聲被濾除,且估計噪聲方差為1.004;當?shù)K止時,H0部分的譜峭度為0.042,而門限值為0.045．

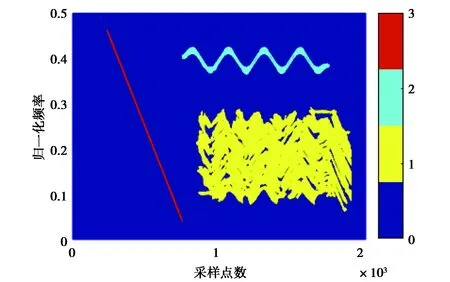
圖4 多個NLFM信號分量的STFRFT譜分割結果

接著,為了比較所提算法在多種信噪比情況下性能,對NLFM分量信號的瞬時頻率進行估計,取其均方誤差(Mean Squared Error, MSE)為評判標準,仿真結果如圖5所示.顯然所提算法的仿真性能優(yōu)于其他算法,且在低至-5 dB信噪比(Signal-to-Noise Ratio, SNR)下仍然有效．

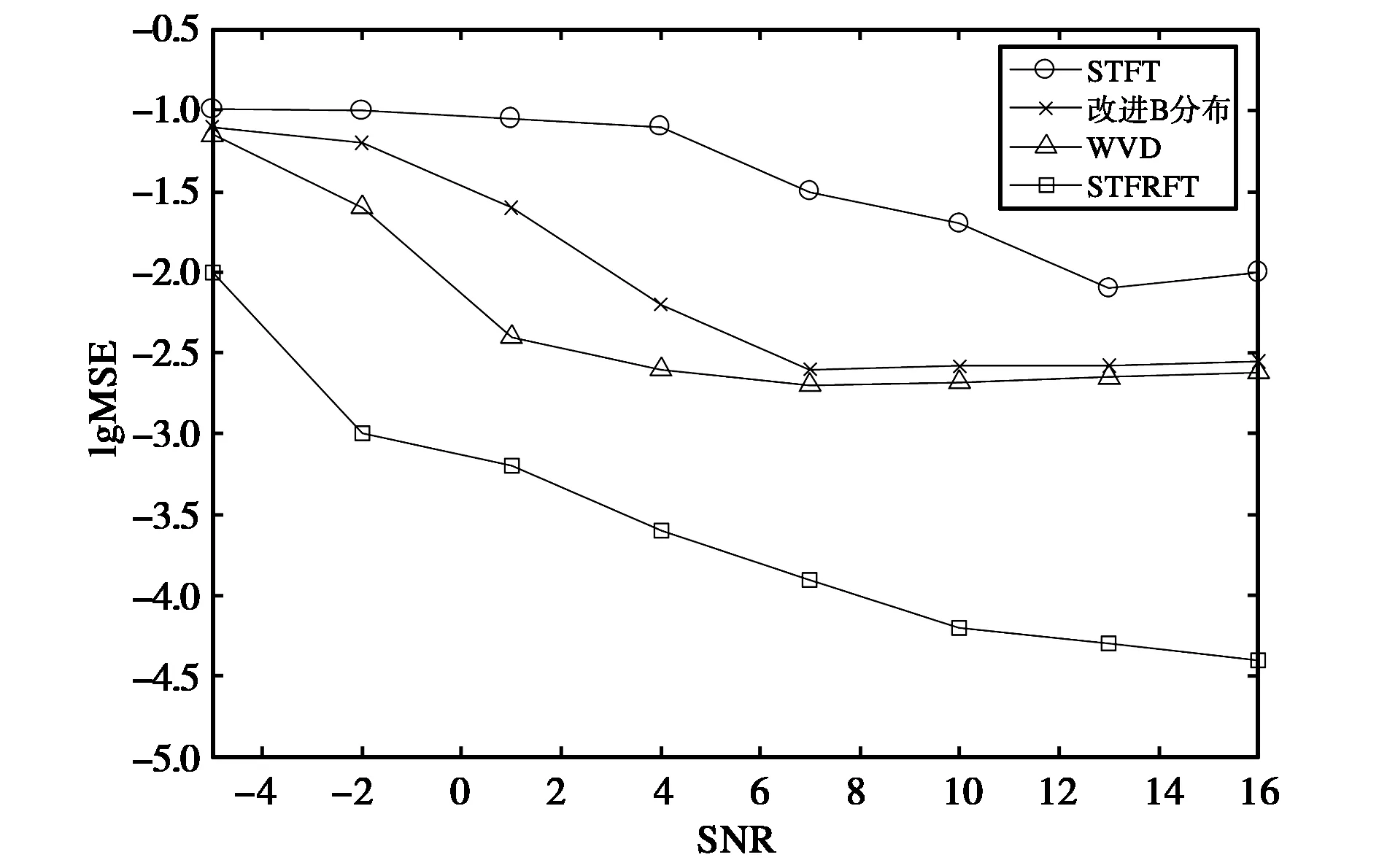
圖5 NLFM信號分量的瞬時頻率估計MSE值

5 結 論

本文提出了一種基于STFRFT和譜峭度的譜分割新算法,并將其成功用于多個NLFM信號的檢測和識別中．本文首先研究了高斯白噪聲的離散STFRFT的功率譜概率密度和非圓性,給出了一種滿足圓性的修正STFRFT算法;接著,研究了變換后噪聲點和信號點的譜峭度差異,并推導出了區(qū)域譜峭度的公式;然后區(qū)域譜峭度被用于譜分割迭代算法的終止準則,并通過區(qū)域增長算法成功地提取混合信號中所需的信號分量．最后,仿真驗證了本文所提算法的有效性和自適應性．

另外,本文算法盡管提高了NLFM信號的盲識別性能,但同時也增加了算法的復雜度,畢竟非線性、自適應性以及更好估計性能都需要更大的計算成本．尤其是隨著NLFM信號數(shù)量的增加,H1部分的點數(shù)會增加,后續(xù)圖像分割算法的迭代次數(shù)也會增加,最終會增加整個算法的計算復雜度．而在提高算法性能的同時降低算法的復雜度是本文進一步的研究方向．

[1] 張賢達, 保錚. 非平穩(wěn)信號分析與處理[M].北京:國防工業(yè)出版社, 1998: 70-71.

[2] 王璞, 楊建宇. 基于乘積性模糊函數(shù)的核函數(shù)設計方法[J]. 電波科學學報, 2007, 22(6): 1056-1067.

WANG P, YANG J Y. Kernel design for quadratic time-frequency distribution using product ambiguity function[J]. Chinese journal of radio science, 2007, 22(6): 1056-1067. (in Chinese)

[3] PELEG S, POART B. The Cramer-Rao lower bound for signals with constant amplitude and polynomial phase[J]. IEEE transactions on signal processing, 1991, 39(3): 749-752.

[4] MILLIOZ F, MARTIN N. Circularity of the STFT and spectral kurtosis for time-frequency segmentation in Gaussian environment[J]. IEEE transactions on signal processing, 2011, 59(2): 515-524.

[5] HORY C, MARTIN N, CHEHIKIAN A. Spectrogram segmentation by means of statistical features for non-stationary signal interpretation[J]. IEEE transactions on signal processing, 2002, 50(12): 2915-2925.

[6] 靖晟, 劉渝, 席軼敏, 等. 非線性調頻信號參數(shù)估計算法[J]. 南京航空航天大學學報, 2001, 33(5):441-444.

JING S, LIU Y, XI Y M, et al. Parameters estimation of nonlinear FM signals[J]. Journal of Nanjing University of Aeronautics &Astronautic, 2001, 33(5):441-444.(in Chinese)

[7] KOOPMANS H L. The spectral analysis of time series[M]//Probability & mathematical statistics. New York: academic press, 1995: 354-358.

[8] JOHNSON P E, LONG D G. The probability density of spectral estimates based on modified periodogram averages[J]. IEEE transactions on signal processing, 1999, 47(5): 1255-1261.

[9] OUYANG X, AMIN M G. Short-time Fourier transform receiver for nonstationary interference excision in direct sequence spread spectrum communications[J]. IEEE transactions on signal processing, 2001, 49(4): 851-863.

[10] TAO R, LI Y L, WANG Y. Short-time fractional

Fourier transform and its applications[J]. IEEE transactions on signal processing, 2010, 58(5): 2568-2580.

[11] LU G K, WEI P. Circularity of the fractional Fourier transform and spectrum kurtosis for LFM signal detection in Gaussian noise model[J]. IEICE transactions on fundamentals of electronics, communications and computer sciences, 2015, 98(12): 2709-2712.

[12] LU G K, XIAO M L, WEI P. Adaptive short time fractional Fourier transform for time-frequency segmentation[J]. Electronics letters, 2016, 52(8): 615-617

[13] ZHANG X, PENG Z, ZHANG P, et al. Spectral decomposition of seismic signal based on fractional Wigner-Ville distribution[J]. Oil geophysical prospecting, 2014, 49(5): 839-846.

[14] 楊帆, 楊健, 殷君君.基于區(qū)域譜聚類的極化合成孔徑雷達圖像分割[J].電波科學學報, 2015, 30(1): 37-42.

YANG F, YANG J, YIN J J. Polarimetric SAR segmentation based on region merging and spectral clustering[J]. Chinese journal of radio science, 2015, 30(1): 37-42. (in Chinese)

[15] ADAMS R, BISCOF L. Seeded region growing[J]. IEEE transactions on pattern analysis and machine intelligence, 1994, 16(6): 641-647.

盧廣闊(1983—),男,河北人,2016年獲電子科技大學信號與信息處理博士學位,主要研究方向為通信信號偵察、多分量信號分析識別等．

AnewspectralsegmentationalgorithmbasedonshorttimefractionalFouriertransform

LUGuangkuo

(SouthwestChinaInstituteofElectronicTechnology,Chengdu610036,China)

The short time fractional Fourier transform (STFRFT) is a useful tool for the research on analysis and recognition of multi-component non-linear frequency modulation (NLFM) signals, which have been presented on a lot of communication systems and radar systems. This paper investigates the non-circularity of STFRFT coefficients, and proposes a modified STFRFT such that all coefficients coming from white Gaussian noise are circular. In order to use the spectral kurtosis (SK) as a Gaussian test to check if signal points are present in a set of STFRFT points, we study the SK of different points in the time-frequency transform figure, and propose the definition of the local SK. Finally, a time-frequency segmentation algorithm based on the region growing by the local SK is proposed to separate the multi-component NLFM signals. The effectiveness and robustness of this algorithm are evaluated via simulations.

short time fractional Fourier transform; non-linear frequency modulation signals; region growing algorithm; spectral kurtosis

盧廣闊. 基于短時分數(shù)階傅里葉變換的譜分割算法[J]．電波科學學報,2017,32(4):474-481.

10.13443/j.cjors.2017030702

LU G K. A new spectral segmentation algorithm based on short time fractional Fourier transform [J]. Chinese journal of radio science,2017,32(4):474-481. (in Chinese). DOI: 10.13443/j.cjors.2017030702

TN958.93

A

1005-0388(2017)04-0474-08

DOI10.13443/j.cjors.2017030702

2017-03-07

聯(lián)系人： 盧廣闊 E-mail: guangkuolu@gmail.com