短波時差定位中電離層參數對定位影響仿真

攸陽 錢志剛 李吉寧 柳文

(1.海軍參謀部信息通信局,北京 100841;2.中國電波傳播研究所,青島266107)

短波時差定位中電離層參數對定位影響仿真

攸陽1錢志剛2李吉寧2柳文2

(1.海軍參謀部信息通信局,北京 100841;2.中國電波傳播研究所,青島266107)

在短波波段,由于電離層反射傳播,電波傳播路徑與實際地面距離存在較大差異,傳統時差定位方法不再適用．文章提出一種基于電離層射線追蹤技術的時差定位技術,在此基礎上,仿真分析了電離層參數對定位精度的影響．結果表明:在準確獲取電離層信息情況下,本方法可準確定位目標;電離層測量誤差對定位精度影響較大;站點增加可提高定位精度,降低對電離層參數獲取精度要求．仿真結果為短波時差定位系統研制以及電離層參數獲取精度要求提供了理論依據．

時差定位;射線追蹤;電離層模型;定位誤差

引 言

短波偵測定位是遠距離大范圍偵察監視目標定位重要的手段之一,同時,由于采用被動偵察技術,具有“反隱”的天然優勢,不易被偵察對象察覺,能極大提升其戰場生存能力．

短波偵測定位主要包括測向交匯定位、單站定位和時差定位．短波測向交匯定位技術利用大型陣列天線獲得來波方向,利用多站測向結果,交匯確定目標位置[1];短波單站定位技術利用陣列天線獲得來波方向和仰角信息,結合電離層反射高度信息確定目標位置[2];時差定位(Time Difference of Arrival, TDOA)技術不依賴陣列天線,只分析輻射信號到達各偵收站的時間差異,即可實現被動定位[3],與測向交匯定位和單站定位相比,具有設備規模小、費用低等優勢,可充分利用當前分布廣泛的偵收站拓展其工作效能,有效彌補現役偵察系統的業務“盲區”．

常規時差定位是通過測量移動臺(目標位置)發射信號到達多個基站的距離差,確定目標位置．例如測得目標到達基站Bi和基站Bi+1的距離差,則目標定位方程為[3]:

=rr+1,i.

(1)

由式(1)可以看出,目標位于以Bi和Bi+1為焦點的雙曲線上,若同時測得到達三個站(或以上)的距離差,則可以確定目標位置．常規時差定位的關鍵是求解非線性雙曲線方程組,主要包括Chan算法[4-5]和Taylor展開法[6-7]等．

常規的時差定位方法主要適用于視距傳播,對于短波超視距傳播,受電離層折射傳播影響,無法準確獲取真實的地面距離差．因此,若以電波傳播距離作為地面距離進行時差定位處理,常規時差定位方法會出現較大的定位誤差．

文獻[8]提出了一種基于電離層反射的短波信號時差定位方法．該方法假定在目標點附近有一個已知位置的電臺,通過測量定位站與電臺時差,推算電臺到每個定位站的電離層高度,并將該電離層高度作為目標點到定位站的電離層高度的近似值．然而在實際工程中,電臺是定頻工作,該方法只能計算單一工作頻率下的電離層高度,而不同頻率電離層反射高度不同,因此該方法在實際應用中存在一定的局限性．

針對短波時差定位,本文在文獻[8]基礎上提出了一種新的短波時差定位方法,該方法不受頻率限制．最后仿真分析了電離層參數對時差定位精度的影響．

1 基于射線追蹤的時差定位方法

1.1定位原理

定位采用搜索方法,首先確定目標的大概位置,以該位置為中心,在一定的搜索半徑內,按照一定的距離間隔將區域劃分為若干網格,依次假設目標位于各網格點內,采用遍歷方法,利用射線追蹤技術,計算網格點到各站的電波傳播距離,計算各路徑時差,將時差與實際時差最接近的網格點確定為目標位置．

其中,射線追蹤所需大區域電離層參數可在多站點實時探測(如電離層垂測儀、斜向探測儀和返回散射探測儀等)基礎上,經反演、差值、重構獲得．

1.2電離層射線追蹤技術

射線追蹤技術作為電波傳播研究與應用的基本工具之一,通常分為兩類:解析射線追蹤[9-10]和數值射線追蹤[11]．解析射線追蹤通常是忽略地磁場和碰撞影響,并且假設電離層球形對稱分布,基于特定的電離層模型獲得射線傳播路徑參數的解析表達式．用于實現解析射線追蹤的模型有準拋物[9]或分段準拋物[10]等．當電離層非均勻或者考慮地磁場和碰撞影響時,射線傳播路徑參數的解析表達式無法獲得,需用數值方法進行求解,該方法雖然也能獲得比較準確的結果,但計算量較大．本文采用解析射線追蹤進行仿真．

解析射線追蹤通常忽略地磁場和碰撞影響,并且假設電離層球形對稱分布,基于準拋物電離層模型獲得的射線傳播地面距離D、群路徑P′、相位路徑Pr解析表達式為[9]:

D=r0(βb-β0)+

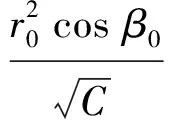
(2)

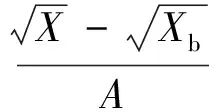
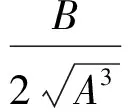
(3)

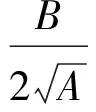
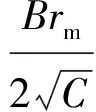
(4)

式中:A=1-(fc/f)2+(fcrb/(fym))2;

B=-2rm(fcrb/(fym))2;

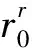
X=Ar2+Br+C;

βb=cos-1((r0/rb)cosβ0),r0為地球半徑,rb為電離層底高,β0為電波射線仰角;f為工作頻率;fc為臨界頻率;ym為層的半厚;rm為最大電子密度的高度(簡稱峰高),rm=rb+ym．

電離層射線追蹤詳細實現方式可參考文獻[9-11]．

電離層電子密度分布采用準拋物模型,該模型與實際分布相當接近,其數學表達式比較簡單,方便求得解析解,其表達式為[12]

(5)

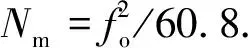
2 仿真分析

2.1三站定位仿真

本文主要分析電離層參數對定位影響,為方便分析,做以下假設:

1) 準確獲取時差信息,不考慮時差提取誤差;

2) 假設電離層均勻且所有反射點電離層狀態相同;

3) 電離層為單F層．

對于三站定位,假設三個站坐標分別為B0(0,0)、B1(800,0)和B2(0,-500),目標位于M(0,800)點處,目標到三個站的地面距離分別為900 km、1 204.2 km和1 700 km．電離參數為:臨界頻率為15 MHz,底高為200 km,峰高為300 km,工作頻率為15 MHz．

根據目標到B0、B1和B2三個站的地面距離D,利用射線追蹤,可計算獲得相應的射線路徑分別為933.1 km、1 229.2 km和1 388.9 km．因此,可得站B0與站B1和B2的射線路徑差P10、P20分別為296.1 km和455.7 km,下文以此路徑差為基礎進行仿真分析．

在準確獲取電離層參數情況下,采用1.1節定位方法對目標進行定位,在目標位置周圍400 km內以間距5 km劃分網格,依次求解各網格點到三個站的射線路徑,然后計算相應的時差,選擇計算時差與實際時差差值最小的網格點為目標位置．仿真結果表明,在電離層參數準確獲取情況下,本文提出的方法可以準確定位目標,如圖1所示．

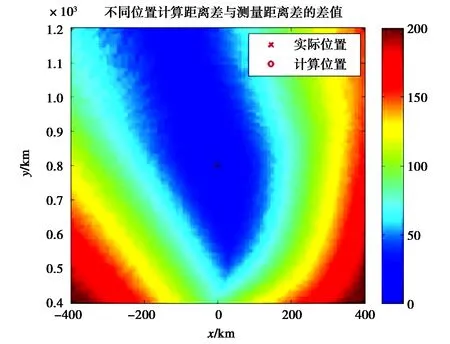
圖1 準確獲取電離層參數時定位結果

2.2電離層參數誤差對定位影響分析

1) 臨界頻率誤差對目標定位影響

保持其他參數不變,改變臨界頻率,分析臨界頻率測量出現誤差時,對定位影響．圖2給出了不同臨界頻率下的定位誤差．從圖2中可以看出,當臨界頻率大于10 MHz或大于20 MHz時,定位誤差較大,最大超過400 km．

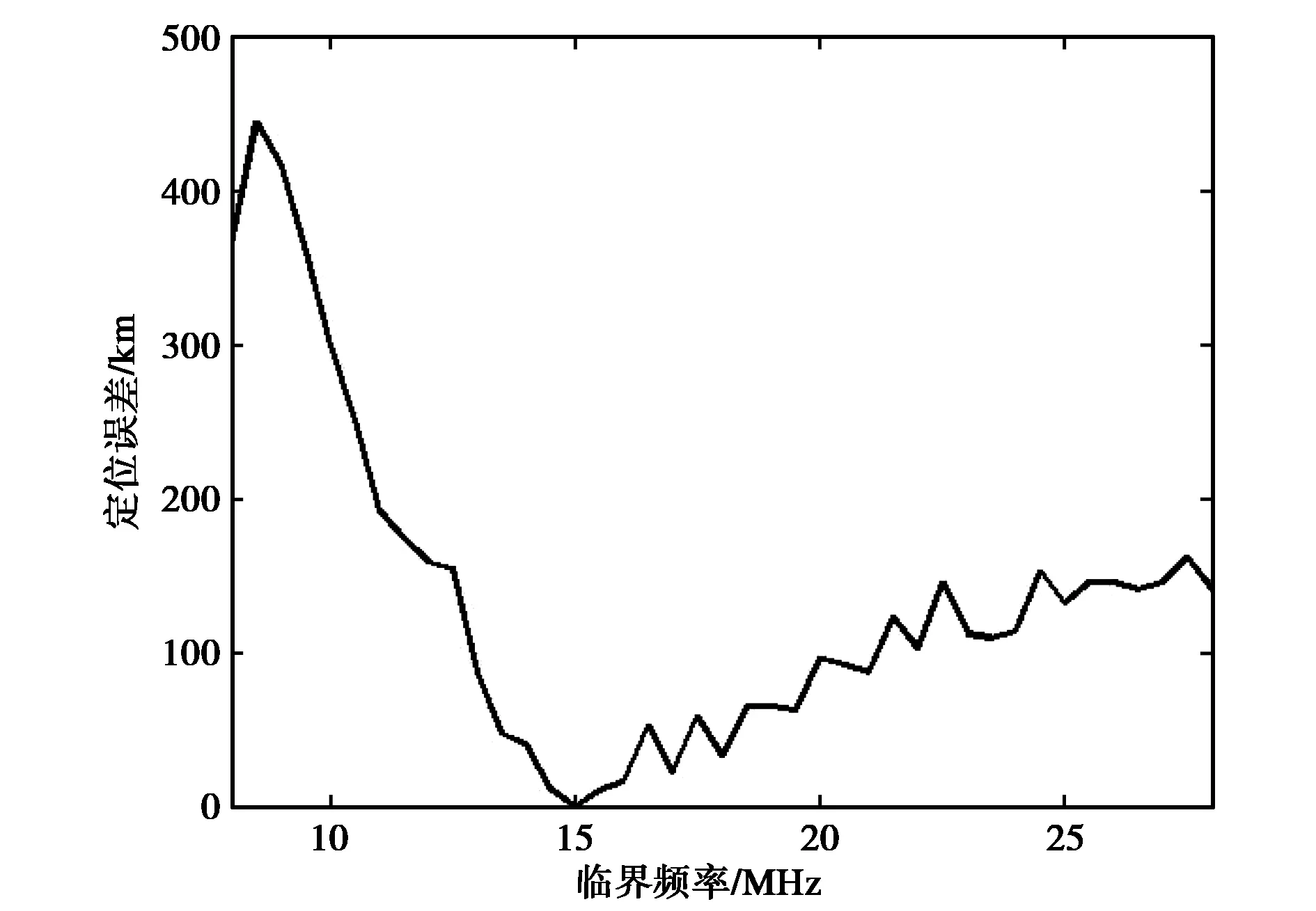
圖2 不同臨界頻率時的定位誤差 (實際臨界頻率為15 MHz)

2) 底高誤差對目標定位影響

保持其他參數不變,改變底高,獲得不同底高情況下的定位誤差,如圖3所示．從圖中可以看出當底高在150～250 km時,時差定位誤差基本在100 km以內．

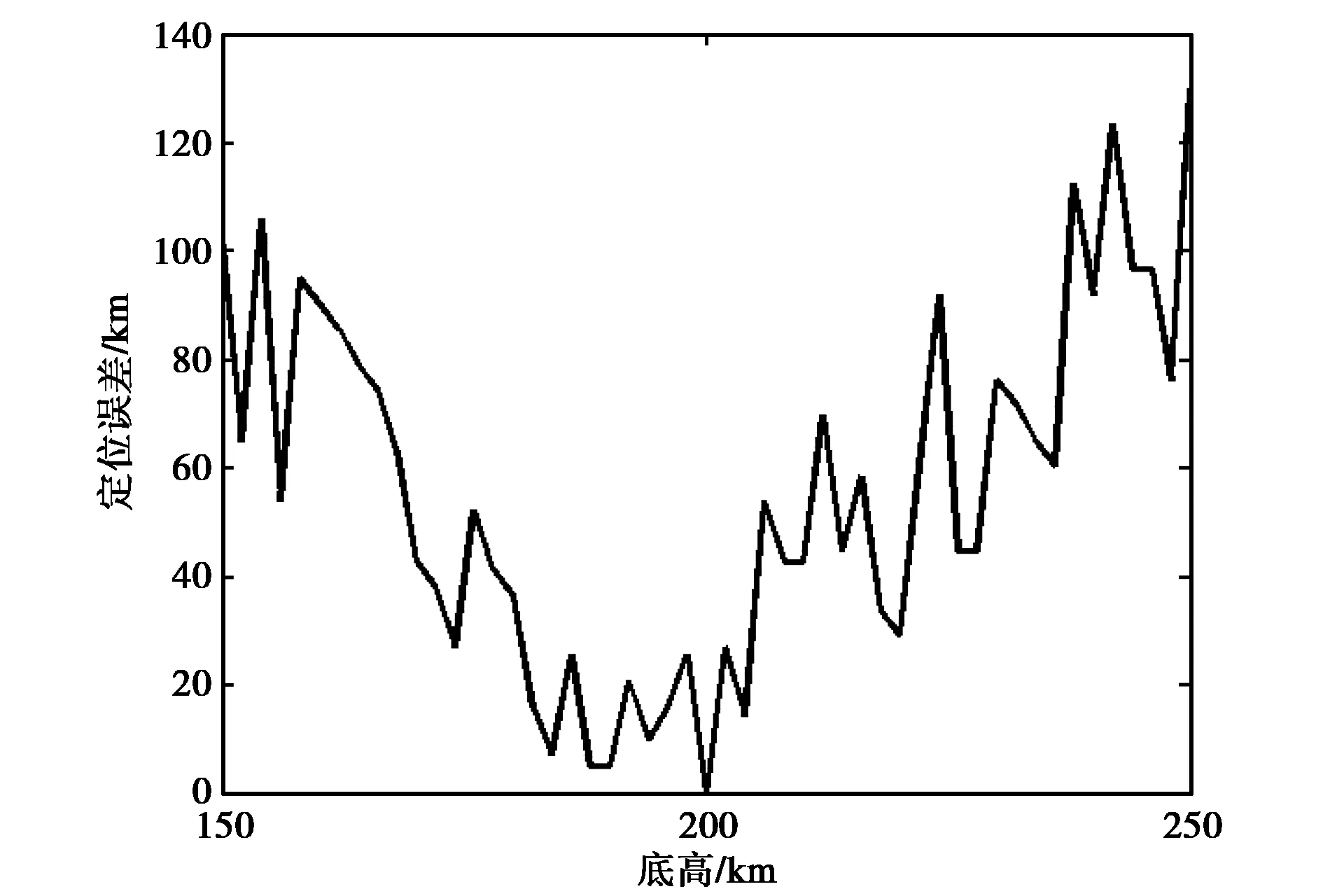
圖3 不同底高時的定位誤差

3) 峰高誤差對目標定位影響

保持其他參數不變,改變峰高參數,獲得不同情況下的定位誤差,如圖4所示．從圖中可以看出當峰高在250～350 km時,定位精度基本在100 km以內．

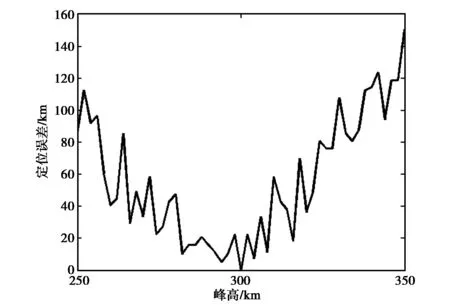
圖4 不同峰高的定位誤差

2.3四站定位仿真

為進一步分析站點增加對定位影響,仿真分析了四站情況下定位誤差．

增加一個觀測站(800,0),保持其他仿真參數不變,分別改變臨頻、底高、峰高等電離層參數,仿真不同參數下定位誤差,結果如圖5所示．

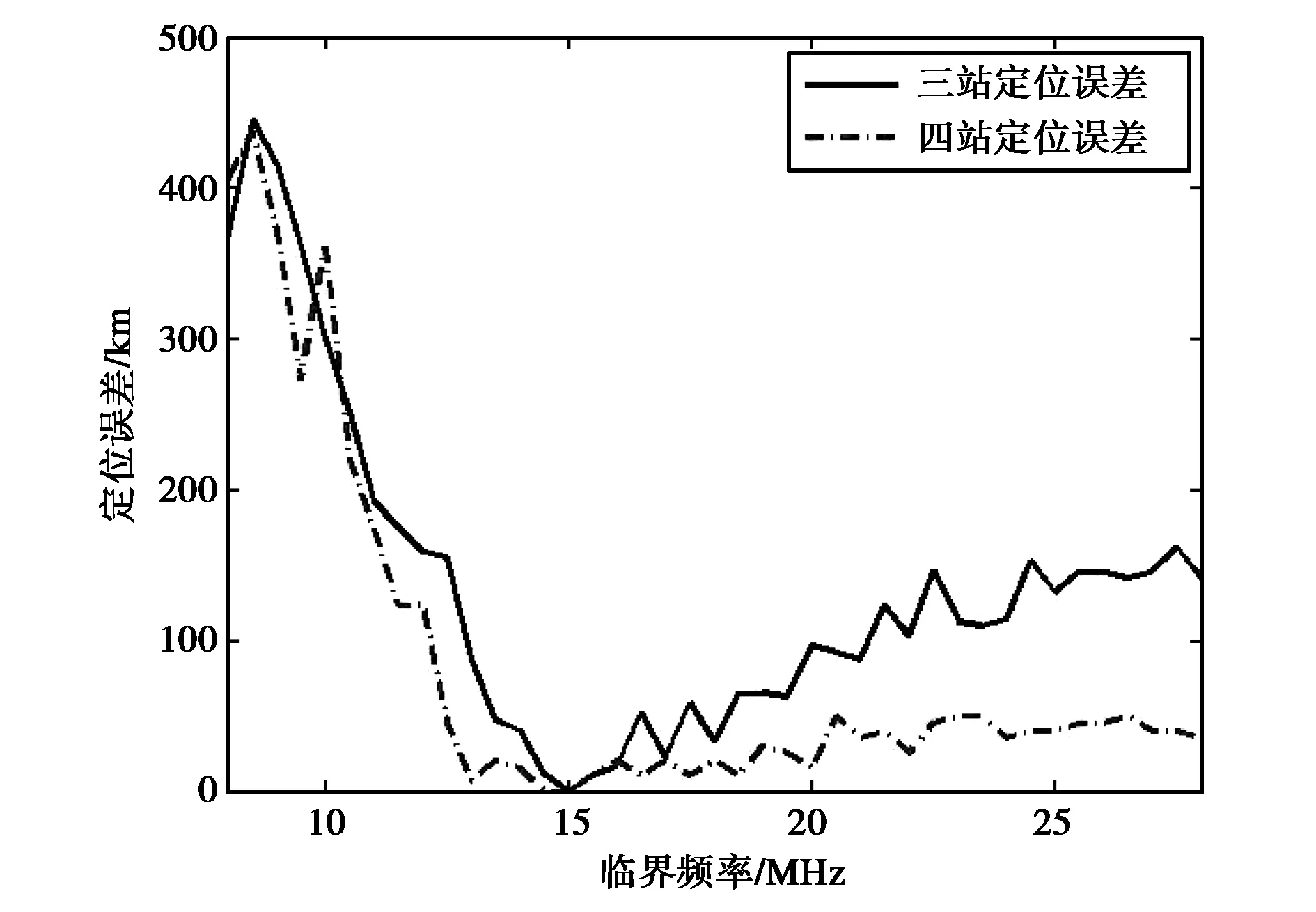
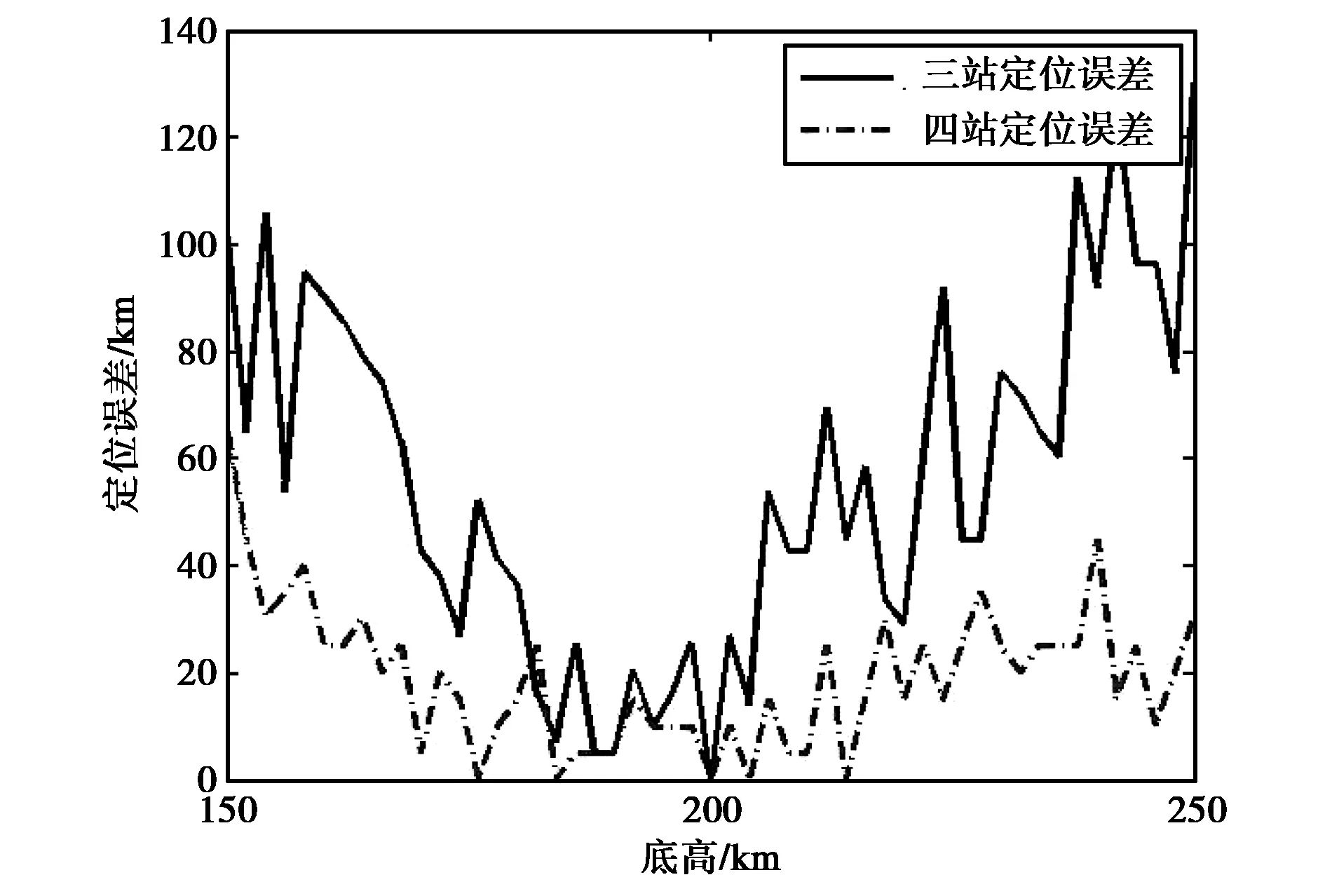
圖5 三站與四站電離層參數變化對比圖

從圖5可以看出,與三站定位相比,相同電離層測量參數下,四站定位精度更高,對電離層參數的獲取準確度要求更低．

2.4多層定位分析

以上給出了電離層僅存在F層時的仿真結果,而實際電離層通常由多個層構成,在四站定位下,對存在F1層和F2層電離層情況進行仿真．在保持其他參數不變情況下,分別更改各層臨頻、底高和峰高,結果表明:F1層電離層參數(包括臨頻、底高和峰高)誤差對定位誤差影響較F2層影響更大;其中F1層臨頻影響最大,誤差4 MHz造成定位誤差可達400 km以上．

3 結 論

本文提出了一種基于電離層射線追蹤的時差定位方法,在此基礎上,研究了電離層參數對定位誤差的影響,結果表明:

1) 在準確獲取電離層信息情況下,本方法可準確定位目標;

2) 電離層測量誤差對定位精度影響較大;

3) 站點增加對于提高定位精度具有重要意義,可降低對電離層參數獲取精度要求．

本文重點仿真了理想均勻電離層條件下短波時差定位方法,以及電離層參數對定位誤差影響,由于電離層的復雜性,非均勻電離層情況下時差定位有待進一步分析;同時上述結論也有待進一步試驗驗證．

[1] 張洪順, 王磊. 無線電監測與測向定化[M]. 西安:西安電子科技大學出版社, 2011.

[2] 馮曉哲, 黃昌理.短波單站定位中大圓距離的確定[J]. 通信對抗, 2008, 100(1): 42-45.

FENG X Z, HUANG C L. Range estimation for single station location HFDF systems[J]. Communication countermeasures, 2008, 100(1): 42-45.(in Chinese)

[3] 王永誠,張令坤. 多站時差定位技術研究[J]. 現代雷達,2003, 25(2): 1-4.

WANG Y C, ZHANG L K. Position location using TDOA measurements in multi-sites[J]. Modern radar, 2003, 25(2): 1-4.(in Chinese)

[4] CHAN Y T, HO K C. A simple and efficient estimator for hyperbolic location[J]. IEEE transactions on signal processing, 1994, 42(8): 1905-1915.

[5] 李招華, 汪毓鐸, 邵青. 基于Chan的TDOA三維定位算法[J]. 現代電信科技, 2014, 44(11): 36-40.

LI Z H, WANG Y D, SHAO Q. A3-dimension localization algorithm based on TDOA using Chan[J]. Modern science & technology of telecommunications, 2014, 44(11): 36-40.(in Chinese)

[6] 李莉, 鄧平, 劉林. 基于泰勒級數展開的蜂窩TDOA定位算法[J]. 現代電信科技, 2002, 37(6): 684-688.

LI L, DENG P, LIU L. Taylor series expansion method and its performance analysis[J]. Journal of Southwest Jiaotong University, 2002, 37(6): 684-688.(in Chinese)

[7] 張令文, 談振輝. 基于泰勒級數展開的蜂窩TDOA定位新算法[J]. 通訊學報, 2007, 28(6): 7-11.

ZHANG L W,TAN Z H. New TDOA algorithm based on Taylor series expansion in cellular networks[J]. Journal on communications, 2007, 28(6): 7-11.(in Chinese)

[8] 何青益, 高京晉. 短波信號電離層反射時差定位可行性分析[J]. 電子對抗, 2011,141 (6): 25-27.

[9] CROFT T A, HARRY H. Exact ray calculations in a quasi-parabolic ionosphere with no magnetic field[J]. Radio science, 1968, 3(1): 69-74.

[10] DYSON P L, BENNETT J A. A model of the vertical distribution of the electron concentration in the ionosphere and its application to oblique propagation studies[J]. Journal of atmospheric and terrestrial physics, 1988, 50(3): 251-262.

[11] JONES R M. A three dimensional ray tracing computer program[J]. Radio science, 1968, 3(1): 93-94.

[12] KOHNLEIN W. Electron density models of the ionosphere[J]. Reviews of geophysics, 1978, 16(3): 341-354.

攸陽(1978—),男,河北人,碩士,海軍參謀部信息通信局工程師,主要研究方向為無線通信.

錢志剛(1991—),男,山東人,碩士,中國電波傳播研究所工程師,主要研究方向為信號處理.

李吉寧(1982—),男,山東人,碩士,中國電波傳播研究所高級工程師,主要研究方向為高頻雷達、電離層電波傳播、信號處理等.

柳文(1973—),男,湖南人,博士,研究員級高工,主要研究方向為電離層物理及電波傳播等.

SimulationontheeffectofionosphericparametersonTDOAlocationinshortwave

YOUYang1QIANZhigang2LIJining2LIUWen2

(1.InformationandCommunicationBureauoftheChineseNavyStaff,Beijing100841,China;2.ChinaResearchInstituteofRadiowavePropagation,Qingdao266107,China)

In the short wave band, traditional time difference of arrival(TDOA) location method is no longer applicable for the big difference between the radio path and the actual ground distance brought on by the ionospheric reflection propagation. A new TDOA location method based on ray tracing technique is proposed, and the influence of ionospheric parameters on location precision is analyzed. The results show that in obtaining accurate ionospheric information, the proposed method can accurately locate the target; ionospheric measurement error greatly affects the location precision; increase the number of sites can improve location precision and reduce the precision requirements of the ionospheric parameters. The simulation results provide a theoretical basis for the development of the short wave TDOA location system and the precision requirement of the ionospheric parameters.

TDOA location; raytracing; ionosphere model; location error

攸陽, 錢志剛, 李吉寧, 等. 短波時差定位中電離層參數對定位影響仿真[J]. 電波科學學報,2017,32(4):462-466.

10.13443/j.cjors.2017033002

YOU Y, QIAN Z G, LI J N, et al. Simulation on the effect of ionospheric parameters on TDOA location in short wave[J]. Chinese journal of radio science,2017,32(4):462-466. (in Chinese). DOI: 10.13443/j.cjors.2017033002

TN01

A

1005-0388(2017)04-0462-05

DOI10.13443/j.cjors.2017033002

2017-03-30

國家自然科學基金(No.61331012)

聯系人： 李吉寧 E-mail: ljnsf@126.com