基于尺度變換的寬帶線性調頻信號時差/尺度差估計算法

郭付陽 張子敬 楊林森

(西安電子科技大學 雷達信號處理國家重點實驗室,西安 710071)

基于尺度變換的寬帶線性調頻信號時差/尺度差估計算法

郭付陽 張子敬 楊林森

(西安電子科技大學 雷達信號處理國家重點實驗室,西安 710071)

提出了一種基于尺度變換的寬帶線性調頻信號時差和尺度差的快速算法. 根據兩路接收到的線性調頻信號間調頻率之比為尺度差的平方的特點,利用分數階傅里葉變換分別估計出兩路信號的調頻率,即可獲得尺度差的估計. 將估計的尺度差對一路信號進行伸縮,并計算伸縮后信號與另一接收信號的時域相關,根據相關峰的位置估計出時差. 相比于傳統基于寬帶互模糊函數的方法,該方法避免了二維搜索寬帶互模糊函數的峰值,只需若干次快速傅里葉變換即可實現,能夠顯著降低運算量. 仿真結果顯示該方法在高信噪比下逐漸接近克拉美-羅下界.

分數階傅里葉變換;寬帶互模糊函數;時/尺度差估計;寬帶線性調頻信號; 克拉美-羅下界

引 言

在無源定位中,一種常用的定位方法是利用多個位于不同位置的接收機來接收輻射源信號,通過估計各接收信號間的時差來實現定位. 當接收機和輻射源存在相對運動時,接收機所接收到的信號波形相比于發射信號表現出被拉伸或者壓縮的特性. 對于窄帶信號,該影響可近似認為接收信號相比發射信號的載頻產生了多普勒頻移. 因此,對于窄帶信號,在相對運動存在時,常通過估計兩路信號的時差和多普勒頻差來定位未知的輻射源[1-4]. 然而,對于寬帶信號,繼續沿用多普勒頻移的設定會導致定位出現較大誤差. 為了對輻射源進行精確定位,需要估計的參數為接收信號間的時差和尺度差.

寬帶互模糊函數(Wideband Cross Ambiguity Function, WBCAF)是估計兩路信號間時差和尺度差的常用工具之一[5-7]. WBCAF將兩路信號在時域和尺度域進行二維相關,其峰值的位置對應真實的時差和尺度差. 由于WBCAF與連續小波變換具有相同的表達式,因此WBCAF的計算可通過小波變換來實現. 然而,在無源定位中,接收信號為未知輻射源輻射的信號,其解析式往往未知,直接應用小波變換需要對接收信號進行變采樣率處理,運算量過大,尤其當尺度差接近1時,往往難以實現[8]. 文獻[9]利用互小波變換的性質,分別計算出兩路接收信號相對于某一給定的小波的小波變換,再由小波變換的結果獲得兩路接收信號的WBCAF. 在該方法中,伸縮變換的對象為解析式已知的小波,無需對接收信號進行變采樣率處理,因而降低了部分運算量. 然而,該方法需要聯合兩路接收信號小波變換的結果來計算WBCAF,運算量仍然較大. 文獻[10]提出了一種對離散信號進行尺度變換的快速計算方法,并將之用于WBCAF的計算,能夠有效降低運算量. 不過,該方法仍需二維搜索WBCAF峰值,在尺度差需要搜索的范圍較大時,運算量偏大,不利于實時處理.

本文提出了一種基于尺度變換的時差/尺度差的快速估計方法. 由于線性調頻(Linear Frequency Modulation, LFM)信號在雷達、聲吶等領域的廣泛應用[11-13],本文所針對的信號為寬帶LFM信號. 對于寬帶LFM信號,接收機所接收到的同一輻射源信號間的尺度差的平方等于兩路接收信號調頻率之比. 通過分數階傅里葉變換(Fractional Fourier Transform, FrFT)分別估計出兩路接收信號的調頻率,即可獲得尺度差的估計. 在搜索最優角度的過程中,為了提高搜索效率,采用了分級搜索的結構．利用估計到的尺度差對第一路接收信號進行伸縮,并將伸縮后的信號與另一路接收信號做時域相關,由時域相關峰的位置估計出時差. 與傳統基于WBCAF的方法相比,該方法只需一維搜索出接收的LFM信號所對應的最優角度即可估計得到尺度差,再一維搜索一次時域相關峰的峰值獲得時差的估計. 由于避免了二維搜索模糊函數峰值,并且只需對接收信號做一次尺度變換,該方法能夠顯著降低估計所需的運算量. 仿真實驗表明隨著信噪比的提高,該方法所估計的時差和尺度差的均方誤差逐漸接近克拉美-羅下界.

1 信號模型

兩路接收信號可以表示為[14]

(1)

式中:

(2)

常用估計時差/尺度差的方法是二維搜索WBCAF的峰值. 兩路接收信號r1(t)和r2(t)的WBCAF可以表示為

(3)

式中,(*)表示復共軛. 不考慮噪聲時,式(3)表示為

(4)

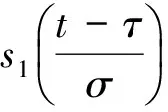
針對上述問題,文獻[10]給出了一種對離散信號進行快速尺度變換的算法,并將該方法用于估計寬帶信號的時差和尺度差. 尺度變換的思路是對接收到的離散信號用Sinc函數重構其對應的連續信號,并對重構后的信號進行伸縮,最后再對伸縮后的信號進行采樣. 尺度變換的快速實現如下所示,假定接收到的離散信號為

x(k)=s(k)+n(k),-N′≤k≤N′,

(5)

則希望得到的尺度變換后的信號為[10]

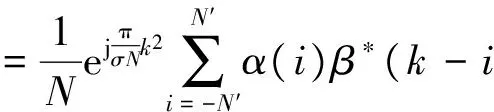
(6)

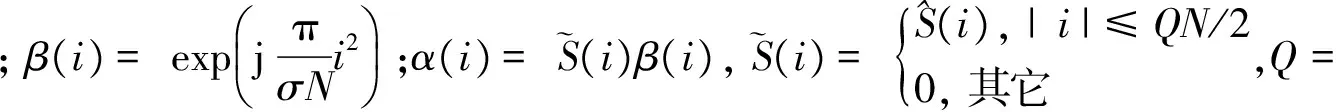
式(4)中的WBCAF可寫為

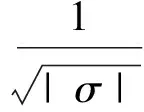
(7)

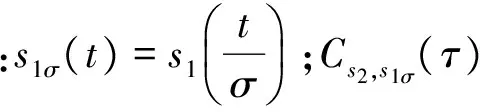
雖然文獻[10]提出的尺度變換方法能夠用于估計時差和尺度差,然而該方法需要對接收信號r1(t)在不同尺度下進行變換,當需要變換的尺度數量變大時,其運算量急劇增大,不利于實時處理. 針對該問題,本文提出了基于尺度變換的時差和尺度差估計方法. 該方法首先利用FrFT估計出兩路接收信號的尺度差,然后用該尺度差對第一路接收信號做伸縮,并將伸縮后的信號與第二路接收信號做時域相關,由相關峰的位置估計出兩路接收信號的時差. 該方法避免了二維搜索模糊函數的峰值,只需對信號進行一次尺度變換,并且可利用快速傅里葉變換(Fast fourier Transform,FFT)實現,能夠顯著降低估計所需的運算量.

2 基于尺度變換的時差/尺度差估計

2.1尺度差的估計

根據式(2),對s1(t)做尺度為1/σ0的伸縮變換并將其延時τ0即可得到

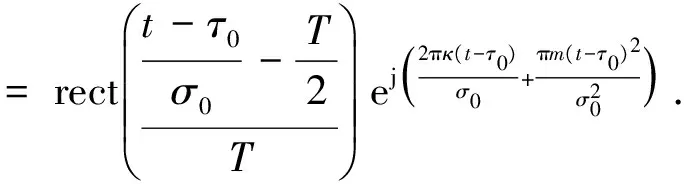
(8)

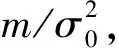
LFM信號調頻率的估計常用FrFT來實現. 某個信號x(t)的FrFT為

(9)

式中,

(10)

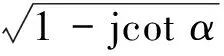
cotαopt=-m．

(11)

因此,估計某個LFM信號x(t)的最優角度可通過搜索x(t)在不同角度上的FrFT的峰值來實現,FrFT取到最大值所對應的角度即為最優的角度,有

(12)

當LFM信號x(t)湮沒在白噪聲中時,式(12)仍然可以直接用于估計最優角度,這是因為白噪聲在任意角度的FrFT不會形成峰值. 假設s1(t)所對應的最優角度為α1,s2(t)所對應的最優角度為α2,則兩路信號最優角度的估計為

(13)

式中,R1,α(u)和R2,α(u)分別為接收信號r1(t)和r2(t)在角度α的FrFT. 結合式(11)和式(13),獲得尺度差的估計為

(14)

在搜索LFM信號對應的最優角度時,為了降低運算量,可以采用分級搜索來減少搜索角度的個數,一般只需三級分級搜索即可搜索到最優角度．FrFT需要搜索的初始角度范圍為[-π/2,π/2],假設初始搜索步長為Δα,且有0<Δα<π,采用三級分級搜索的步驟為:

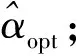
分級搜索的優勢在于可以用較低的運算量獲得同樣的角度精度．在采用三級分級搜索時,可以看到,當搜索角度的精度為Δα/100時,步驟1需要搜索的角度數為π/Δα,步驟2和步驟3分別需要搜索20個角度,因此采用三級搜索只需搜索π/Δα+40個角度,而如果直接以Δα/100搜索整個角度范圍需要搜索100π/Δα個角度.由于0<Δα<π,顯然在搜索最優角度時采用分級搜索能夠顯著減少運算量.

2.2時差的估計

(15)

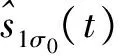
(16)

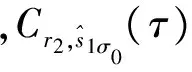
(17)

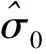
3 運算量分析

本節首先分析了本文所提方法的運算量,接著與文獻[10]中尺度變換方法的運算量進行了對比. 假設處理的信號長度為N,需要搜索的尺度個數為L.

估計尺度差主要的運算量為計算FrFT,根據文獻[18]中FrFT的快速算法,一次FrFT所需的復乘次數為3Nlog2N+3N, 由于需要對兩路信號都做FrFT,因此一個角度下的FrFT需要進行6Nlog2N+6N次復乘. 雖然需要搜索的角度個數為L,然而通過分級搜索可將搜索的角度減少為M(M一般為幾十),因此估計尺度差需要的復乘次數約為6MNlog2N+6MN. 時差估計的運算量分為兩部分:文獻[10]中給出了信號進行一次尺度變換所需的復乘次數為4Nlog2N+4N;時域相關利用FFT來實現,包括三次FFT和一次信號點乘,一次時域相關需要計算3Nlog2N+N次復乘. 因此,運用本文方法所需的復乘次數約為6MNlog2N+6MN+7Nlog2N+5N.

文獻[10]中的尺度變換方法在一個尺度下所需的運算量與本文方法估計時差時候的運算量一致,需要的復乘次數為7Nlog2N+5N,因此L個尺度下需要計算7LNlog2N+5LN次復乘.

表1為不同信號點數N下的本文方法與尺度變換方法的運算量對比,假設需要搜索的尺度個數L=1 000,則采用三級分級搜索后需要搜索的尺度個數M=50. 從表1可以看到,運用本文方法估計時差和尺度差所需的運算量要遠少于尺度變換方法.

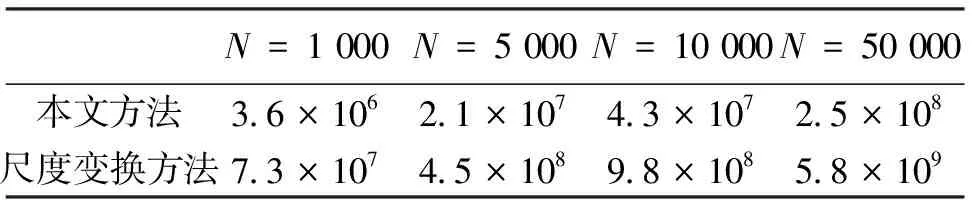
表1 本文方法與尺度變換方法運算量對比

4 仿真實驗

本節首先給出了本文方法在低信噪比下所估計到的時差和尺度差的仿真;接著,在不同信噪比下,對比了本文方法和尺度變換方法的估計性能,并與克拉美-羅下界進行了比較.

4.1尺度差和時差的估計

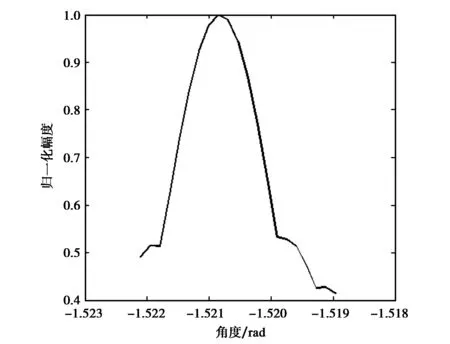
圖1 第一路接收信號的分數階傅里葉變換

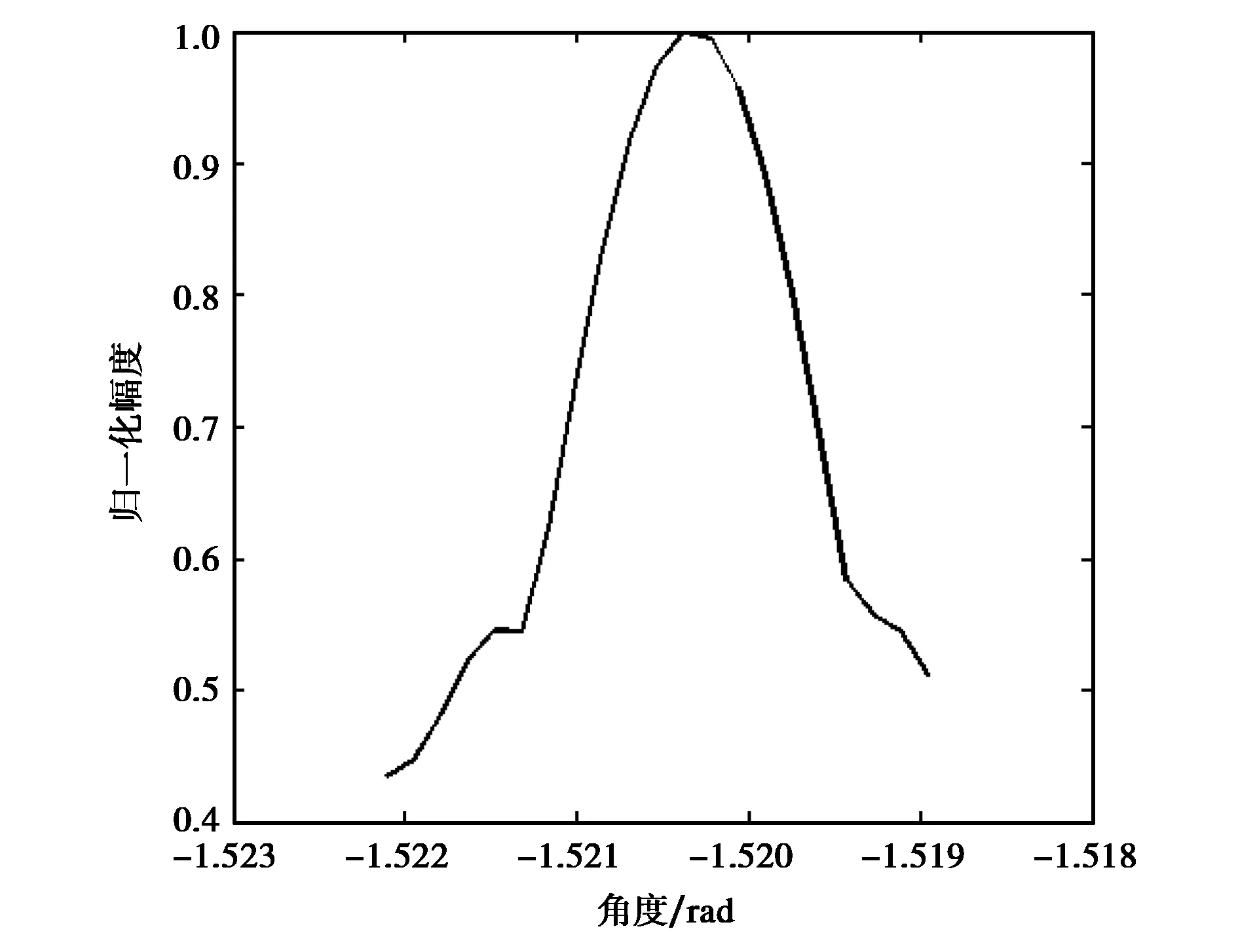
圖2 第二路接收信號的分數階傅里葉變換

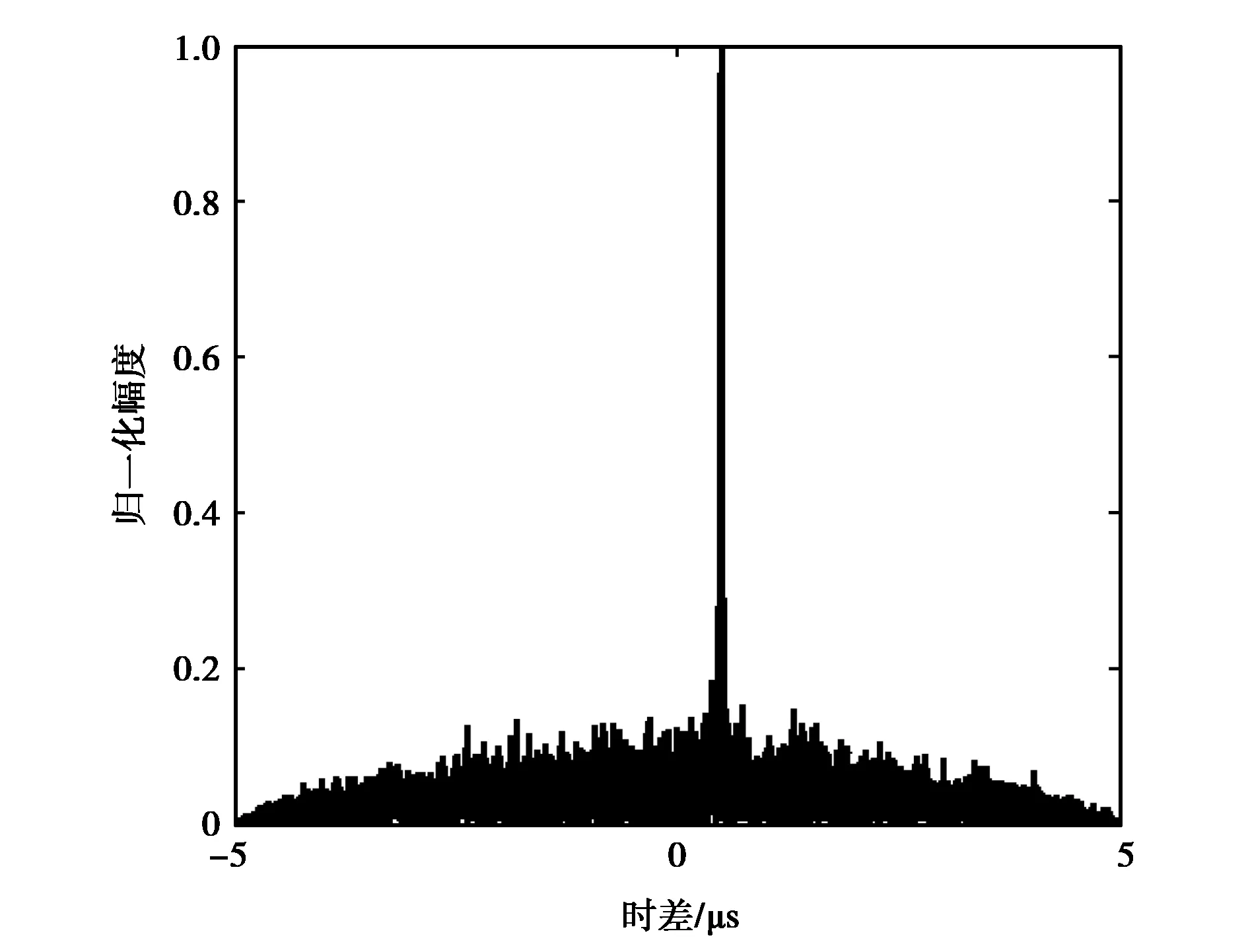
圖3 時域相關結果

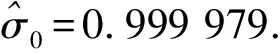
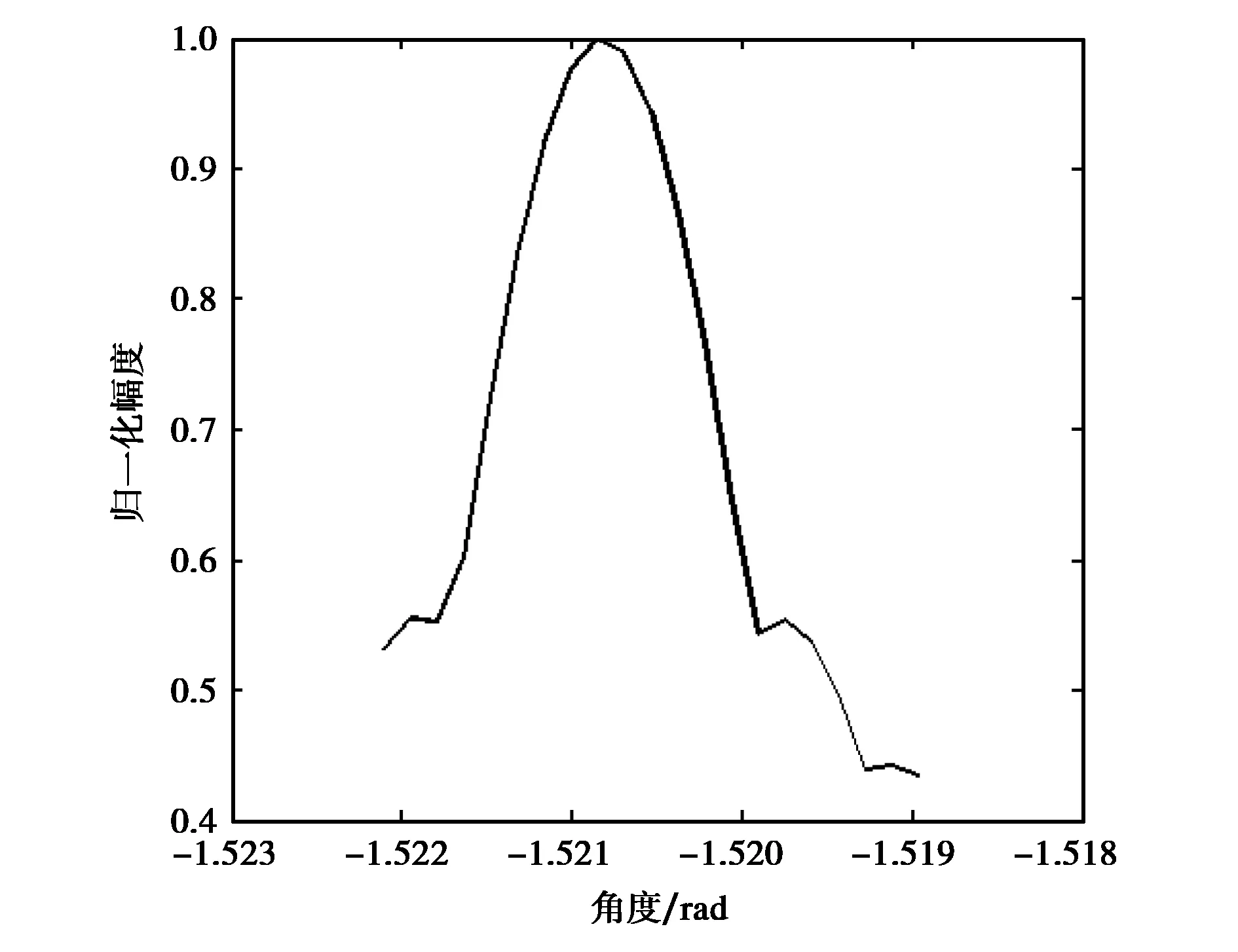
圖4 第一路接收信號的分數階傅里葉變換

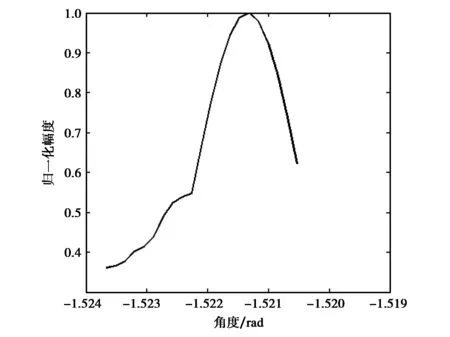
圖5 第二路接收信號的分數階傅里葉變換

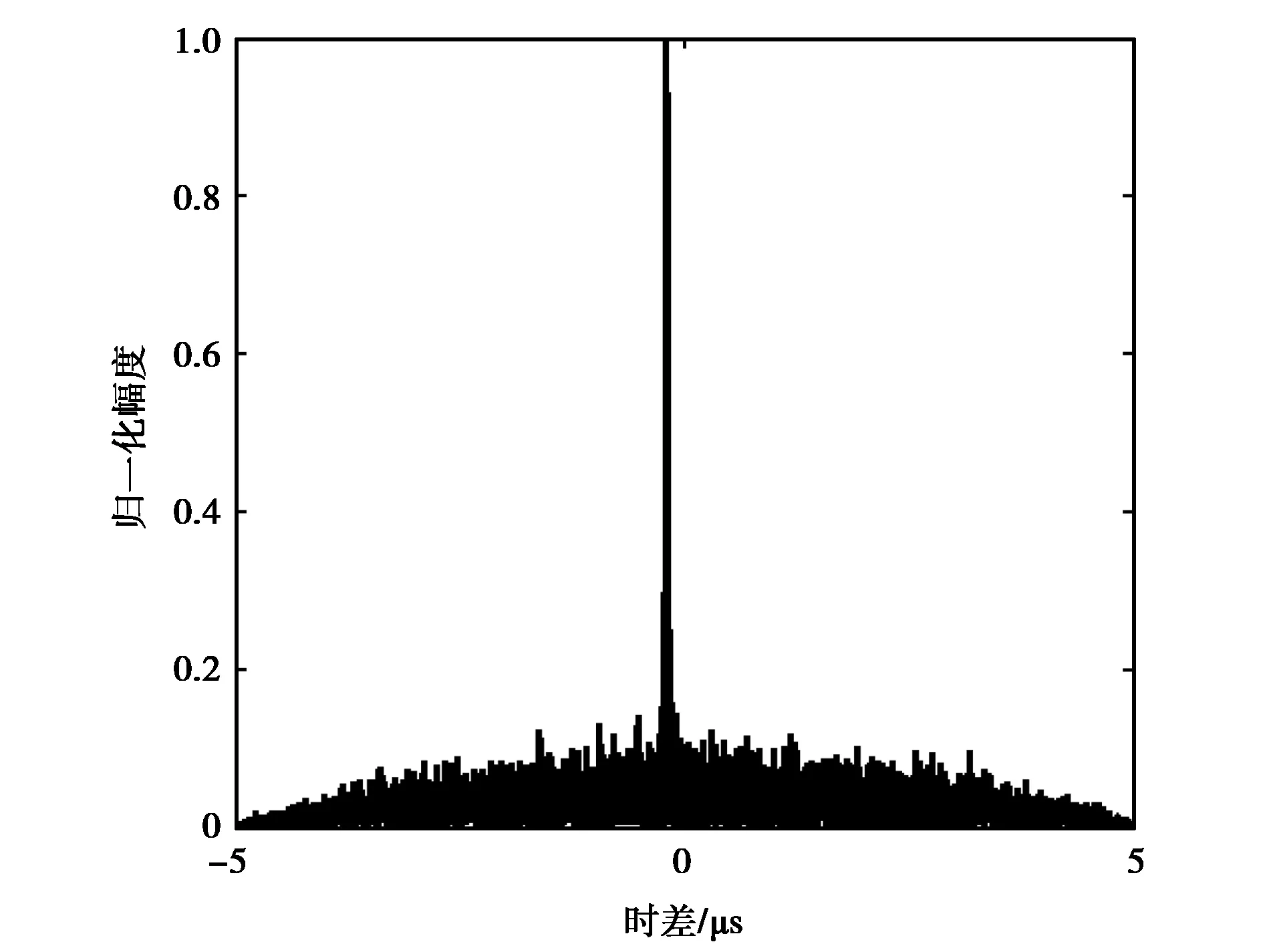
圖6 時域相關結果

4.2均方根誤差以及估計時間的對比

在不同信噪比下,仿真了利用本文方法和尺度變換方法所估計到的時差和尺度差的均方根誤差,并與克拉美-羅下界進行了對比. 克拉美-羅下界的仿真曲線根據文獻[9]中給出的寬帶信號時差/尺度差估計的克拉美-羅下界公式所獲得. 圖7為時差估計的均方根誤差仿真圖,圖8為尺度差估計的均方根誤差仿真圖. 從圖7和圖8可以看到:本文方法與尺度變換方法所估計的均方根誤差曲線基本一致;隨著信噪比的提高,兩種方法所估計到的時差和尺度差的均方根誤差均明顯降低,并逐漸接近克拉美-羅下界.

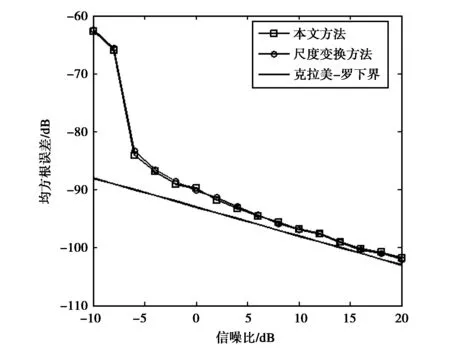
圖7 時差估計的均方誤差曲線

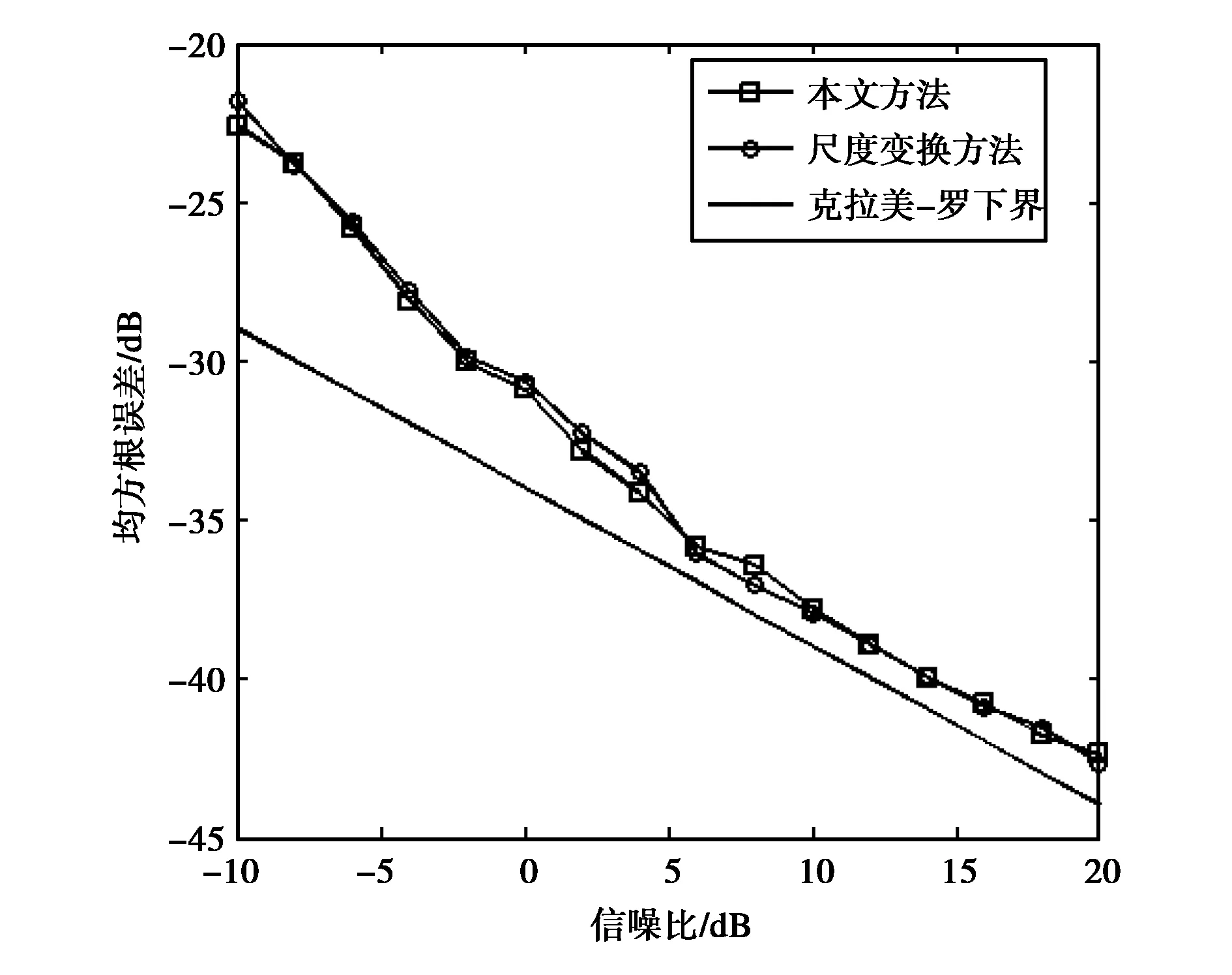
圖8 尺度差估計的均方誤差曲線

圖9為本文方法與尺度變換方法估計時差和尺度差所需CPU時間的對比圖.仿真中采樣率fs=500 MHz,所需搜索的尺度個數L=1 000,運用本文方法估計時,通過采用三級分級搜索處理結構,所需搜索的角度個數減少為M=50. 由圖9可看出:本文方法所需的估計時間要明顯少于尺度變換的方法;尤其在處理長信號時,運用本文方法能夠更好滿足實時處理的要求.

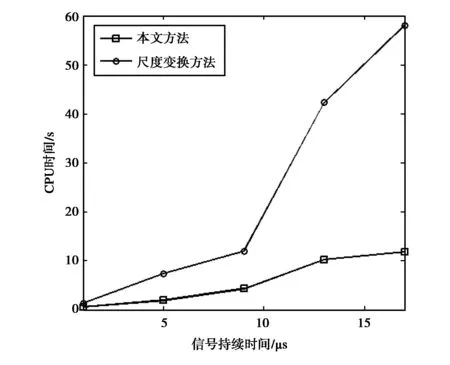
圖9 本文方法與尺度變換方法估計時間對比

5 結 論

針對傳統的時差/尺度差估計方法存在運算量大導致無法實時估計的問題,本文提出了一種寬帶線性調頻信號的時差和尺度差估計的快速算法．該方法通過估計信號的調頻率來獲得尺度差的估計,進而計算WBCAF在尺度差處的切片來獲得時差的估計．與傳統的尺度變換方法相比,該方法僅需對信號進行一次伸縮,能夠有效提高估計效率．仿真實驗證明,本文提出的方法能夠在不損失估計性能的同時顯著提高估計的效率,能夠實時估計出時差和尺度差．

[1] 孫正波, 葉尚福. 一種時差/頻率差快速聯合估計方法[J]. 電波科學學報, 2006, 21(5): 641-646.

SUN Z B, YE S F. Fast algorithm for joint estimation of DTO and DFO[J]. Chinese journal of radio science, 2006, 21(5): 641-646. (in Chinese)

[2] KIM Y H, KIM D G, KIM H N. Two-step estimator for moving-emitter geolocation using time difference of arrival/frequency-difference of arrival measurements[J]. IET radar, sonar & navigation, 2015, 9(7): 881-887.

[3] HO K C, LU X, KOVAVISARUCH L. Source localization using TDOA and FDOA measurements in the presence of receiver location errors: Analysis and solution[J]. IEEE transactions on signal processing, 2007, 55(2): 684-696.

[4] AMAR A, LEUS G, FRIEDLANDER B. Emitter localization given time delay and frequency shift measurements[J]. IEEE transactions on aerospace and electronic systems, 2012, 48(2): 1826-1837.

[5] STEIN S. Algorithms for ambiguity function processing[J]. IEEE transactions on aerospace and signal processing, 1981, 29(3): 588-599.

[6] SHARIF M R, ABEYSEKERA S S. Efficient wideband signal parameter estimation using a radon-ambiguity transform slice[J]. IEEE transactions on AES, 2007, 43(2): 673-688.

[7] 孫正波, 葉尚福. 利用互模糊函數實現衛星干擾源定位[J]. 電波科學學報, 2004, 19(5): 525-529.

SUN Z B, YE S F. Satellite interference location using cross ambiguity function[J]. Chinese journal of radio science, 2004, 19(5): 525-529. (in Chinese)

[8] WEISS L G. Wavelets and wideband correlation processing[J]. IEEE signal processing magazine, 1994, 11(1): 13-32.

[9] NIU X X, CHING P C. Wavelet based approach for joint time delay and Doppler stretch measurements[J]. IEEE transactions on aerospace and electronic systems, 1999, 35(3): 1111-1119.

[10] HO K C, CHAN Y T. Optimum discrete wavelet scaling and its application to delay and Doppler estimation[J]. IEEE transactions on signal processing, 1998, 46(9): 2285-2290.

[11] CHEN X L, GUAN J, LIU N B, et al. Maneuvering target detection via radon-fractional Fourier transform-based long-time coherent integration[J]. IEEE transactions on signal processing, 2014, 62(4): 939-953.

[12] 朱文濤, 蘇濤, 楊濤, 等. 線性調頻連續波信號檢測與參數估計算法[J]. 電子與信息學報, 2014, 36(3): 552-558.

ZHU W T, SU T, YANG T, et al. Detection and parameter estimation of linear frequency modulation continuous wave signal[J]. Journal of electronics & information technology, 2014, 36(3): 552-558. (in Chinese)

[13] 朱文濤, 蘇濤, 楊濤, 等. 低信噪比下線性調頻連續波信號的參數估計[J]. 電波科學學報, 2013, 28(6): 1158-1164.

ZHU W T, SU T, YANG T, et al. Parameter estimation of linear frequency modulated continuous wave signal in low SNR[J]. Chinese journal of radio science, 2013, 28(6): 1158-1164. (in Chinese)

[14] FOWLER M L, HU X. Signal models for TDOA/FDOA estimation[J]. IEEE transactions on aerospace and electronic systems, 2008, 44 (4): 1543-1549.

[15] 杜雨洺, 楊建宇. 基于FRFT的LFMCW雷達加速動目標檢測與參數估計[J]. 電波科學學報, 2005, 20(6): 815-819.

DU Y M, YANG J Y. Novel method of moving target detection and parameter estimation for LFMCW radar[J]. Chinese journal of radio science, 2005, 20(6): 815-819. (in Chinese)

[16] 李會勇, 許丁文, 胡進峰, 等. 基于FRFT的天波雷達多機動目標檢測[J]. 系統工程與電子技術, 2014, 36(9): 1725-1730.

LI H Y, XU D W, HU J F, et al. FRFT based algorithm for maneuvering target detection with OTH radar[J]. Systems engineering and electronics, 2014, 36(9): 1725-1730. (in Chinese)

[17] OONINCX P J. Joint time-frequency offset detection using the fractional Fourier transform[J]. Signal processing, 2008, 88: 2936-2942.

[18] OZAKTAS H M, ARIKAN O, KUTAY M A, et al. Digtal computation of the fractional Fourier transform[J]. IEEE transactions on signal processing, 1996, 44(9): 2141-2150.

郭付陽(1991—),男,江西人,博士研究生,研究方向為無源定位、雷達信號處理.

張子敬(1967—),男,陜西人,教授,博士生導師,研究方向為無源定位、雷達信號處理.

楊林森(1988—),男,陜西人,博士研究生,研究方向為無源定位、雷達信號處理.

Scaling-basedTDOA/SDOAestimationalgorithmforwidebandchirpsignals

GUOFuyangZHANGZijingYANGLinsen

(NationalLabofRadarSignalProcessing,XidianUniversity,Xi’anShaanxi710071,China)

A method based on scaling is proposed to estimate the time difference of arrival (TDOA) and scale difference of arrival (SDOA) between two

wideband chirp signals. Using the relation that the square of SDOA equals to the ratio of chirp-rates of two received chirp signals, each chirp-rate of two chirp signals is first estimated using the fractional Fourier transform, and then the SDOA can be evaluated. By scaling one received chirp signal with the estimated SDOA and evaluating the correlation of the scaled chirp signal and the other received chirp signal, the TDOA is finally estimated. Since the 2-D searching of the peak position of the wideband cross ambiguity function is avoided and it can be evaluated using only few fast Fourier transforms, the computational cost is significantly reduced. Simulation results show that the root mean square errors of the estimated TDOA and SDOA using proposed method closely meet to the Cramer-Rao lower bound under high signal-to-noise ratios.

fractional Fourier transform(FrFT); wideband cross ambiguity ambiguty(WBCAF); TDOA/SDOA estimation; wideband chirp signal;Cramer-Rao lower bound

郭付陽, 張子敬, 楊林森. 基于尺度變換的寬帶線性調頻信號時差/尺度差估計算法[J]. 電波科學學報,2017,32(4):441-448.

10.13443/j.cjors.2017060201

GUO F Y, ZHANG Z J, YANG L S. Scaling-based TDOA/SDOA estimation algorithm for wideband chirp signals[J]. Chinese journal of radio science,2017,32(4):441-448. (in Chinese). DOI: 10.13443/j.cjors.2017060201

TN911.7

A

1005-0388(2017)04-0441-08

DOI10.13443/j.cjors.2017060201

2017-06-02

國家自然科學基金(No.61571349)

聯系人： 張子敬 E-mail: zjzhang@xidian.edu.cn