一種基于可靠度約束的分階段等周期預(yù)防性維修模型研究
席啟超, 曹繼平, 陳桂明, 常雷雷, 熊奇, 王賽
(1.96717部隊, 浙江 金華 321006; 2.火箭軍工程大學(xué) 裝備管理工程系, 陜西 西安 710025)
一種基于可靠度約束的分階段等周期預(yù)防性維修模型研究
席啟超1,2, 曹繼平2, 陳桂明2, 常雷雷2, 熊奇2, 王賽2
(1.96717部隊, 浙江 金華 321006; 2.火箭軍工程大學(xué) 裝備管理工程系, 陜西 西安 710025)
為保持裝備壽命周期的運行可靠性,針對周期預(yù)防性維修模型和順序預(yù)防性維修模型的優(yōu)缺點,結(jié)合裝備維護保養(yǎng)實際,提出3階段等周期預(yù)防性維修模型。以可靠度約束條件下的裝備壽命周期最小費率為優(yōu)化目標,建立了周期預(yù)防性維修模型、順序預(yù)防性維修模型和3階段等周期預(yù)防性維修模型,從而得到各計算模型裝備壽命周期的最優(yōu)預(yù)防性維修次數(shù)和維修間隔期。結(jié)果表明,在同等條件下,3階段等周期預(yù)防性維修模型既能保持裝備壽命周期內(nèi)較高的可靠性和較低的費率,又能緊密結(jié)合維修操作實際,具有良好的應(yīng)用可行性和推廣性。
兵器科學(xué)與技術(shù); 可靠度; 預(yù)防性維修; 最小費率; 維修次數(shù); 維修間隔期
0 引言
根據(jù)預(yù)防性維修活動的時間間隔,一般將預(yù)防性維修分為周期預(yù)防性維修和順序預(yù)防性維修。從維修效果來看,周期預(yù)防性維修將系統(tǒng)的劣化過程近似為均勻的劣化過程,采取等時間間隔的預(yù)防性維修活動。黃傲林等[1]針對軍事裝備的日常維護保養(yǎng)實際,以裝備壽命周期的最小費率C(N,T)為決策因素,采用比例壽命回退模型,對裝備壽命周期內(nèi)的預(yù)防性維修次數(shù)N和維修周期T進行了求解。Zhou等[2]在此基礎(chǔ)上增加了可靠度約束,并以費率為決策因素對N和T進行了求解。由于等間隔期維修良好的實踐應(yīng)用性,目前仍有許多學(xué)者研究周期預(yù)防性維修[3-5],該策略的優(yōu)點是方便日常的裝備管理,缺點是由于多數(shù)裝備的劣化過程并非均勻。采取該措施,一方面隨著裝備使用時間增加,中后期故障率增速加大,周期預(yù)防性維修活動有效性不強;另一方面,維修時機與故障規(guī)律貼合不夠緊密,產(chǎn)生一定程度的“過維修”或“欠維修”,導(dǎo)致一定的維修資源浪費。順序預(yù)防性維修則更加緊密結(jié)合裝備的故障率,采取時間間隔不等的預(yù)防性維修方式,文獻[6-11]都對順序預(yù)防性維修進行了深入研究,其優(yōu)點是理論上的維修時機更加準確,維修資源的利用率更高,采取該措施可使裝備的故障率保持在更低的水平;缺點是實踐中不等間隔維修不便于裝備維修和管理。因此,目前在裝備的實際維修過程中多數(shù)仍是采取周期預(yù)防性維修方式。
某型發(fā)射裝備科技集成度高,可靠性比普通機械類產(chǎn)品高,完成作戰(zhàn)任務(wù)的要求高。針對這類裝備,本文結(jié)合以上兩種維修方式的特點,以裝備的可靠度為約束,以壽命周期費率為決策目標,通過采用役齡回退模型,建立了一種分階段等周期預(yù)防性維修模型,并將此模型與傳統(tǒng)的周期預(yù)防性維修和順序預(yù)防性維修模型進行了對比分析。通過算例分析比較表明,分階段等周期預(yù)防性維修策略更具有一般性,而3階段等周期預(yù)防性維修既能保證可靠性前提下的經(jīng)濟性,又具備良好的應(yīng)用可行性。
1 基本假設(shè)與問題描述
1.1 基本假設(shè)
1)模型中的預(yù)防性維修為狹義的預(yù)防性維修,不包含更換維修,不能使裝備恢復(fù)如新,預(yù)防性更換可使裝備恢復(fù)如新,預(yù)防性維修和預(yù)防性更換都可提高裝備可靠度。
2)裝備每運行Ti時間進行第i次預(yù)防性維修,在第i次與第i+1次預(yù)防性維修之間發(fā)生故障采取最小維修,最小維修只使裝備恢復(fù)正常運行狀態(tài),裝備可靠度與維修前保持不變。
3)由于最小維修的時間相對于裝備運行時間很小,故在壽命周期內(nèi)最小維修時間忽略不計。
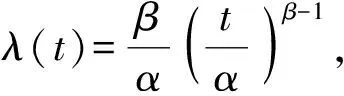
1.2 問題描述
裝備壽命周期內(nèi)的單位時間維修成本用維修費率C(N,T)表示,壽命周期內(nèi)的維修總成本Ctot包括預(yù)防性維修總費用Cp,最小維修總費用Cm,預(yù)防性更換費用cr以及停機損失總費用Cs,裝備只在壽命周期結(jié)束時采取一次預(yù)防性更換,壽命周期內(nèi)每次發(fā)生故障時采取最小維修方式。裝備壽命周期總時間Ttot包括預(yù)防性維修間隔期Ti的總和,預(yù)防性維修時間tp,i的總和以及預(yù)防性更換時間tr.
cp,i為第i次預(yù)防性維修費用,隨著維修次數(shù)的增加而增加,可表示為cp,i=cf+icv,其中cf為基本維修費用,cv為動態(tài)維修費用,一般cf和cv可由維修經(jīng)驗獲得。
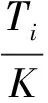
為了描述第i次預(yù)防性維修間隔期內(nèi)平均故障次數(shù),本文借鑒文獻[12]中的役齡回退模型,如圖1所示。每次預(yù)防性維修都使裝備的實際使用壽命回退一定量,回退量占預(yù)防性維修間隔期的比值即為役齡回退因子,其物理意義表示每一次的預(yù)防性維修對裝備的恢復(fù)程度。役齡回退因子與預(yù)防性維修次數(shù)和投入的預(yù)防性維修費用有關(guān),且一般隨著故障率的遞增呈下降趨勢。由于預(yù)防性維修投入越多,役齡回退量越大。工程實踐表明,對于普通的磨損類機械故障,同等維修投入條件下,隨著維修次數(shù)的增加,役齡回退量遞減速度大于線性遞減速度,并且一般條件下,役齡回退量隨著維修投入成本的增加,役齡回退量減少的趨勢逐漸放緩,因此本文將役齡回退因子表示為Δi=abi,i=1,2,…,N-1,其中a為維修費用調(diào)整因子,b為維修次數(shù)修正系數(shù)。

圖1 役齡回退與預(yù)防性維修間的時序關(guān)系圖Fig.1 Temporal relationship between service age reduction and preventive maintenance

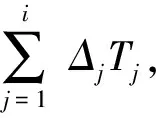

(1)
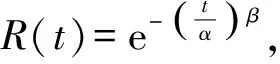
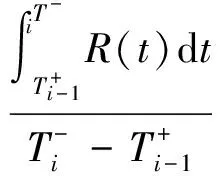
(2)
2 模型建立
2.1 模型1:周期預(yù)防性維修模型
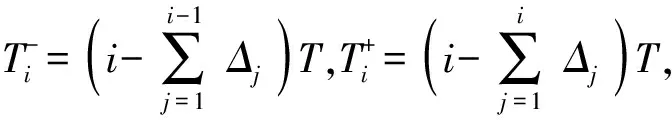
優(yōu)化模型為

(3)
式中:N、T為決策變量,并滿足以下可靠度的約束關(guān)系為

(4)
cm為平均每次最小維修費用;cs為單位時間停機損失費用;T為預(yù)防性維修周期;N為預(yù)防性維修次數(shù);tm為平均每次最小維修所需時間;其他符號含義同上文。
模型的求解方法有兩種:一種是采取邊際分析法使得壽命周期費率C1(N,T)同時滿足C1(N*,T)≤C1(N*+1,T)和C1(N*,T)≤C1(N*-1,T)(N*為最佳預(yù)防性維修次數(shù)),確定N*后就可以求得最小費率時的維修周期T[1,14];另外一種是通過編程進行可行域搜索,求出滿足約束條件可行域內(nèi)所有N、T和C1(N,T),從而求出最優(yōu)解,本文采取的是可行域搜索法。
2.2 模型2:順序預(yù)防性維修模型
優(yōu)化模型為

(5)
式中:N、Ti(i=1,2,…,N)為決策變量,并滿足以下可靠度的約束關(guān)系為

(6)
模型的求解采用可行域搜索法[7],求出滿足約束條件可行域內(nèi)的所有N、Ti和C2(N,T),從而求出最優(yōu)解;或者采取仿真方法進行求解[15],本文采取可行域搜索法。
2.3 模型3:分階段等周期預(yù)防性維修模型
無論是裝備維修計劃制定還是裝備使用維修過程,裝備管理和使用者都傾向于將裝備劃分為3個等級:一是較新裝備;二是一般裝備;三是老舊裝備。這樣的劃分既是裝備役齡的體現(xiàn),也是宏觀經(jīng)驗對裝備故障率的定性分析,更重要的是如此分類便于裝備的日常管理和維修,比如新裝備要重視初始保養(yǎng),一般裝備要重視日常保養(yǎng),老舊裝備要重視恢復(fù)保養(yǎng)。而任何裝備的壽命周期也是由新到一般再到老舊,其劣化過程符合一般規(guī)律,便于定性分析。對于預(yù)防性維修,通過建立3階段等周期預(yù)防性維修模型進行定量分析,N1、N2、N3分別為第1個階段、第2個階段、第3個階段的預(yù)防性維修次數(shù),其中,N3包含最后一次預(yù)防性更換維修。
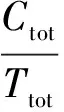
(7)
式中:N1、N2、N3、Ti(i=N1,N2,N3)為決策變量,并滿足以下的約束關(guān)系為
(8)
3 模型仿真求解
以上3個模型采取的可行域搜索算法是在Matlab軟件環(huán)境下通過編程實現(xiàn)。
模型1、模型2算法步驟為:1)代入相關(guān)參數(shù)值,令N=1;2)運用Matlab非線性約束優(yōu)化工具求解優(yōu)化模型,記錄維修間隔期為T*(T*為N維向量)時的最小費率C*;3)令N=N+1,用同樣方法再次求解此時的T*和C*并比較C*(N)與C*(N-1);4)如果C*(N) 3.1 模型參數(shù) 通過維修分析以及歷史故障數(shù)據(jù)統(tǒng)計,某型發(fā)射裝備某部件的各參數(shù)值如表1所示。 將以上參數(shù)值分別代入模型1,模型2和模型3,可以得到該裝備的3種維修策略的計算結(jié)果。 表1 模型參數(shù) 3.2 模型1 當預(yù)防性維修次數(shù)N取不同的值時,每次預(yù)防性維修的壽命周期費率C1(N,T)如圖2、圖3所示,當N=12時出現(xiàn)極值點,此時的最小壽命周期費率C1(N,T)=1 077.947元/d,T=53.466 d,裝備在可靠度大于0.85的前提下,壽命周期為641.6 d. 圖2 不同預(yù)防性維修次數(shù)與費率的關(guān)系Fig.2 Relationship between preventive maintenance frequency and cost rate 圖3 不同預(yù)防性維修次數(shù)與費率的關(guān)系(局部放大)Fig.3 Relationship between preventive maintenance frequency and cost rate (partially magnified view) 在采取等周期預(yù)防性維修措施的情況下,壽命周期內(nèi)維修次數(shù)N越多,維修周期T越短,如圖4所示,這也與維修操作實際相吻合。圖5則反映了取得最小壽命周期費率時各維修周期Ti的平均可靠度Ri在裝備壽命周期內(nèi)的變化情況,由此可知該模型的維修策略能使裝備在壽命周期內(nèi)保持較高的可靠度。 圖4 預(yù)防性維修次數(shù)與維修周期的關(guān)系Fig.4 Relationship between preventive maintenance frequency and maintenance interval 圖5 平均可靠度變化趨勢Fig.5 Variation trend of average reliability 3.3 模型2 圖6 不同預(yù)防性維修次數(shù)與費率的關(guān)系Fig.6 Relationship between preventive maintenance frequency and cost rate 圖7 不同預(yù)防性維修次數(shù)與費率的關(guān)系(局部放大)Fig.7 Relationship between preventive maintenance frequency and cost rate (partially magnified view) 圖6與圖7反映了順序預(yù)防性維修模型的維修次數(shù)N與壽命周期費率C2(N,Ti)的關(guān)系。當N=18時取得最小費率C2(N,Ti)=751.724元/d,此時的預(yù)防性維修間隔期如表2所示,裝備在可靠度大于0.85的條件下,壽命周期為1 025.186 d. 由預(yù)防性維修間隔期縮短的趨勢可知,隨著裝備役齡的增加,裝備的預(yù)防性維修更加頻繁,維修過程與裝備劣化過程貼合較為緊密。由圖8可見裝備的各預(yù)防性維修間隔期平均可靠度下降較為明顯。 3.4 模型3 圖9反映了3階段等周期預(yù)防性維修次數(shù)N1+N2+N3與壽命周期費率C3(N,Ti)的關(guān)系,當3階段預(yù)防性維修次數(shù)分別為N1=5次,N2=5次,N3=6次時,壽命周期費率最低為C3(N,T)=825.69元/d,此時的預(yù)防性維修間隔期如表3所示,裝備在可靠度大于0.85的前提下,壽命周期為897.8 d. 平均可靠度Ri變化規(guī)律如圖10所示,平均可靠度在每個階段結(jié)束后增幅較大,從而使壽命周期的整體可靠度保持在了一個較高水平。 表2 最小費率時的預(yù)防性維修間隔期Ti 圖8 平均可靠度變化趨勢Fig.8 Variation trend of average reliability 表3 最小費率時的預(yù)防性維修間隔期Ti 圖10 平均可靠度變化趨勢Fig.10 Variation trend of average reliability 從3種仿真結(jié)果可以看出,在降低裝備壽命周期費率和提高裝備壽命周期平均可靠度上,3種模型的優(yōu)劣顯而易見。 4.1 在裝備壽命周期費率方面 在相同可靠度的約束條件下,模型1的最優(yōu)維修費率最大且壽命周期最小,僅為641.6元/d,充分說明周期預(yù)防性維修的維修時機選擇還不夠恰當,每次等周期維修導(dǎo)致減緩裝備可靠性降低的力度有限,另外,因受制于給定可靠度下限,導(dǎo)致裝備的壽命周期較短,但是由于等周期的預(yù)防性維修方式容易操作,所以目前在裝備的日常維護保養(yǎng)中,這種方式依然是一種主要的預(yù)防性維修方式。模型2的最優(yōu)維修費率最小且壽命周期最長,為1 025.186元/d,優(yōu)點非常明顯。這種策略是隨著裝備役齡的增加、裝備劣化程度的加劇,預(yù)防性維修的間隔期逐次遞減,所以每次的維修時機與故障率結(jié)合比較緊密,然而正是因為每次都能取得理論上的最佳維修時間,導(dǎo)致每次的維修間隔期不一,維修計劃制定難度大、維修工作較為復(fù)雜,導(dǎo)致該策略的應(yīng)用性大大受限。模型3的最優(yōu)維修費率為825.69元/d,比模型2高出9.84%,比模型1低了23.4%,即費率接近達到最優(yōu)費率,可比多數(shù)裝備現(xiàn)行的周期預(yù)防性維修節(jié)約23.4%的費率,該策略較優(yōu)。 4.2 在裝備壽命周期平均可靠度方面 由圖5、圖8和圖10可知,模型1、模型2和模型3的壽命周期平均可靠度分別為0.968、0.921和0.942. 雖然各個模型都能使裝備可靠度保持在給定范圍以內(nèi),但是模型2的平均可靠度最低,可見模型2最優(yōu)費率的取得是以降低部分可靠性為代價的。 模型3較之模型1和模型2,在每個階段切換之初的維修間隔期的平均可靠度都有一個較大幅度提升,這也正是分階段等周期預(yù)防性維修不同于周期預(yù)防性維修和順序預(yù)防性維修的本質(zhì)所在,分階段等周期預(yù)防性維修是對階段的模塊式優(yōu)化,而周期預(yù)防性維修是從裝備的整個壽命周期角度進行整體優(yōu)化,順序預(yù)防性維修則是對每次的預(yù)防性維修間隔期都力求最優(yōu)。因此,每個維修間隔期的平均可靠度,模型1和模型2都呈現(xiàn)遞減趨勢,而模型3則在階段內(nèi)呈遞減趨勢,階段之間出現(xiàn)平均可靠度的躍升現(xiàn)象。 4.3 可靠度約束對模型的影響 劣化型裝備預(yù)防性維修時機的確定,既與裝備可靠度下降的速度有關(guān),也與可靠度的約束下限有關(guān),可靠度下降的速度越快,越先達到下限值,越需要及時采取預(yù)防性維修措施。為分析參數(shù)取不同值時對模型的影響,不失一般性,分別計算當可靠度下限值為0.70、0.75、0.80、0.85、0.90、0.95時裝備壽命周期費率的變化規(guī)律,如圖11所示。由圖11可以發(fā)現(xiàn),當可靠度下限值在0.70~0.95之間變化時,考慮維修的經(jīng)濟性,模型3相對模型1和模型2的優(yōu)點與可靠度下限值為0.85時相當,充分說明可靠度下限值在這一范圍波動時,模型3具有很好的魯棒性。 圖11 不同可靠度下限時的費率Fig.11 Cost rates under different reliability constraints 4.4 3階段等周期預(yù)防性維修的優(yōu)勢 模型1本質(zhì)上是模型3階段數(shù)為1時的特例,模型2本質(zhì)上是模型3每個階段只采取一次預(yù)防性維修時的特例。模型3結(jié)合裝備劣化過程和維護保養(yǎng)操作實際,吸收了模型1和模型2的優(yōu)點,既從宏觀上貼合裝備劣化過程,各階段間的預(yù)防性維修間隔期呈減少趨勢;又從微觀上結(jié)合維護保養(yǎng)操作實際,各個預(yù)防性維修階段內(nèi)保持維修間隔期相等,在經(jīng)濟性與可行性之間找到了一個較好的平衡點。 本文針對傳統(tǒng)的周期預(yù)防性維修模型和順序預(yù)防性維修模型,提出基于可靠度約束的分階段等周期預(yù)防性維修模型,并運用此模型對某型裝備的某部件進行了分析、討論。實例以及結(jié)果分析表明,對于一般的劣化型裝備,分階段等周期預(yù)防性維修既能接近達到順序預(yù)防性維修的最優(yōu)維修費率,又兼顧了可靠性和維修操作可行性。并且,當可靠度約束下限值在0.70~0.95區(qū)間時,分階段等周期預(yù)防性維修模型還具有良好的魯棒性,為實際工程應(yīng)用提供了有效的方法指導(dǎo)。下一步,將針對分階段等周期預(yù)防性維修的資源消耗情況展開研究,力圖減少“過維修”和“欠維修”等造成的資源浪費。 References) [1] 黃傲林,李慶民,黎鐵冰,等. 劣化系統(tǒng)周期預(yù)防性維修策略的優(yōu)化[J]. 系統(tǒng)工程與電子技術(shù),2014,36(6):1103-1107. HUANG Ao-lin, LI Qing-min, LI Tie-bing, et al. Optimization of periodic preventive maintenance policies for deterioration repairable system[J]. Systems Engineering and Electronics, 2014, 36(6): 1103-1107. (in Chinese) [2] Zhou Q, Sun Y. Imperfect preventive maintenance model study based on reliability limitation[C]∥ Proceedings of the 1st International Conference on Nanomaterial, Semiconductor and Composite Materials. Singapore: EDP Sciences, 2016: 1-3. [3] Darghouth M N, Aitkadi D, Chelbi A. Joint reliability based design and periodic preventive maintenance policy for systems sold with warranty[J]. Journal of Quality in Maintenance Engineering, 2016, 22(1):2-17. [4] Wang J, Zhou Z, Peng H. Flexible decision models for a two-dimensional warranty policy with periodic preventive maintenance [J]. Reliability Engineering & System Safety, 2017, 162:14-27. [5] 白冬梅,白永生,韓玉成. 基于二維量度的復(fù)雜設(shè)備預(yù)防性維修決策優(yōu)化[J]. 火力與指揮控制,2017,42(2):88-91. BAI Dong-mei, BAI Yong-sheng, HAN Yu-cheng. Optimization research on two-dimensional preventive maintenance decision of complex devices[J]. Fire Control & Command Control, 2017, 42(2): 88-91. (in Chinese) [6] 盛天文,陳曉慧,易樹平. 壽命型設(shè)備的預(yù)防維修策略研究[J]. 計算機集成制造系統(tǒng),2009,15(3):598-603. SHENG Tian-wen, CHEN Xiao-hui, YI Shu-ping. Preventive maintenance policy for life-type equipment[J]. Computer Integrated Manufacturing Systems, 2009,15(3): 598-603. (in Chinese) [7] Sheu S H, Chang C C, Chen Y L. An extended sequential imperfect preventive maintenance model with improvement factors[J]. Communications in Statistics-Theory and Methods, 2012, 41(7):1269-1283. [8] El-ferik S, Ben-daya M. Integrated production maintenance model under imperfect age-based maintenance policy and non-negligible maintenance times[J]. Aisa-Pacific Journal of Operational Research, 2010, 27(4): 539-558. [9] Khatab A. Hybrid hazard rate model for imperfect preventive maintenance of systems subject to random deterioration[J]. Journal of Intelligent Manufacturing, 2015, 26(3):601-608. [10] 蓋京波,孔耀. 有限使用時間內(nèi)預(yù)防性維修策略優(yōu)化[J]. 兵工學(xué)報,2015, 36(11):2164-2172. GAI Jing-bo, KONG Yao. Optimization strategy of preventive maintenance in finite time horizon[J]. Acta Armamentarii, 2015, 36(11): 2164-2172. (in Chinese) [11] 劉歡,劉志剛,姜靜. 基于可靠度約束的接觸網(wǎng)系統(tǒng)預(yù)防性維修策略優(yōu)化研究[J]. 機械強度,2016,38(1):74-79. LIU Huan, LIU Zhi-gang, JIANG Jing. Optimization research of preventive maintenance strategy on the catenary system based on reliability constraints[J]. Journal of Mechanical Strength, 2016, 38(1): 74-79. (in Chinese) [12] 韓幫軍,范秀敏,馬登哲. 基于可靠度約束的預(yù)防性維修策略的優(yōu)化研究[J]. 機械工程學(xué)報,2003, 39(6):102-105. HAN Bang-jun, FAN Xiu-min, MA Deng-zhe. Research on the optimal preventive maintenance policy based on reliability constraints[J]. Journal of Mechanical Engineering, 2003, 39(6): 102-105. (in Chinese) [13] 王雪琴,楊秀香. 關(guān)于連續(xù)函數(shù)平均值的研究[J]. 渭南師范學(xué)院學(xué)報,2015,30(10):22-25. WANG Xue-qin, YANG Xiu-xiang. Research on the average continuous function[J]. Journal of Weinan Normal University, 2015, 30(10): 22-25. (in Chinese) [14] Toshio N. Periodic and sequential preventive maintenance policies[J]. Journal of Applied Probability, 1986, 23(2):536-542. [15] 周曉軍,奚立峰,李杰. 一種基于可靠性的設(shè)備順序預(yù)防性維護模型[J]. 上海交通大學(xué)學(xué)報,2005,39(12):2044-2047. ZHOU Xiao-jun, XI Li-feng, LEE Jay. A reliability-based sequential preventive maintenance model[J]. Journal of Shanghai Jiao Tong University, 2005, 39(12): 2044-2047. (in Chinese) ResearchonaPhasedPeriodicPreventiveMaintenanceModelBasedonReliabilityConstraint XI Qi-chao1,2, CAO Ji-ping2, CHEN Gui-ming2, CHANG Lei-lei2, XIONG Qi2, WANG Sai2 (1.Unit 96717 of PLA, Jinhua 321006, Zhejiang, China; 2.Department of Equipment Management Engineering, Rocket Force University of Engineering, Xi’an 710025, Shaanxi, China) In order to maintain the operational reliability of equipment during life cycle, the advantages and disadvantages of the periodic preventive maintenance model and the sequential preventive maintenance model are analyzed. A three-stage periodic preventive maintenance model is proposed based on the equipment maintenance practices. Three models, i.e., periodic preventive maintenance model, sequential preventive maintenance model and three-stage periodic preventive maintenance model, are constructed by taking the minimum cost rate of equipment life cycle under the reliability constraints as the optimization objective. The optimal preventive maintenance frequencies and intervals of equipment life cycle of each model are obtained. The case study results show that, under the same conditions, a high reliability and a low cost rate of equipment during life cycle can be obtained by using the three-stage periodic maintenance model. Moreover, it can also closely integrate the maintenance operation practices, as well as has a good feasibility and generalizability. ordnance science and technology; reliability; preventive maintenance; minimum cost rate; maintenance frequency; maintenance interval E92 A 1000-1093(2017)11-2251-08 10.3969/j.issn.1000-1093.2017.11.023 2017-04-17 國家自然科學(xué)基金項目(71601180) 席啟超(1986—), 男, 助理工程師, 碩士研究生。 E-mail: 13857993797@163.com 曹繼平(1974—), 男, 副教授, 博士生導(dǎo)師。 E-mail: xacjp@sina.com


4 結(jié)果分析

5 結(jié)論

