國際棉花現(xiàn)貨價(jià)格波動及短期預(yù)測研究

閆慶華,劉維忠,秦 子

(新疆農(nóng)業(yè)大學(xué) 經(jīng)濟(jì)與貿(mào)易學(xué)院,新疆 烏魯木齊 830052)

國際棉花現(xiàn)貨價(jià)格波動及短期預(yù)測研究

閆慶華,劉維忠,秦 子

(新疆農(nóng)業(yè)大學(xué) 經(jīng)濟(jì)與貿(mào)易學(xué)院,新疆 烏魯木齊 830052)

隨著棉花市場化改革的不斷深入,我國棉花市場與國際棉花市場的聯(lián)系日益緊密,同時(shí)我國棉花現(xiàn)貨價(jià)格受國際棉花現(xiàn)貨價(jià)格的影響不斷加深。以2004/2005—2015/2016年國際棉花現(xiàn)貨價(jià)格(Cotlook FE-A)月度數(shù)據(jù)為依據(jù),理論分析了國際棉花現(xiàn)貨價(jià)格的波動情況。基于ARIMA模型實(shí)證預(yù)測了短期內(nèi)國際棉花現(xiàn)貨價(jià)格的波動趨勢,模型相對誤差在5%以下,預(yù)測值精度較高。模型預(yù)測結(jié)果顯示，短期內(nèi)國際棉花現(xiàn)貨價(jià)格呈緩慢上漲趨勢,2017年5月將上升到12812.02元/t,比2016年12月增加了688.83元/t。基于國際棉花現(xiàn)貨價(jià)格的波動趨勢,提出防范國際棉花價(jià)格波動沖擊和保障中國棉花產(chǎn)業(yè)可持續(xù)發(fā)展的對策建議。

ARIMA模型;國際棉花價(jià)格;市場風(fēng)險(xiǎn);短期趨勢

1 前言

當(dāng)前全球棉花消費(fèi)量呈現(xiàn)下降趨勢,但棉花因其天然纖維的良好特性仍占據(jù)全球纖維消費(fèi)市場的重要地位[1]。改革開放以來,我國經(jīng)濟(jì)發(fā)展迅速[2],特別是加入世界貿(mào)易組織(WTO)后,棉花市場與國際棉花市場的聯(lián)系日益緊密,棉紡織工業(yè)在這一時(shí)期得到了快速發(fā)展,成為全球最大的棉花消費(fèi)國和棉花進(jìn)口國[3]。2010/2011年我國實(shí)施了棉花臨時(shí)收儲政策,導(dǎo)致棉花庫存急劇增加,扭曲了國內(nèi)棉花市場的定價(jià)機(jī)制[4],國內(nèi)棉花現(xiàn)貨價(jià)格快速提升,國內(nèi)外棉花價(jià)格差距進(jìn)一步加大,在短期增加棉農(nóng)收入的同時(shí)嚴(yán)重?fù)p害了棉花企業(yè)的利益,造成棉花企業(yè)“用棉難”現(xiàn)象的發(fā)生,迫使國內(nèi)棉花企業(yè)大量采用“物美價(jià)廉”的進(jìn)口棉花[5]。2014/2015年我國實(shí)施棉花目標(biāo)價(jià)格改革政策,將我國棉花企業(yè)與農(nóng)民推向市場,我國棉花現(xiàn)貨價(jià)格受國際棉花需求下降的影響大幅降低,棉花企業(yè)與植棉農(nóng)戶損失慘重。如何在市場化條件下防范國際棉花現(xiàn)貨價(jià)格波動對我國棉花現(xiàn)貨價(jià)格造成嚴(yán)重沖擊,穩(wěn)定我國棉花市場價(jià)格從而保障我國棉花企業(yè)與植棉農(nóng)戶的利益顯得尤為重要。

2 國際棉花現(xiàn)貨價(jià)格波動分析

全球經(jīng)濟(jì)危機(jī)爆發(fā)以來,國際棉花現(xiàn)貨價(jià)格波動劇烈,成為影響我國棉花現(xiàn)貨價(jià)格的重要因素之一。2004/2005—2006/2007年國際棉花現(xiàn)貨價(jià)格走勢平穩(wěn),平均價(jià)格達(dá)到10320.27元/t;2006/2007—2009/2010年國際棉花價(jià)格波動劇烈,2006/2007年以年均8%的增速快速增長到2007/2008年的10925.46元/t,增幅達(dá)到719.03元/t,但2009/2010年再次降低到9476.95元/t,降幅達(dá)到1448.52元/t;2009/2010年至今國際棉花現(xiàn)貨價(jià)格又快速從2009/2010年度的低谷中連續(xù)上漲到歷史高峰,達(dá)到2011/2012年的21943.79元/t,隨后世界棉花現(xiàn)貨價(jià)格持續(xù)走低,目前已回落到2006/2007年的水平,僅為9583.22元/t。我國棉花市場受國際棉花價(jià)格波動的影響較大,變化趨勢與國際棉花現(xiàn)貨價(jià)格變化基本一致,但棉花現(xiàn)貨價(jià)格一直處于較高水平,平均高出世界棉花現(xiàn)貨價(jià)格4000元/t左右,造成國內(nèi)紡織企業(yè)等用棉企業(yè)的成本不斷增加[6]、國際競爭力始終不強(qiáng)等問題,嚴(yán)重影響了我國棉花產(chǎn)業(yè)的健康與可持續(xù)發(fā)展。由于美國棉花種植區(qū)域變化較小、棉花生產(chǎn)技術(shù)較高、棉花產(chǎn)量較穩(wěn)定,且美國棉花除極少部分用于國內(nèi)自給外大部分出口,因此美棉價(jià)格的波動較小(圖1)。

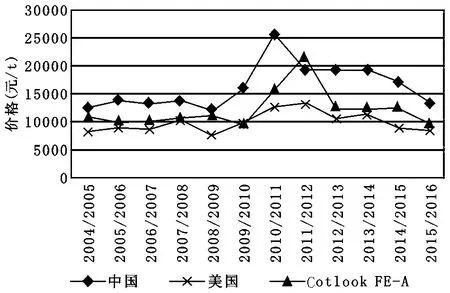
注:根據(jù)美國農(nóng)業(yè)部(USDA)數(shù)據(jù)庫數(shù)據(jù)統(tǒng)計(jì)。

3 基于ARIMA模型的國際棉花現(xiàn)貨價(jià)格短期預(yù)測

國際棉花現(xiàn)貨價(jià)格的形成是一個(gè)復(fù)雜龐大的系統(tǒng),不僅受到全球棉花產(chǎn)量、消費(fèi)量、經(jīng)濟(jì)發(fā)展景氣的影響[7],還受到世界主要產(chǎn)棉國與消費(fèi)國的棉花種植面積、關(guān)稅政策等多種外部因素的影響。本文對國際棉花現(xiàn)貨價(jià)格的實(shí)證研究僅反映了國際棉花現(xiàn)貨價(jià)格短期內(nèi)的發(fā)展趨勢,暫不涉及國際棉花現(xiàn)貨價(jià)格的形成機(jī)制。自回歸移動平均模型(ARIMA)作為一種用于時(shí)間序列預(yù)測且精度較高的分析模型[8],能對短期內(nèi)國際棉花現(xiàn)貨價(jià)格的趨勢進(jìn)行較準(zhǔn)確的判斷,為我國棉花企業(yè)與植棉農(nóng)戶提供可參考的價(jià)格信息。

3.1 數(shù)據(jù)來源

本研究數(shù)據(jù)來源美國農(nóng)業(yè)部(USDA)數(shù)據(jù)庫公布的全球棉花價(jià)格相關(guān)數(shù)據(jù)(主要用于國際棉花價(jià)格的理論分析)和英國考特魯克(Cotlook)公司公布的全球棉花現(xiàn)貨價(jià)格指數(shù)(Cotlook FE-A)。

實(shí)證研究中使用的數(shù)據(jù)時(shí)間跨度為2004/2005—2015/2016年。一方面是由于我國于2002年正式加入世界貿(mào)易組織,國內(nèi)市場與國外市場的聯(lián)系逐步加強(qiáng),市場化進(jìn)程不斷加快;另一方面是由于2004年英國考特魯克公司開始發(fā)布世界棉花現(xiàn)貨價(jià)格指數(shù)(Cotlook FE-A,文中指國際棉花亞洲CIF到岸價(jià)指數(shù)),因此采用2004/2005—2015/2016年的數(shù)據(jù)作為分析數(shù)據(jù)。數(shù)據(jù)間隔為月度;使用的數(shù)據(jù)均由國際標(biāo)準(zhǔn)單位轉(zhuǎn)換為中國標(biāo)準(zhǔn)單位后的數(shù)據(jù),但由于匯率等因素導(dǎo)致數(shù)據(jù)與國內(nèi)相關(guān)數(shù)據(jù)存在不完全一致的可能性。

3.2 模型簡介

ARIMA模型最早是由博克思(Box)與詹金斯(Jenkins)提出[9],是分析與預(yù)測時(shí)間序列問題較成熟的模型。ARIMA模型以單個(gè)變量為研究對象,重點(diǎn)分析研究對象的變化規(guī)律,然后進(jìn)行預(yù)測。該模型共有三種形式,分別為自回歸模型(Autore-gressive Model)、移動平均模型(Moving Average Model)以及兩者的混合模型(ARMA),即自回歸移動平均模型。

AR(p)模型的表達(dá)式為:

Xt=c+a1Xt-1+a2Xt-2+…+apXt-p+εt

(1)

MA(q)模型的表達(dá)式為:

Xt=c+θ1εt-1+θ2εt-2+…+θqXt-q

(2)

ARMA(p,q)模型的表達(dá)式為:

Xt=c+a1Xt-1+a2Xt-2+…+apXt-p+εt+θ1εt-1+θ2εt-2+…+θqXt-q

(3)

ARMA模型建模主要分為以下四個(gè)步驟:一是由于ARMA要求序列必須是平穩(wěn)的,因此建模之前要對時(shí)間序列的平穩(wěn)性進(jìn)行檢驗(yàn)。若不平穩(wěn)，可通過差分法逐步消除線性趨勢直至平穩(wěn)。二是要對平穩(wěn)后的時(shí)間序列進(jìn)行ARMA模型的定階與參數(shù)估計(jì)。三是要檢驗(yàn)?zāi)Ｐ偷挠行浴Ｋ氖抢媚Ｐ瓦M(jìn)行預(yù)測,得到原時(shí)間序列的未來趨勢。

3.3 國際棉花現(xiàn)貨價(jià)格預(yù)測模型構(gòu)建

數(shù)據(jù)預(yù)處理:ARIMA模型的建立要求所分析的時(shí)間序列必須是平穩(wěn)的,因此首先需要對棉花價(jià)格時(shí)間序列(Xt)進(jìn)行平穩(wěn)性處理。根據(jù)判斷國際棉花價(jià)格時(shí)間序列圖,采用觀察法判斷原始時(shí)間序列是非平穩(wěn)的,整體具有明顯的線性趨勢。其次，運(yùn)用單位根(ADF)檢驗(yàn)法對原始序列進(jìn)行了檢驗(yàn),結(jié)果表明(表1)序列Xt的單位根T檢驗(yàn)統(tǒng)計(jì)量為-0.694673,在1%、5%、10%三種顯著性水平下,單位根檢驗(yàn)的臨界值分別為-2.580366、-1.942952、-1.615307。顯然,上述單位根的T檢驗(yàn)統(tǒng)計(jì)量明顯大于相應(yīng)的DW臨界值,說明序列Xt存在單位根,因此可斷定序列Xt是不平穩(wěn)的,需要進(jìn)行差分后使序列逐步到達(dá)平穩(wěn)。

表1 國際棉花現(xiàn)貨價(jià)格序列單位根(ADF)檢驗(yàn)

對原始序列Xt進(jìn)行一階差分得到序列DXt,并做該序列的1階差分圖(圖2),一階差分后的時(shí)間序列基本均勻分布在0刻度線上下兩側(cè),因此可從序列圖中初步認(rèn)為一階差分序列是平穩(wěn)的。為了保證檢驗(yàn)的科學(xué)有效性,再對序列DXt進(jìn)行上述單位根(ADF)檢驗(yàn)(表2),其中DXt序列的單位根T檢驗(yàn)統(tǒng)計(jì)量為-8.724729,在1%、5%、10%三種顯著性水平下,DXt序列的單位根檢驗(yàn)的臨界值分別為-3.473967、-2.880591、-2.577008。顯然,上述單位根的T檢驗(yàn)統(tǒng)計(jì)量明顯小于相應(yīng)的DW臨界值,說明序列DXt不存在單位根,因此可判定序列DXt是平穩(wěn)序列,能滿足ARIMA模型的建模需要。

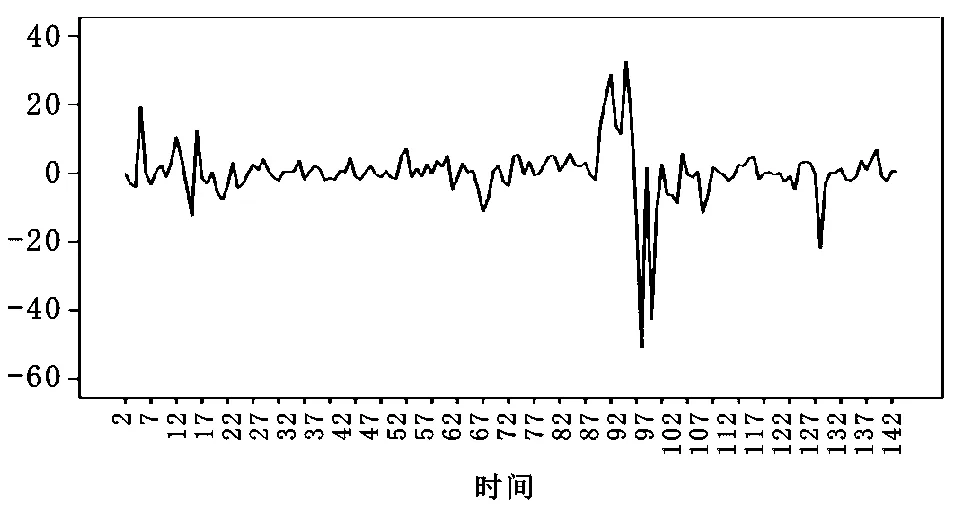
圖2 國際棉花現(xiàn)貨價(jià)格一階差分序列

表2 國際棉花現(xiàn)貨價(jià)格一階差分序列單位根(ADF)檢驗(yàn)

模型識別:對Xt序列進(jìn)行一階差分后得到平穩(wěn)的DXt序列,因此可確定ARIMA(p,d,q)模型中d為1。模型中p與q一般通過一階差分序列圖和表來確定。根據(jù)表3,殘差自相關(guān)在滯后4期后趨于0但不都等于0,可取p(1,4),結(jié)合1階差分序列自相關(guān)圖(圖3)中殘差延遲次數(shù)為2時(shí)的殘差趨于0,因此選擇p=2;殘差偏自相關(guān)在滯后3期后趨于0但不都為0,因此q可取(1,3),結(jié)合一階差分序列偏自相關(guān)圖(圖3)中殘差延遲次數(shù)為3時(shí)的殘差趨于0,因此確定q=3。初步確定p=2、d=1、q=3為ARIMA的最優(yōu)形式后對ARIMA(2,1,3)進(jìn)行參數(shù)估計(jì),結(jié)果見表4。AR(1)、AR(2)、MA(1)、MA(2)、MA(3)的參數(shù)在5%的置信區(qū)間內(nèi)顯著不小于0。調(diào)整的R2達(dá)到0.939,說明序列93.9%都可通過ARIMA(2,1,3)進(jìn)行說明。模型的解釋能力較良好,將各模型參數(shù)帶入式(3),最終得到ARIMA(2,1,3)模型的表達(dá)式為:

Xt=0.808+1.602Xt-1-0.650Xt-2+εt+1.355εt-1-0.401εt-2+0.0401Xt-3

(4)

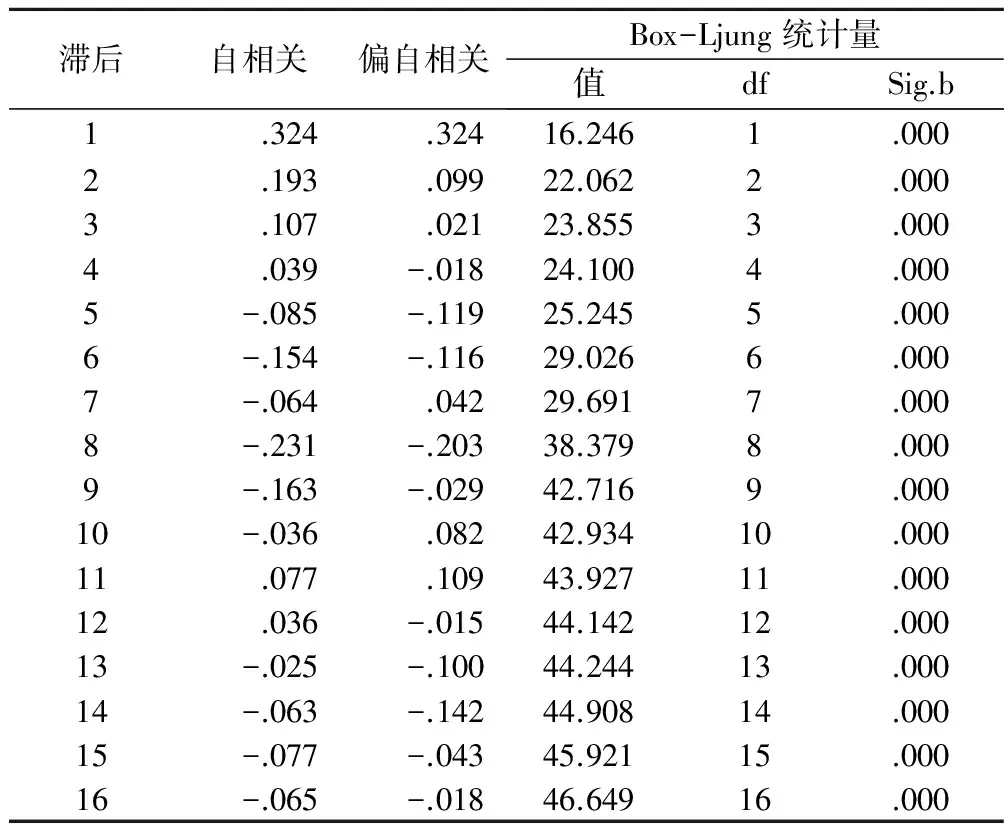
表3 國際棉花現(xiàn)貨價(jià)格一階差分序列自(偏)相關(guān)狀況

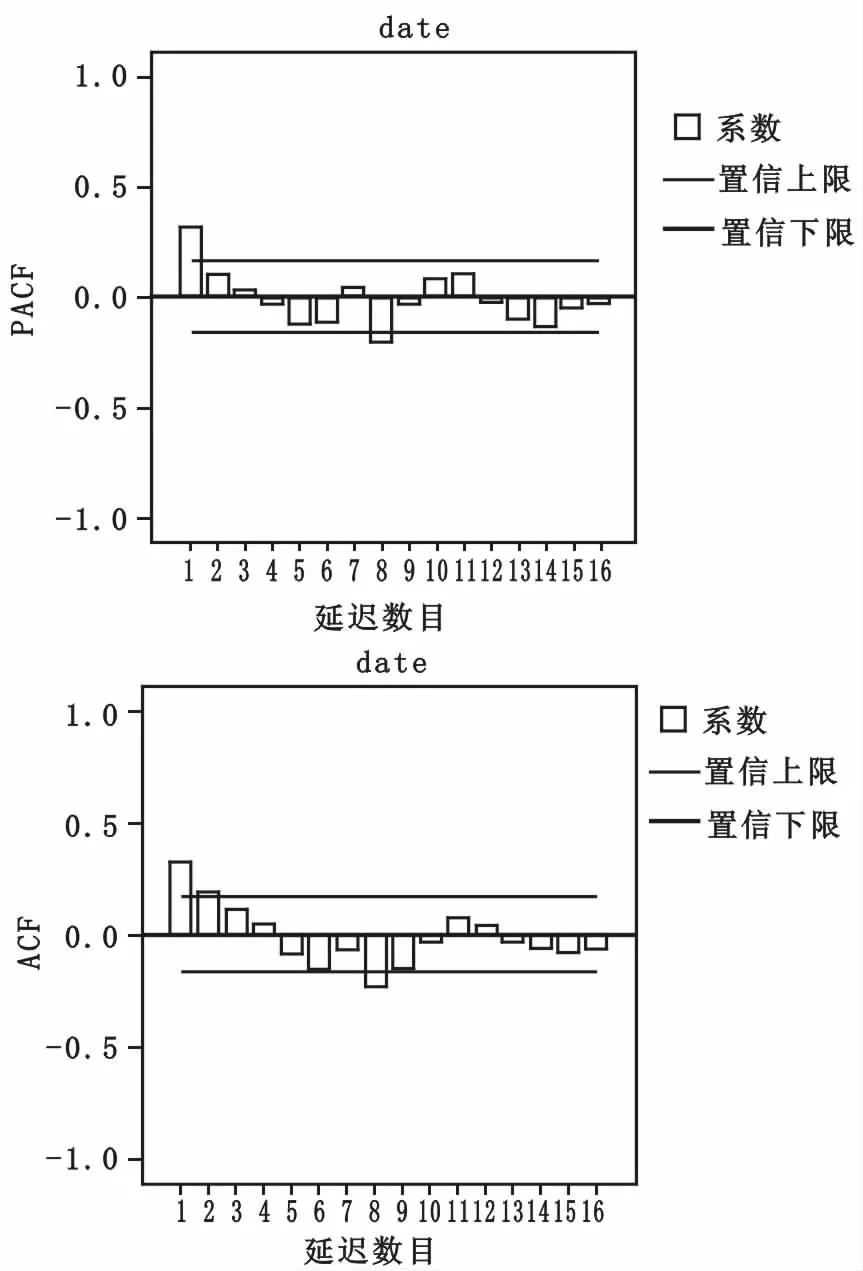
圖3 國際棉花現(xiàn)貨價(jià)格一階差分序列自(偏)相關(guān)狀況

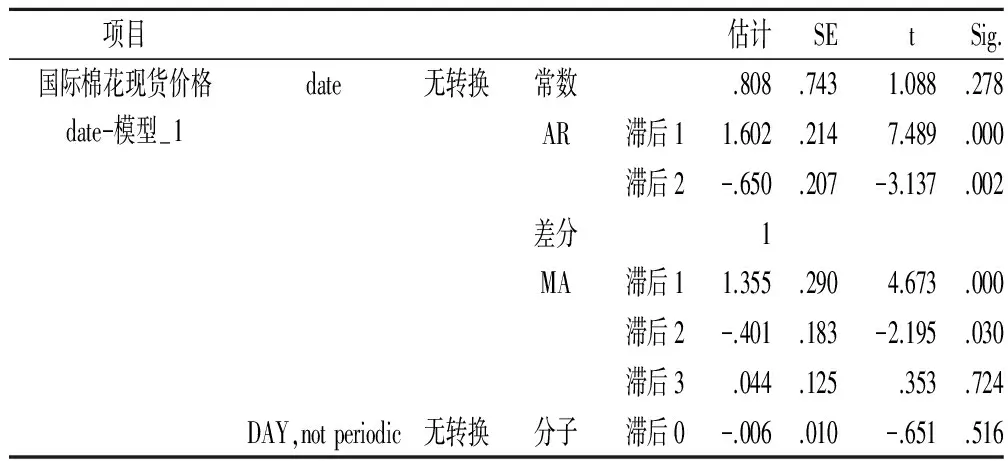
表4 模型參數(shù)估計(jì)

模型檢驗(yàn):確定國際棉花現(xiàn)貨價(jià)格ARIMA(2,1,3)模型后,必須對該模型進(jìn)行檢驗(yàn),確定模型殘差序列的自相關(guān)與偏相關(guān)系數(shù)是否落入隨機(jī)區(qū)間后才能根據(jù)模型進(jìn)行預(yù)測。因此,對模型殘差序列進(jìn)行圖4的自相關(guān)圖與偏相關(guān)圖。從圖4可明顯看出，殘差自相關(guān)系數(shù)與殘差偏自相關(guān)系數(shù)均未出現(xiàn)拖尾或截尾的情況,系數(shù)均落在隨機(jī)區(qū)間以內(nèi),表明模型正確可靠,能對原始序列進(jìn)行良好的擬合。殘差序列的自相關(guān)函數(shù)均在95%的置信區(qū)間內(nèi),因此不拒絕原假設(shè),模型的殘差序列不存在自相關(guān),近似于白噪聲序列,能顯著對變量進(jìn)行模擬,且模型效果良好(圖5)。

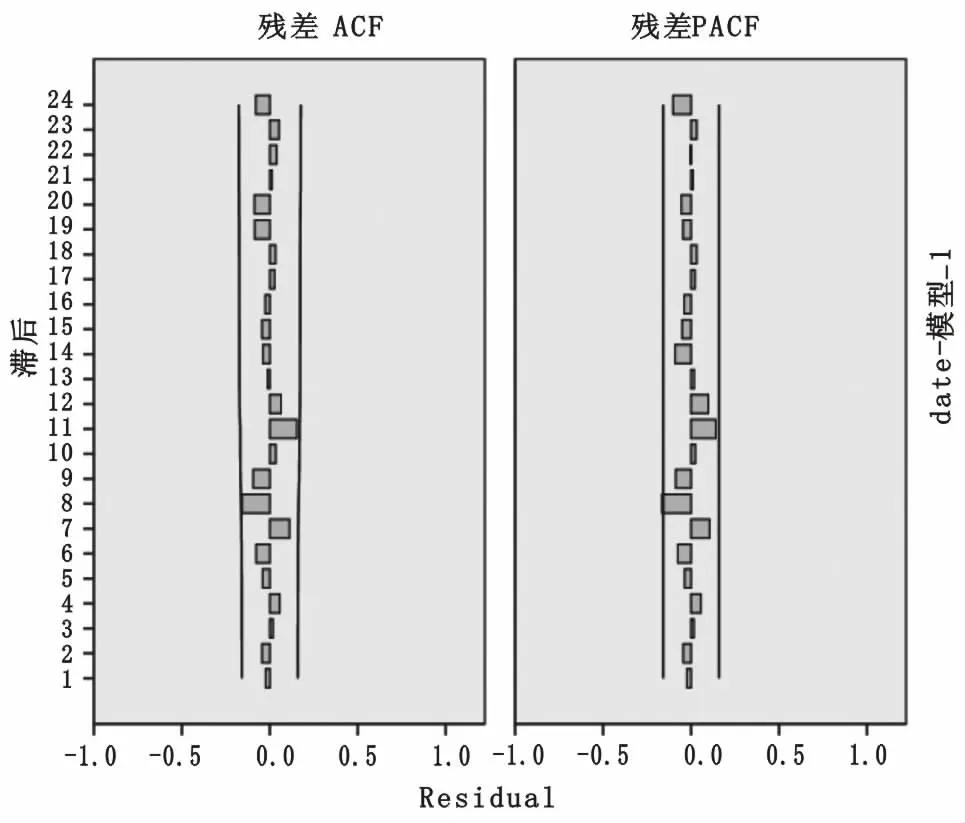
圖4 模型殘差序列的自(偏)相關(guān)狀況

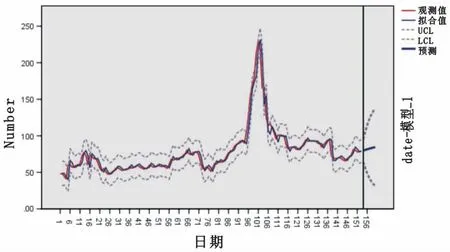
圖5 模型擬合

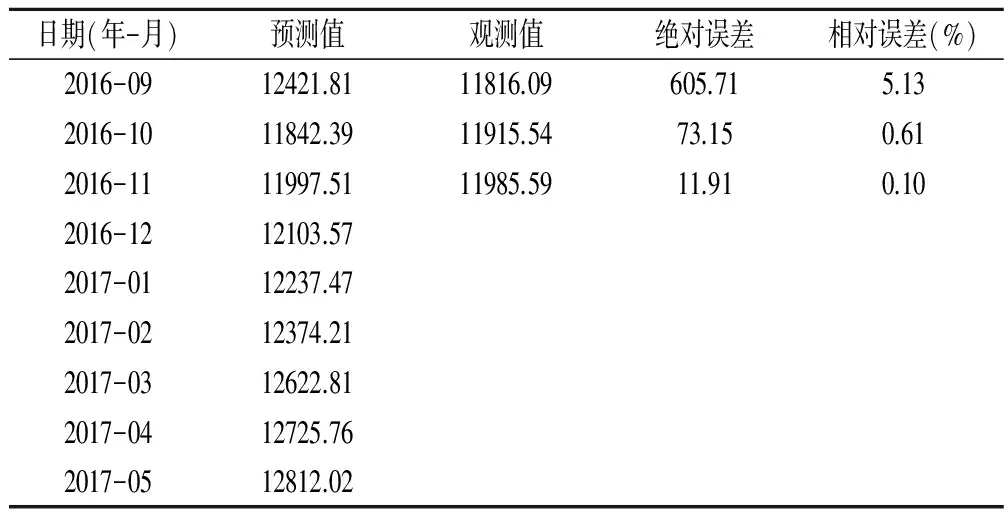
表5 國際棉花現(xiàn)貨價(jià)格短期預(yù)測單位(元/t)

3.4 預(yù)測

利用ARMA(2,1,3)模型對國際棉花現(xiàn)貨價(jià)格進(jìn)行模擬與預(yù)測,模型的平均誤差為1.95%,說明模型的誤差較小,能較精確地對序列進(jìn)行預(yù)測。2016年12月國際棉花現(xiàn)貨價(jià)格較11月份有所上升,但增幅僅有1%,達(dá)到12103.57元/t;2017年1月—5月國際棉花現(xiàn)貨價(jià)格呈緩慢上升的趨勢,分別達(dá)到12237.47元/t、12504.56元/t、12622.81元/t、12725.76元/t、12812.02元/t(以2016年12月1日美元兌人民幣匯率為準(zhǔn)進(jìn)行換算),表明在未來短期內(nèi)國際棉花現(xiàn)貨價(jià)格呈現(xiàn)出小幅上漲的趨勢(表5)。

4 結(jié)論與討論

2004/2005年至今,國際棉花價(jià)格經(jīng)歷了“大起大落”的劇烈波動，特別是全球經(jīng)濟(jì)危機(jī)以來,全球經(jīng)濟(jì)發(fā)展疲軟、棉花消費(fèi)市場萎縮、國際棉花現(xiàn)貨價(jià)格大幅下降,導(dǎo)致我國依靠國外市場的出口型紡織企業(yè)大量減產(chǎn)、停產(chǎn)和瀕臨破產(chǎn),同時(shí)棉花價(jià)格下降給植棉農(nóng)戶造成了重大的損失,2013/2014年以來國際棉花現(xiàn)貨價(jià)格再一次呈現(xiàn)出持續(xù)降低的趨勢。

通過ARIMA模型對國際棉花現(xiàn)貨價(jià)格的預(yù)測結(jié)果來看,短期內(nèi)國際棉花現(xiàn)貨價(jià)格呈現(xiàn)出緩慢回升的趨勢,2016/2017年1月國際棉花現(xiàn)貨價(jià)格將回升到12237.47元/t,但要上漲到2011/2012年的高位水平有較大差離。2016/2017年5月國際棉花現(xiàn)貨價(jià)格將上升為12812.02元/t,較2016年12月增幅達(dá)到688.83元/t。我國棉花現(xiàn)貨價(jià)格易受國際棉花現(xiàn)貨價(jià)格波動影響的主要原因集中在我國棉花國際現(xiàn)貨價(jià)格制定權(quán)缺失與風(fēng)險(xiǎn)應(yīng)對措施單調(diào)等兩個(gè)方面,因此當(dāng)前在國際棉花價(jià)格緩慢上漲、國際棉花需求逐漸回升的國際棉花市場趨勢下,保障我國棉花市場的穩(wěn)定與可持續(xù)發(fā)展是十分重要的。

我們認(rèn)為:①增強(qiáng)中國棉花的國際競爭力,積極謀求國際棉花價(jià)格定價(jià)權(quán)。我國棉花缺失國際棉花現(xiàn)貨價(jià)格的定價(jià)權(quán),只能被動接受國際棉花現(xiàn)貨價(jià)格,究其原因是因?yàn)槲覈藁ǜ偁幜Σ蛔恪Ｒ虼?一方面應(yīng)在穩(wěn)定棉花產(chǎn)量的前提下著重提升我國棉花品質(zhì),加大對棉花種子資源的培育與實(shí)驗(yàn),提升我國棉花的纖維長度與韌性,逐步優(yōu)化我國棉花種植區(qū)域,大膽淘汰“不宜棉區(qū)”與“次宜棉區(qū)”,加大對“適宜棉區(qū)”的扶持力度;另一方面應(yīng)積極更新棉花采摘與加工技術(shù)[10],減少棉花在機(jī)械采摘、加工過程中的受損程度,從而提升我國棉花的品質(zhì),在國際棉花市場競爭中取得質(zhì)的優(yōu)勢,扭轉(zhuǎn)國內(nèi)棉花企業(yè)大力購買高品質(zhì)外國棉花的趨勢,逐步建立以中國為中心的世界棉花生產(chǎn)—貿(mào)易格局,增強(qiáng)中國棉花的國際競爭力和國際棉花現(xiàn)貨價(jià)格的定價(jià)話語權(quán)。②合理規(guī)避棉花現(xiàn)貨風(fēng)險(xiǎn),實(shí)現(xiàn)棉花市場“兩條腿走路”。一方面，應(yīng)加強(qiáng)對世界棉花市場形勢的研究與判斷,正確引導(dǎo)植棉農(nóng)戶的棉花生產(chǎn)行為,防范植棉農(nóng)戶因國際棉花價(jià)格的短期上漲盲目擴(kuò)大棉花種植面積,造成供大于求,“谷賤傷農(nóng)”的現(xiàn)象;另一方面，由于國內(nèi)企業(yè)大量使用“物美價(jià)廉”的國外棉花，導(dǎo)致我國用棉企業(yè)對外棉的依賴逐漸增強(qiáng),增大了國內(nèi)棉花市場受國際棉花價(jià)格波動沖擊的可能性。因此,在棉花企業(yè)生產(chǎn)活動中要合理配置國內(nèi)外資源,減少對國外棉花的依賴,削弱國際棉花現(xiàn)貨風(fēng)險(xiǎn)的影響。此外,由于當(dāng)前我國棉花市場仍然以現(xiàn)貨交易為主,缺乏及時(shí)預(yù)測與規(guī)避國際棉花現(xiàn)貨價(jià)格波動影響的手段，因此國際棉花現(xiàn)貨價(jià)格波動對我國棉花價(jià)格產(chǎn)生了較大的不利影響。根據(jù)棉花期貨貿(mào)易價(jià)格發(fā)現(xiàn),套期保值等功能作為規(guī)避現(xiàn)貨市場風(fēng)險(xiǎn)和套期保值的工具在國外的應(yīng)用已十分普遍和成熟,因此應(yīng)大力建設(shè)中國棉花期貨市場,積極將中國棉花相關(guān)主體積極引入到棉花期貨市場中,豐富棉花期貨產(chǎn)品,將棉花保險(xiǎn)與棉花期貨相結(jié)合,實(shí)現(xiàn)新型的棉花價(jià)格保障機(jī)制,從而實(shí)現(xiàn)現(xiàn)貨市場與期貨市場“兩條腿”走路,合理規(guī)避國際棉花現(xiàn)貨價(jià)格波動對我國棉花價(jià)格造成的不利影響。

[1]楊蓮娜,田秀華.國際棉花生產(chǎn)及貿(mào)易格局分析[J].中國棉花加工,2014,(1)∶34-38.

[2]喻樹迅.我國棉花生產(chǎn)現(xiàn)狀與發(fā)展趨勢[J].中國工程科學(xué),2013,(4)∶9-13.

[3]譚硯文,關(guān)建波.宏觀經(jīng)濟(jì)因素、消費(fèi)需求、市場信息與棉花市場價(jià)格波動[J].農(nóng)業(yè)技術(shù)經(jīng)濟(jì),2013,(8)∶12-22.

[4]賈兆祥.棉花消費(fèi)、庫存對世界棉花生產(chǎn)的影響——基于1971—2011年的實(shí)證檢驗(yàn)[J].世界農(nóng)業(yè),2013,(11)∶101-104.

[5]李琴,孫良媛.棉花價(jià)格、進(jìn)口及庫存的互動關(guān)系[J].中國農(nóng)村經(jīng)濟(jì),2005,(7)∶71-77.

[6]羅英姿,王凱.中國棉花生產(chǎn)成本分析及國際比較[J].農(nóng)業(yè)技術(shù)經(jīng)濟(jì),2003,(4)∶36-40.

[7]王兆陽,辛賢.大國開放條件下棉花市場價(jià)格決定研究[J].中國農(nóng)村觀察,2004,(3)∶35-43,80.

[8]張立杰,朱新杰.我國棉花價(jià)格長期走勢與短期預(yù)測——基于差分自回歸移動平均模型(ARIMA)的分[J].價(jià)格理論與實(shí)踐,2012,(6)∶53-54.

[9]薛冬梅.ARIMA模型及其在時(shí)間序列分析中的應(yīng)用[J].吉林化工學(xué)院學(xué)報(bào),2010,(3)∶80-83.

[10]李勤昌,昌敏.提升中國棉花產(chǎn)業(yè)國際競爭力的路徑選擇[J].國際貿(mào)易問題,2011,(10)∶34.

StudyonFluctuationofInternationalCottonSpotPriceandShortTermPrediction

YAN Qing-hua,LIU Wei-zhong,QIN Zi
(School of Economics and Business,Xinjiang Agricultural University,Urumqi 830052,China)

With the deepening of China′s market-oriented reform of cotton,the relationship between China′s cotton market and the international cotton market was becoming more and more closely.From 2004/2005 to 2015/2016 international cotton spot price (Cotlook FE-A)monthly data on the basis of theoretical analysis,this paper theoretically analyzed the fluctuations of international cotton spot price,then applied the ARIMA model to predict the fluctuation trend of international cotton spot price in the short term,the model relative error was below 5%,the predictive value of precision was high.Model prediction results showed that in the short term the international cotton spot prices showed a slow upward trend in May 2017 which wouldl rise to 12812.02yuan/t,an increase of up to 688.83yuan/t than December 2016.Based on the fluctuation trend of the international cotton spot price,this paper put forward some countermeasures and suggestions to prevent the impact of international cotton price fluctuation and ensure the sustainable development of China′s cotton industry.

ARIMA model;international cotton price;price forecasting;short-term trend

10.3969/j.issn.1005-8141.2017.05.013

F323.7

A

1005-8141(2017)05-0575-04

2017-03-27；

2017-04-15

國家社科基金青年項(xiàng)目(編號:16cjy023);自治區(qū)級研究生產(chǎn)學(xué)研聯(lián)合培養(yǎng)項(xiàng)目(編號:xjaucxy-yjs-20141020);新疆人文社科重點(diǎn)研究基地干旱區(qū)農(nóng)村發(fā)展研究中心資助。

閆慶華(1991-),男,安徽省阜陽人,碩士研究生,研究方向?yàn)楝F(xiàn)代農(nóng)業(yè)發(fā)展與政策、農(nóng)產(chǎn)品貿(mào)易等。

劉維忠(1961-),男,新疆維吾爾自治區(qū)哈密人,教授,博士生導(dǎo)師,研究方向?yàn)檗r(nóng)業(yè)經(jīng)濟(jì)管理政策、財(cái)務(wù)管理等。