慣性輔助高動態RTK模糊度浮點解求解算法研究

高亞豪，左啟耀，鄒志勤，李 峰，胡文濤

(北京自動化控制設備研究所，北京100074)

慣性輔助高動態RTK模糊度浮點解求解算法研究

高亞豪，左啟耀，鄒志勤，李 峰，胡文濤

(北京自動化控制設備研究所，北京100074)

載波相位差分(RTK)技術需要著重解決整周模糊度快速精確求解問題。針對高動態應用，提出一種利用慣性信息輔助求解RTK整周模糊度浮點解的算法，建立了基于加速度信息輔助的Kalman濾波器模型，分析了加速度誤差和慣導信息延遲對濾波結果的影響，并通過仿真對算法的動態性能進行了深入研究。仿真結果表明，與未受輔助的Kalman濾波算法相比，基于慣性輔助的求解算法能夠在高動態下獲得較精確的整周模糊度浮點解，使后續整數解的搜索空間更小，提升了模糊度固定效率和成功率；在發生周跳、出現野值和跟蹤到新衛星信號的情況下，該算法同樣具有很好的模糊度浮點解求解性能；此外，慣導加速度的隨機測量誤差和信息延遲不會對算法的性能造成較大影響。

慣性輔助；RTK；整周模糊度；Kalman濾波；高動態

0 引言

基于載波相位的動態差分(RTK)技術的關鍵是整周模糊度的快速準確求解。模糊度的實數估計是模糊度解算的第一步，它為模糊度參數提供一個搜索初始值，通常情況下是浮點數。高精度的模糊度浮點解，能夠減小整數搜索空間，有助于提高模糊度固定的成功率和效率。

常用的模糊度浮點解求解方法有最小二乘法和Kalman濾波法。最小二乘法很難實現單歷元解算，而利用多歷元數據會增加矩陣維數，計算量大大增加，并且存在方程病態的問題。對于Kalman濾波法，由于機動載體的運動復雜多變，系統模型很難準確建立。當載體實際的運動狀態與濾波器的動態模型不相符時，容易造成發散。針對這一問題，一些學者提出了一階時間相關模型(Singer模型)、當前統計模型等動態模型[7]，用以提高濾波器的動態適應性，但仍然無法從根本上解決濾波發散問題。

可見，僅利用自身測得的雙差觀測量難以在動態下獲得精度較高的整周模糊度浮點解。而慣性導航系統(INS)具有完全自主、實時性好等優點，能夠為差分定位系統提供精度較高的位置和姿態信息。國內外在利用慣性信息輔助求解整周模糊度的領域已取得許多研究成果：1999年，Jan Skaloud提出利用INS信息輔助整周模糊度搜索，從而減小了整數搜索空間，提高了固定成功率；2010年，劉景瑞分別利用INS的航向角信息和位置信息輔助求解整周模糊度，改善了方程狀態，提高了模糊度浮點解精度，并通過實驗分析了慣導位置精度對模糊度搜索的影響[2]；2013年，謝宏飛等分析了在松組合和緊組合兩種INS/GPS組合模式下，慣導位置精度對模糊度解算的影響，得出了緊組合模式下INS輔助效果明顯優于松組合模式的結論[6]。但這些研究主要集中在利用慣導系統輸出的位置信息進行輔助，而慣導的位置信息具有誤差隨時間累積的缺點，難以取得較好的輔助效果。

針對上述問題，本文提出一種直接利用慣導系統的加速度測量值輔助解算模糊度的Kalman濾波算法。由于加速度信息的輔助，算法模型中不再需要對載體動態特性建模，避免了模型不準確帶來的發散現象，從而很好地解決了高動態求解問題。此外，本文深入分析了加速度的測量誤差和延時誤差對浮點解的影響，最后通過仿真對算法在高動態下的性能進行了驗證。

1 慣性信息輔助的模糊度求解算法

在求解整周模糊度浮點解的Kalman濾波模型中，系統的狀態向量中除了包含接收機天線的位置和速度參數外，還將整周模糊度作為狀態向量的一部分，通過偽距、載波相位雙差觀測值進行濾波估計，得到接收機天線的位置、速度以及模糊度浮點解。

設待估計的狀態向量x為

x=(r,v,N1,N2)T

(1)

在等速模型的基礎上，將慣導系統輸出的加速度a作為濾波器狀態轉移函數的輸入量，則位置和速度對應的狀態轉移函數可以寫為

(2)

式中，I為3×3的單位陣，ts為2個觀測歷元之間的時間間隔，ak表示慣導系統在歷元k獲得的加速度測量值。

單差模糊度參數的狀態轉移過程與衛星的升降變化及信號跟蹤情況有關，需要根據具體的衛星變化情況進行處理，這種處理一般都是非線性的。

系統的過程噪聲協方差矩陣可設為對角陣，其對角線元素的大小根據實際載體的運動狀態確定。若載體機動頻繁或運動過程中受到較大外界干擾，協方差矩陣的對角線元素應設置大一些，否則應設置較小。

設系統的觀測向量y為

y=(φ1,φ2,p1,p2)T

(3)

根據雙差載波相位和雙差偽距的觀測方程，可得系統的觀測函數為

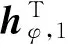
(4)

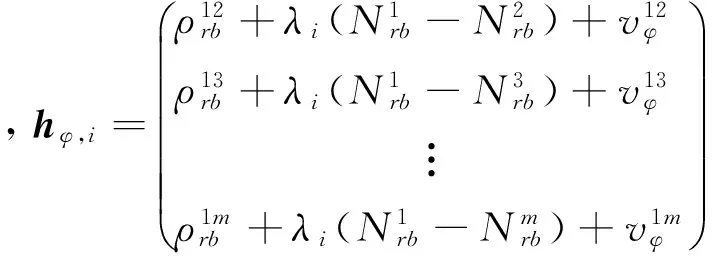
其對應的觀測噪聲協方差矩陣R為

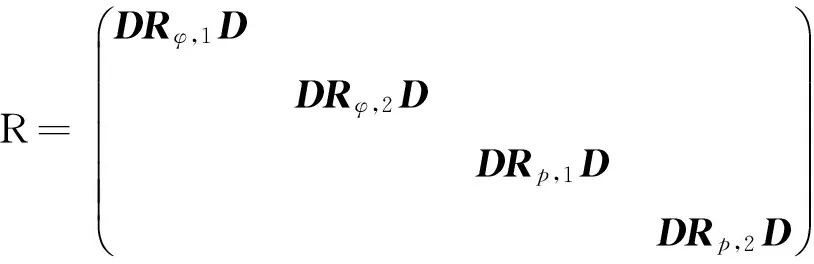
(5)

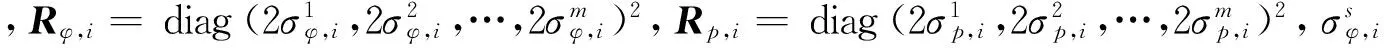
由于狀態轉移函數和觀測函數都是非線性函數，本文采用擴展Kalman濾波算法計算各個時刻的參數估計值。

加速度測量值的輔助為濾波算法提供了載體運動的先驗信息，簡化了濾波器的動態模型，從而減小了計算的復雜度。在動態差分定位中，由于周跳、失鎖、跟蹤到新的衛星信號等情況需要固定整周模糊度時，該濾波算法能夠實時給出當前歷元估計出的模糊度浮點解及其協方差矩陣，即可用于整數搜索，不需要重新解算雙差觀測方程。

2 加速度精度對濾波結果的影響分析

慣導系統測得的載體加速度不可避免地存在誤差。由于加速度是濾波器的輸入量，加速度誤差可以看作是濾波器的模型誤差。下面分析加速度誤差對濾波估計結果的影響。

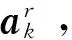
(6)

而現實濾波得到的參數估計值為

(7)

因此，參數估計的差值為

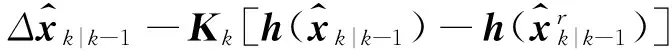
(8)

其中

(9)

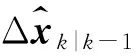
(10)

(11)

因此，式(8)和式(9)可相應轉換為

(12)

(13)

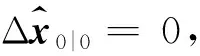
將式(13)代入式(12)，并取期望得

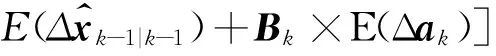
(14)

在實際的導航應用中，若慣導系統與差分定位系統的采樣時間不重疊，或者信息傳輸速率有限，則可能出現加速度信息的延遲。這種情況下，當載體的加速度變化時，加速度誤差不再是一個均值為0的白噪聲，并且這種偏差將會對后續的濾波結果產生影響。但本文通過仿真證明，只要將加速度延遲控制在合理范圍內，就不會使濾波結果出現較大偏差，并且這部分偏差可以通過后續的濾波作用逐漸減小甚至消除，不會影響模糊度的正確求解。仿真結果見3.4節中所述。

由式(14)可知，為了減小加速度延遲造成的濾波偏差，需要減小矩陣Fk-1和Bk中元素的絕對值。通過增加采樣率，縮短每個歷元間的時間間隔，即可達到上述目的，從而減小信息延遲的影響。

3 仿真驗證

3.1 仿真場景

為了驗證新算法的性能，設計了高動態仿真場景，通過Matlab軟件模擬高動態載體(如某高速飛行器等)的運動，計算出差分定位所需的各時刻的偽距和載波相位觀測量。

仿真場景設定為：時間從2012年4月18日13時2分0秒到當日的13時3分39.8秒，歷元間間隔為0.2s，共500個歷元。基準站坐標為東經116.1528813°，北緯39.8121276°，高程74.48m，流動站的初始坐標為東經116.1563849°，北緯39.8112269°，高程74.49m。在13時2分0秒時流動站的初速度為1600m/s，方向向西，加速度和加加速度均為0；前20s，流動站的加加速度為8m/s3，方向向東；第20s到第30s流動站的加加速度變為0，做加速度為160m/s2方向向東的勻加速運動；從第30s開始，流動站處于勻速運動狀態，速度為1600m/s，方向向東，直至場景結束。

觀測噪聲為均值為0的高斯白噪聲，其中偽距觀測量噪聲的標準差為0.5m，載波相位觀測量噪聲的標準差為0.006m，仿真中只使用GPS的L1頻點的觀測量。偽距和載波相位觀測量均不包含接收機鐘差、衛星鐘差、電離層延遲、對流層延遲等誤差，這些誤差在中短基線的雙差模型中基本都可以抵消。

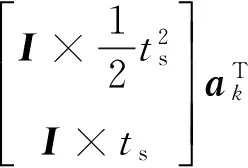
3.2 動態性能分析

算法I和算法II的位置誤差曲線如圖1所示，速度誤差曲線如圖2所示，模糊度浮點解誤差曲線如圖3所示。

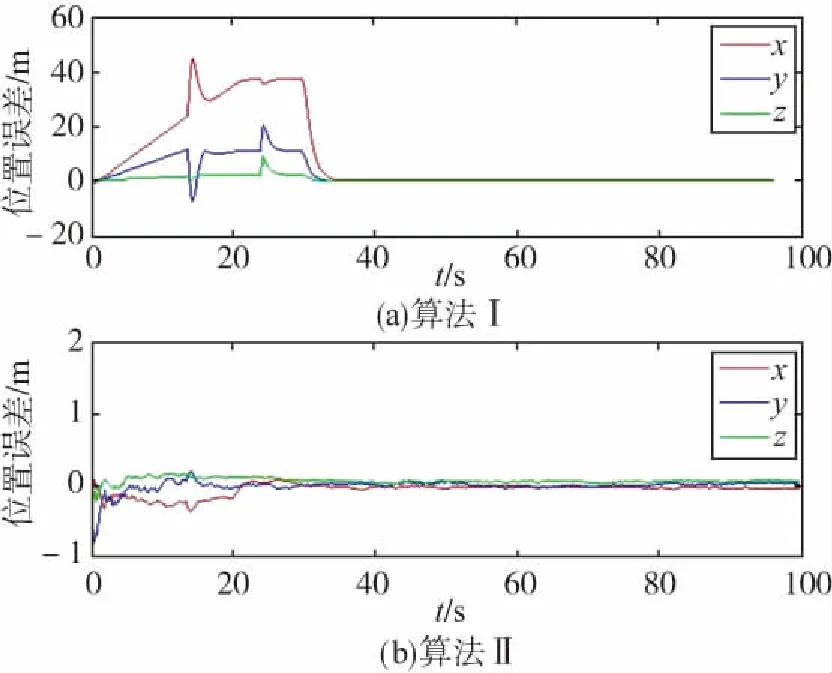
圖1 位置誤差曲線Fig.1 Position error curve

圖2 速度誤差曲線Fig.2 Velocity error curve

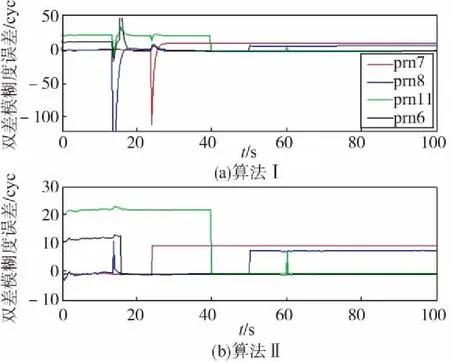
圖3 雙差模糊度誤差曲線Fig.3 Double difference ambiguity error curve

圖1和圖2中，x、y、z方向分別表示WGS-84坐標系下的3個坐標軸的正向，與狀態向量中的位置和速度參數表示的含義相同。在前30s加速度不為0時，采用等速模型的Kalman濾波器(算法I)無法得到正確的位置和速度估計值，它們與真值都有很大的偏差。而慣性輔助的濾波器(算法II)可以得到精度較高的位置和速度，其誤差只受加加速度影響。當載體的加加速度為0時，無論加速度有多大，估計值的精度都與勻速運動相同。這說明，通過將慣導系統的加速度信息輸入到濾波器中，算法的動態性能得到了極大的提升。

圖3中的4條曲線分別表示衛星號為6、7、8、11的衛星與19號衛星組成的雙差模糊度。根據仿真場景設定，基準站在第16s和第40s才分別跟蹤到6號衛星和11號衛星。在這2個時刻之前，它們對應的單差模糊度參數為0，此時圖中曲線表示的是參考星單差模糊度的相對變化情況，沒有實際意義。當獲得它們的觀測量后，曲線才表示對應衛星的雙差模糊度。因此，從這2個時刻開始，6號衛星和11號衛星的模糊度曲線才分別開始向真值收斂。第16s，算法I中的6號衛星模糊度發生了大跳變，然后才逐漸向真值收斂。而對于算法II，6號衛星在此時可以迅速得到精度較高的浮點解。

根據仿真場景設定，8號衛星和11號衛星的載波相位觀測值分別在第14s和第60s出現了野值；第24s，7號衛星出現了大小為10周的周跳；第50s，8號衛星出現了大小為8周的周跳。當某顆衛星發生周跳后，它的模糊度誤差曲線應收斂到其周跳的周數。因此，第24s后7號衛星的模糊度誤差曲線最終收斂到10，第50s后8號衛星的模糊度誤差曲線最終收斂到8。前30s內，算法II在出現野值和周跳后，相應的模糊度參數都可以快速收斂到真值附近，不會出現算法I中的大跳變。

以上結果表明，當高動態環境下出現觀測量異常時，即跟蹤到新衛星信號、出現野值或發生周跳時，慣性輔助的濾波器仍然可以正常濾波，且收斂速度快。需要說明的是，濾波改善效果僅在加速度不為0時能夠明顯體現出來，而當載體作勻速運動時，一般的Kalman濾波器也能夠正常濾波。慣性輔助的算法在復雜動態環境中具有明顯優勢。

3.3 輔助算法對模糊度固定的改善

當仿真場景中所有衛星都正常跟蹤時，考察兩種濾波算法得到的模糊度浮點解及其協方差矩陣對模糊度固定的影響。

對濾波得到的每個歷元的浮點解及其協方差矩陣采用LAMBDA算法進行降相關變換和整數搜索，分別統計兩種算法對應的整數搜索時間和固定成功率如表1所示。

表1 兩種算法的模糊度固定結果Tab.1 The results of fixing ambiguities oftwo kinds of algorithm

表1中的成功率是用模糊度搜索成功的歷元數除以總歷元數得到的，其中總歷元數包括濾波器未收斂時的歷元，因此該成功率并不是接近100%，而濾波器收斂后即可固定成功。表1中的平均搜索時間是指Matlab軟件在每個歷元執行整數搜索程序所用時間的算術平均值。模糊度搜索采用的是橢球空間逐步縮小的方法，初始的搜索空間為無窮大，無需人為設定。因此，整數搜索時間與搜索參數設置無關。

兩種算法每個歷元的搜索時間如圖4所示。

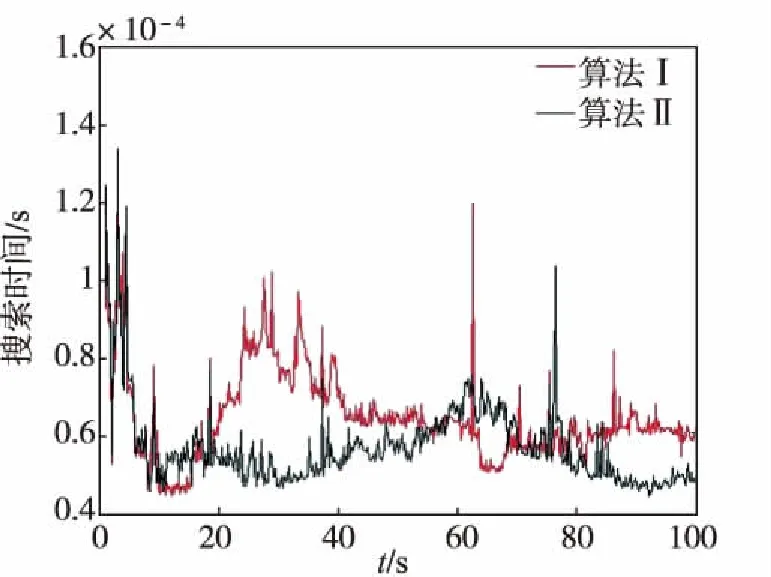
圖4 兩種算法的搜索時間曲線Fig.4 The searching time curve of two algorithms

固定成功率反映了模糊度解的有效性，而整數搜索時間能夠直接反映搜索的效率。可見，算法II在固定成功率和搜索效率上都明顯優于算法I。從圖4中可以看出，在加速度較大時，2個算法對應的搜索時間差別較大；當加速度變為0后，搜索時間的差別逐漸減小。

上述結果證明，加速度輔助的Kalman濾波器在復雜動態條件下提高了模糊度浮點解的精度，對模糊度固定具有明顯改善作用：一方面提高了固定成功率，增加了模糊度解的可靠性；另一方面縮小了搜索空間，使得整數搜索時間減少，提高了解算效率。

3.4 加速度誤差和延遲的影響分析

利用3.2節中的仿真場景，在不存在加速度信息延遲的情況下，對慣導的加速度添加不同大小的隨機誤差，其仿真結果如圖5所示。

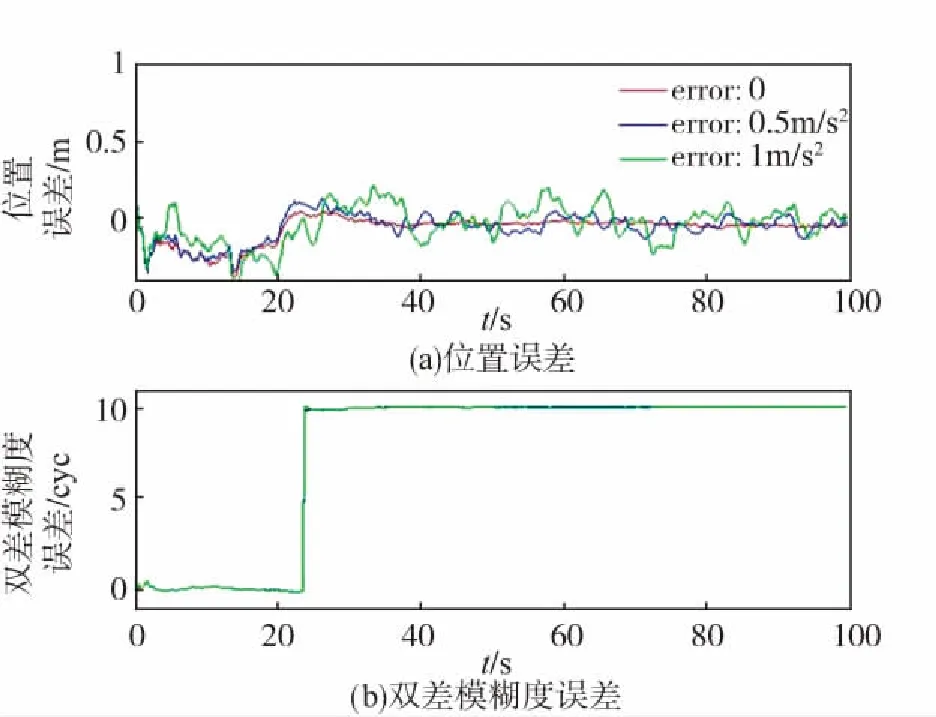
圖5 加速度誤差大小對濾波結果的影響Fig.5 The influence of acceleration error on the filter results

圖5(a)表示流動站x坐標分量的誤差大小變化曲線，圖5(b)表示7號衛星的雙差模糊度浮點解誤差曲線，其含義與圖3相同。圖中3條曲線對應的加速度隨機誤差標準差分別為0m/s2、0.5m/s2和1m/s2。可見，當用于輔助解算的加速度含有隨機測量誤差且不存在信息延遲時，濾波得到的位置誤差在0附近上下波動，波動的大小與加速度誤差呈正相關；當存在加速度誤差時模糊度參數仍然能夠快速收斂，不受加速度誤差大小的影響。因此，可以證明這種濾波估計是無偏的。

下面利用3.2節中的仿真場景對加速度延遲的影響進行仿真分析。設加速度的隨機測量誤差的標準差為0.1m/s2，在加速度分別延遲0s、20ms和50ms的情況下，對算法進行了仿真，仿真結果如圖6所示。

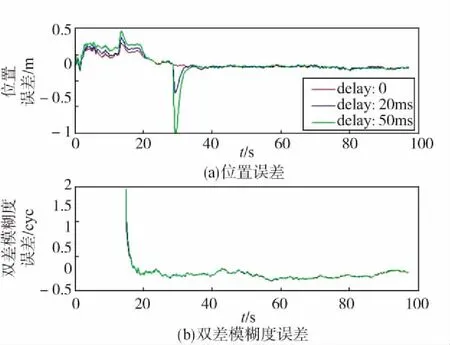
圖6 加速度延遲對濾波結果的影響Fig.6 The influence of acceleration delay on the filter results

圖6(a)表示流動站x坐標分量的誤差大小變化曲線，圖6(b)表示6號衛星的雙差模糊度浮點解誤差曲線，其含義與圖3相同。從上述結果中可以發現，只有當流動站的加速度變化時，加速度信息的延遲才會對濾波結果產生影響，并且延遲越大，濾波結果的誤差越大。當加速度趨于穩定時，誤差逐漸減小，消除了加速度延遲帶來的影響。第30s加速度從160m/s2突變為0，慣導加速度信息的延遲使得濾波結果出現較大誤差，而之后該誤差迅速收斂到0。可以看出，加速度延遲對動態模型造成的誤差可以通過濾波作用消除，不會對后續結果產生影響。此外，加速度延遲對模糊度參數的收斂速度影響很小，沒有導致算法動態性能的下降。

4 結論

本文主要研究了慣性信息輔助求解整周模糊度浮點解的Kalman濾波算法。由于慣性信息的輔助，Kalman濾波器的動態性能有了明顯提高，并通過理論分析和仿真證明，在一定條件下，加速度測量誤差及其傳輸延遲不會使濾波結果產生較大偏差。將普通算法與輔助算法進行仿真對比，突顯出輔助算法應用于RTK技術的2個明顯優勢：1)在高動態下提高了參數估計的精度，并且在遇到周跳、野值或跟蹤到新衛星的情況下仍能夠快速收斂；2)由于模糊度浮點解精度的提高，縮小了后續模糊度整數搜索的空間，提高了搜索效率和固定成功率。

[1] 劉春卓. 基于載波相位的SINS/GPS系統研究[D]. 西安: 西北工業大學, 2005.

[2] 劉景瑞. INS輔助差分GPS組合定位中的模糊度確定的理論研究及實現[D]. 濟南: 山東科技大學, 2013.

[3] 謝鋼.GPS原理與接收機設計[M].北京：電子工業出版社,2009.

[4] Chui C K, Chen G R. 卡爾曼濾波及其實時應用(第4版)[M].北京: 清華大學出版社,2013.

[5] 許阿裴, 歸慶明, 韓松輝. 卡爾曼濾波模型誤差的影響分析[J]. 大地測量與地球動力學, 2008, 28(1): 101-104.

[6] 謝宏飛, 郝金明, 劉偉平. INS位置精度對GPS整周模糊度解算影響分析[J]. 全球定位系統, 2013, 38(1): 52-56.

[7] 鮑裕良. 基于DSP采集和處理GPS信號的系統設計[D]. 武漢: 武漢理工大學, 2005.

[8] 孫紅星. 差分GPS/INS組合定位定姿及其在MMS中的應用[D]. 武漢: 武漢大學, 2004.

[9] 劉超. GPS高精度準實時動態定位算法研究及其程序實現[D]. 西安: 長安大學, 2013.

[10] Geng Y R，Wang J L．Adaptive estimation of multiple fading factors in Kalman filter for navigation applications[J]．GPS Solutions，2008，12(4)：273-279．

[11] Feng W J，Yang S Z，Zhao F．Adaptive filtering algorithm to GPS/INS integrated system[C]//Proceedings of the 2001 International Conference on Info-Tech and Info-Net(ICII).Beijing,2001:352-356.

[12] Hide C, Moore T, Smith M．Adaptive Kalman filtering algorithms for integrating GPS and low cost INS[C]//Position Location and Navigation Symposium.IEEE Xplore, 2004：227-233．

TheResearchonAlgorithmofAmbiguityFloatSolutionofHighDynamicalRTKBasedonInertialAiding

GAO Ya-hao, ZUO Qi-yao, ZOU Zhi-qin, LI Feng, HU Wen-tao

(Beijing Institute of Automation Control Equipment，Beijing 100074，China)

As it is crucial to focus on solving the problem of fast and accurate resolution of integer ambiguity in carrier phase differential (RTK) technique, for the high dynamic application, a new method of RTK integer ambiguity float solution based on inertial information aiding is presented and a Kalman filter model based on acceleration aiding is established. The influence of acceleration error and INS information delay on the filter results are analyzed, and deep research on the dynamic performance of the algorithm by simulation is made. The simulation results show that the algorithm based on inertial aiding can obtain a more accurate integer ambiguity float solution under highly-dynamic condition compared with the non auxiliary Kalman filtering algorithm. It makes the following search space of integer solution smaller and improves the efficiency and success rate of fixing ambiguity. In the event of the cycle slip, the outlier and tracking to the new satellite signals, the algorithm also has a better performance of the resolution of the ambiguity float solution similarly. Besides, the random measurement error and information delay of INS acceleration won’t affect the performance of the algorithm greatly.

Inertial aiding; RTK; Integer ambiguity; Kalman filtering; High dynamic

2016-10-08；

2017-04-27

高亞豪(1992-)，男，碩士研究生，主要從事北斗動態差分定位方面的研究。 E-mail：heu_ziguanhui@163.com

10.19306/j.cnki.2095-8110.2017.06.010

TN967.1

A

2095-8110(2017)06-0061-07