時變干擾下欠驅動AUV水平面軌跡跟蹤的反步滑模控制
嚴浙平,楊澤文,賈鶴鳴,周佳加,王 璐
(1.哈爾濱工程大學自動化學院,哈爾濱150001;2.東北林業大學機電工程學院,哈爾濱150040)
時變干擾下欠驅動AUV水平面軌跡跟蹤的反步滑模控制
嚴浙平1,楊澤文1,賈鶴鳴2,周佳加1,王 璐1
(1.哈爾濱工程大學自動化學院,哈爾濱150001;2.東北林業大學機電工程學院,哈爾濱150040)
針對水下自主航天器AUV水平面的軌跡跟蹤問題,建立時變外界干擾條件下的運動學模型以及動力學模型,將地面誤差變量轉換為艇體坐標變量,并推導得出其誤差方程。基于Lyapunov穩定性理論研究反步滑模控制的相關算法,設計出時變干擾下的欠驅動AUV水平面軌跡跟蹤控制器,最后分析了閉環控制系統中誤差信號受到擾動時跟蹤誤差的斂散性。利用MATLAB/Simulink軟件進行仿真實驗,得出時變干擾作用下AUV對期望軌跡的跟蹤情況,經實驗驗證本文設計的反步滑模控制器能有效地跟蹤復雜軌跡,具有較強的穩定性和魯棒性。
欠驅動AUV;軌跡跟蹤;反步法;滑模控制
0 引言
水下自主航行器(Autonomous Underwater Vehicle,AUV)是實現海洋科學調查、海下煤油勘探、深水探查和海洋目標探查的重要工具。因其應用范圍廣,對AUV的深入研究已變成各國深海技術的必要課題[1-6]。研究水下自主航行器的軌跡跟蹤控制具有很強的現實意義,但在外界 (如海浪、洋流)干擾的影響下會造成軌跡跟蹤的偏離[7-8]。由于實際外界擾動具有時變性,所以在AUV軌跡跟蹤控制系統中其抗干擾性就需要著重研究。
近年來,相對于使用PID控制、自適應控制、滑模控制等一些簡單的理論,高劍等[9-11]結合幾種算法對AUV的水平面軌跡跟蹤進行控制。利用粒子群尋優算法,將非線性動力學方程偽線性化,以求解其控制器[12]。Repoulias等[13-14]對水平面航跡跟蹤的控制器設計采用反步法以及Lyapunov穩定性相關理論。李欣等[15]對AUV航行角的控制采用了基于灰度預測模糊自適應的控制算法。王一云等[16]在控制算法中加入濾波器,有效解決滑膜變結構控制中常見的顫振現象。
基于上述文獻的綜述分析,為了進一步提高AUV在時變干擾作用下控制系統的精度和抗擾性能,本文研究欠驅動AUV在水平面的運動規律,并建立其航行誤差方程。模擬AUV在實際航行中所受到的干擾問題,基于反步法、滑模控制以及Lyapunov理論設計出有效的控制器,實現對軌跡的精確跟蹤,提高軌跡跟蹤系統的穩定性和魯棒性。
1 欠驅動AUV水平面誤差方程的建立
在外界的時變擾動下,欠驅動AUV的運動學模型與動力學模型分別如式(1)、式(2)所示。
運動學模型:
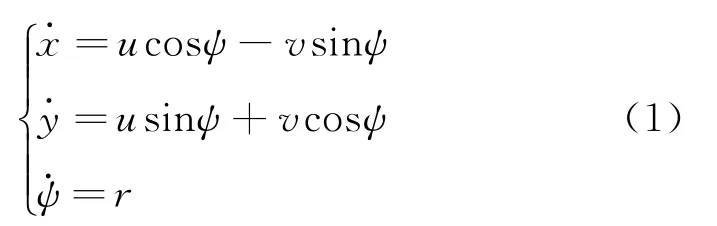
其中,x、y和ψ分別是建立在地球坐標系中AUV的位置和艏搖角,u、v、r分別代表AUV在船體坐標系中的縱向速度、橫蕩速度及艏搖角速度。
動力學模型:
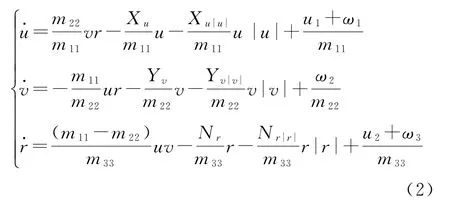
其中,X為縱向作用力,Y為橫向作用力,N為偏航力矩。m11=m-X u·,m22=m-Y v·,m33=m-N r·,X u、X u|u|、Y v、Y v|v|、N r、N r|r|為水動力參數。ω1、ω2、ω3為有界時變擾動在AUV運動系各自由度的分量。
為了方便控制器的設計,通過坐標轉換將地面誤差變量E1(t)=[x e,y e]T轉換為船體坐標變量,得到了兩個船體坐標位置誤差變量E B(t)= [e x,e y]T,并得到完全由期望軌跡表達的期望航向角在地面坐標系下定義位置和姿態誤差為:
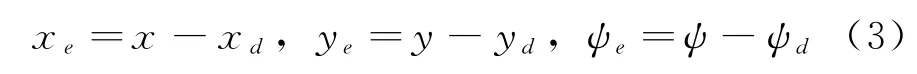
船體坐標下的位置誤差公式在坐標轉換后表示為:
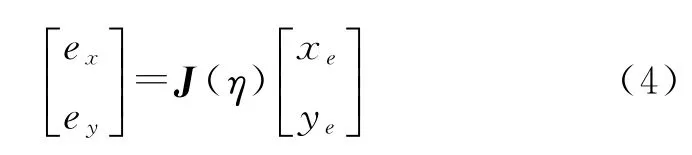
結合式(3)對式(4)求導得水平面誤差方程:
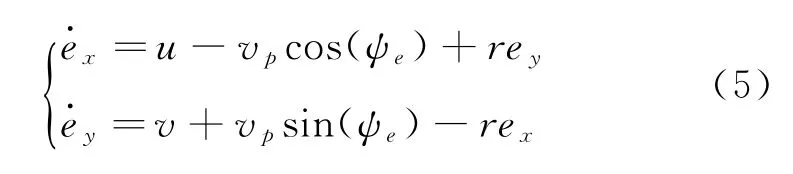
2 反步滑模控制器設計
本文中欠驅動AUV水平面軌跡跟蹤控制器基于Lyapunov相關理論和反步滑模控制理論(見圖1)。
2.1 步驟1
為了使欠驅動AUV的實際位置P(t)跟蹤期望的位置P d(t),首先構造Lyapunov函數:
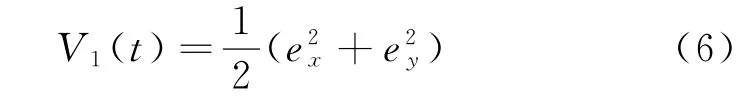
對式(6)求導,同時代入誤差方程式(5)可得:
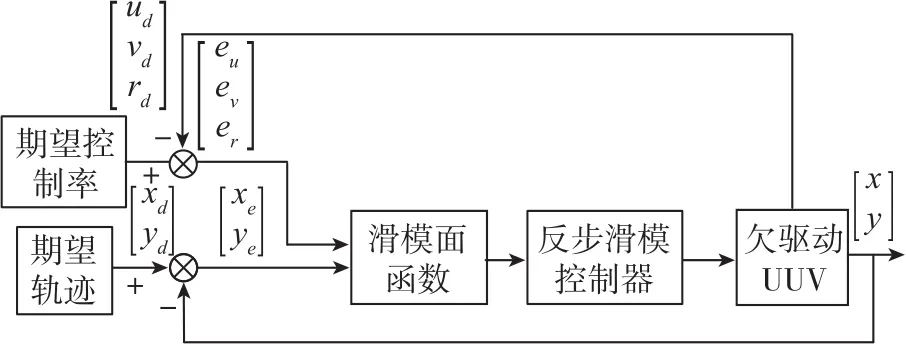
圖1 反步滑模控制系統框圖Fig.1 System block diagram of backstepping sliding mode control
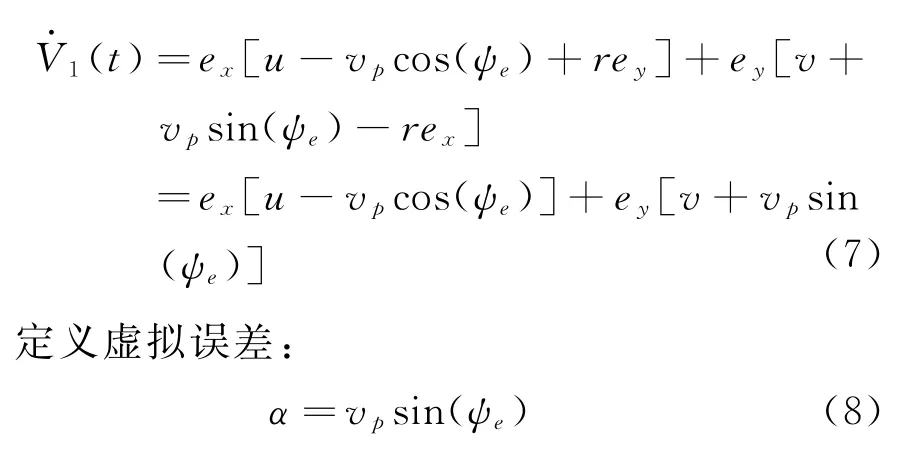
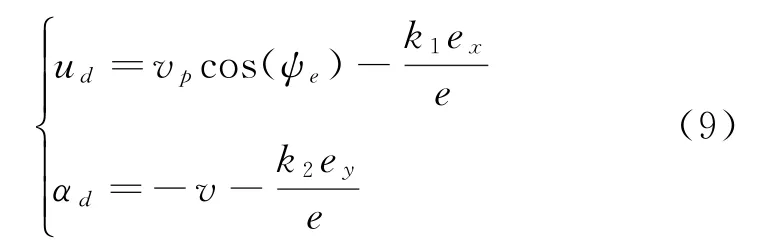
其中,k1、k2為正常數,
考慮到u d、αd不是真實的可控變量,于是定義誤差變量:
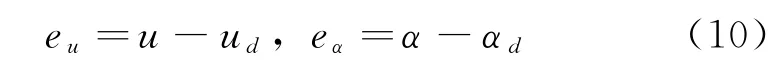
結合式(7)和式(8),得到:
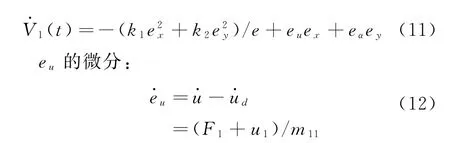
2.2 步驟2
構造Lyapunov函數并推導出實際控制力距u1:
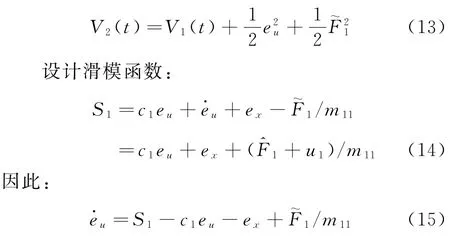
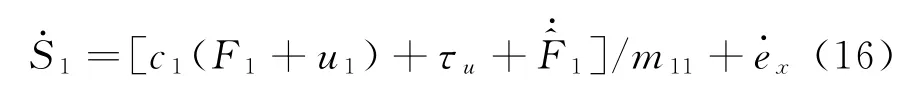
對V2(t)求導可得到:
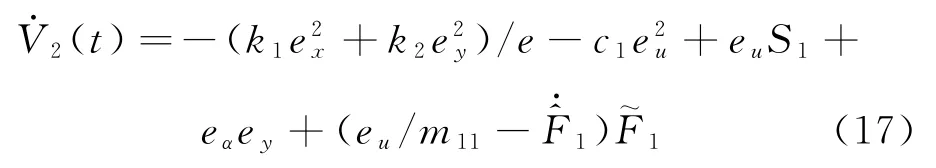
2.3 步驟3
構造Lyapunov函數:
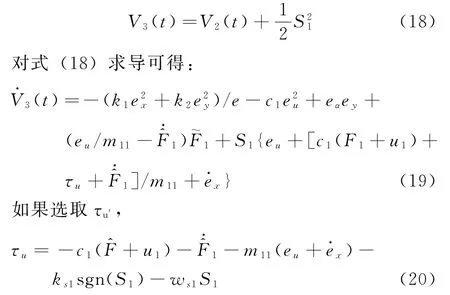
將式(19)代入式(20)可重新得到:
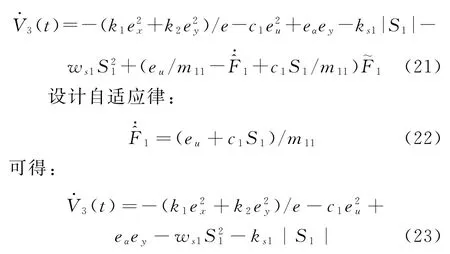
2.4 步驟4
設計控制器使eα穩定。由式(8)和式(9)可得:
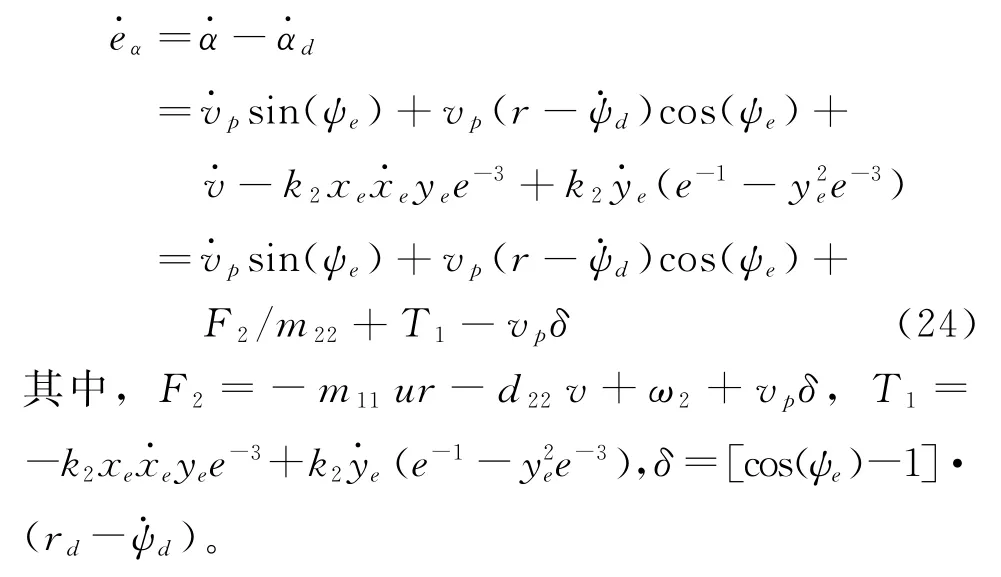
為了使V·3(t)為負,且避免設計r d時在分母中出現cos(ψe),重新定義選取r的期望值為:
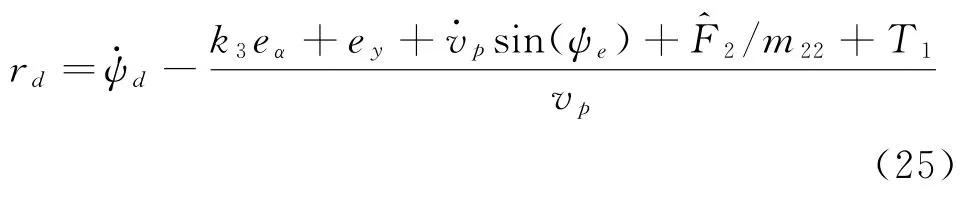
因為rd并非真實的可控變量,定義誤差變量:

可以重新得到:
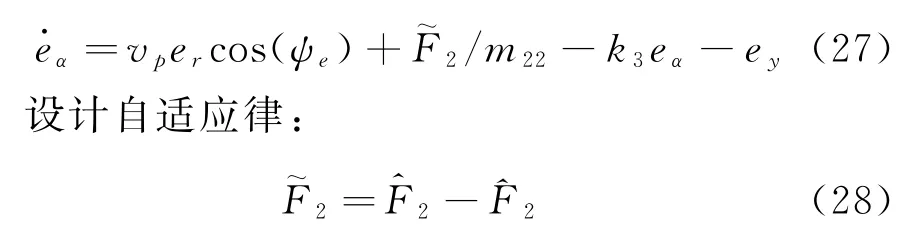
將eα視為虛擬控制輸入,構造Lyapunov函數:
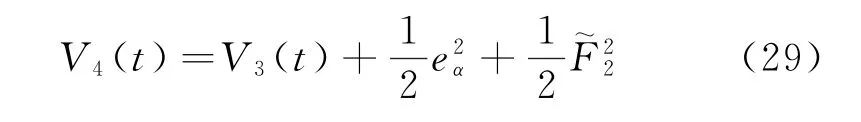
對式(29)求導可得:
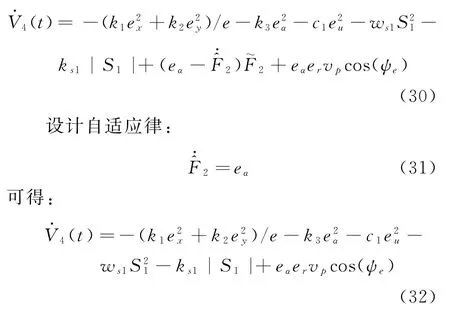
2.5 步驟5
同理,設計控制器使er穩定:
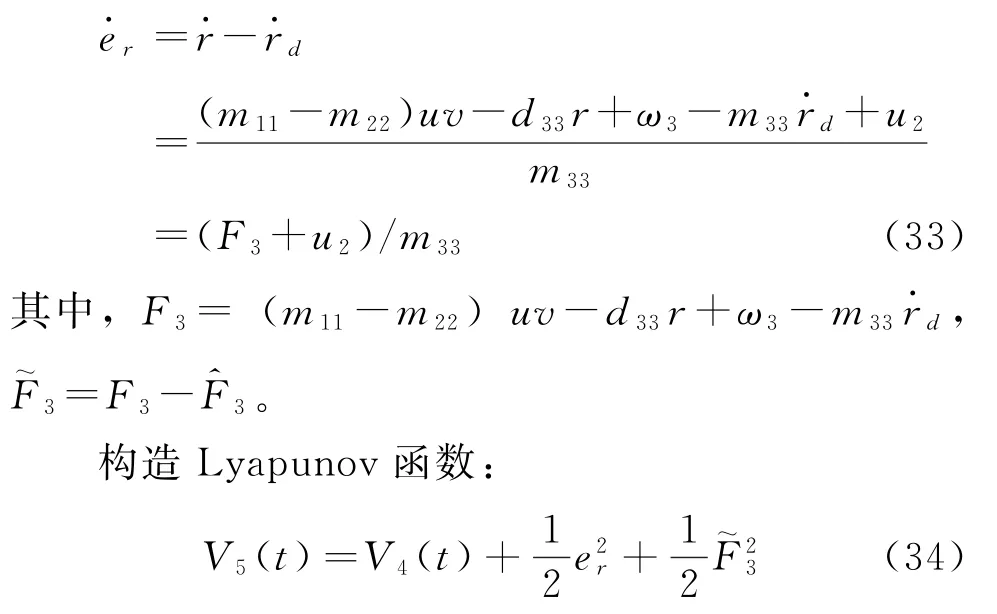
設計滑模函數:
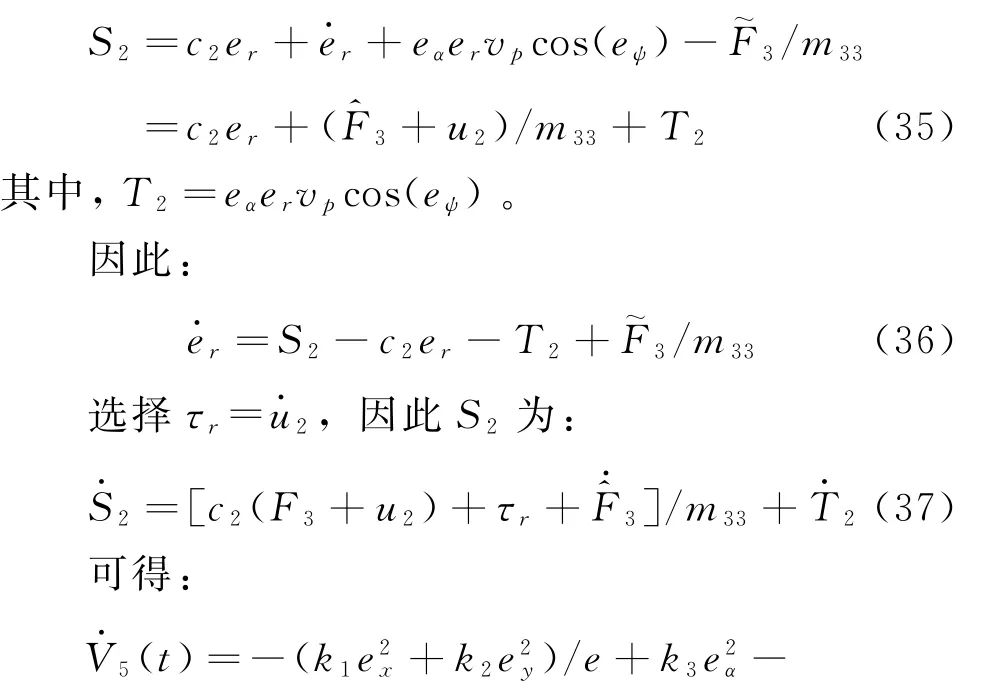
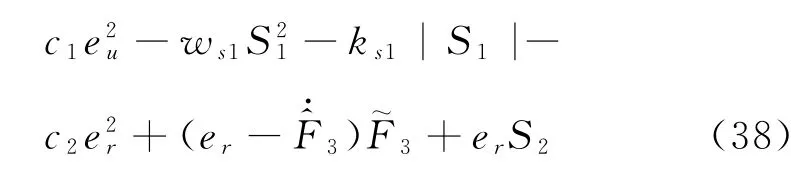
2.6 步驟6
構造Lyapunov函數
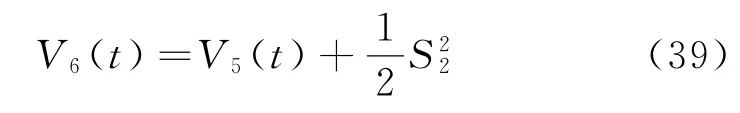
對式(39)求導可得:

最終V6(t)的微分為:
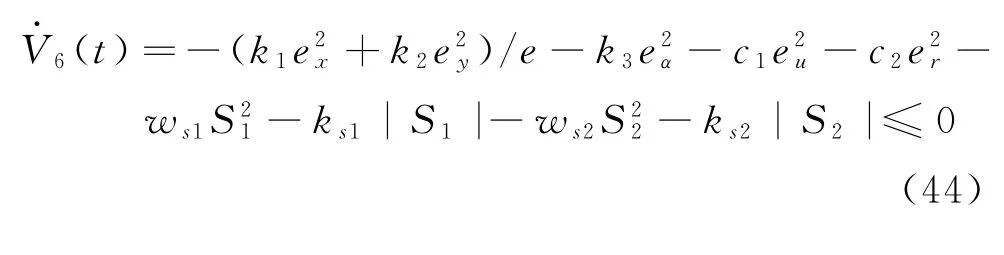
3 穩定性分析
定理:針對欠驅動無人水下航行器的運動學與動力學模型(1)-(2),如果系統采用式(20)和式 (41)的控制力和控制力矩,則閉環控制系統中的誤差信號在外界時變擾動下全局一致性是趨于穩定的,且跟蹤誤差收斂。
證明:定義
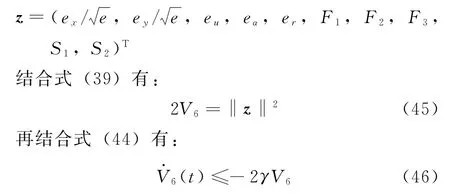
其中,γ=min{k1,k2,k3,k4,k5},由于Δ有界,根據Lasalle不變性原理,有:
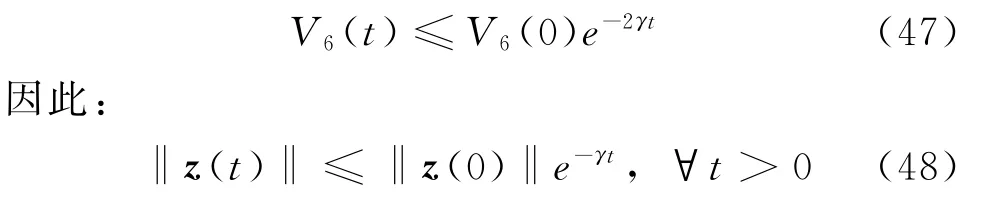
式(48)表明,跟蹤誤差z最終收斂到0,即整個AUV閉環跟蹤控制系統的全局一致性趨于穩定。
4 時變干擾下反步滑模控制仿真研究
為了驗證本文設計的反步滑模控制器是否有效,從實際工程的角度設計了一種 “5”字形的時變軌跡跟蹤曲線。所設計的欠驅動AUV水平面軌跡跟蹤控制器的MATLAB/Simulink仿真結構圖如圖2所示。
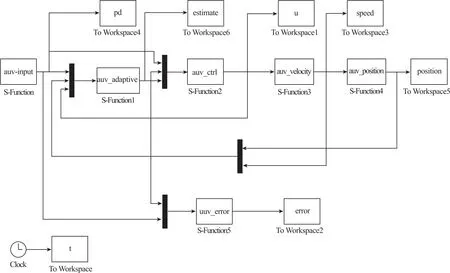
圖2 軌跡跟蹤控制器Fig.2 Controller of trajectory tracking
為了證明本文設計控制器能夠跟蹤較復雜的曲線 (即 “5”字形時變軌跡曲線,它包含了直線、半圓和斜線的曲線),以及解決當艏向角誤差ψe=±π/2時存在奇異值的情況,在設計平面跟蹤時考慮了此種情況。其中半圓部分選取軌跡為:
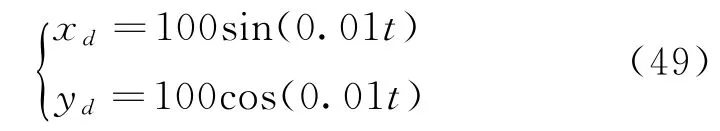
起始點為(x,y)=(0,160),即選取的初始位置誤差為(x e,y e)=(0,-10),第一個直角切換a點選取為(x,y)=(200,150),幾個軌跡直角拐點分別選取為:b:(x,y)=(200,100),c: (x,y)=(100,100),d:(x,y)=(100,50)。直線與半圓的切換點分別為e:(x,y)=(150, 50),f:(x,y)=(150,-150)。初始姿態和航速均為0,控制增益為:
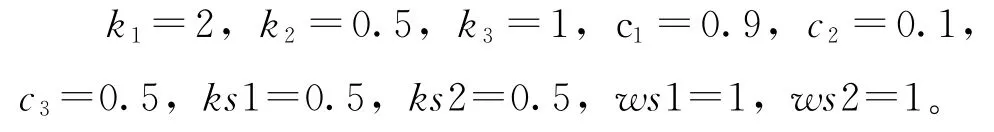
Simulink仿真實驗的結果如圖3~圖7所示。外界時變擾動為:

如圖3所示,欠驅動AUV的水平面跟蹤能完成較復雜的期望軌跡。圖4表示各項跟蹤的速度誤差與角速度誤差都足夠小,且最終趨于0,其中4個艏向角誤差ψe=±π/2也清晰可見,說明本文所提控制方法的有效性和魯棒性。圖5為欠驅動AUV線速度響應曲線和角速度響應曲線,曲線表明即使在角度突變的情況下,速度變化依然較緩,說明所提方法很好地抑制了速度突變的問題,雖然在角度突變時有較大的變化,但依然能實現對跟蹤誤差的控制。各項位置誤差變化可從圖6可以看出,曲線較快趨于0。圖7為AUV的實際控制輸入相應的變化情況。
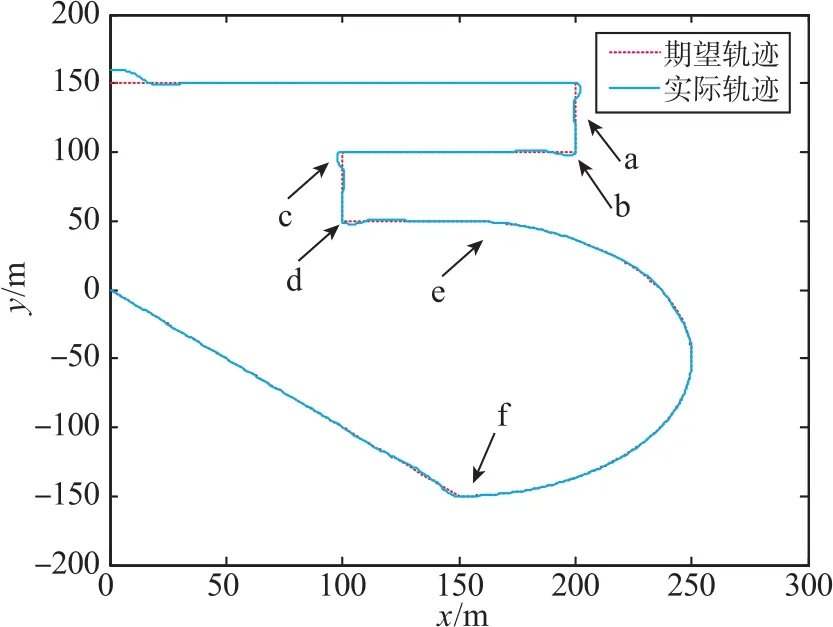
圖3 欠驅動AUV平面“5”字形軌跡跟蹤效果圖Fig.3 The underactuated AUV trajectory tracking for“5”glyph rendering
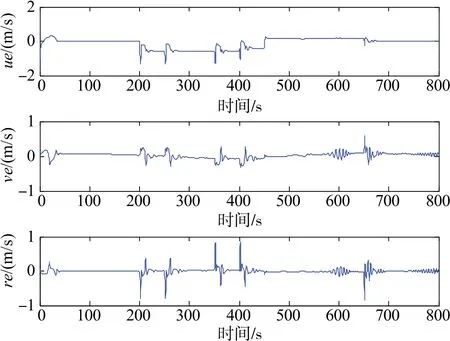
圖4 欠驅動AUV軌跡跟蹤速度誤差響應曲線Fig.4 Response curve of the underactuated AUV trajectory tracking velocity error
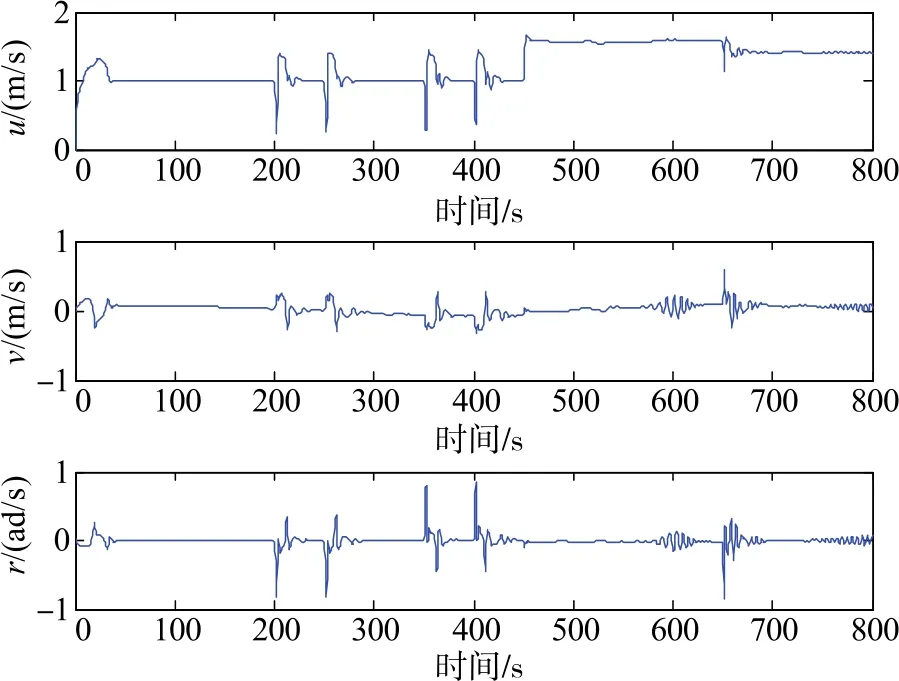
圖5 欠驅動AUV速度與角速度響應曲線Fig.5 Response curve of the underactuated AUV velocity and angular velocity
從圖3~圖7可以看出本文所設計的欠驅動AUV反步滑模軌跡跟蹤控制器能夠實現在外界時變擾動下,對時變平面軌跡的精確跟蹤。
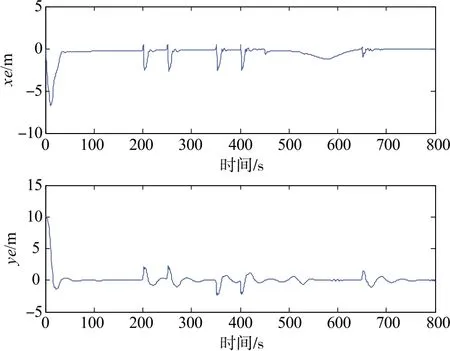
圖6 欠驅動AUV軌跡跟蹤位置誤差響應曲線Fig.6 Response curve of the underactuated AUV position error
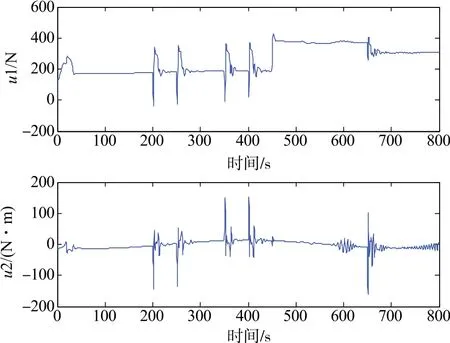
圖7 欠驅動AUV的控制輸入Fig.7 Control input of the underactuated AUV
5 結論
本文設計的基于Lyapunov理論以及反步自適應滑模算法的控制器,可以有效抑制外界時變干擾對控制系統的影響,保證了AUV水平面的軌跡跟蹤,可以滿足期望的工程要求。根據Lasalle不變性原理,驗證了誤差信號函數在外界時變擾動下全局一致漸近穩定,且跟蹤誤差收斂至0,說明在該控制律下的閉環控制系統是穩定的。通過MATLAB仿真,驗證了AUV能夠跟蹤直線、半圓和斜線的復雜曲線,各項跟蹤的速度與角速度誤差很小,并且各項位置誤差很快趨于0。因此本文設計的反步滑模控制器具有有效性、穩定性以及魯棒性,且跟蹤誤差可以較快地收斂,可以實現在時變干擾下的AUV水平面軌跡跟蹤的精確控制。
[1] 趙杰梅.離散非線性系統的預測控制方法研究[D].哈爾濱:哈爾濱工程大學,2013.
[2] 畢風陽.欠驅動自主水下航行器的非線性魯棒控制策略研究[D].哈爾濱:哈爾濱工業大學,2010: 10-20.
[3] Liu L Q,Dai Y T.3D space path planning of complex environmental underwater vehicle[C].International Joint Conference on Computational Sciences and Optimization,2009:204-209.
[4] 郝燕玲,張京娟.基于遺傳算法的AUV三維海底路徑規劃[J].中國工程科學,2003,5(11):56-60.
[5] Nathan E B.Three-dimensional route planner using A*algorithm application to autonomous underwater vehicles[D].Louisiana State University,2008: 1-15.
[6] 武善杰,鄭征,蔡開元.基于行為協同和虛擬目標相結合的無人機實時航路規劃 [J].控制理論與應用,2011,28(1):131-136.
[7] 施淑偉,嚴衛生,高劍,等.常值海流作用下的AUV水平面路徑跟蹤控制[J].兵工學報,2010 (3):375-379.
[8] 張輝.海洋環境下AUV目標跟蹤控制研究[D].哈爾濱:哈爾濱工程大學,2012.
[9] 高劍.自主式水下航行器的建模與自適應滑模控制[D].西安:西北工業大學,2004.
[10] 吳小平,馮正平,朱繼懋.模糊PID策略在AUV控制中的應用[J].艦船科學技術,2007,29(1): 95-98.
[11] 曹永輝,石秀華,許暉.水下航行器水平面運動的滑模控制[J].彈箭與制導學報,2005,25(4): 337-338.
[12] 嚴浙平,張彥超,高鵬,等.水下無人航行器水平面路徑跟蹤控制方法研究 [J].計算機測量與控制, 2011,19(12):2985-2988.
[13] Repoulias F,Papadopoulos E.Trajectory planning and tracking control design of underactuated AUVs [C].Proceedings of the 2005 IEEE International Conference on IEEE,2005:1610-1615.
[14] Repoulias F,Papadopoulos E.Planar trajectory planning and tracking control design for underactuated AUVs[J].Ocean Engineering,2007,34(11-12): 1650-1667.
[15] 李頎,石秀華,康智強.基于灰色預測的AUV水平面軌跡跟蹤控制研究 [J].西安工業大學學報, 2012,32(5):384-387.
[16] 王一云,嚴衛生,高劍,等.基于滑模變結構控制濾波的水下機器人水平面軌跡跟蹤控制 [J].計算機測量與控制,2013,21(2):382-385.
Backstepping Sliding Mode Control of the Underactuated AUV in Horizontal Plane Trajectory Tracking Under the Time-varying Disturbance
YAN Zhe-ping1,YANG Ze-wen1,JIA He-ming2,ZHOU Jia-jia1,WANG Lu1
(1.Harbin Engineering University,College of Automation,Harbin 150001,China;
2.Northeast Forestry University,College of Mechanical and Electrical Engineering,Harbin 150040,China)
According to the AUV(Autonomous Underwater Vehicle)in the horizontal plane trajectory tracking problem,based on time-varying interference the condition of the kinematics model and dynamics model is defined,transforming the ground error variables into hull coordinates,and finding out the error equation.Based on the Lyapunov theory and the algorithm of backstepping sliding mode control,horizontal underactuated AUV trajectory tracking controller in a timevarying interference is designed.Finally,the convergence or divergence of the tracking error in closed loop control system under the error signal disturbance is analyzed.Simulation studies are conducted by MATLAB/Simulink software,and the simulation experiment of AUV on the desired trajectory under time-varying interference is obtained.The experimental results show that the back-step sliding mode controller can effectively track the complex trajectory and has strong stability and robustness.
Underactuated AUV;Trajectory tracking;Backstepping method;Sliding mode control
TP273
A
2096-4080(2017)04-0001-07
2017-09-09;
2017-10-26
國家自然科學基金(51679057);黑龍江自然科學基金(E2017014)
嚴浙平 (1972-),男,工學博士,教授,研究方向為水下無人航行器的總體設計、智能控制和運動控制。E-mail:yangzewen@hrbeu.edu.cn

