基于CFD方法的低速潛航器光體及精細體模型受力計算分析

徐 暢,黃 薦,王亞興,余 超,王一偉,黃晨光

(1.中國科學院力學研究所流固耦合系統力學重點實驗室,北京100190; 2.中國科學院大學工程科學學院,北京100049; 3.中國科學院沈陽自動化研究所,沈陽110016)

基于CFD方法的低速潛航器光體及精細體模型受力計算分析

徐 暢1,2,黃 薦1,2,王亞興3,余 超1,2,王一偉1,2,黃晨光1,2

(1.中國科學院力學研究所流固耦合系統力學重點實驗室,北京100190; 2.中國科學院大學工程科學學院,北京100049; 3.中國科學院沈陽自動化研究所,沈陽110016)

利用CFD計算方法預測潛航器在額定工況下受力一直是工程上的熱點問題。通過計算給出實現預期運動所需要的各個推進器提供的靜推力,可以為相應的總體方案設計評估和推進器選型提供支撐。利用SST k-ω湍流模型結合笛卡爾網格劃分方法,對低速潛航器的光體及精細體模型進行了受力計算,并進行了網格無關性分析。分別比較了兩組模型的摩擦阻力及壓阻力計算結果,給出了模型表面壓力分布、模型周圍速度分布及流線形態,并分析了由模型外殼溝槽造成的邊界層速度分布變化。

低速潛航器;受力計算;CFD;精細體模型

0 引言

低速潛航器在海洋勘探、海洋工程、水下救助及水下勘測和檢測等方面應用廣泛,近年來得到了大量的研究發展。用于一般潛水技術不可能達到的深度或區域進行綜合考察和研究并能完成多種作業任務的水下機器人,首先要求有較高的航行和作業能力[1-2]。由于要實現全海深覆蓋,潛航器也應具備很好的垂直面深度控制與變化能力[3-5]。因而對于低速潛航器的總體方案設計評估和推進器選型而言,受力計算的方法與精度是非常重要的[6-10]。作為一種高效的阻力預報方法,計算流體力學 (CFD)方法在航行器水動力計算方面得到了廣泛應用[11-13]。深潛器相對于一般水下航行器來說,外形往往更為復雜,航行器表面存在著大量溝槽及作業設備,因此水動力計算結果與光體模型結果差異較大。如何評估精細體模型與設計中給出的光體模型計算結果之間的差異,分析其帶來的影響規律就成為了不可忽視的問題。

本文通過對典型的低速潛航器的水下航行額定工況(水平直航2kn、水平翼角90°的垂直上浮和下潛1kn、水平側移0.5kn)受力進行計算,分析了光體模型及表面帶溝槽的精細體模型的直航阻力計算結果差異。分別通過兩組模型表面壓力分布、模型周圍速度分布及溝槽附近局部速度分布云圖,討論了造成壓阻力及摩擦阻力計算結果差異的原因,并給出了不同工況下艇體表面壓力分布及流線圖。

1 數值計算方法

1.1 控制方程

本文控制方程采用雷諾平均N-S方程(RANS),即將流動變量用平均值與脈動值之和來代替,即:

其中,U=(U,V,W)代表3個方向的速度對時間的平均值,上標 “′”代表脈動值。

連續方程:

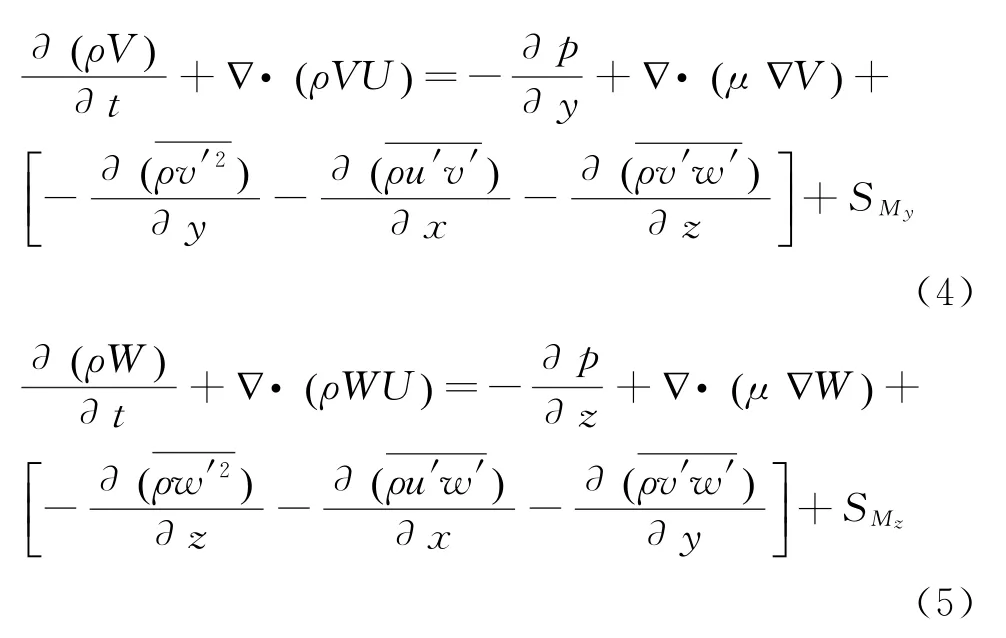
其中,x、y、z表示3個方向,ρ為流體密度, P為壓力,t為時間,μ為黏度系數,SMx、SMy、SMz是動量方程的源項。

利用Boussinesq的渦黏假定,引入渦黏性系數μt,建立Reynolds應力相對于平均速度梯度的關系,即Reynolds應力可以表述為:

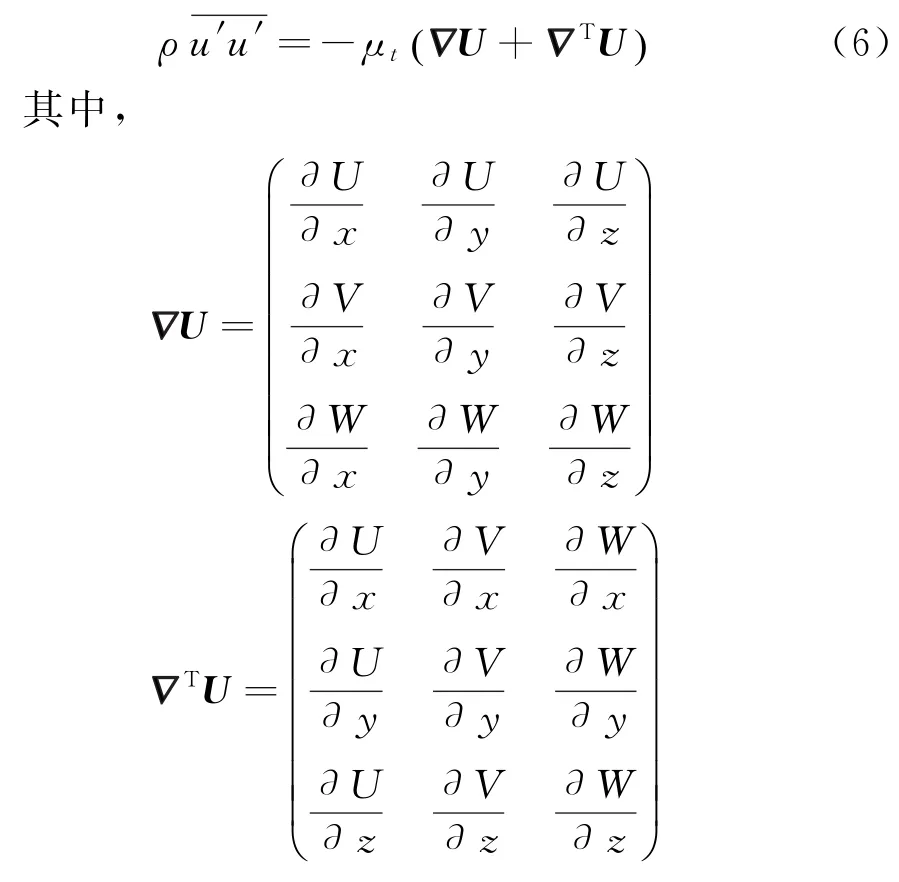
在應用過程中添加新的變量輸運方程,渦黏性系數可以表達為不同變量表達式,FLUENT軟件中應用Boussinesq渦黏假定的湍流模型有S-A模型、k-ε模型和k-ω模型,3種模型分別采用不同方法對渦黏系數進行求解[14]。本文中采用SST k-ω湍流模型。

1.2 SUBOFF標模驗證

為驗證上述方法的正確性,特采用SUBOFF全附體模型進行驗證。SUBOFF潛艇主艇體為回轉體,艇體總長為4.356m,其中進流段的長度為1.016m,平行中體的長度為2.229m,去流段長1.111m。回轉體最大直徑為0.508m,特征長度為4.261m[15]。SUBOFF標模的笛卡爾網格劃分結果如圖1所示,網格數量為192萬。在包括指揮臺圍殼和平衡尾翼等區域進行了網格加密處理。

圖1 SUBOFF標模笛卡爾網格劃分結果(網格數192萬)Fig.1 Cartesian cut-cell mesh of SUBOFF calibration model(cell number 1.92 million)

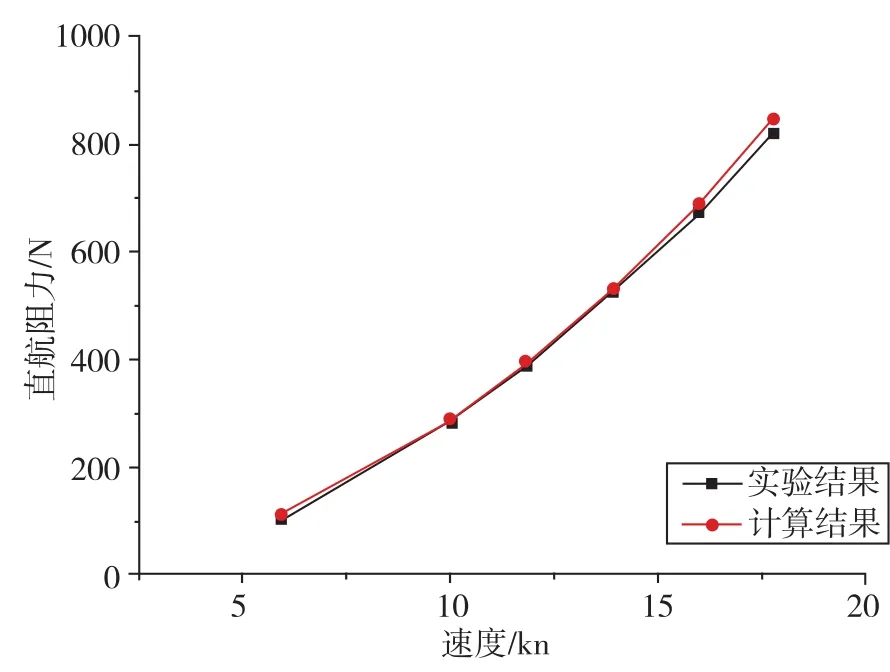
圖2 SUBOFF標模直航阻力計算結果與實驗對比Fig.2 Comparison between the simulated results and experimental data for SUBOFF calibration model

計算時采用的湍流模型是SSTk-ω模型,壓力和速度的耦合采用SIMPLE算法。采用標準方法對壓力項進行離散,速度、湍動能和湍動能擴散率等均采用2階迎風格式進行離散。計算與實驗結果比較如圖2所示。由圖2可以看出,計算結果與實驗吻合良好,驗證了數值模擬方法的準確性。

1.3 邊界條件及網格劃分

計算中定義的邊界條件包括速度入口、壓力出口以及無滑移壁面。整個三維計算域如圖3所示,計算域尺寸長為60m,寬和高都為16m。

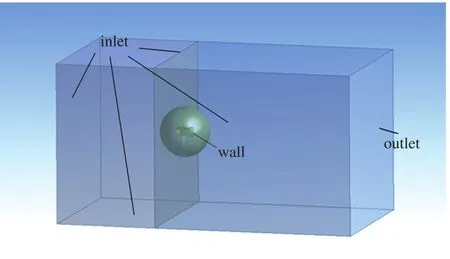
圖3 計算域與邊界條件設置Fig.3 Calculation domain and boundary conditions

計算域網格劃分時采用了笛卡爾網格方法,對尾部水翼和舵板進行了局部加密,第一層邊界層高度為3×10-4m,邊界層數15層,總網格量約為585萬。網格劃分結果如圖4所示。

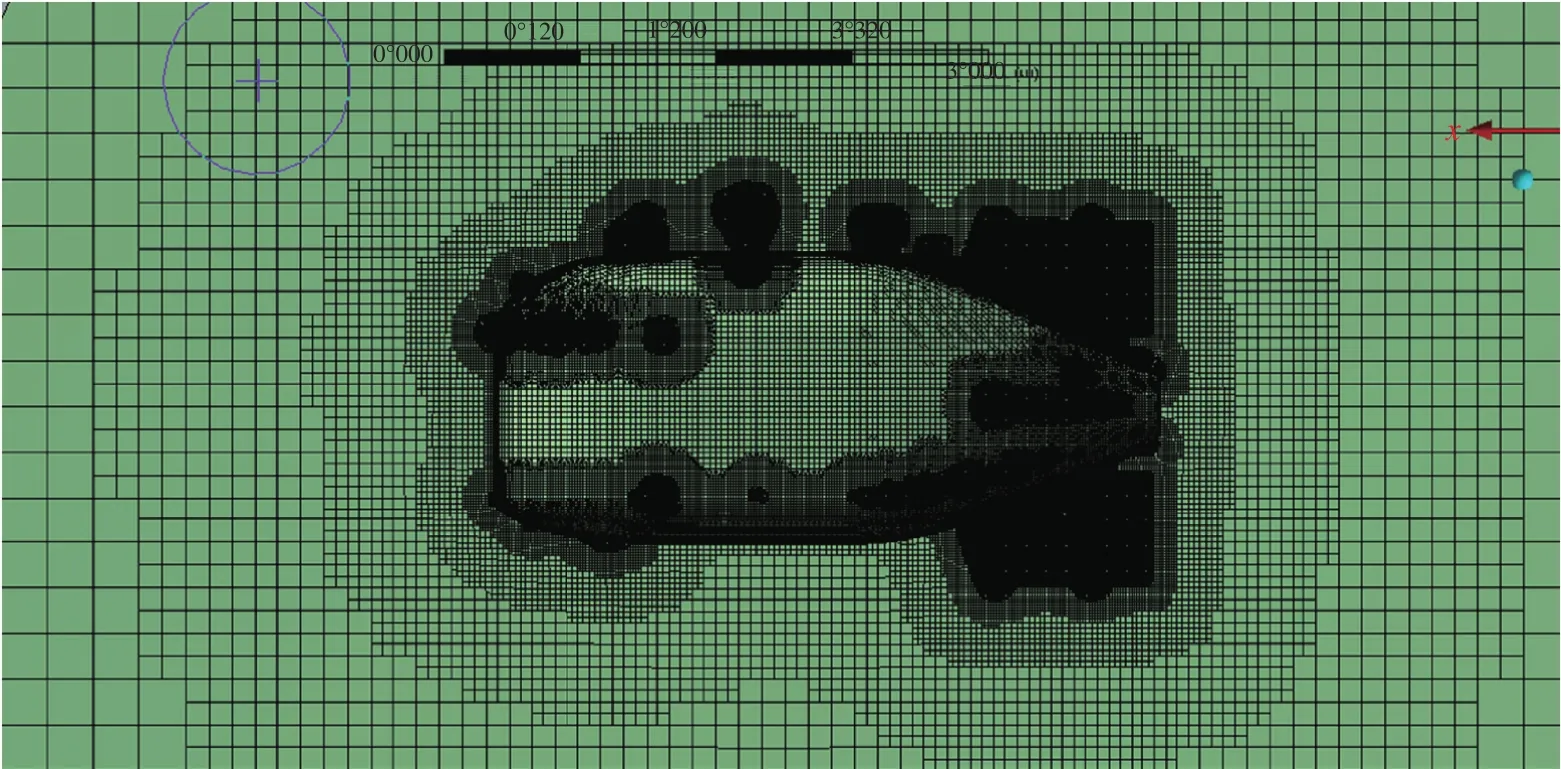
圖4 網格劃分結果(總網格數585萬)Fig.4 Cartesian cut-cell mesh around the underwater vehicle(total cell number 5.85 million)

1.4 網格無關性驗證

網格無關性驗證中包括了兩套網格,一套粗網格的網格數量為180萬,劃分時同樣采用了笛卡爾網格方法,沒有對網格進行局部加密,沒有添加邊界層。網格劃分結果如圖5所示。

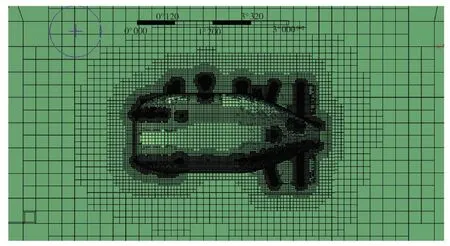
圖5 網格劃分結果(粗網格,總網格數180萬)Fig.5 Cartesian cut-cell mesh around the underwater vehicle(coarse mesh,total cell number 1.8 million)

另一套細網格的網格數量為975萬,劃分時同樣采用了笛卡爾網格方法,并對計算域中間圓形區域及尾部流場進行了加密。網格劃分結果如圖6所示。

圖6 網格劃分結果(細網格,總網格數975萬)Fig.6 Cartesian cut-cell mesh around the underwater vehicle(refined mesh,total cell number 9.75 million)

驗證計算中一共包括3套網格,網格數量分別為180萬、585萬和975萬。計算對直航0.5kn、1kn及2kn的阻力結果進行了對比,結果如表1所示。從表1中可以看出,隨著網格數量的增加,計算結果趨于收斂。由于中間網格與細網格計算結果相差很小,因此后續采用了585萬網格進行分析計算。

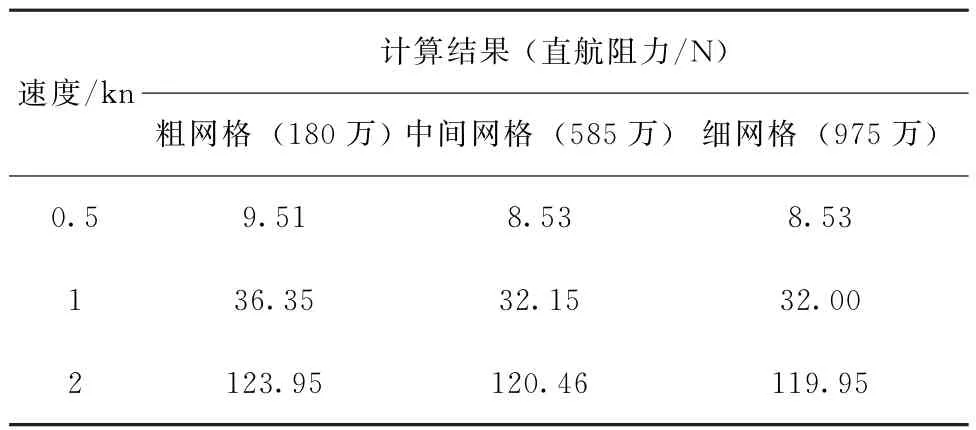
表1 3套不同網格阻力計算結果對比Tab.1 Comparison of the simulated drag of the coarse mesh,original mesh and refined mesh

2 計算結果與分析

2.1 光體模型受力計算

首先計算了水平直航2kn、水平翼角90°垂直上浮和下潛1kn、水平側移0.5kn這4個工況下航行器各方向受力和力矩情況,結果如表2所示。

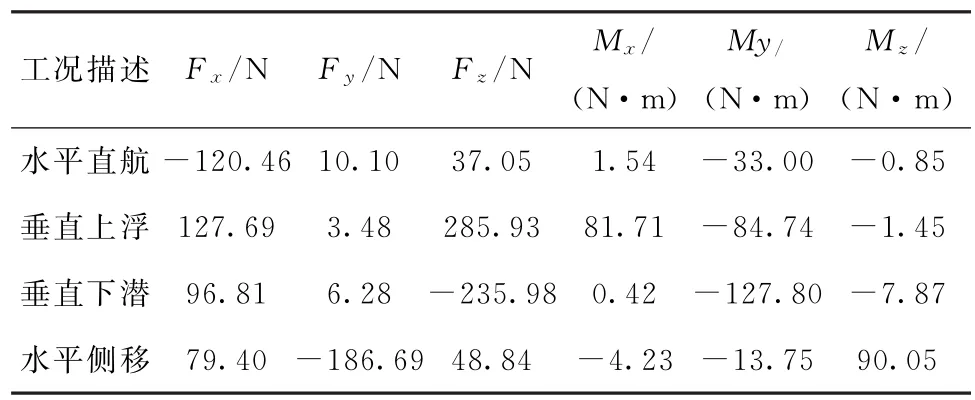
表2 直航、垂直上浮及下潛、水平側移4個工況潛航器光體模型受力和力矩結果Tab.2 Simulated results of the 4 cases for the original model (direct route,vertically float and dive,horizontally side-to-side)

2.2 精細模型受力計算

典型的精細潛航器模型表面分布了3mm溝槽及艇上配件,計算方法與之前相同。整個三維計算域的示意圖如圖7所示,計算域尺寸約為長60m、寬30m和高40m。網格劃分時對尾部水翼、舵板以及模型表面溝槽進行了局部加密,總網格量約為2657萬。網格劃分結果如圖8所示。水翼及溝槽附近局部網格劃分如圖9所示。

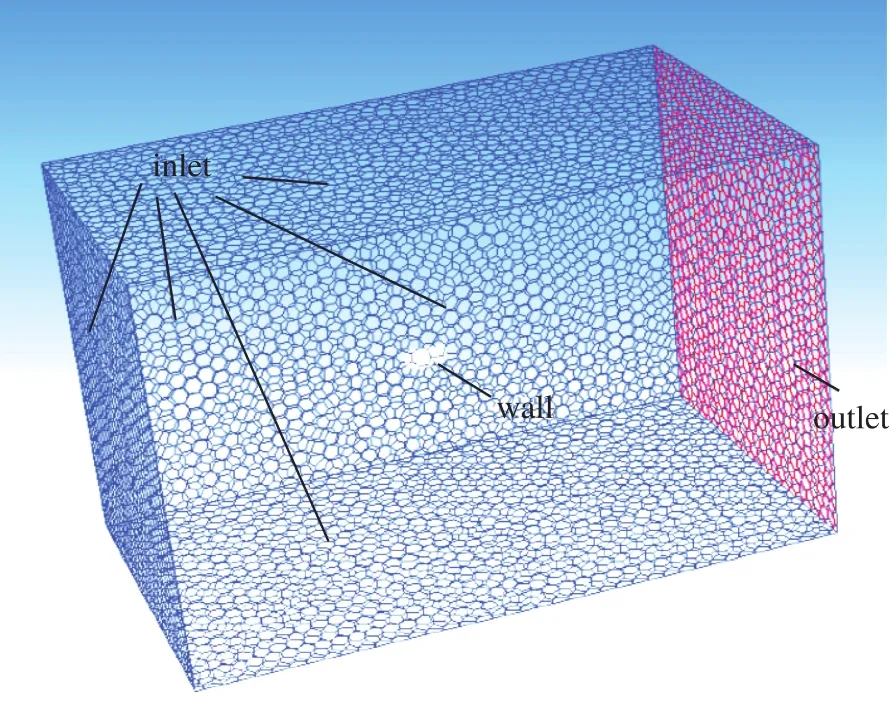
圖7 計算域與邊界條件設置Fig.7 Calculation domain and boundary conditions

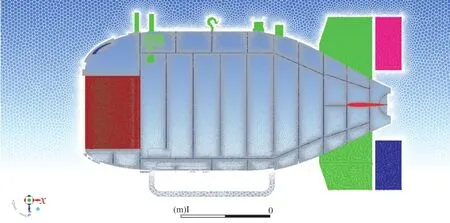
圖8 網格劃分結果(2657萬)Fig.8 Cartesian cut-cell mesh around the underwater vehicle(26.57million)

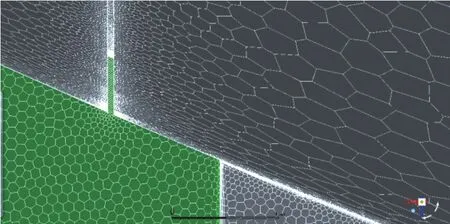
圖9 水翼及溝槽附近局部網格劃分圖Fig.9 Cartesian cut-cell mesh around the foil and grooves

同樣對水平直航2kn、水平翼角90°垂直上浮和下潛1kn、水平側移0.5kn等4個工況航行器各方向受力和力矩進行計算,結果如表3所示。

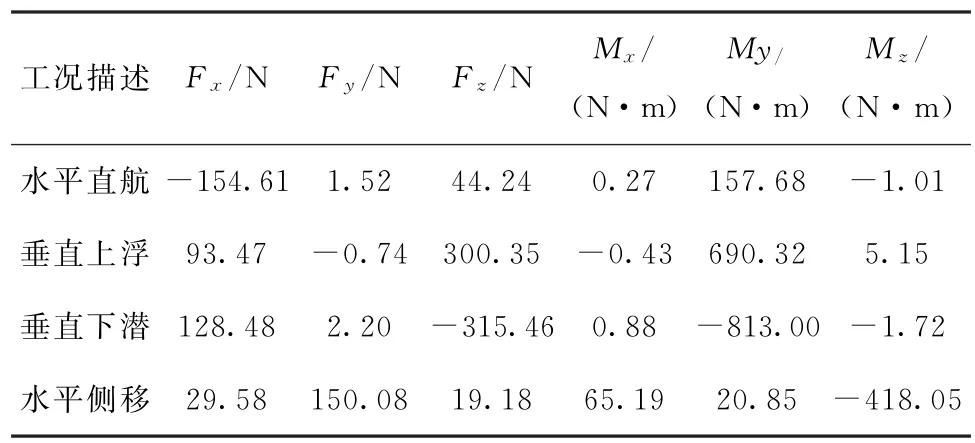
表3 直航、垂直上浮及下潛、水平側移4個工況潛航器精細體模型受力和力矩結果Tab.3 Simulated results of the 4 cases for the detailed model (direct route,vertically float and dive,horizontally side-to-side)

2.3 不同模型計算結果比較與分析

在詳細設計階段得到的精細體模型與初步設計階段得到的光體模型相比,計算所需的網格數量顯著增多,對計算資源要求較高,計算量較大。光體與精細體模型受力計算結果的差異會影響總體方案設計評估中的推力分配方案設計和推進器選型。按照潛航器所受作用力的方向分類,潛航器阻力包含了摩擦阻力和壓阻力兩種阻力成分。以水平直航阻力結果為例,表4中比較了光體及精細體模型計算結果中總阻力、摩擦阻力和壓阻力的差異。

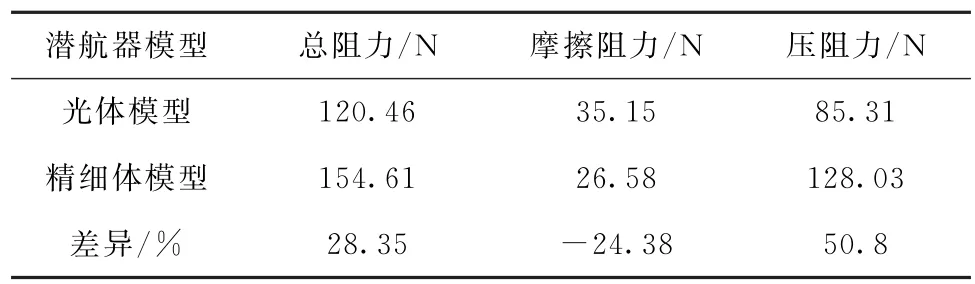
表4 直航2kn工況潛航器光體及精細體模型中總阻力、摩擦阻力和壓阻力對比Tab.4 Comparison of the total resistance,frictional resistance and pressure resistance between the original and detailed model of the underwater vehicle

由表4比較結果可以看出,精細體模型總阻力計算結果大于光體模型。其中,精細體模型摩擦阻力計算結果小于光體模型,壓阻力計算結果大于光體模型。壓阻力計算結果差異較大。圖10給出兩組計算結果中模型表面的局部壓力分布云圖,可以看出精細體模型與光體模型相比壓力分布更為復雜,模型表面溝槽處壓力變化劇烈,因而會造成整體計算結果壓阻力大幅增加。

圖11對比了潛航器光體及精細體模型周圍速度分布云圖。由圖11可以看出兩組模型計算結果中,造成速度分布差異的主要因素是由于精細體模型整體外形與光體相比更為細長,水動力性能更優,因而導致計算結果中精細體模型摩擦阻力較小。圖12中精細體模型局部溝槽附近速度分布顯示,精細體模型表面存在的溝槽并不會顯著改變邊界層厚度及其內部的速度分布,因而不會顯著影響作用在艇體表面上的切向力,即摩擦阻力。

圖10 潛航器光體及精細體模型表面局部壓力分布云圖(為方便觀測,靜壓顯示范圍-500Pa~500Pa)Fig.10 Pressure contour charts of the original and detailed model of the underwater vehicle (static pressure display range-500Pa~500Pa for observation)

圖11 潛航器光體及精細體模型周圍速度分布云圖(為方便觀測,速度顯示范圍0m/s~2m/s)Fig.11 Velocity contour charts of the original and detailed model of the underwater vehicle (velocity display range 0m/s~2m/s for observation)

圖12 潛航器光體及精細體模型 (溝槽附近)周圍局部速度分布云圖(為方便觀測,速度顯示范圍0m/s~2m/s)Fig.12 Velocity contour charts near the grooves of the original and detailed model of the underwater vehicle (velocity display range 0m/s~2m/s for observation)

水平直航2kn、水平翼角90°垂直上浮1kn、水平側移0.5kn的數值計算結果中潛航器模型表面的壓力分布及流線圖如圖13~圖15所示。圖13中航行器尾部的流線分布很平坦,圖14和圖15中流線則呈現出明顯的旋渦結構,旋渦會增加能量耗散。

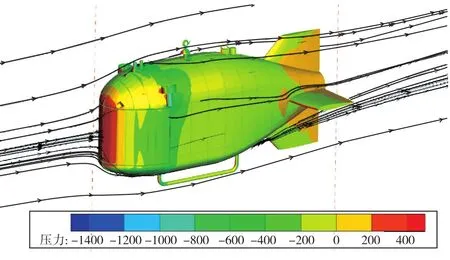
圖13 潛航器水平直航2kn模型表面的壓力分布及流線計算結果Fig.13 Pressure distribution on the underwater vehicle and velocity streamlines in the flow field(direct route 2kn)

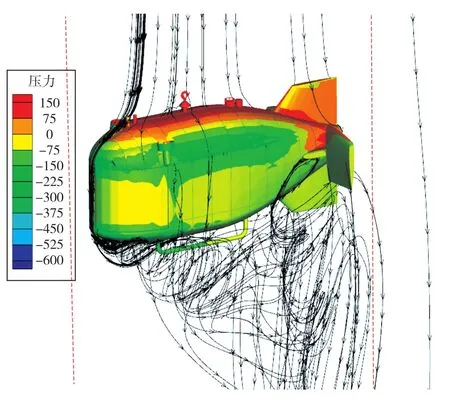
圖14 潛航器垂直(水平翼角90°)上浮1kn模型表面的壓力分布及流線計算結果Fig.14 Pressure distribution on the underwater vehicle and velocity streamlines in the flow field(vertically float 1kn)

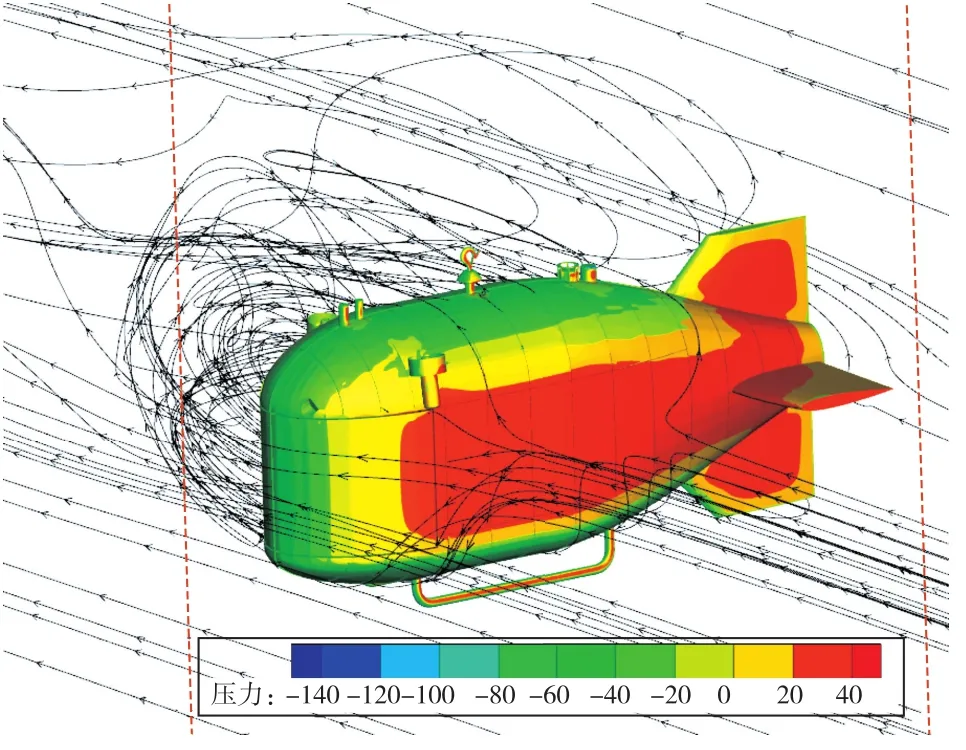
圖15 潛航器水平側移0.5kn模型表面的壓力分布及流線計算結果Fig.15 Pressure distribution on the underwater vehicle and velocity streamlines in the flow field(horizontally side-to-side 0.5kn)

3 結論

本文針對潛航器在額定工況下受力問題,利用了SSTk-ω湍流模型結合笛卡爾網格劃分方法,對低速潛航器的光體及精細體模型進行了受力計算,并進行了網格無關性分析,得到了較為一致的計算結果。

以水平直航阻力結果為例,比較了光體及精細體模型計算結果中總阻力、摩擦阻力和壓阻力的差異。精細體模型總阻力計算結果大于光體模型,精細體模型與光體模型相比壓力分布更為復雜,模型表面溝槽處壓力變化劇烈,因而會造成整體計算結果壓阻力大幅增加。精細體模型表面存在的溝槽并不會顯著改變邊界層厚度及其內部的速度分布,因而不會顯著影響作用在艇體表面上的摩擦阻力。

本文針對全海深ARV設計的關鍵力學問題開展研究,通過數值模擬手段對航行器的受力特性分析及流動規律進行研究,希望能夠支撐工程研制并推動低速潛航器水動力學基礎研究的發展。

[1] 朱克強,朱海洋,于春令,等.深海遙控潛水器多體系統非線性耦合動力特性模擬 [J].海洋工程, 2008,26(1):83-87.

[2] 范士波.深海作業型ROV水動力試驗及運動控制技術研究[D].上海:上海交通大學,2013.

[3] 封錫盛,李一平.海洋機器人30年[J].科學通報,2013(S2):2-7.

[4] 封錫盛.從有纜遙控水下機器人到自治水下機器人[J].中國工程科學,2000,2(12):29-33.

[5] 封錫盛,劉永寬.自治水下機器人研究開發的現狀和趨勢[J].高技術通訊,1999,9(9):55-59.

[6] 施生達.潛艇操縱性[M].北京:國防工業出版社,1995.

[7] Gertler M,Hagen G R.Standard equations of motion for submarine simulation[R].Dabid W Taylor Naval Ship Research and Development Center Bethesda MD,1967.

[8] Fureby C,Anderson B,Clarke D,et al.Experimental and numerical study of a generic conventional submarine at 10°yaw[J].Ocean Engineering,2016, 116:1-20.

[9] Shen Z,Wan D,Carrica P M.Dynamic overset grids in OpenFOAM with application to KCS self-propulsion and maneuvering[J].Ocean Engineering,2015,108: 287-306.

[10] Toxopeus S L,Atsavapranee P,Wolf E,et al. Collaborative CFD exercise for a submarine in a steady turn[C].31stInternational Conference on O-cean,Offshore and Arctic Engineering(OMAE), OMAE2012-83573,2012:761-772.

[11] Stern F,Yang J,Wang Z,et al.Computational ship hydrodynamics:nowadays and way forward[C]. 29thSymposium on Naval Hydrodynamics,2013, 60(1-4):3-105.

[12] Stern F,Wang Z Y,Yang J M,et al.Recent progress in CFD for naval architecture and ocean engineering[J].水動力學研究與進展B輯,2015,27(1): 1-23.

[13] Kim H,Akimoto H,Islam H.Estimation of the hydrodynamic derivatives by Ra NS simulation of planar motion mechanism test[J].Ocean Engineering, 2015,108:129-139.

[14] Pope S B.Turbulent flows[J].Turbulent Flows, 2000,12(11):806.

[15] Roddy R F.Investigation of the stability and control characteristics of several configurations of the DARPA SUBOFF model(DTRC MODEL 5470)from captive model experiments[R].Ship Hydromechanics Department Departmental Report,David Taylor Research Center,1990.

Force Calculation and Analysis of the Original and Detailed Model of Low-speed Underwater Vehicle Based on CFD Method

XU Chang1,2,HUANG Jian1,2,WANG Ya-xing3,YU Chao1,2,WANG Yi-wei1,2,HUANG Chen-guang1,2
(1.Key Laboratory for Mechanics in Fluid Solid Coupling Systems,Institute of Mechanics,Chinese Academy of Sciences,Beijing 100190,China; 2.School of Engineering Science,University of Chinese Academy of Sciences,Beijing 100049,China; 3.Shenyang Institute of Automation,Chinese Academy of Sciences,Shenyang 110016,China)

Force calculation of underwater vehicles based on CFD method is one of the mostly discussed topics within the engineering community.By calculating the required static thrust provided by the various propellers to achieve the desired motion,it is possible to support the corresponding overall design evaluation and propeller selection.In this paper,the SST k-ωturbulence model with the Cartesian cut-cell mesh method is used to calculate the force of the original and detailed model of the low speed underwater vehicle.Moreover,mesh independence study is also carried out.The results show the pressure distribution on the model.The velocity distribution around the model and the result of the streamlines in the flow field are given.Results of the velocity distribution inside the boundary layer around the vehicle caused by the grooves are analysed.

Low-speed underwater vehicle;Force calculation;CFD;Detailed model

TV698.239

A

2096-4080(2017)04-0014-08

2017-9-15;

2017-11-01

國家重點研發計劃課題(2016YFC0300802)

徐暢(1992-),女,實習研究員,主要研究方向為空泡流動。E-mail:xuchang@imech.ac.cn