對一道函數不等式證明題的探究
安徽 陳曉明
對一道函數不等式證明題的探究
安徽 陳曉明
近年來,函數不等式的證明題在高考的舞臺十分活躍,而且經常出現在壓軸題的位置.因此,對函數不等式的證明方法的探究變得很有意義.下面筆者以一道自編題為例,回顧課堂上學生精彩的探究歷程,以求掌握這類題型的通性通法,從而更好地備考!

(Ⅰ)討論f(x)的單調性;
(Ⅱ)當xgt;1時,證明:f(x)lt;g(x).
給時間讓學生充分思考,然后一起討論交流.結果學生各抒己見,給出了不同的嘗試,課堂精彩紛呈!
解法分析:
第(Ⅰ)小題比較簡單,易知f(x)在(0,+∞)上為增函數.對于第(Ⅱ)小題,學生有不同的思路,從而有不同的嘗試.
嘗試1:
運用證函數不等式最為常用的作差法.

接下來只需證F(x)lt;0.于是對F(x)求導,求F(x)max,只需F(x)maxlt;0即可.

所以求F(x)max實在太復雜,故這種嘗試以失敗告終,需另辟蹊徑!
嘗試2:





即證3x-3≤(2x-1)ex-1(xgt;1).
令h(x)=3x-3-(2x-1)ex-1(xgt;1),
則h′(x)=3-[2ex-1+(2x-1)ex-1]
=3-(2x+1)ex-1lt;0(xgt;1),
所以h(x)在(1,+∞)上為減函數,
所以h(x)lt;h(1)=-1lt;0,
即3x-3-(2x-1)ex-1lt;0,
故3x-3lt;(2x-1)ex-1.
從而原命題得證.看來“定海神針”真是管用!
嘗試3:
利用常用不等式ex≥x+1(x=0時取等號)對原不等式進行放縮.該不等式是對ex進行放縮的一個“定海神針”!滲透了轉化思想.
因為ex≥x+1(x=0時取等號),
所以ex-1≥x(x=1時取等號).①
所以g(x)=xex-1gt;x2(xgt;1).




從而原命題得證.“定海神針”再現威力!

即證3x-3≤2x2-x(xgt;1),
即證2x2-4x+3≥0(xgt;1).②
而②式易證.
這樣其實是同時利用了兩個“定海神針”進行放縮,收到了更為簡潔的效果.
啟示:以后遇到含有lnx或ex的函數不等式證明題,可嘗試兩個“定海神針”.
嘗試4:
利用最值法,證f(x)maxlt;g(x)min(*).
這種嘗試是有風險的,因為(*)式只是原命題成立的一個充分不必要條件,即原命題成立,而(*)式不一定成立.
這里不妨一試.而直接求f(x)max與g(x)min比較麻煩,甚至無最值.
為了方便,不妨對原不等式進行轉化.
要證f(x)lt;g(x)(xgt;1),





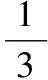

F′(x)的符號由分子決定.
令φ(x)=lnx-x+2(xgt;1),
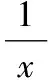
所以φ(x)在(1,+∞)上為減函數.
因為φ(3)=ln3-3+2=ln3-1gt;0,
φ(4)=ln4-4+2=ln4-2lt;0,
所以φ(3)φ(4)lt;0,
所以φ(x)在(3,4)上有唯一零點x0.


所以F(x)在(1,x0)上為增函數,在(x0,+∞)上為減函數.

因為φ(x0)=0,
所以lnx0-x0+2=0,⑥
所以lnx0=x0-2.

點評:這里利用隱零點(x0設而不求)的定義得到方程⑥,從而對lnx0進行巧妙地代換(這與前面的“定海神針”在轉化上有異曲同工之妙!),再由隱零點x0的范圍利用放縮法得證.這是高考全國卷(Ⅰ)比較喜歡考查的方法,如2012,2015年全國卷(Ⅰ)(文科)導數題都有幾乎完全相同的方法.在其它省市的高考及各級各類的聯考,模考中也更是屢見不鮮,我們可統稱為“隱零點問題”.
反思:在嘗試4中由③式轉化為④式,還有其它轉化方式嗎?如果有,該如何求解?
對于⑤式,我們還能將它轉化為哪些形式?該如何證明?
所有這些問題,讓學生課后接著探究,將課堂延伸到課外……
教學思考:
到這里,我想起葉瀾教授曾說:“課堂是向未知方向挺進的旅程,隨時都有可能發現意外的通道和美麗的因素,而不是一切都必須遵循固定路線而沒有激情行程.”
正如美國著名數學教育家波利亞所說:“一個專心的認真備課的老師能夠拿出一個有意義的但又不太復雜的題目,去幫助學生挖掘問題的各個方面,使得通過這道題,就像通過一道門戶,把學生引入一個完整的理論領域”.當然,要做到這點,首先教師對試題的本身要有深入的研究,其次,對學生的課堂參與要給予足夠的激勵和引導.把課堂還給學生,注意傾聽他們的聲音,點燃他們思維之火,讓數學課堂成為師生向往的樂園!
結束語

安徽省寧國中學)

