多角度欣賞一道高考模擬題
甘肅 李守明
多角度欣賞一道高考模擬題
甘肅 李守明
在高考復習中,不可避免地要進行多次檢測考試,怎樣才能發揮每次檢測試題的導向作用,助力學生走出“題海戰術”,提高解題能力,這就需要我們從不同的角度剖析和欣賞數學試題,發現解題規律,找出應對策略,探尋試題根源,靈活適當變式.現以蘭州市2017年3月高考診斷考試理科第20題第(2)問為例,從問題的思路及解法,溯本求源、同源變式等角度來欣賞它,僅供讀者借鑒.
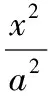
(Ⅰ)求橢圓的方程;

1 問題的思路與解法

對于問題(Ⅱ)的思路與解法,筆者從以下四個方面闡述:
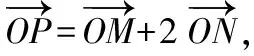
設P(x,y),M(x1,y1),N(x2,y2),
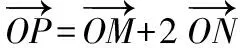
即x1=x-2x2,y1=y-2y2,

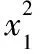
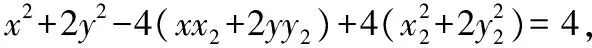

所以x2+2y2-4(xx2+2yy2)+12=0,
即x2+2y2-4[(x1+2x2)x2+2(y1+2y2)y2]+12=0,
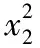
設kOM,kON分別為直線OM與ON的斜率,
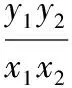
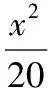
所以由橢圓的定義可知存在點F1,F2,
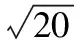
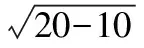
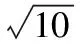
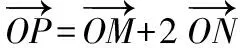
設P(x,y),M(x1,y1),N(x2,y2),
又設直線OM的方程為y=kx(k≠0),

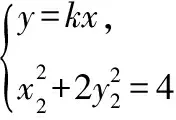

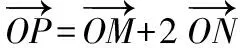
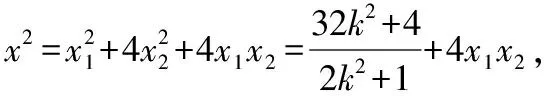
所以x2+2y2=20,后續解法同解法1.
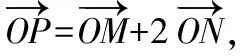
設P(x,y),M(x1,y1),N(x2,y2),
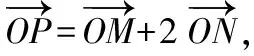

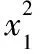
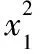
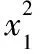
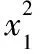
=20+4(x1x2+2y1y2),
設kOM,kON分別為直線OM與ON的斜率,
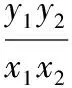
因此x1x2+2y1y2=0,
所以x2+2y2=20,后續解法同解法1.
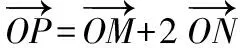

即sinαsinβ=-cosαcosβ,
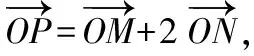
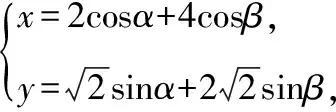

所以x2+2y2=20,后續解法同解法1.
2 溯本求源
源頭1:“我們把平面內到兩個定點F1,F2的距離的和等于常數(大于|F1F2|)的點的軌跡叫做橢圓,這兩個定點叫做橢圓的焦點”.這是人教版必修2-1對橢圓的定義,本檢測試題表面上是判斷F1,F2是否存在的問題,實際上是判斷點P的軌跡方程是否為橢圓方程的意思.隱蔽的考查了橢圓的定義,也是該題的一個特點.
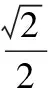
(Ⅰ)求該橢圓的方程;
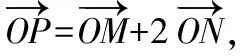
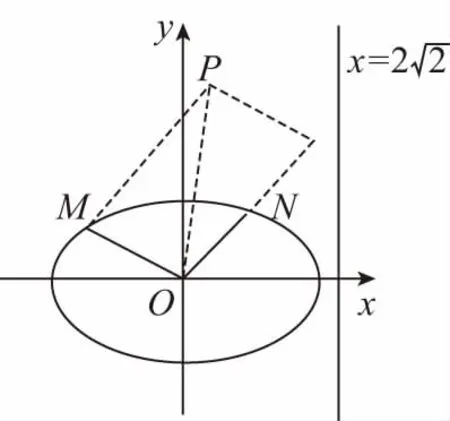
顯然,對重慶2011年高考理科試題20題的條件經過簡單的改編,就得到了本次蘭州市診斷考試的解析幾何試題.在高三復習中,教師如能夠引導學生抓住試題的特征、把握問題的本質,那么不管問題如何變化,學生都可以找到辦法,所謂變中有變,抓住不變就是這個道理,從而達到“講一題,通一類,得一法”的教學效果.
3 同源變式
在本文題目下的思路與解法3中,形式上如同把點P的坐標代入橢圓方程,最終得到了與x1x2+2y1y2有關的表達式,故只需使x1x2+2y1y2=0,則可以得到點P的軌跡方程,這是本文題目的一個重要特征,受這種特征和解法的啟示,從而有了下面的變式:

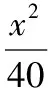
變式2:改變曲線類型.

解:設P(x,y),M(x1,y1),N(x2,y2),
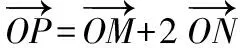

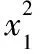
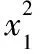
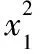

=20+4(x1x2-2y1y2),
設kOM,kON分別為直線OM與ON的斜率,
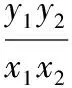
因此x1x2-2y1y2=0,所以x2-2y2=20,
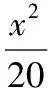
所以由雙曲線的定義可知存在點F1,F2,
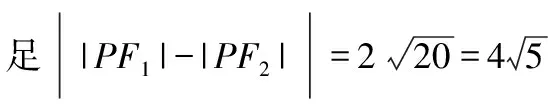



蘭州新區舟曲中學)

