Proteus在開關電阻調制跟蹤濾波器設計中的應用
田社平, 楊 玨, 方 翔, 張 峰
(1. 上海交通大學 電子信息與電氣工程學院, 上海 200240; 2. 上海辛克試驗機有限公司, 上海 201600)
Proteus在開關電阻調制跟蹤濾波器設計中的應用
田社平1, 楊 玨2, 方 翔2, 張 峰1
(1. 上海交通大學 電子信息與電氣工程學院, 上海 200240; 2. 上海辛克試驗機有限公司, 上海 201600)
中心頻率自動可調的跟蹤濾波電路是一種應用廣泛的帶通濾波電路。提出了一種基于開關與電阻串聯調制方法的跟蹤濾波器電路實現方法。開關電阻支路通過適當的電路連接方式并以一定的方式控制開關的通斷,可產生所需要的等效電阻。從能量等效的角度給出了開關電阻支路等效電阻的計算方法。討論了基于開關電阻調制的跟蹤濾波器設計方法。設計了雙二次結構的帶通跟蹤濾波器,該電路由1片四運放芯片AD713、2片模擬開關芯片DG418以及若干電阻、電容元件組成。采用Proteus對跟蹤濾波器的特性進行測試,其結果與理論分析吻合,為跟蹤濾波器的實際應用提供了可靠的依據。
開關電阻; 調制; 跟蹤濾波器; Proteus軟件
0 引 言
濾波電路應用非常廣泛,在許多測控電路中,被測信號的頻率f在很寬的頻帶內變化,要求測量電路在很窄的f±Δf頻帶內提取測量信號。在這種情況下,必須采用中心頻率自動可調的跟蹤濾波電路來提取有用的測量信號而抑制無用的干擾信號。
實現跟蹤濾波電路的方法有多種,如壓控跟蹤濾波電路[1-2]、開關電容跟蹤濾波電路[3-6]、模擬乘法器跟蹤濾波電路等[7-8]。實踐中,可以自行搭接跟蹤濾波電路,也可直接在市場中購買具有跟蹤濾波功能的集成芯片來實現相應的濾波功能[9-11]。由于具有跟蹤濾波功能的集成芯片工作模式固定等,有時不能滿足實際的功能要求。本文給出了一種基于開關電阻調制的跟蹤濾波電路設計方法,并通過電路仿真軟件Proteus測試跟蹤濾波電路的性能。
1 開關電阻調制方法
如圖1(a)所示,開關S和電阻R構成串聯支路,當S閉合時,從端口看進去的等效電阻Re為R;而當S斷開時,Re則為∞。如果開關S采用模擬電子開關,在其控制閉合、斷開的控制端施以如圖1(b)所示的周期性數字控制信號,并假設控制信號為高電平時開關閉合,為低電平時開關斷開,則可從能量等效的角度求出端口等效電阻Re。

(a) 開關電阻支路 (b) 周期性數字控制信號
圖1 開關電阻調制
假設開關電阻支路端口電壓為u,則在一個周期T內,開關電阻支路吸收的能量為
(1)
假設端口等效電阻為Re,則其在一個周期T內吸收的能量w=(u2/Re)T。由能量等效可求得開關電阻支路端口等效電阻為
Re=(T/TT)R=R/α
(2)
式中:α為周期性數字控制信號的占空比,也是開關S的通斷比。
圖2(a)所示為開關S與多個電阻連接,控制S通斷的信號占空比為α,則圖2(a)電路可等效為圖2(b)電路,其中的等效電阻分別為
R1e=R1/α,R2e=R2/α,Rke=Rk/α
(3)
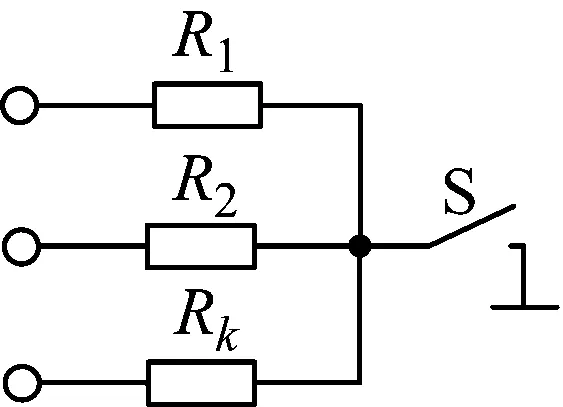
(a) (b)
圖2 開關與多個電阻連接
2 跟蹤濾波器的設計方法
圖3為采用開關電阻調制方法實現的帶通跟蹤濾波器電路,它通過對雙二次環濾波電路中的部分電阻進行開關調制來達到帶通中心頻率可調的目的[12]。

圖3 基于開關電阻調制的帶通跟蹤濾波器
假設控制端C的信號周期為T,占空比為α,則在一個周期內,開關S1、S2閉合時間TT=αT,電阻R1受到開關S1的調制,R2~R4受到開關S2的調制,其等效電阻分別為
Rie=Ri/α=(T/TT)Ri,i=1,2,3,4
(4)
假設圖3電路的作用是將頻率為f以外的信號濾除,亦即帶通的中心頻率為f。為使得在一個周期內等效電阻的等效值盡量恒定,可取開關控制信號的頻率為頻率f的n倍(n為一較大的整數)。此時,式(4)可改寫為:
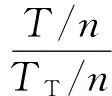
(5)
式中:ω=2πf,為帶通電路的中心角頻率;fT=1/TT,稱為全導通頻率;ωT=2πfT,稱為全導通角頻率,為固定值。顯然,當控制信號頻率為fT時,Rie即為Ri。
由上面分析,可得圖3電路的輸入輸出特性為

(6)
由式(6)可知,圖3電路具有帶通特性,且中心頻率為
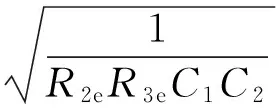
(7)
品質因數為

(8)
中心頻率處的放大倍數為

(9)


(10)
由式(10)可知,圖3電路的帶通中心頻率處的放大倍數A與品質因素Q不隨ω發生變化,為固定值,因此,圖3電路具有帶通跟蹤濾波的功能。
3 基于Proteus的跟蹤濾波性能測試
為驗證跟蹤濾波器的性能,采用電路仿真軟件Proteus進行測試[13-14]。在Proteus環境中設計如圖4所示的帶通跟蹤濾波器,電路采用雙二次結構。該電路由1片四運放芯片AD713、2片模擬開關芯片DG418以及若干電阻、電容元件組成。圖中參數:ωT=666.67 rad/s,TT=9.42 ms,品質因數Q=10,中心頻率處的放大倍數A=1。
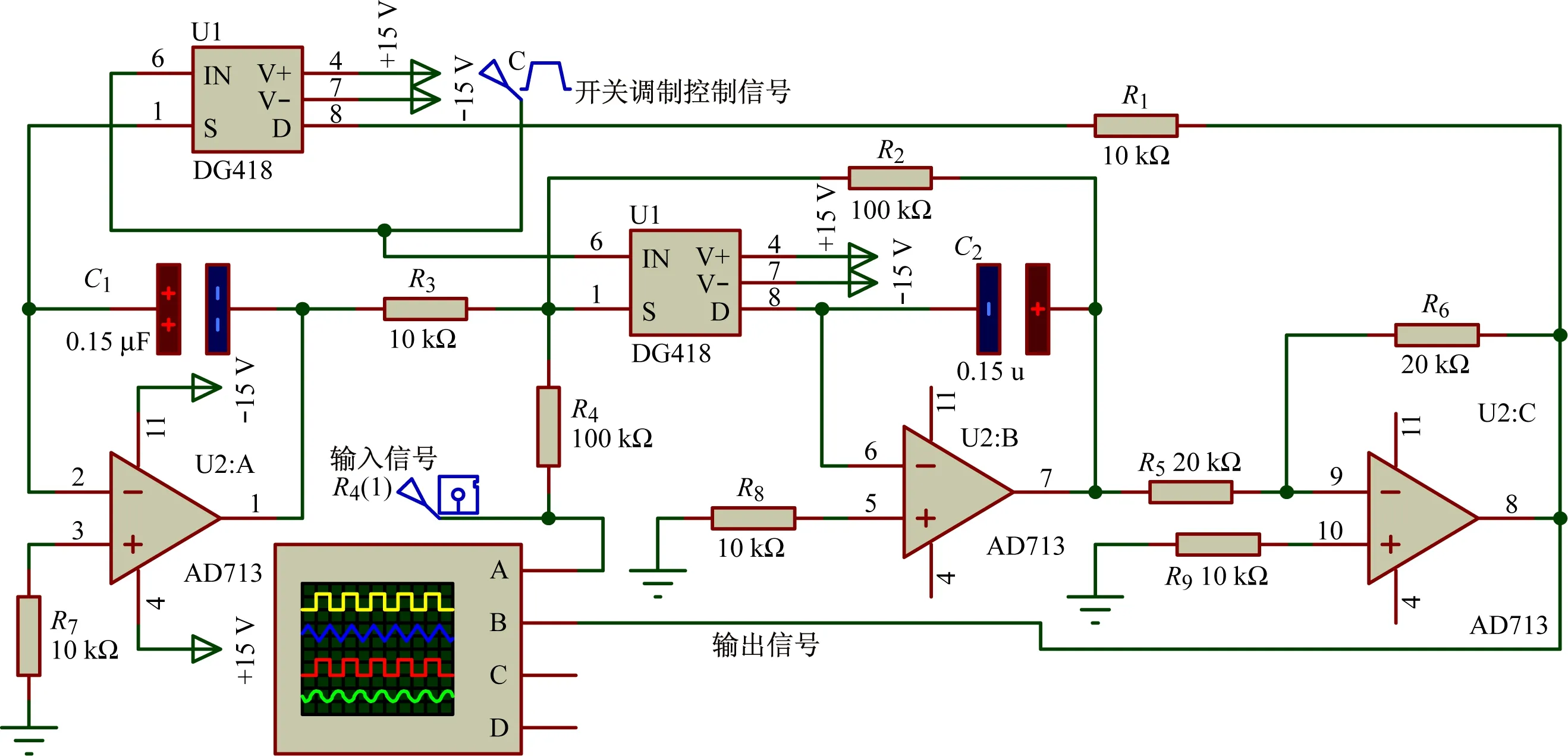
圖4 帶通跟蹤濾波器實例
3.1 頻率特性測試
取電路的帶通中心頻率f=40 Hz,倍頻數n=100。在開關調制控制信號C端輸入頻率為4 kHz的矩形波開關控制信號,其脈寬為TT/n=94.2 μs。在輸入信號端施加不同頻率的正弦波,測量輸出信號與輸入信號的幅值比和相位差,繪制的頻率特性曲線見圖5。由圖可見,電路具有良好的帶通特性。
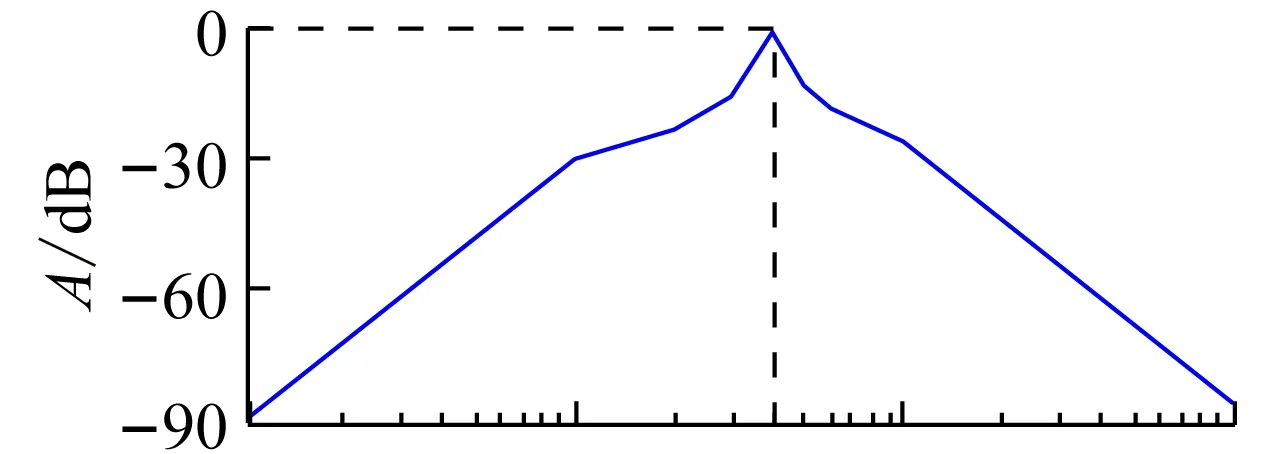

圖5 帶通中心頻率f=40 Hz時的頻率特性
3.2 倍頻數n的選擇
倍頻數n的等效應合理選擇,n太小,由于開關通斷的切換導致波形光滑性差,出現鋸齒波形;n太大,由于開關控制波形的脈寬與n呈反比,導致脈寬太窄,可能出現受模擬開關的響應時間限制而出現開關無法動作的情形。對圖5電路,取電路的帶通中心頻率f=40 Hz,令n=20,則有TT/n=4.71 ms,在輸入端施加振幅為10 V,頻率為40 Hz的正弦波,其輸出波形如圖6(a)所示,可以明顯看出波形中的鋸齒成分;而令n=100時的輸出波形如圖6(b)所示,可以看出波形的光滑性得到較明顯改善。在Proteus中通過改變n觀察輸出波形,發現當n=100左右時波形的光滑性和模擬開關的響應性能都比較滿意。本文將該電路應用于轉子動平衡測量系統中,取n=100得到了滿意的效果[15]。
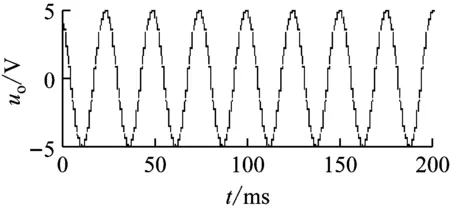
(a)n=20
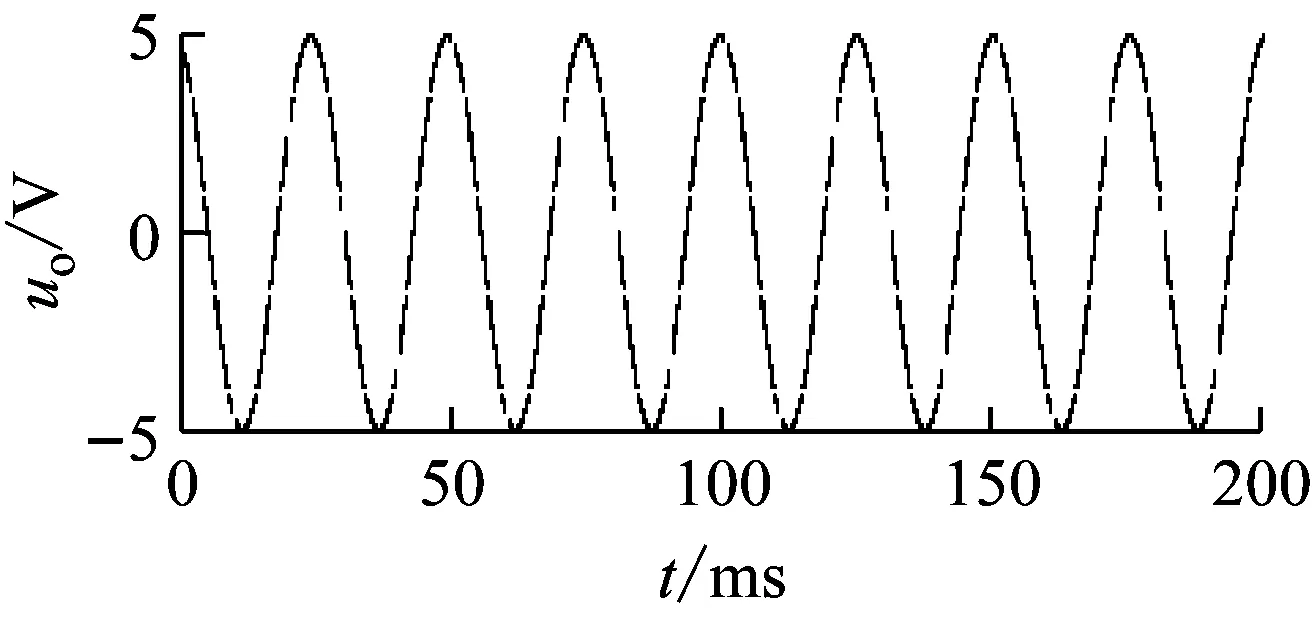
(b)n=100
圖6 倍頻數n的選擇
3.3 濾波性能測試
帶通濾波的目的是去除干擾信號,提取頻率為濾波器中心頻率的有用正弦信號。采用Proteus進行濾波性能測試的方法如下:在圖4電路中的輸入信號端[R4(1)]施加混有隨機干擾的正弦波信號(通過合成理想正弦信號和正態分布噪聲信號而得到的數據文件),在輸出信號端觀察波形。
圖7給出仿真測試結果,其中輸入信號
ui=50sin(2π×40t)+n(t)
n(t)為均值為零,標準差為50的正態分布噪聲,單位為mV,亦即輸入信號的信噪比為0 dB。uo為輸出信號。由圖可以看出,由于電路的品質因數Q=10,為一較大值,故電路基本上可以完全濾除干擾信號,uo的振幅略低于50 mV,說明電路具有良好的帶通濾波性能。

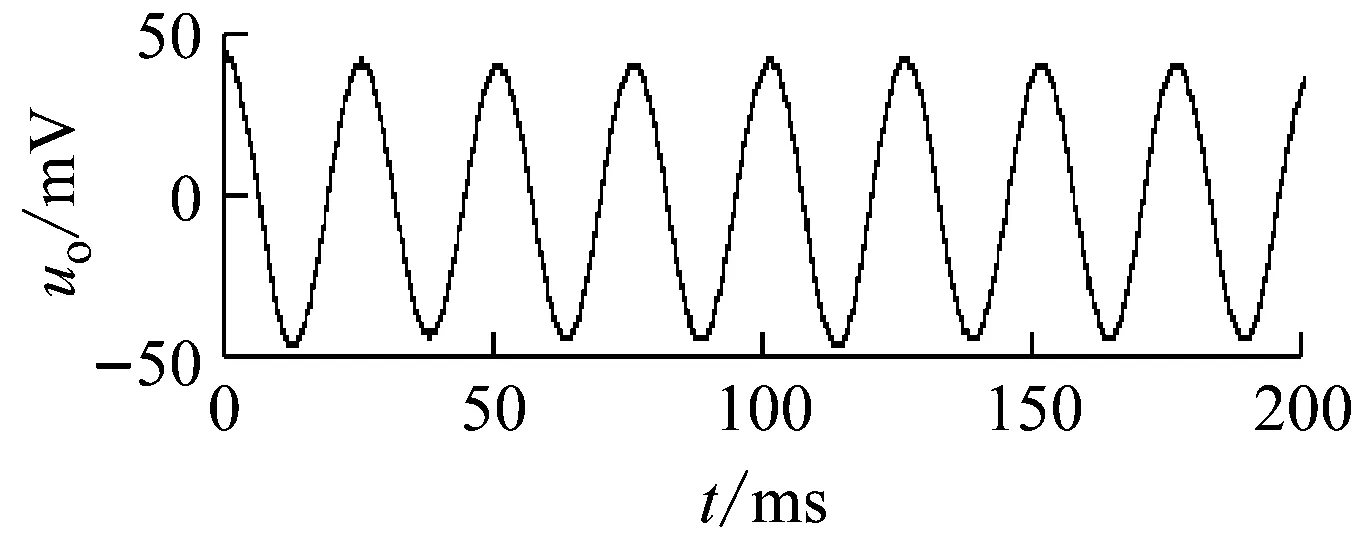
圖7 濾波性能測試
4 結 語
提出了一種基于開關電阻調制的帶通跟蹤濾波器的設計與實現方法,并采用Proteus軟件對電路性能進行了仿真測算,極大地提高設計分析效率,為電路的實際應用奠定了堅實的基礎。采用Proteus進行電路性能測試的優點在于電路設計過程簡單,試驗測量方便,而且仿真測試結果與電路實際應用結果也十分吻合。
[1] 張國雄. 測控電路[M]. 4版,北京:機械工業出版社, 2011.
[2] 李曉鵬,徐 靜, 李 矩, 等. 壓控跟蹤濾波器原理與實現方法[J]. 現代制造工程,2006(6):114-115.
[3] 彭永棒,孫奉婁,藍加平,等. 基于CPLD 的開關電容組式跟蹤濾波器設計與實現[J]. 微型機與應用,2013,32(3):19-22.
[4] 陳懷超, 叢培田. 基于開關電容的自動跟蹤濾波器的設計及研究[J]. 儀表技術與傳感器,2003(10):38-39.
[5] 林 濤. 開關電容跟蹤濾波器的研究[J]. 西安公路學院學報,1995,15(1):97-99.
[6] 陳照章. 跟蹤濾波器的設計及其應用[J]. 儀器儀表學報,2001,22(3):244-246.
[7] 叢培田,華 雷,田明德,等. 模擬乘法器式自動跟蹤濾波器設計與研究[J].沈陽工業學院學報,1993,12(4):25-29.
[8] 陶利民, 肖定邦, 溫熙森. 用于動平衡測試的MDAC窄帶跟蹤濾波器[J]. 國防科技大學學報,2006,28(2):102-105.
[9] 于巍巍, 顏德田, 楊 樾. 基于MAX260 的自動跟蹤濾波器的工程設計與應用[J]. 現代電子技術,2008,16(5):76-78.
[10] 李旭濤,丁國清. 基于MAX268的自動跟蹤濾波器的研究及應用[J]. 電測與儀表,2006,43(3):62-64.
[11] 張建峽, 徐 云, 張凱洪, 等. 自適應信號分解實驗裝置[J]. 實驗技術與管理,2011,28(3):66-68.
[12] 田社平,秦 琳. 基于脈寬調制的雙二次環跟蹤帶通積分電路及其控制方法[P]. 中國專利:ZL2010105011555.3,2014-05-21.
[13] 閆俊榮,崔 霞,張彩榮. 濾波器的頻率特性仿真實驗研究[J]. 實驗技術與管理,2012,29(1):86-88.
[14] 劉德全. Proteus 8-電子線路設計與仿真[M]. 北京:清華大學出版社,2014.
[15] 俞水鋒,楊 玨,林曉娟,等. 基于數字陷波濾波器的轉子不平衡量測量[J]. 計量技術,2011(10):15-18.
ApplicationofProteusinModulationofSwitchingResistorsinTrackingFilterDesign
TIANSheping1,YANGJue2,FANGXiang2,ZHANGFeng1
(1. School of Electronic, Information and Electrical Engineering, Shanghai JiaoTong University, Shanghai 200240, China; 2. Shanghai Schiak Testing Machinery Co., Ltd., Shanghai 201600, China)
The tracking filter with automatically adjustable center frequency is a widely used band-pass filter circuit. A realization method of the tracking filter circuitis is proposed based on modulation of switching resistors. The desired equivalent resistance can be obtained through appropriate circuitry and control of switch mode. The equivalent resistance can be computed through energy equivalence theory. The design of tracking filter based on modulated switching resistors is discussed. A tracking filter with biquadratic structure is designed. The filter is composed of a four op-amp chip (AD713), two single-pole/single-throw analog switch chips (DG418) and some resistors and capacitors. Proteus software is applied to measure the characteristics of the tracking filter, and the simulation results coincide with those of theoretical analysis.The method provides a reliable basis for the application of the tracking filter.
switching resistor; modulation; tracking filter; Proteus software

TN 713.5
A
1006-7167(2017)11-0036-04
2017-01-20
上海交通大學教學發展中心教學發展基金項目(CTLD16A001)
田社平(1967-),男,湖北仙桃人,副教授,現主要從事電路理論和動態測試技術等的教學和科研工作。
Tel.:18964576620; E-mail:sptian@sjtu.edu.cn

